Mesh Parameterization Theory and Practice NonPlanar Domains Limitations

Mesh Parameterization: Theory and Practice Non-Planar Domains

Limitations of planar domains • so far … parameter domain = topological disk – one connected component – one boundary • parameterization bijective ⇒ surface = topological disk • what about other surfaces? Mesh Parameterization: Theory and Practice Non-Planar Domains

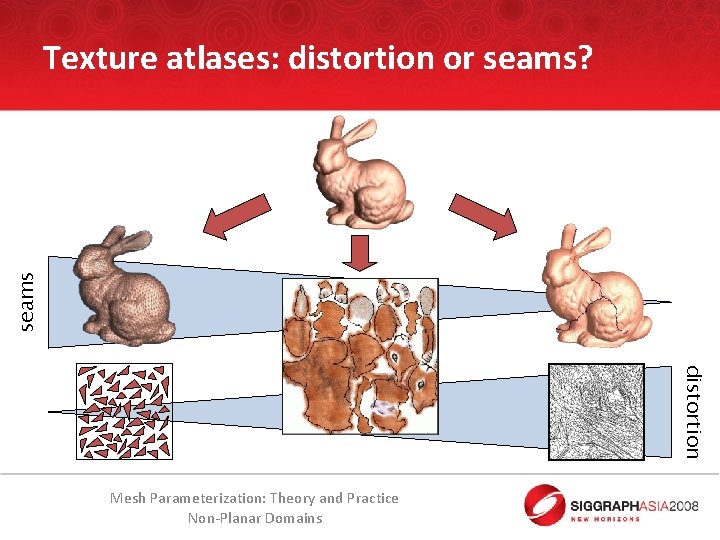
seams Texture atlases: distortion or seams? distortion Mesh Parameterization: Theory and Practice Non-Planar Domains

Beyond planar domains • alternative: adapt the parameter domain – same topology as the mesh • base complexes – simplified triangle mesh • spherical domains – limited to genus-zero meshes • polycubes – quadrilateral domain elements Mesh Parameterization: Theory and Practice Non-Planar Domains

Generating base complexes • surface triangulation of seed points • successive simplification [Lee et al. 1998] Mesh Parameterization: Theory and Practice Non-Planar Domains [Eck et al. 1995]

Computing the parameterization • initial parameterization – parameter points for mesh vertices – inherit correspondences during simplification – piecewise linear map per mesh triangle • optimization – Loop smoothing – global minimization of distortion with transition functions [Khodakovsky et al. 2003] Mesh Parameterization: Theory and Practice Non-Planar Domains

Applications and limitations • applications – – remeshing compression surface fitting morphing • limitations – not good for texture mapping – where to store the color data? Mesh Parameterization: Theory and Practice Non-Planar Domains

Spherical parameterizations • projected Gauss-Seidel iterations [Kobbelt et al. 1999] – project all points onto sphere – compute barycentric average – reproject onto sphere • problems – does not guarantee bijectivity – diverges close to solution [Saba et al. 2005] • solution – spherical barycentric coordinates[Gotsman et al. 2003] Mesh Parameterization: Theory and Practice Non-Planar Domains

Alternatives • successive simplification [Praun & Hoppe 2003] Mesh Parameterization: Theory and Practice Non-Planar Domains [Shapiro & Tal 1998]

Applications and limitations • applications – remeshing [Praun & Hoppe 2003] – compression, morphing, … • cube maps – texture mapping • limitations – only spherical meshes Mesh Parameterization: Theory and Practice Non-Planar Domains

Polycubes • polycubes as parameter domains – – [Tarini et al. 2004] square domain elements matching topology similar coarse shape not too many elements • construction – interactively [Tarini et al. 2004] Po·ly·cube: n. (Geom. ) A solid composed of multiple unit – automatic [Lin et al. 2008] cubes attached face to face Mesh Parameterization: Theory and Practice Non-Planar Domains

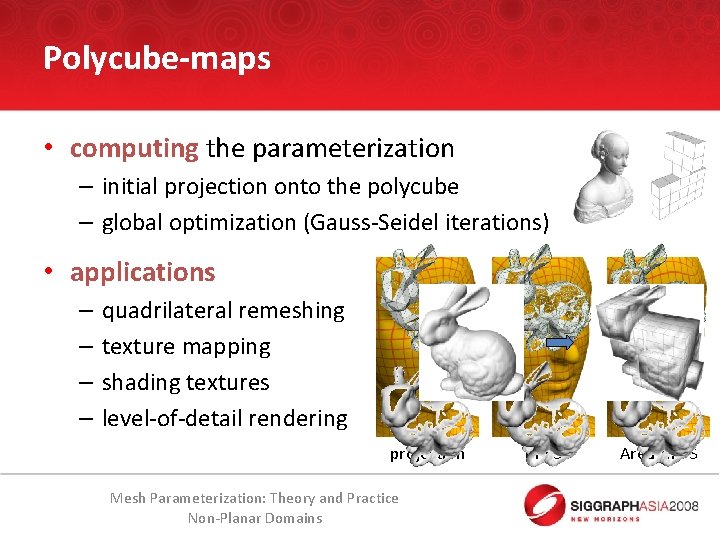
Polycube-maps • computing the parameterization – initial projection onto the polycube – global optimization (Gauss-Seidel iterations) • applications – – quadrilateral remeshing texture mapping shading textures level-of-detail rendering projection Mesh Parameterization: Theory and Practice Non-Planar Domains MIPS Area-MIPS

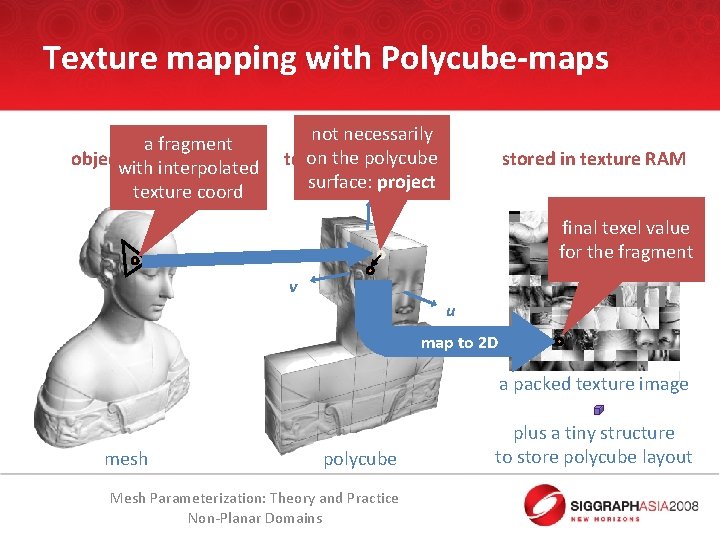
Texture mapping with Polycube-maps a fragment objectwith space interpolated texture coord not necessarily on thespace polycube texture (3 D!) surface: project stored in texture RAM w final texel value for the fragment v u map to 2 D a packed texture image mesh polycube Mesh Parameterization: Theory and Practice Non-Planar Domains plus a tiny structure to store polycube layout

Summary • non-planar domains – base complexes – spherical domains – polycubes • applications – remeshing – texture mapping – morphing Mesh Parameterization: Theory and Practice Non-Planar Domains