Mesh Generation Refinement and Partitioning Algorithms Xin Sui

Mesh Generation, Refinement and Partitioning Algorithms Xin Sui The University of Texas at Austin

Detailed classification

Delaunay Triangulation

Introduction • The Problem – Given a set of points – Output a triangulation of the set of points that satisfies the Delaunay Property (introduced soon) • Applications – Finite element analysis, computer graphics rendering, geometric modeling, etc Figure from Jernej Barbic’s slides Figure from Benoît Hudson’s slides(2007) Delaunay Triangulation

Delaunay Property • No vertex is inside the circumcircle of any triangle (vertices are permitted on the circle) • Maximize the minimum angle of all the angles of the triangles in the triangulation • Delaunay triangulation is unique if no four points share the same circumcircle Figure from Jonathan Shewchuk’s Ph. D thesis Delaunay Triangulation 5

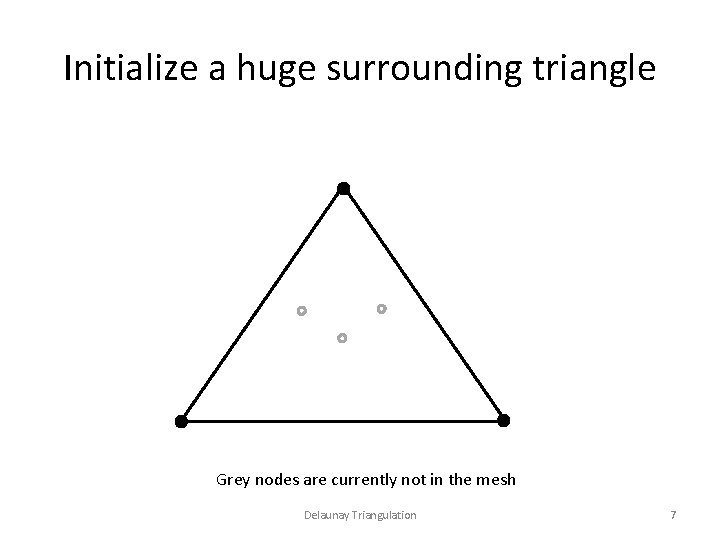
Triangulate the following points Grey nodes are currently not in the mesh Delaunay Triangulation 6

Initialize a huge surrounding triangle Grey nodes are currently not in the mesh Delaunay Triangulation 7

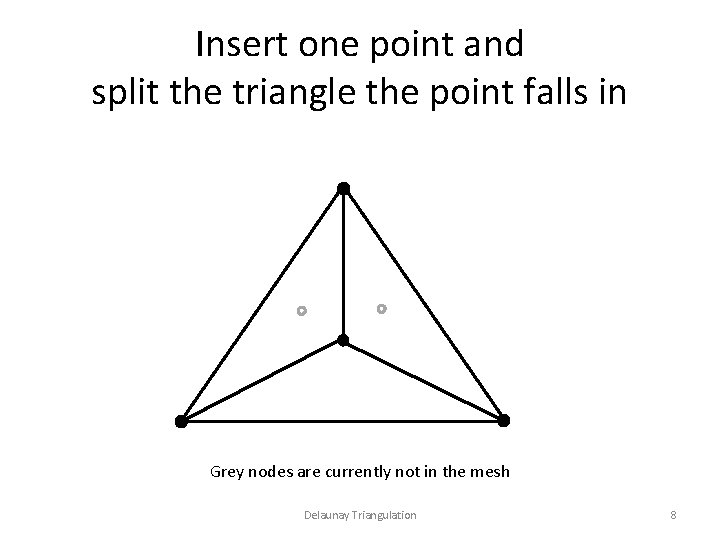
Insert one point and split the triangle the point falls in Grey nodes are currently not in the mesh Delaunay Triangulation 8

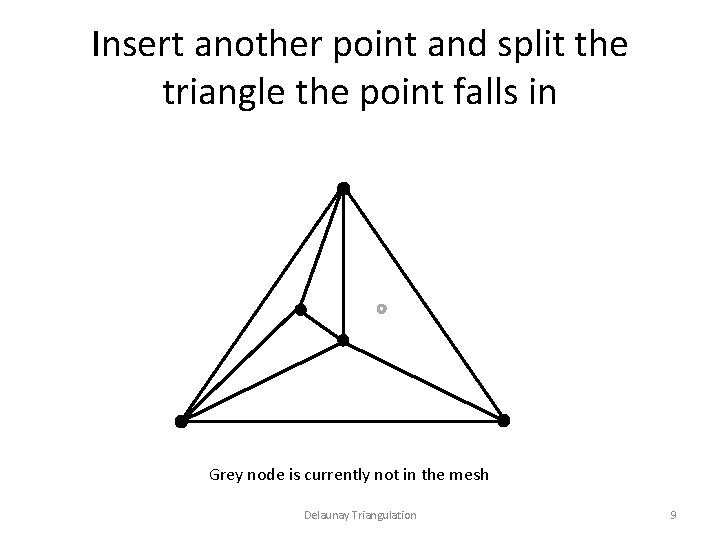
Insert another point and split the triangle the point falls in Grey node is currently not in the mesh Delaunay Triangulation 9

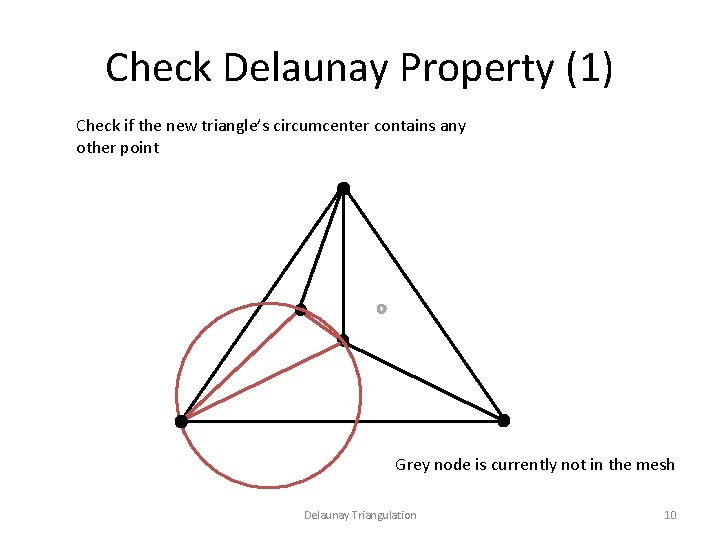
Check Delaunay Property (1) Check if the new triangle’s circumcenter contains any other point Grey node is currently not in the mesh Delaunay Triangulation 10

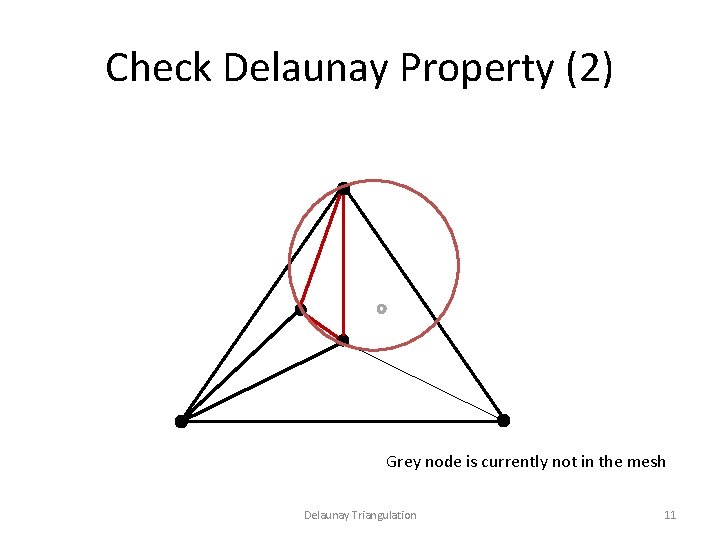
Check Delaunay Property (2) Grey node is currently not in the mesh Delaunay Triangulation 11

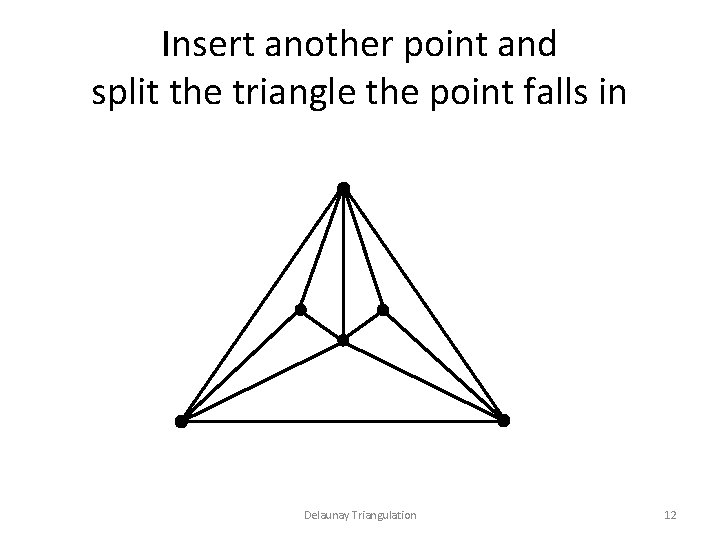
Insert another point and split the triangle the point falls in Delaunay Triangulation 12

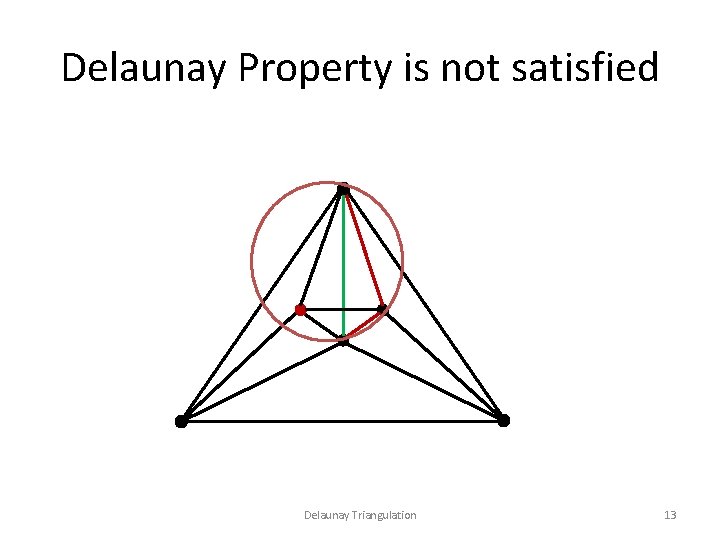
Delaunay Property is not satisfied Delaunay Triangulation 13

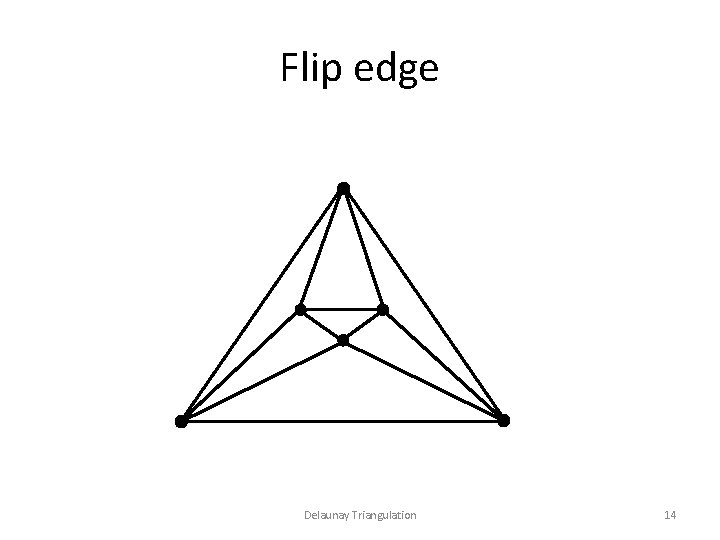
Flip edge Delaunay Triangulation 14

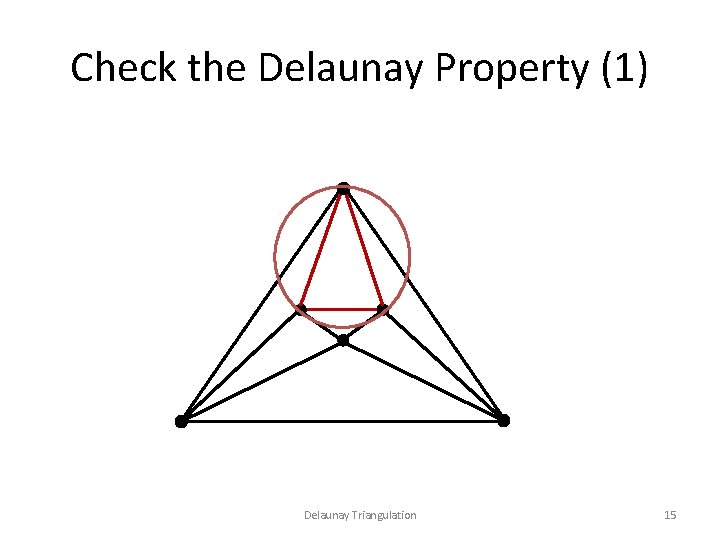
Check the Delaunay Property (1) Delaunay Triangulation 15

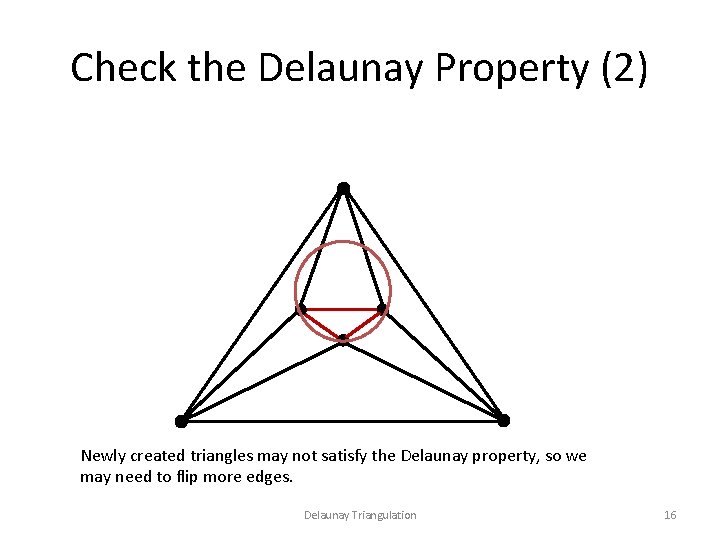
Check the Delaunay Property (2) Newly created triangles may not satisfy the Delaunay property, so we may need to flip more edges. Delaunay Triangulation 16

Pseudocode of DT 1: Mesh m = /* initialize with one surrounding triangle */ 2: Set points = /* read points to insert */ 3: Worklist wl; 4: wl. add(points); 5: foreach Point p in wl { 6: Triangle t = m. surrounding(p); 7: Triangle new. Split[3] = m. split. Triangle(t, p); 8: Worklist wl 2; 9: wl 2. add(edges(new. Split)); 10: for Edge e in wl 2 { 11: if (!is. Delaunay(e)) { 12: Triangle new. Flipped[2] = m. flip. Edge(e); 13: wl 2. add(edges(new. Flipped)) 14: }}} Delaunay Triangulation 17

Amorphous Data-Parallelism • Topology: graph • Operator: morph (refinement) • Active nodes: all the triangles containing points waiting for insertion • Ordering: unordered • Neighborhoods: The neighbor triangles of the split triangle and any triangles affected by edge flipping • Parallelism: increasing from none to a lot Delaunay Triangulation 18

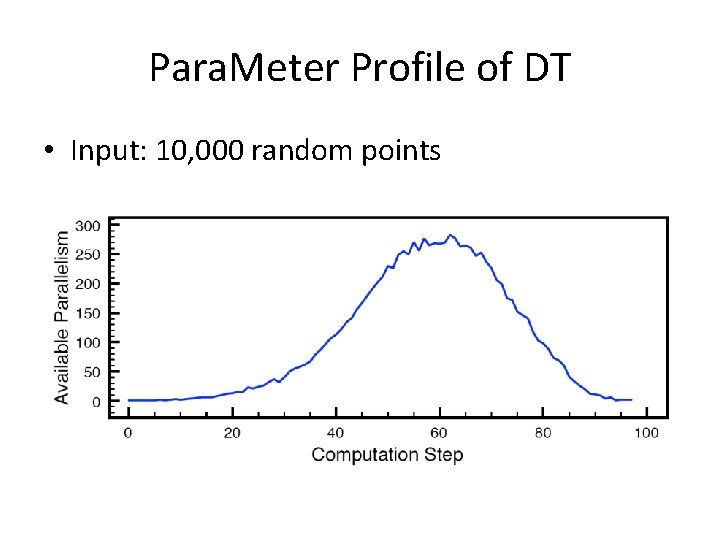
Para. Meter Profile of DT • Input: 10, 000 random points

Delaunay Mesh Refinement

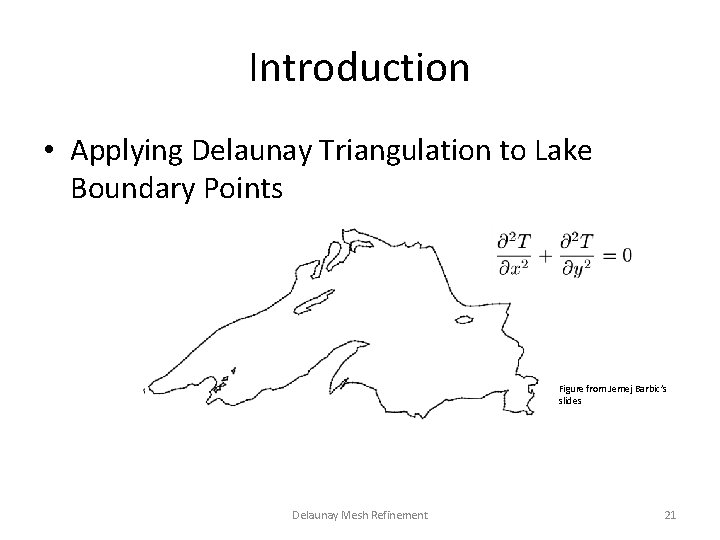
Introduction • Applying Delaunay Triangulation to Lake Boundary Points Figure from Jernej Barbic’s slides Delaunay Mesh Refinement 21

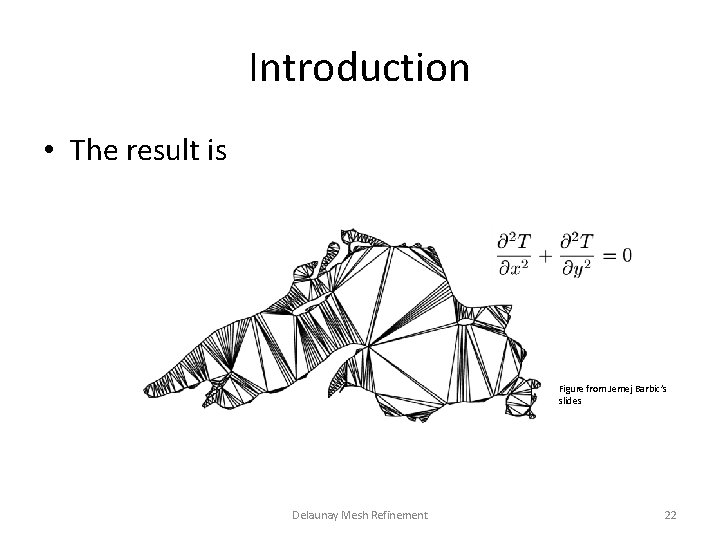
Introduction • The result is Figure from Jernej Barbic’s slides Delaunay Mesh Refinement 22

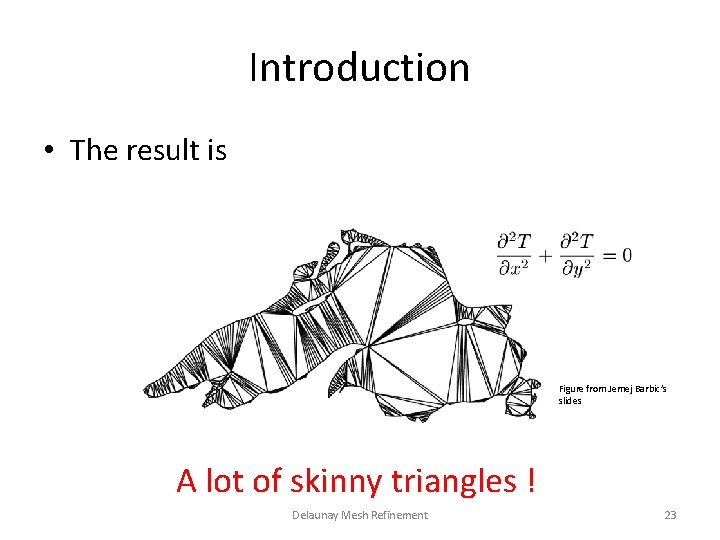
Introduction • The result is Figure from Jernej Barbic’s slides A lot of skinny triangles ! Delaunay Mesh Refinement 23

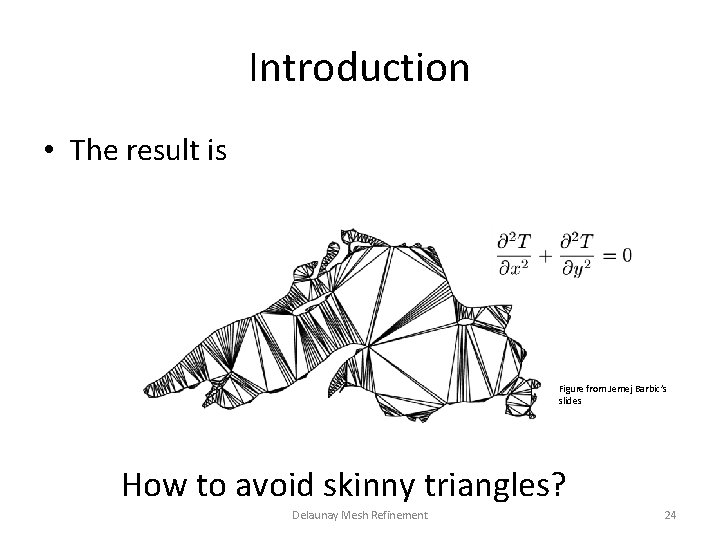
Introduction • The result is Figure from Jernej Barbic’s slides How to avoid skinny triangles? Delaunay Mesh Refinement 24

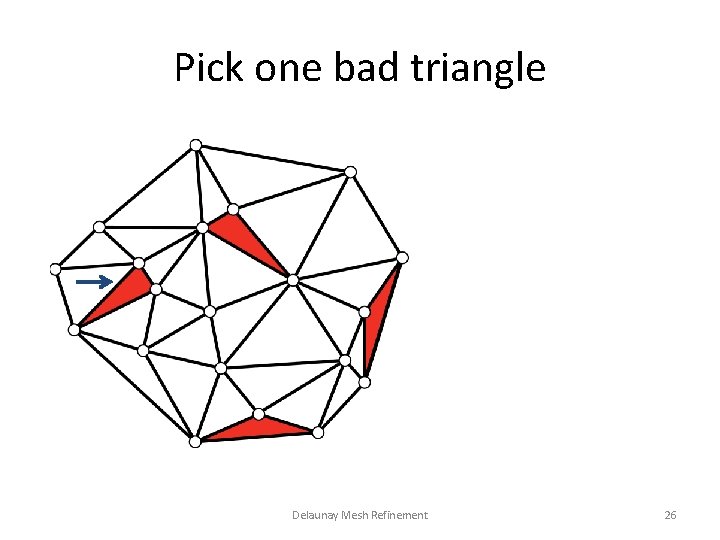
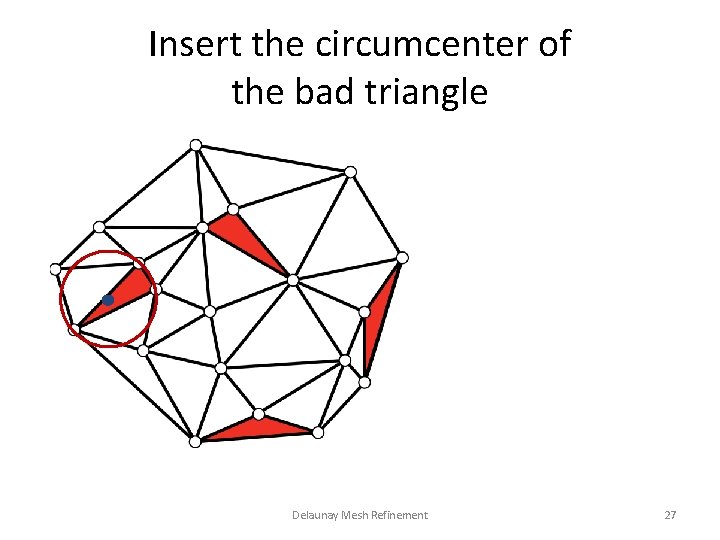
Delaunay Mesh Refinement • Eliminate bad triangles that do not satisfy quality criteria – Skinny triangles: triangle has a circumradius-toshortest edge ratio larger than some appropriate bound • The idea is adding the circumcenter of bad triangles into the mesh as additional mesh points Delaunay Mesh Refinement 25

Pick one bad triangle Delaunay Mesh Refinement 26

Insert the circumcenter of the bad triangle Delaunay Mesh Refinement 27

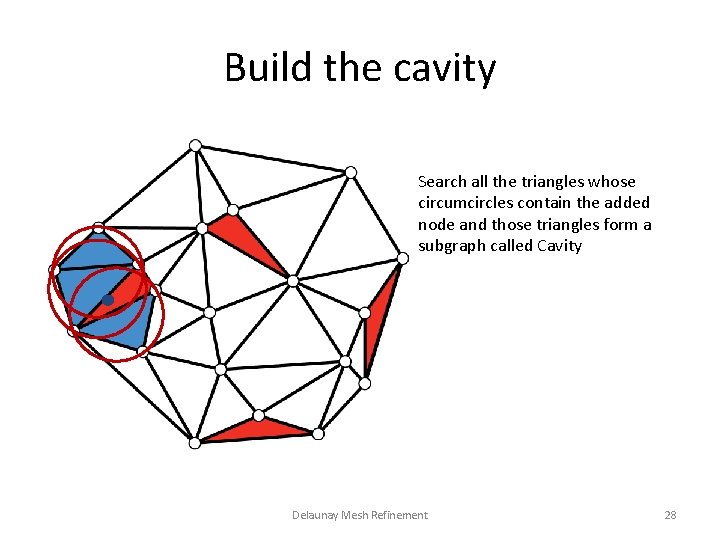
Build the cavity Search all the triangles whose circumcircles contain the added node and those triangles form a subgraph called Cavity Delaunay Mesh Refinement 28

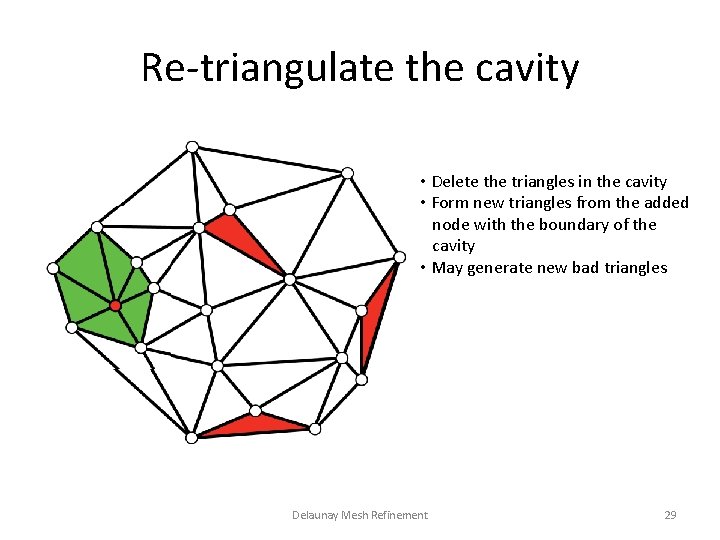
Re-triangulate the cavity • Delete the triangles in the cavity • Form new triangles from the added node with the boundary of the cavity • May generate new bad triangles Delaunay Mesh Refinement 29

Pseudocode of DMR 1: Mesh m = /* read input mesh */ 2: Worklist wl = new Worklist(m. get. Bad()); 3: foreach Triangle t in wl { 4: Cavity c = new Cavity(t); 5: c. build(); 6: c. retriangulate(); 7: m. update. Mesh(c); 8: wl. add(c. get. Bad()); 9: } Delaunay Mesh Refinement 30

Amorphous Data-Parallelism • • • Topology: graph Operator: morph (refinement) Active nodes: all the bad triangles Ordering: unordered Neighborhoods: cavities Parallelism: lots Delaunay Mesh Refinement 31

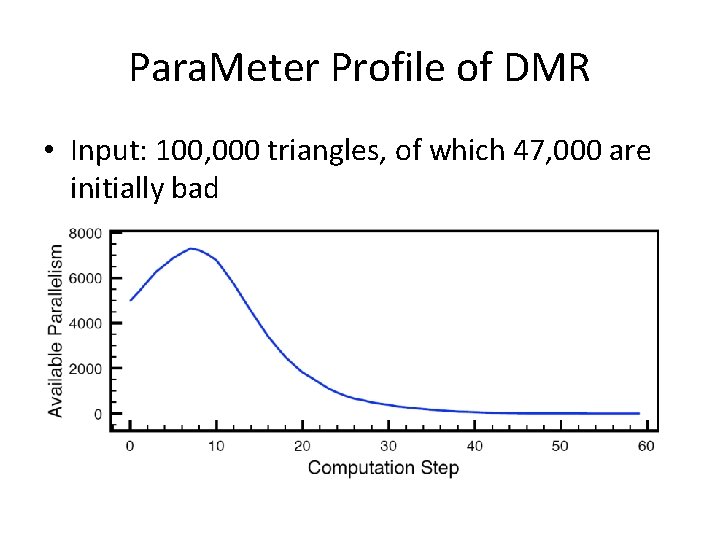
Para. Meter Profile of DMR • Input: 100, 000 triangles, of which 47, 000 are initially bad

Metis Graph Partitioning

Introduction • Metis (George Karypis, UMN) – Partitioning the nodes of a graph into k roughly equal parts, such that the number of edges connecting nodes in different parts is minimized – Multilevel scheme • Coarsening the graph into a very small graph • Partitioning the small graph • Projecting back the partitioning to original graph Metis Graph Partitioning 34

Introduction • Metis (George Karypis, UMN) – Partitioning the nodes of a graph into k roughly equal parts, such that the number of edges connecting nodes in different parts is minimized – Multilevel scheme • Coarsening the graph into a very small graph • Partitioning the small graph • Projecting back the partitioning to original graph Metis Graph Partitioning Our focus 35

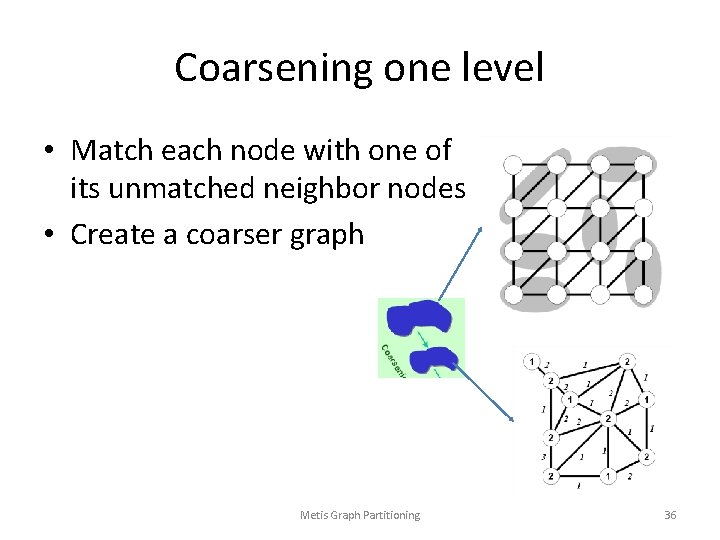
Coarsening one level • Match each node with one of its unmatched neighbor nodes • Create a coarser graph Metis Graph Partitioning 36

Pseudocode of Coarsening 1: Graph g=/*input graph*/ 2: Do { 3: Graph cg=new Graph(); 4: g. match. Nodes(); 5: cg. build. Graph(g); 6: g=cg; 7: } while (!g. coarse. Enough()) Metis Graph Partitioning 37

How to match nodes? • Maximal matching problem – NP-Complete – many heuristics • Random Matching Heuristic – The nodes in the graph are visited in random order – If a node u has not been matched yet, then randomly select one of its unmatched neighbor nodes – If there is no unmatched neighbor node, the node u matches to itself Metis Graph Partitioning 38

Visit a Node Metis Graph Partitioning 39

Match to a Neighbor Node Metis Graph Partitioning 40

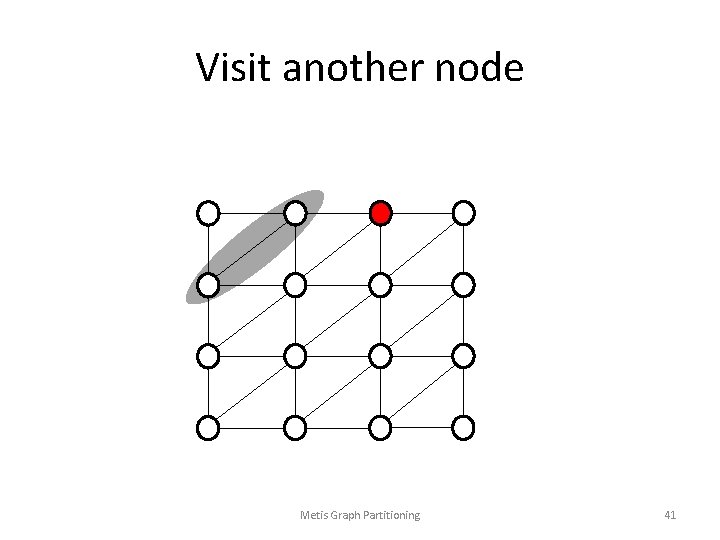
Visit another node Metis Graph Partitioning 41

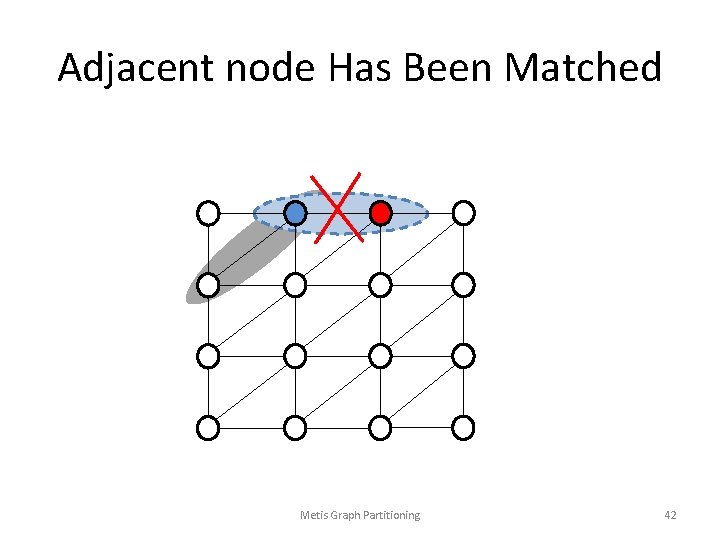
Adjacent node Has Been Matched Metis Graph Partitioning 42

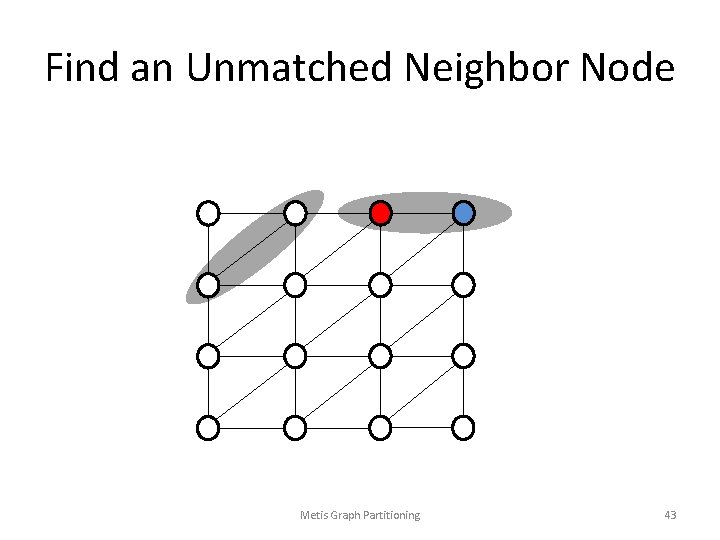
Find an Unmatched Neighbor Node Metis Graph Partitioning 43

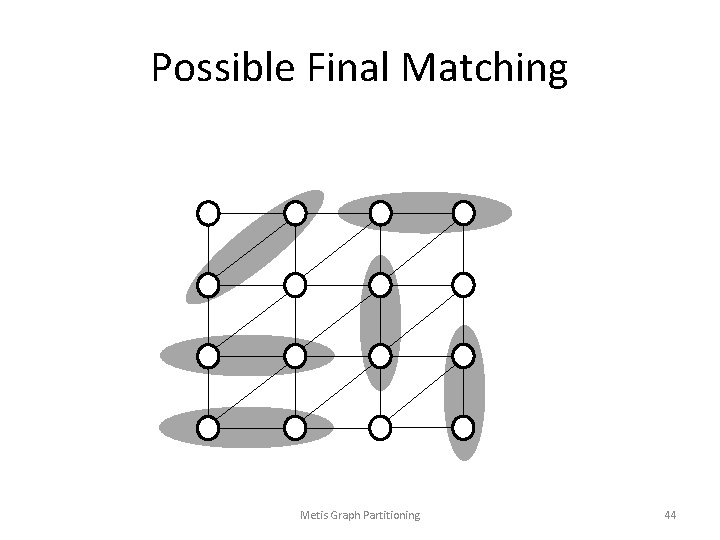
Possible Final Matching Metis Graph Partitioning 44

Pseudocode of Graph. match. Nodes() // Random Matching Heuristics 1: foreach Node n in graph{ 2: if n. is. Matched() continue; 3: Node match = n; 4: for Node neighbor in n. get. Neighbors(){ 5: if(!neighbor. is. Matched()){ 6: match =neighbor; 7: break; 8: } 9: } 10: set. Match(n, match); 11: } } Metis Graph Partitioning 45

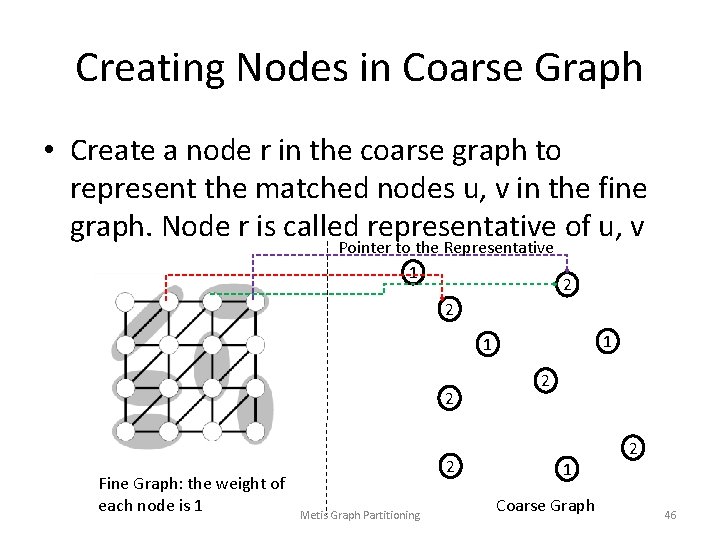
Creating Nodes in Coarse Graph • Create a node r in the coarse graph to represent the matched nodes u, v in the fine graph. Node r is called representative of u, v Pointer to the Representative 1 2 2 1 1 2 Fine Graph: the weight of each node is 1 2 Metis Graph Partitioning 2 1 Coarse Graph 2 46

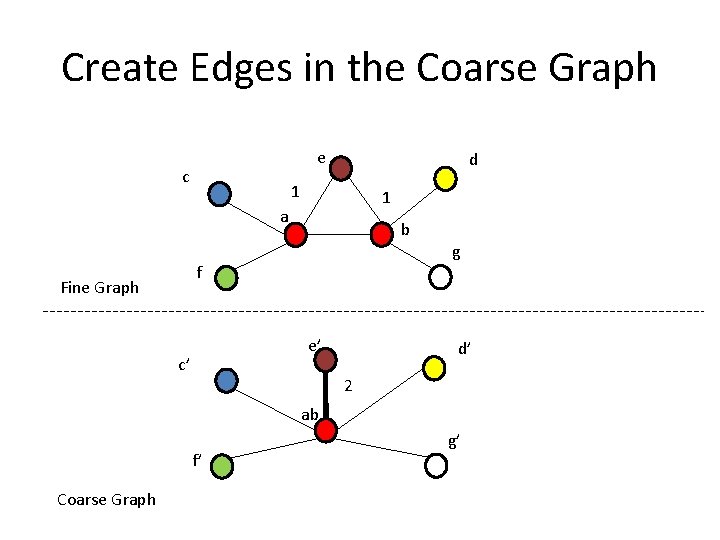
Create Edges in the Coarse Graph e c d 1 1 a b g f Fine Graph e’ c’ d’ 2 ab f’ Coarse Graph g’

Pseudocode of Graph. build. Graph(Graph fine. Graph) 1. Create Nodes in Coarse Graph 1: foreach Node n in fine. Graph { 2: if(n. isprocessed()) continue; 3: Node cn = create. Node(); //create Node for cg 4: n. set. Representative(cn); 5: Node match=n. get. Match(); 6: match. set. Representative(cn); 7: match. set. Processed(true); 8: } Metis Graph Partitioning 48

Pseudocode of Graph. build. Graph(Graph finer) 2. Create Edges for Coarse Graph 1: foreach Node n in finer { 2: if(n. is. Processed()) continue; 3: Node m=n. get. Match(); 4: Node r=n. get. Representative(); 5: create. Edges(r, n, m, finer); 6: if(n!=m){ 7: create. Edges(r, m, n, finer) 8: m. set. Processed(true); 9: } 10: } Metis Graph Partitioning //Build. Edges For Node r in the Coarse. Graph. create. Edges (Node r, Node n, Node match, Graph finer){ 11: for Node neigh in finer. get. Neighbors(n) { 12: if(neigh==match) continue; 13: Node nr=neigh. get. Representative(); 14: Edge e=finer. get. Edge(n, neigh); 15: Edge ce=get. Edge(r, nr); //create edge or adjust edge weight 16: if(ce==null) 17: create. Edge(r, nr, e. weight); 18: else 19: e. increase. Weight(e. weight); 20: } 21: } 49

Amorphous Data-Parallelism(1) • Match nodes in the fine graph – Topology: graph – Operator: local computation (structure-driven) – Active nodes: all the nodes in the graph – Ordering: unordered – Neighborhoods: active nodes’ neighbor nodes – Parallelism: lots Metis Graph Partitioning 50

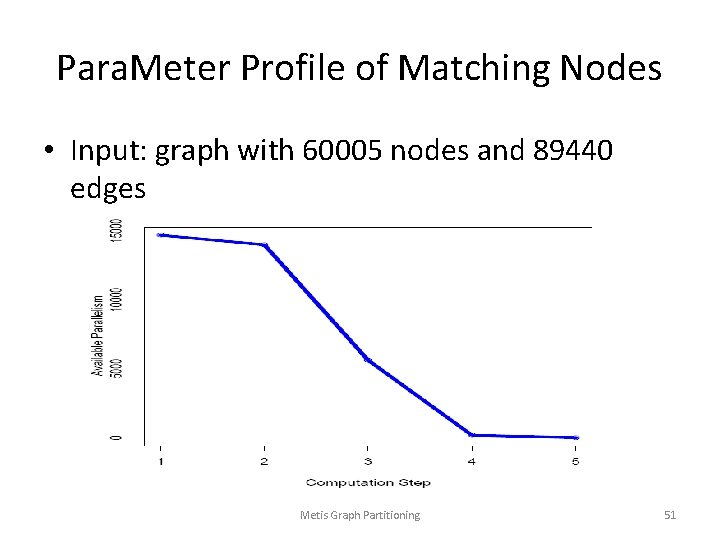
Para. Meter Profile of Matching Nodes • Input: graph with 60005 nodes and 89440 edges Metis Graph Partitioning 51

Amorphous Data-Parallelism(2) • Create nodes in the coarse graph – Topology: graph – Operator: morph (coarsening) – Active nodes: all the nodes in the fine graph – Ordering: unordered – Neighborhoods: active node’s matched node in fine graph and the representative nodes of the active node and its matched nodes in the coarse graph – Parallelism: lots Metis Graph Partitioning 52

Amorphous Data-Parallelism(3) • Create edges in the coarse graph – Topology: graph – Operator: morph (coarsening) – Active nodes: all the nodes in the fine graph – Ordering: unordered – Neighborhoods: active node u’s neighbor nodes in fine graph and u’s representative node’s neighbor nodes in the coarse graph – Parallelism: lots Metis Graph Partitioning 53

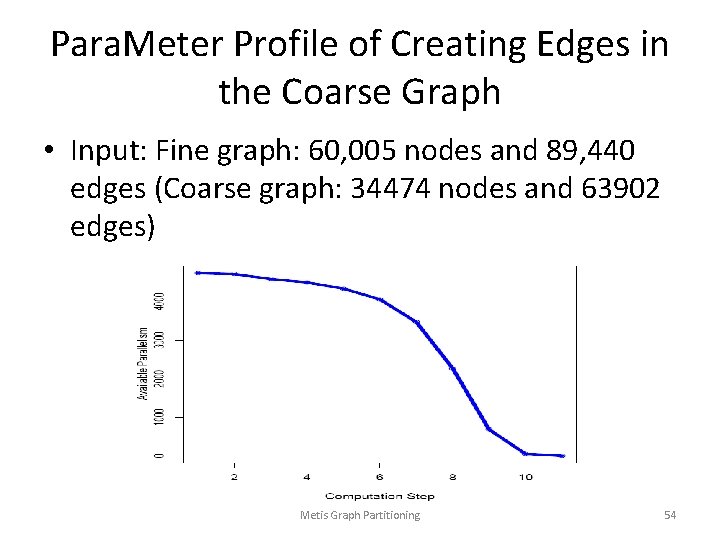
Para. Meter Profile of Creating Edges in the Coarse Graph • Input: Fine graph: 60, 005 nodes and 89, 440 edges (Coarse graph: 34474 nodes and 63902 edges) Metis Graph Partitioning 54

Thank you!