Mesh Analysis Mesh Analysis Loop Analysis Mesh A



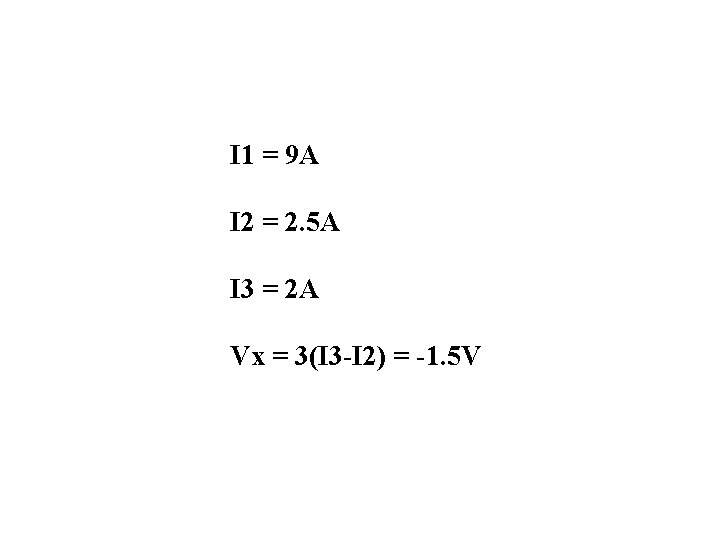





- Slides: 32

Mesh Analysis

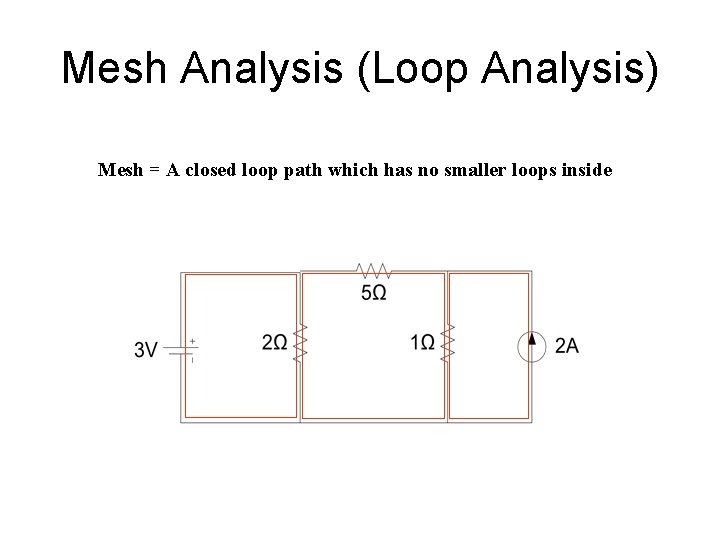
Mesh Analysis (Loop Analysis) Mesh = A closed loop path which has no smaller loops inside

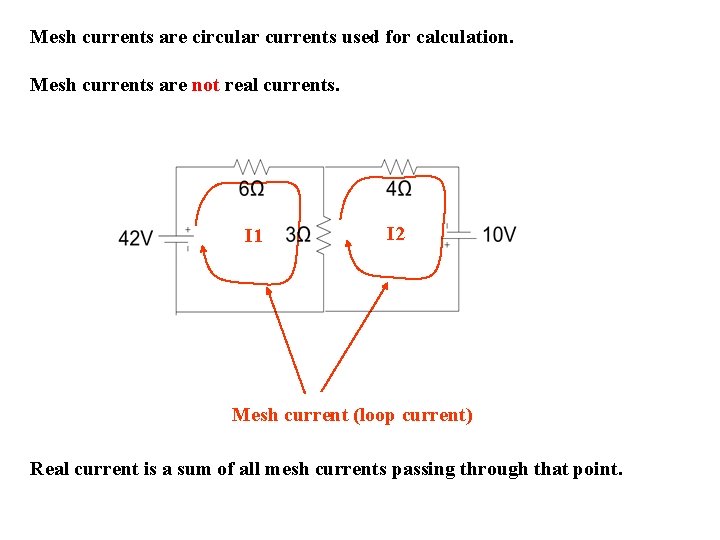
Mesh currents are circular currents used for calculation. Mesh currents are not real currents. I 1 I 2 Mesh current (loop current) Real current is a sum of all mesh currents passing through that point.

Mesh Analysis Procedure 1. Count the number of meshes. Let the number equal N. 2. Define mesh current on each mesh. Let the values be I 1, I 2, I 3, … 3. Use Kirchoff’s voltage law (KVL) on each mesh, generating N equations 4. Solve the equations

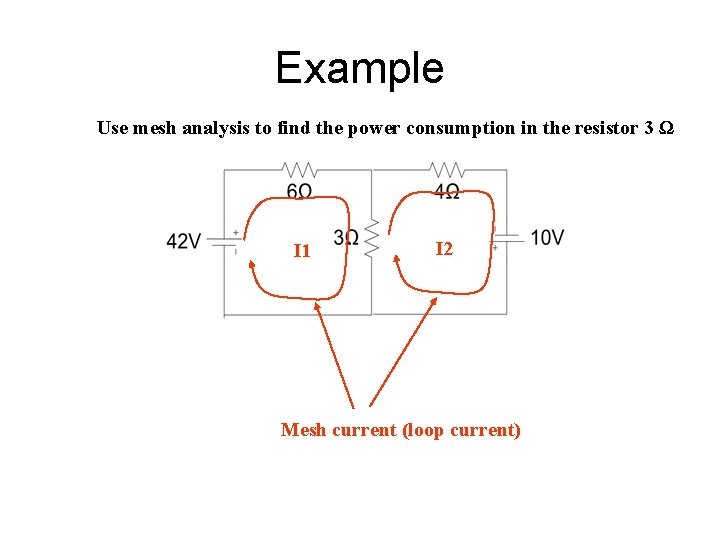
Example Use mesh analysis to find the power consumption in the resistor 3 Ω I 1 I 2 Mesh current (loop current)

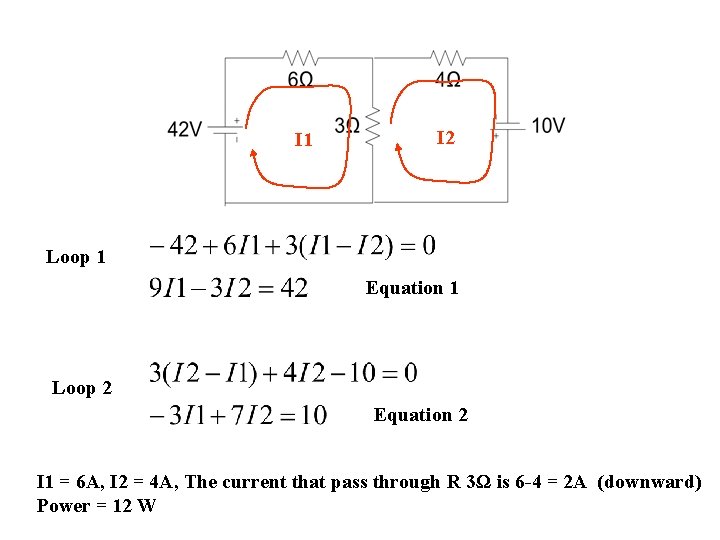
I 1 I 2 Loop 1 Equation 1 Loop 2 Equation 2 I 1 = 6 A, I 2 = 4 A, The current that pass through R 3Ω is 6 -4 = 2 A (downward) Power = 12 W

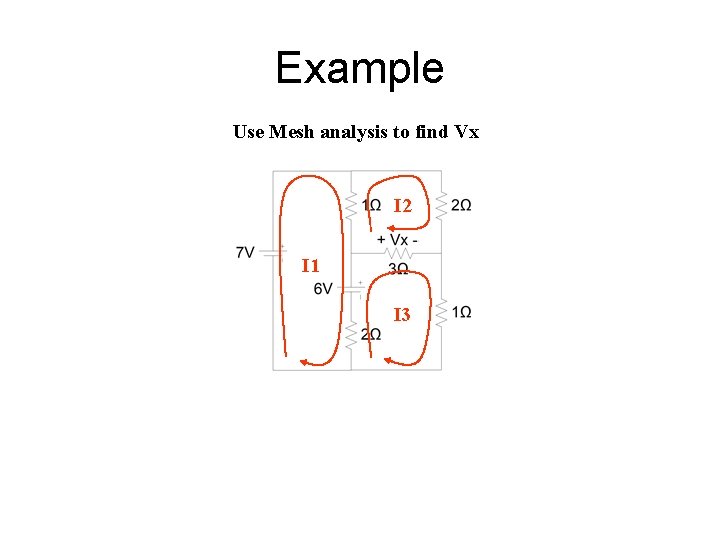
Example Use Mesh analysis to find Vx I 2 I 1 I 3

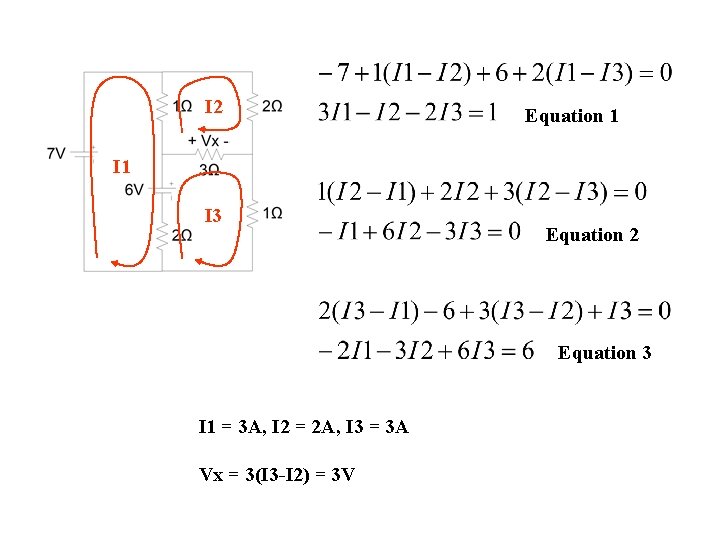
I 2 Equation 1 I 3 Equation 2 Equation 3 I 1 = 3 A, I 2 = 2 A, I 3 = 3 A Vx = 3(I 3 -I 2) = 3 V

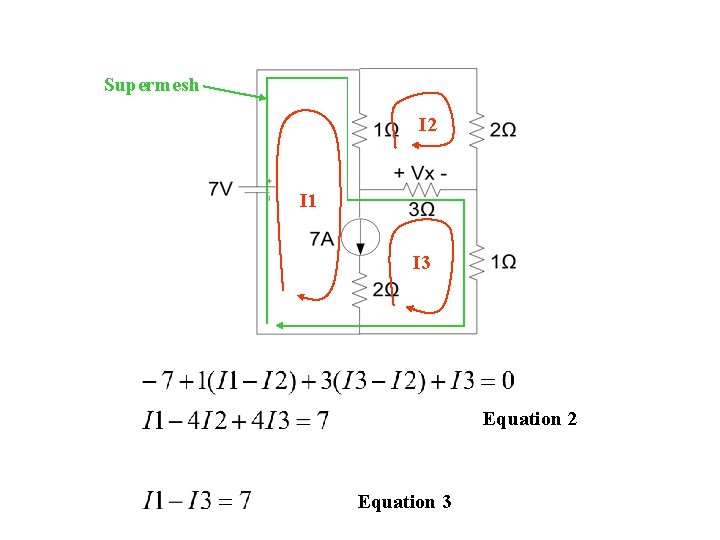
Supermesh When there is a current source in the mesh path, we cannot use KVL because we do not know the voltage across the current source. We have to use supermesh, which is a combination of 2 meshes to be a big mesh, and avoid the inclusion of the current source in the mesh path.

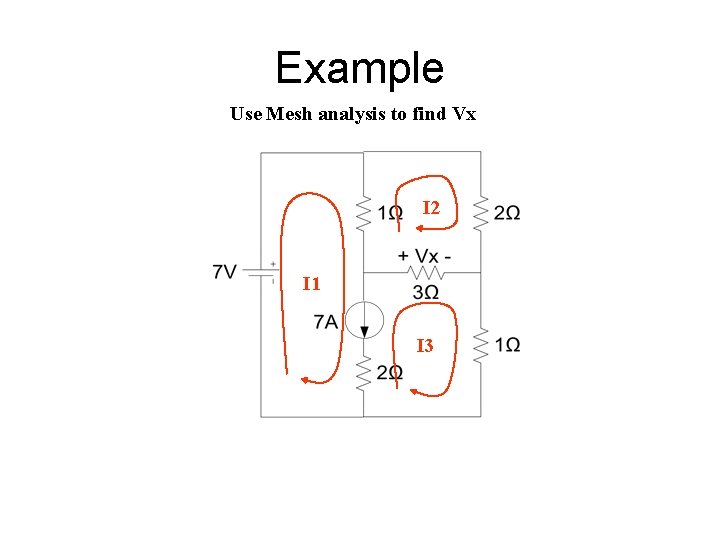
Example Use Mesh analysis to find Vx I 2 I 1 I 3

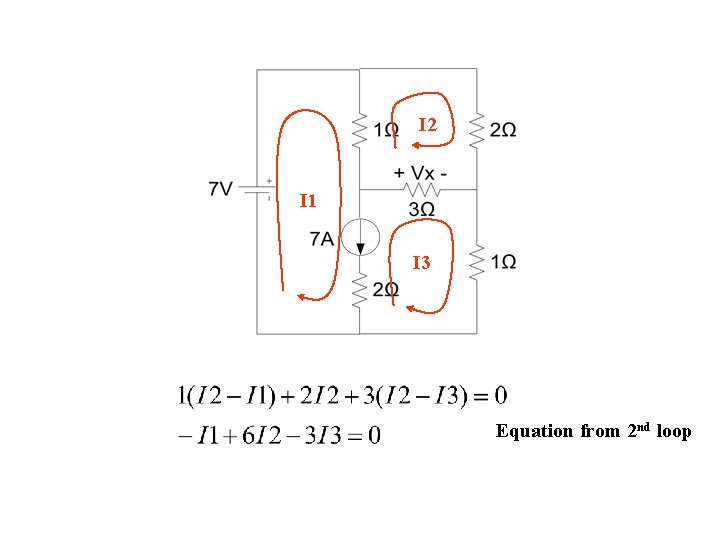
I 2 I 1 I 3 Equation from 2 nd loop

Supermesh I 2 I 1 I 3 Equation 2 Equation 3
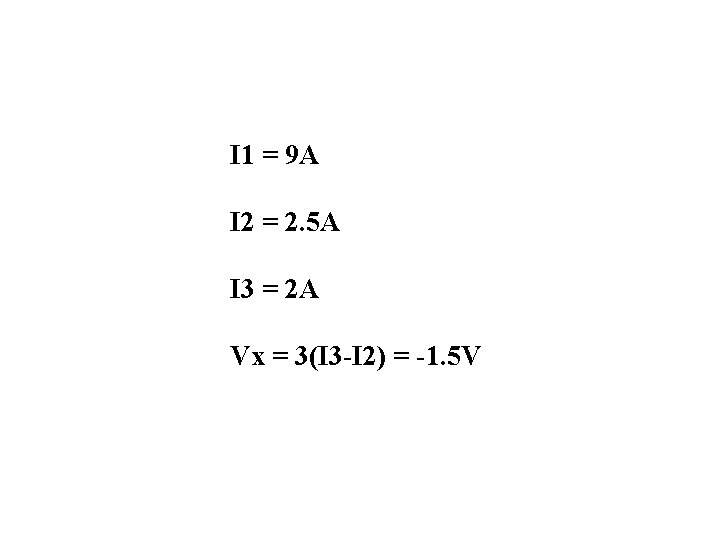
I 1 = 9 A I 2 = 2. 5 A I 3 = 2 A Vx = 3(I 3 -I 2) = -1. 5 V

How to choose between Node and Mesh Analysis The hardest part in analyzing circuits is solving equations. Solving 3 or more equations can be time consuming. Normally, we will count the number of equations according to each method and select the method that have lesser equations.

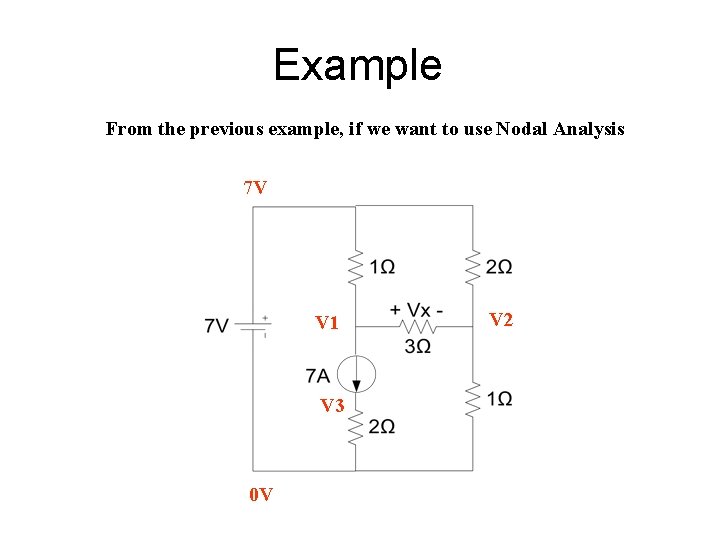
Example From the previous example, if we want to use Nodal Analysis 7 V V 1 V 3 0 V V 2

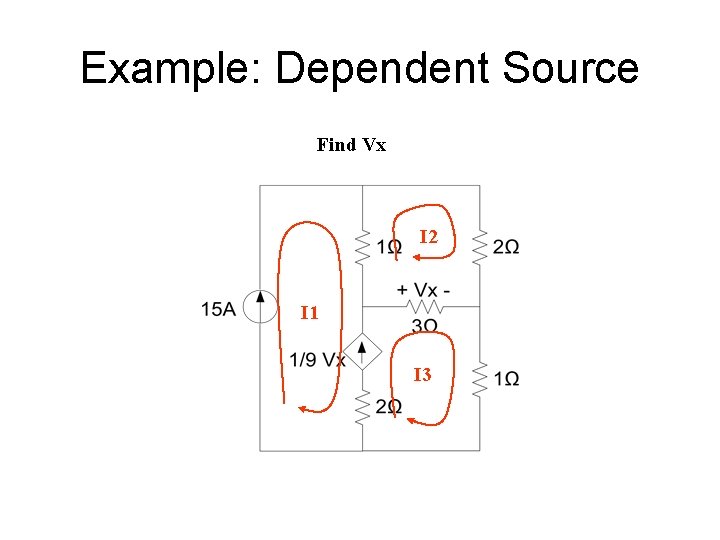
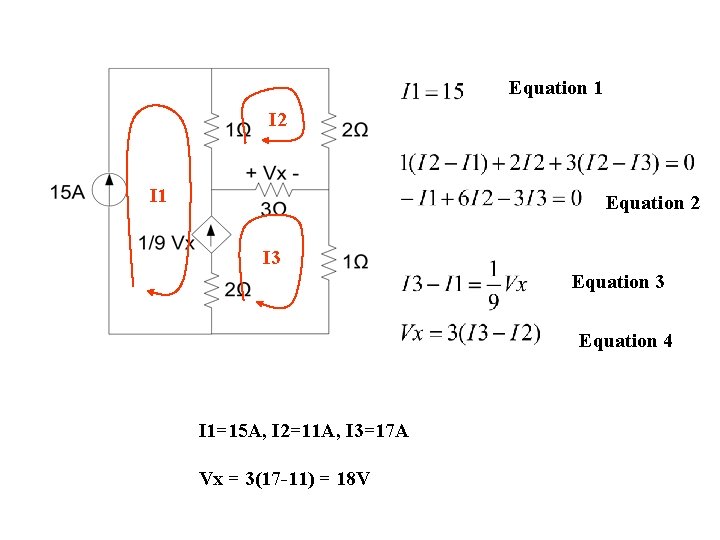
Example: Dependent Source Find Vx I 2 I 1 I 3

Equation 1 I 2 I 1 Equation 2 I 3 Equation 4 I 1=15 A, I 2=11 A, I 3=17 A Vx = 3(17 -11) = 18 V

Special Techniques • Superposition Theorem • Thevenin’s Theorem • Norton’s Theorem • Source Transformation

Superposition Theorem In a linear circuit, we can calculate the value of current (or voltage) that is the result from each voltage source and current source independently. Then, the real value is the sum of all current (or voltage) from the sources.

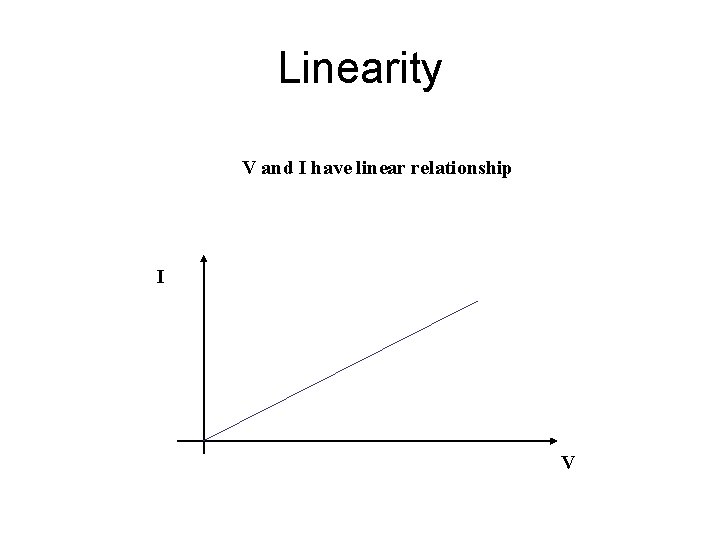
Linearity V and I have linear relationship I V

Implementation When calculating the effect of a source, the other sources will be set to zero. • For voltage sources, when set as 0 V, it will be similar to short circuit • For current sources, when set as 0 A, it will be similar to open circuit

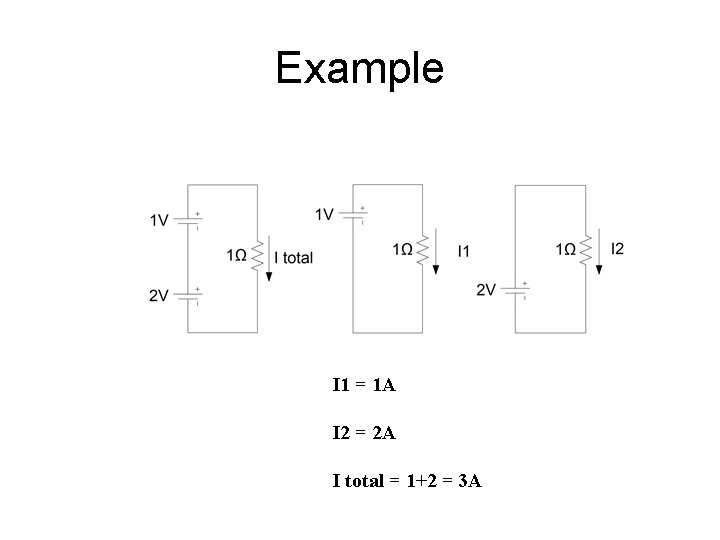
Example I 1 = 1 A I 2 = 2 A I total = 1+2 = 3 A

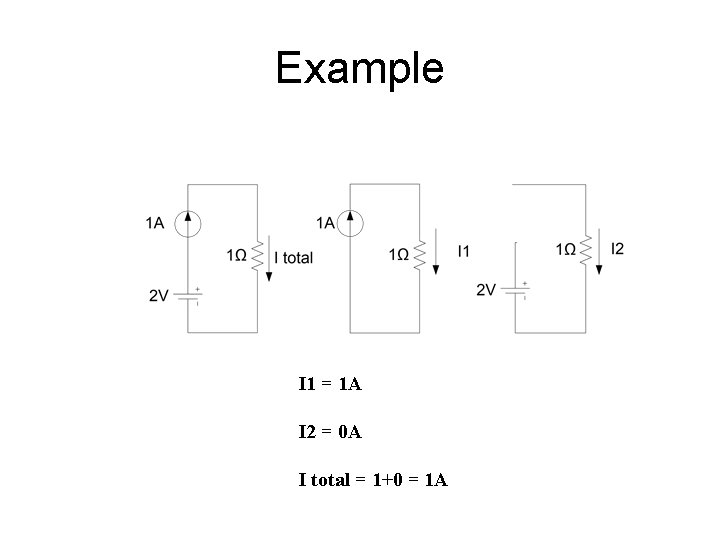
Example I 1 = 1 A I 2 = 0 A I total = 1+0 = 1 A

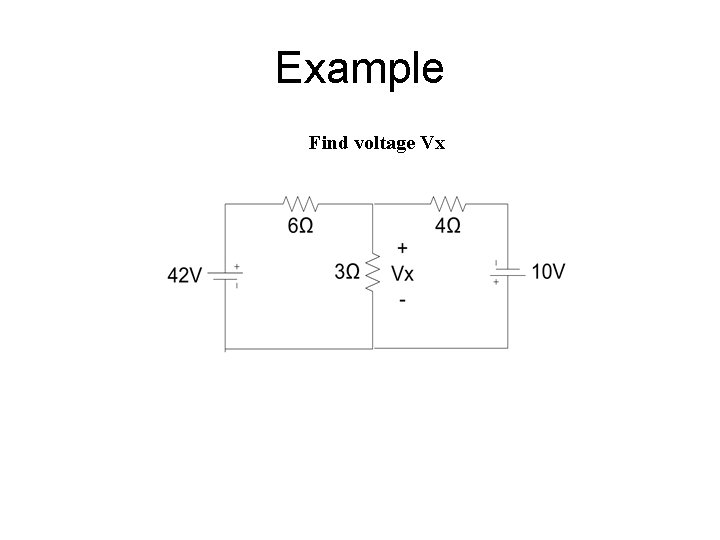
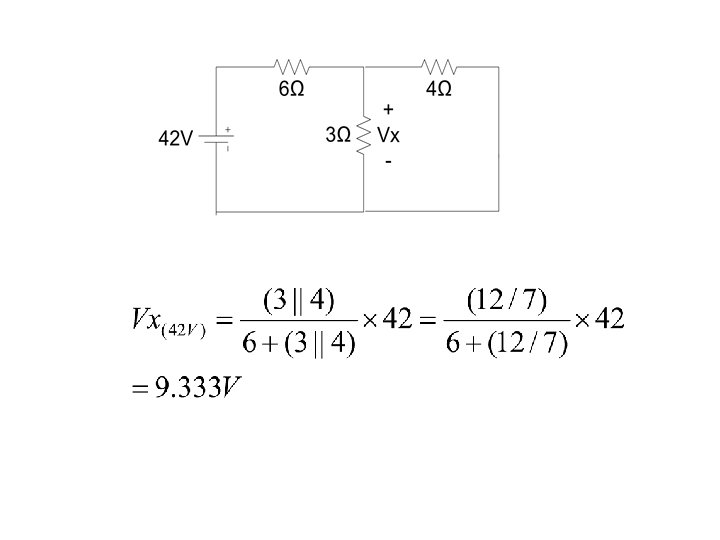
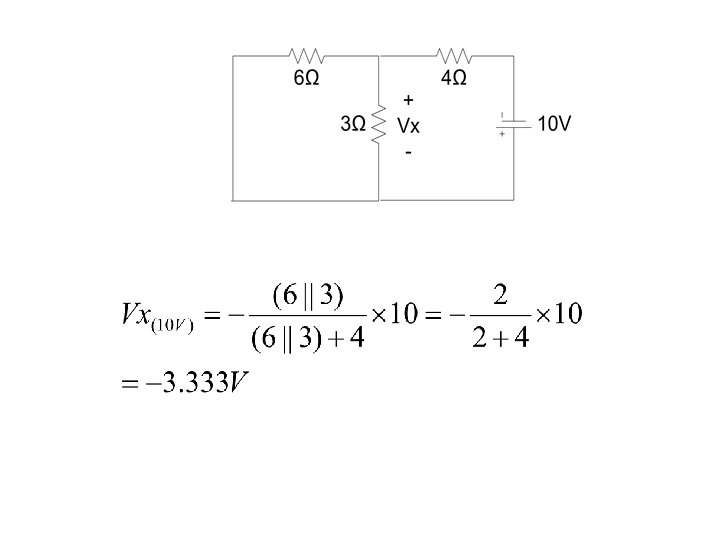
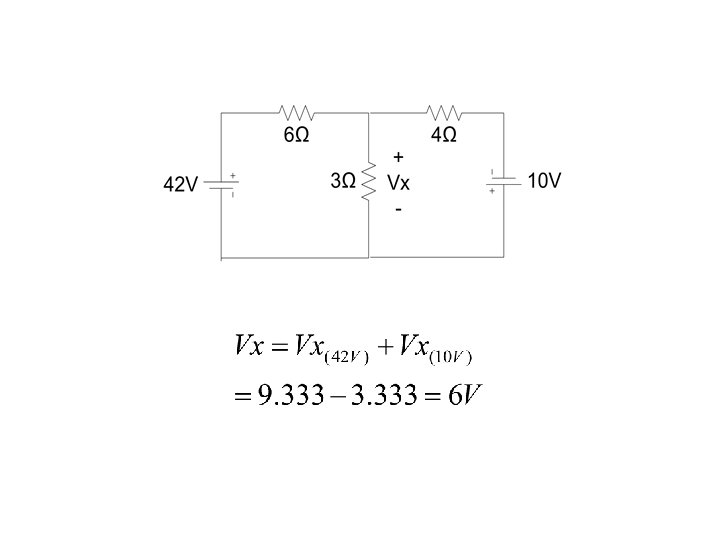
Example Find voltage Vx




Superposition and Dependent Source Dependent sources cannot be used with superposition. They have to be active all the time.

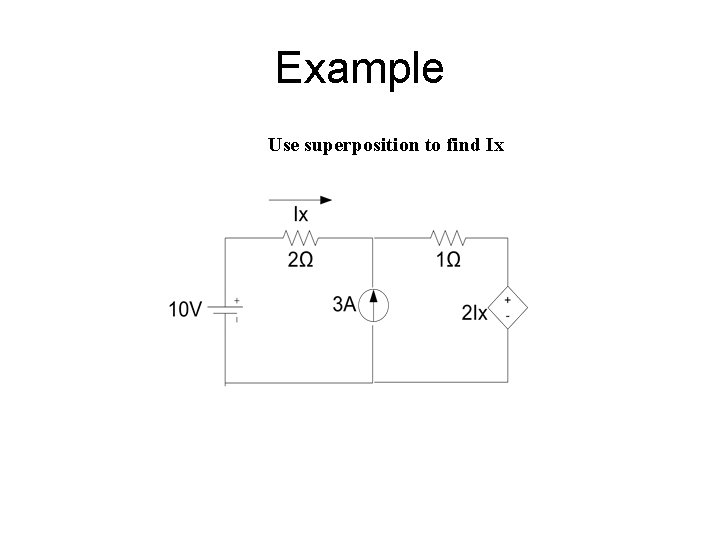
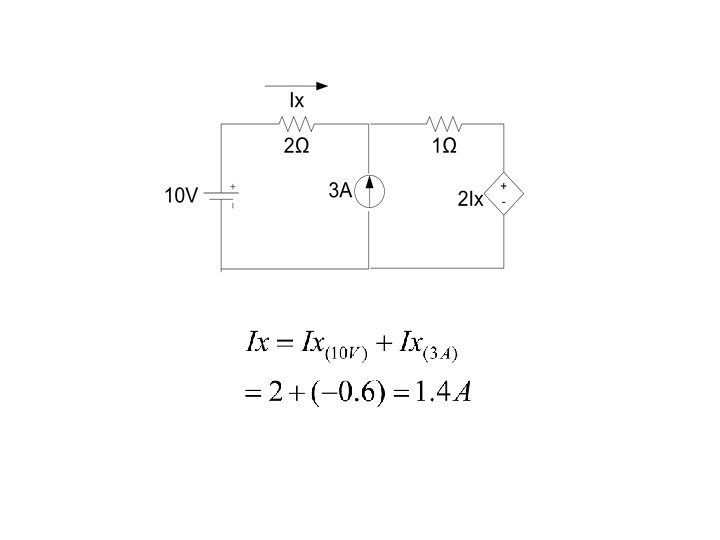
Example Use superposition to find Ix

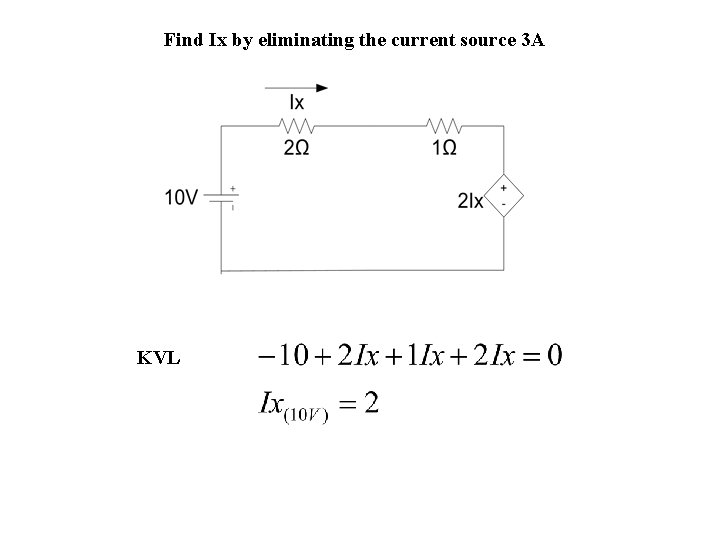
Find Ix by eliminating the current source 3 A KVL

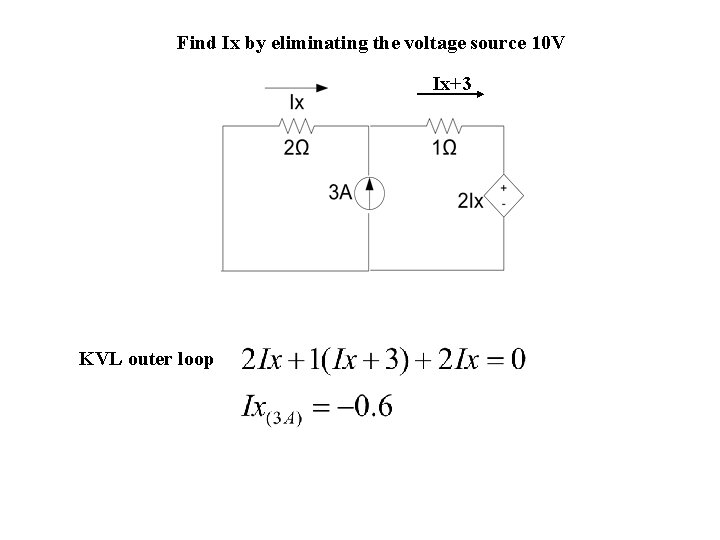
Find Ix by eliminating the voltage source 10 V Ix+3 KVL outer loop
