Merkezi Eilim ve Merkezi Dalm lleri Hsna BASTEM097126005

Merkezi Eğilim ve Merkezi Dağılım Ölçüleri Hüsna BASTEM-097126005 Elif ÖZDENTÜRK-047125003 EMİNE EVRİM ARLI-097126006

TANIMLAYICI İSTATİSTİK • Tanımlayıcı istatistikler verilerin sayısal ya da grafiksel olarak özetlenmesidir. Çalışmada veriler toplandıktan sonra, bunların merkezi eğilimleri, yayılımları, çarpıklıkları araştırılır.

• Ölçme sonuçlarına bakarak, grup hakkında ya da eğitim sistemi hakkında bazı kararlar verebilmek ve anlam çıkarabilmek için ölçme sonuçları üzerinde istatistik işlemlerinin yapılması gerekmektedir.

• Verilerin düzenlenmesi, veri grubunun tamamı hakkında bir ölçü. vermediğinden, düzenlenmiş verilerin yorumlanması ve daha anlamlı hale getirilmesi için merkezi eğilim ve merkezi dağılım ölçülerinden yararlanılmaktadır.

MERKEZİ EĞİLİM ÖLÇÜLERİ • Merkezi eğilim ölçüleri , puan dağılımında verilerin hangi puan etrafında toplandığı hakkında bilgi veren ve veri grubunu özetleyen değerlerdir. • Merkezi eğilim ölçüsü olarak mod, aritmetik ortalama, medyan gibi istatistiksel tanımlar kullanılmaktadır.

Aritmetik Ortalama • Aritmetik ortalama, değerler toplamının değer sayısına bölümü şeklinde tanımlanır. Bu tanıma göre aritmetik ortalama şöyle formüle edilir. • Frekanslar söz konusu olduğunda, sınıflandırılmış seriler için,

• Örnek olarak, bir sınava giren toplam öğrenci sayısı 7 olsun. Bu 7 öğrencinin sınavdan aldıkları notlar ise 100 üzerinden 60, 35, 28, 77, 81, 72 ve 74 olsun. O halde yukarıdaki formülü kullanarak bu sınav sonucundaki aritmetik ortalamayı hesaplayabiliriz: • Aritmetik ortalama = (60+35+28+77+81+72+74) / 7 = 61’dir.

Frekans serisi aritmetik ortalama örneği Xi fi fi. Xi 10 2 20 11 3 33 12 5 60 13 8 104 14 14 196 15 18 270 16 15 240 17 12 204 18 10 180 19 6 114 20 4 80 21 3 63 100 1564

• Toplam puanların puan sayısına (öğrenci sayısına )bölünmesi ile aritmetik ortalama bulunur. Aritmetik ortalamanın hesaplanmasında, puan dağılımındaki her puan hesaplamaya dahil edildiğinden, diğer merkezi eğilim ölçülerine göre aritmetik ortalama daha çok tercih edilen bir istatistiktir.

• Dağılışların yerinin belirlenmesinde en çok kullanılan yer ölçüsü aritmetik ortalamadır; ve tek başına ortalama sözcüğünden aritmetik ortalama anlaşılır. • Aritmetik ortalama bütün değerlerin ağırlığını eşit kabul ettiğinden dağılımı her zaman en iyi şekilde temsil etmeyebilir. Ayrıca aritmetik ortalama, veri kümesindeki aşırı değerlerden çok kolay etkilenir.

• Not: Aritmetik ortalama hesaplanırken her bir puanın ortalamaya katkı oranı aynıdır. • Puanlar farklı olduğunda katılım miktarları farklıdır, fakat katılım oranları(yüzde olarak) aynıdır.

Ağırlıklı Ortalama • Puanların ortalamaya katkı oranlarının farklı olması gerektiği durumlarda aritmetik ortalama yerine ağırlıklı ortalama hesaplanabilir. • Sınavların farklı kapsama sahip olmaları ya da farklı önem dereceleri ağırlıklı ortalama kullanmalarını gerektirir.

• Ağırlıklı ortalama; veri kümesindeki bütün değerlerin aynı ağırlığa (öneme) sahip olmadıkları durumlarda kullanılır. • 1’den n’e kadar olan bir veri kümesinde X’ler veri değerleri ve W’lar her bir X için bir ağırlık fonksiyonu olarak kabul edilirse; ağırlıklı ortalama formülü şöyle oluşur: 13

• Ağırlıklı ortalama eğitimde yaygın olarak kredili ders sistemindeki ortalamaların hesaplanmasında kullanılmaktadır. Örnek: İktisat, İşletme, Hukuk ve İngilizce derslerini alan bir öğrencinin ders kredisi / ders notu çizelgesi şöyledir: Ders Kredisi Ders Notu İktisat 4 75 İşletme 3 70 Hukuk 2 60 İngilizce 2 90 • O halde ağırlıklı ortalaması; (4 x 75)+(3 x 70)+(2 x 60)+(2 x 90)=73. 63 11 14

Örnek Ders Kredi Not Ağ. Not Fiz 101 4 AA (4. 0) 16. 0 Kim 101 4 BB (3. 0) 12. 0 Müh 100 2 BA (3. 5) 7. 0 Mat 101 CB (2. 5) 10. 0 4 Türk 101 2 CC (2. 0) 4. 0 İng 101 2 DD (1. 0) 2. 0 MAK 101 3 DC (1. 5) 4. 5 Toplam 21 55. 5 • Yandaki tabloda verilen ders ve notlar için ağırlıklı ortalama:

Medyan(Ortanca) • Büyüklük sırasına göre düzenlenmiş puanlar dizisinin tam ortasına düşen puandır. • Ortanca hesaplanırken mutlaka verilerin sıraya konulmuş olması gerekmektedir. • Ölçülen değerler küçükten büyüğe ya da büyükten küçüğe doğru dizildiği zaman grubun, dizinin tam ortasındaki , yani yüzde ellinci puan veya ölçümüdür.

• Denek sayısı çiftse, ortadaki iki deneğin ortalamaları alınır. • Aşırı değerlerden etkilenmez. • Verilerde sapan değerler var ise ortanca verileri ortalamadan daha iyi betimler. – Örnek: Şu an bu sınıftaki kişilerin yaş ortalaması.

Seri birimlerinin tek sayıda olması durumunda serinin ‘inci biriminin değeri medyan olacaktır. (tek sayıda gözlem var ise ortanca orta değerdir) Seri birimlerinin çift sayıda olması durumunda ise, serinin ‘inci ve ‘inci birimlerinin değerlerinin ortalaması olarak kabul edilmektedir. ( çift sayıda gözlem var ise ortanca iki orta değerin ortalamasıdır)

Örnek: Aşağıda verilen serilerin medyanlarını hesaplayınız Xi : 2; 4; 7; 11; 13; 17 Yi: 3; 9; 13; 17; 19; 23; 2 Xi serisi, 7 birimli bir seri medyanı 4. birimin değeri olan 11 dir. Yi serisi 8 birimli bir seri olduğundan serinin medyanı 4’üncü ve 5’inci birimlerin değerlerinin ortalamasına eşittir.

Medyanın avantajları: • Hesaplanması ve anlaşılması kolaydır. • Uç değerlerden etkilenmez • Her dağılımda bir tane ortanca vardır.

Medyanın Dezavantajları: • Standart sapması ortalamanın standart sapmasından büyüktür. • Büyük veri yığınlarında bilgisayar kullanmadan hesaplanması zordur. • Ortanca, ölçüm sayısına eklenecek herhangi bir değerden hemen etkilenir ve değişir.

Mod(Tepe değeri) • Bir veri grubunda en çok tekrarlanan, yani frekansı en yüksek olan puandır. • Tepe değer verilerin en çok hangi değer etrafında toplandığı hakkında bilgi verir. • Mod en kararsız ölçüdür. • Eğer puan dizisinde her puan aynı frekansa sahipse o puan dizisinin modu yoktur. • Bir seride birden fazla mod olabilir. Bu durumda değişken çok modlu olarak nitelendirilir.

• Mod pratik olarak , bir seride en çok rastlanan, en çok tekrarlanan terim olarak tanımlanabilir. Eğer serinin histogramı çizilirse, en yüksek sütunun değeri serinin modudur. Bu sebepten mod’a tepe değeri de denir. • Tıpta nadir kullanılan bir merkezi eğilim ölçütüdür.

TEPE DEĞERİNİN ÖZELLİKLERİ • Hesaplanması ve anlaşılması kolaydır • Dağılımdaki aşırı değerlerden etkilenmez • Grafik üzerinde hiç işlem yapmadan, gözlenebilen tek ölçüdür. • Bazı dağılışlarda tepe değeri bulunmayabilir, bazılarında da birden fazla tepe değeri bulunabilir. İki tepe değeri bulunan dağılışlara bimodal dağılış adı verilir.

• Bazı dizilerde “tek mod” vardır. • 20, 30, 40, 50, 50, 60 • Dizidenin modu: 50 • Bazı dizilerde mod olabilecek değerler arda geldiğinde bunların ortalaması alınarak moda ulaşılır. • 20, 30, 40, 50, 60 • Dizinin modu: 45

• Bazı dizilerde birden fazla mod vardır. • 20, 30, 40, 40, 50, 60, 60, 7 0 • Dizinin modları: 40 ve 60 • 20, 30, 40, 50, 60 • Dizinin modları: 30 ve 55 • 20, 30, 40, 50, 60, 70, 8 0 • Dizinin modları: 35 ve 70

• Bazı dizilerde mod yoktur. • 20, 20, 30, 30 • 20, 30, 40, 50, 60, 70 • 20, 20, 30, 30, 30 • 0, 0, 0, 100, 100 • Puanlar frekans sayıları açısından farklılaşma göstermediklerinden dizide mod bulunamaz.

• Aynı zamanda puanlar farklılaşma göstermediğinde de mod aranmaz. • 20, 20, 20, 20

Merkezi Dağılım (Değişim )Ölçüleri • Merkeze yığılma ölçüleri, üzerinde ölçme yapılan grubu tanımamıza yardım eder. Ne var ki merkezi yığılma ölçüleri bir grubu tam olarak tanıtmaz. Bu ölçülere ek olarak puanların değişiklik (dağılım)ölçülerinin de bilinmesine gerek vardır.

• Farklı grupların merkezi eğilim ölçütleri aynı olduğu halde, gruplar birbirlerinden çok farklı olabilir. Bu nedenle merkezi eğilim ölçütleri yanında, yayılma ölçütleri de çok önemlidir.

• Merkezi dağılım ölçüleri, verilerin yığılma gösterilen noktadan ne kadar uzakta olduklarını, nasıl bir dağılım gösterdiklerini belirleyen istatistiklerdir. • Başlıca dağılım ölçüleri puan genişliği(ranj), standart sapma ve varyansdır.

Yayılım Ölçüleri • Puanlar arsındaki farklılaşma miktarını gösterir. (homojenheterojen) • Standart sapma en hassas yayılım ölçüsüdür. • Herhangi birinin 0 olması durumunda diğer yayılım ölçüleri de 0 olur. • Bütün notlar aynı olduğunda, bütün yayılım ölçüleri 0 olur.

Dağılım Aralığı (Range, DA) • Bir dizideki en büyük değer (Xmax) ile en küçük değer (Xmin) arasındaki farktır. • DA= (Xmax) - (Xmin) biçiminde hesaplanır. • 71 -68 -75 -44 -75 -81 -75 -94 -56 -75 -69 veri setinin dağılım aralığı nedir? • DA=94 -44=50’dir. 33

– Örnek: A üniversitesinin B bölümünün tavan puanı 361 ve taban puanı 349 ise. • En düşük (Minimum) = 349 puan • En yüksek (Maksimum) = 361 puan • Değişim aralığı = 361 -349 = 12 puan

• Ranj bir veri grubunun hangi aralıkta değişkenlik gösterdiğini belirten istatistiktir. • Ranj, puan dağılımları hakkında yüzeysel bilgi verir. • En basit yaygınlık ölçüsüdür.

• Ortalama gibi, uç değerlerden çok etkilenir. • En uçtaki iki değer arasında kalan değerler hakkında bilgi vermez. • Ekstrem değerlere duyarlı olan DA yer ölçülerinde olduğu gibi, bize dağılımın şekliyle ilgili bir şey söylememektedir.

• Ranj yeterince güvenilir değil, en basit yayılım ölçüsüdür. • 20, 60, 80, 70, 90, 80 Ranj: 90 -20=70 • 20, 20, 90, 20, 20 Ranj: 9020=70 • 2 grup hiç benzemiyor ama ranjları aynıdır.

Standart Sapma Bir veri grubunda verilerin aritmetik ortalamadan ne kadar uzaklaştığının ölçüsüdür. Puanların ortalamadan olan farklarının, kareleri toplamının ortalamasının, kareköküne eşittir. Örnek: 78, 89, 56, 36, 48, 92, 59, 60 S=19. 8

• Bir örnek vermek gerekirse; 2, 4, 4, 4, 5, 7, 9 değerlerine sahip bir örneklemi ele alalım. • Ortalamamız {(2+4+4+4+5+5+7+9)/8} = 5 olacaktır. • Her bir değerin ortalamadan farkını bulup karesini alırız, ve bu kareleri toplayıp toplam gözlem sayısına böler, sonucun kare kökünü alarak standart sapmaya ulaşırız. • (9+1+1+1+0+0+4+16)/8 = 4 ve 4’ün de kare kökü 2’dir. 39

• Puanların her birinden, bu puanların aritmetik ortalaması çıkarılırsa farkları elde edilir. Bu işlemlerde elde edilen fark puanlarına ortalamadan sapmalar denir. Aritmetik ortalamadan sapmaların kareleri alınıp toplanırsa elde edilen sonuca variyans denir. Standart sapma formülündeki karekök kaldırıldığında variyans hesaplanır.

Örneğin: Bir basit yığın için kilogram birimi ile veri (4, 8, 12) olsun. Aritmetik ortalama 8 olur ve verilerin ortalamadan sapmaları (− 4, 0 , 4) olur. Kare toplamlarının ortalaması olan varyans [(4 -8)2+(8 -8)2+(12 -8)2]/3 = 32/3 = 10, 666 olur ve kilogram kare birimi ile verilir. Standart sapma 10, 66’nın karekökü olup 3, 26 değerindedir ve kilogram birimi ile ölçülür. 41

• Standart sapma ve varyans : • Tüm değerlerin dağılımı ile bilgi verirler. Tüm değerler eşitse, her ikisi de sıfıra eşittir. • Değerler arasında farklar arttıkça standart sapma (Ss) ve varyans büyür.

• Standart sapma değişken değerlerinin ortalamanın etrafındaki yayılmasını temsil eden bir yayılma ölçütüdür. Yani, denekler arasında ne kadar yaygınlık olduğunu ifade eder. • Ss’ nın karesine varyans adı verilir. • Merkezi eğilim ölçütü olarak ortalama kullanıldığında, yayılma ölçütü olarak da standart sapma kullanılır.

• Bir dizi puanın varyansı o dizideki değişkenliğin bir ölçüsüdür. Puanların variyansı denildiğinde, puanların değişkenliğinin ölçüsü ifade edilmiş olur. Varyansın karakökü alınırsa standart sapma elde edilir. Varyans standart sapmanın karesi olduğundan , bu istatistiklerden birisi bilindiğinde diğerinin hesaplanması kolaydır.

• Standart sapma, bir merkezi dağılım ölçüsü olarak puanların merkezi yığılma ölçüsünden uzaklıklarının bir ortalama değeri anlamını taşımaktadır. • Bir dizideki ölçümlerin birbirinden farkı arttıkça standart sapma büyür; ölçümler birbirine yaklaştıkça da küçülür.

• Başka bir deyişle, dizideki ölçümlerin dağıldığı alan genişledikçe standart sapma büyür, dağılım alanı küçülüp daraldıkça da küçülür. • Standart sapma küçüldükçe dizi grubundaki homojenlik(benzerlik) artar.

• Standart sapma dağılım ölçüleri arasında en çok kullanılmakta olanıdır. Standart sapmanın da bir ortalama olduğunu hatırlatmak gerekir. (Ortalamadan olan farkların ortalaması)

• Dağılımın yaygınlığını gösteren ölçümlerin en önemlisi varyansdır. Eğer varyans küçükse sayılar birbirine yakın, büyükse daha uzaktır. • Standart sapma büyüdükçe dağılım yaygınlaşır.

• Aritmetik ortalamaları aynı olan iki dağılım aynı yaygınlıkta olmayabilir. • Örneğin; 10, 22, 34 değerlerini alan 3 kişilik bir dağılımda aritmetik ortalama 66/3=22’dir. 21, 23, 22 değerlerini alan başka bir 3 kişilik dağılımda aritmetik ortalama yine 66/3=22’dir.

• İki dağılımın aritmetik ortalaması 22 olduğu halde birinci dağılımda değerler (1 ve 3’üncü değerler) aritmetik ortalamadan çok uzakta iken ikinci dağılımdaki değerler ortalamaya çok yakındır. • Bir dağılımda değerler aritmetik ortalamadan uzaklaştıkça dağılımın yaygınlığı artar.

• Genel olarak, standart sapmanın küçük olması; ortalamadan sapmaların ve riskin az olduğunun, büyük olması ise; ortalamadan sapmaların, riskin çok olduğunun ve oynaklığın göstergesidir.

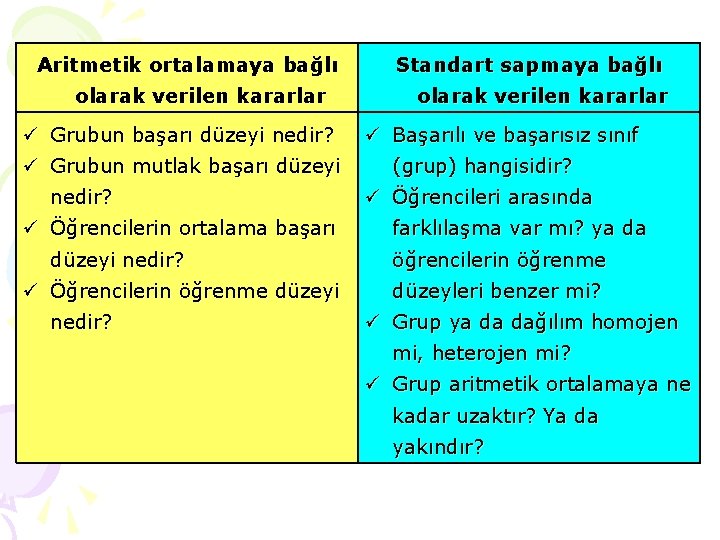
Aritmetik ortalamaya bağlı olarak verilen kararlar Standart sapmaya bağlı olarak verilen kararlar Grubun başarı düzeyi nedir? Başarılı ve başarısız sınıf Grubun mutlak başarı düzeyi (grup) hangisidir? nedir? Öğrencileri arasında Öğrencilerin ortalama başarı farklılaşma var mı? ya da düzeyi nedir? öğrencilerin öğrenme Öğrencilerin öğrenme düzeyi düzeyleri benzer mi? nedir? Grup ya da dağılım homojen mi, heterojen mi? Grup aritmetik ortalamaya ne kadar uzaktır? Ya da yakındır?

VARYASYON KATSAYISI (DEĞİŞİM KATSAYISI) Standart sapma dağılımın yaygınlığını gösteren bir ölçüdür. Ancak standart sapma ile dağılım hakkında çok fazla bir şey söylemek olanaksızdır. Örneğin; bir dağılımın standart sapması 6 ise bu değer büyük müdür, yoksa küçük müdür?

• Bir karar verebilmek için VARYASYON KATSAYISINI hesaplamak gerekir. • Varyasyon katsayısı; standart sapmanın ortalamaya göre yüzde kaçlık bir değişim gösterdiğini belirtir. S V = ----- x 100 X

Örnek : Ortalaması 31. 7 ve standart sapması 8. 37 olan bir dağılımın varyasyon katsayısı, V = (8. 37 / 31. 7) x 100 = % 26. 4 Bu dağılımdaki değerler ortalamaya göre %26. 4’lük bir değişim göstermektedir.

• Standart sapma, eğitimde başarıyı belirlemede ortalamalar ile birlikte yaygın bir şekilde kullanılmaktadır. Eğer bir sınavda grup ortalamaları eşit ise standart sapması daha küçük olan grup daha başarılıdır. Standart sapması küçük olan gruplarda öğrencilerin öğrenme düzeyleri daha birbirine yakın iken, standart sapması büyük olan gruplarda öğrenme düzeyleri arasında daha belirgin farklar mevcuttur. • Bir dağılımda değerler aritmetik ortalamadan uzaklaştıkça dağılımın yaygınlığı artar. • Standart sapmanın küçüklüğü; ortalamaya yakınlığı, büyüklüğü ise; ortalamaya uzaklığı ifade eder. 56

Standart Sapma ve Aritmetik Ortalama Arasındaki İlişki Aritmetik ortalama ile standart Heterojen yapı oluşur ve grup sapmanın arası büyürse, başarısı düşer. Aritmetik ortalama ile standart Homojen yapı oluşur ve grup sapmanın arası küçülürse, başarısı artar. Bir puan dağılımında puanlar Standart sapmada büyür. arası fark (ranj) büyüdükçe, Bir testten elde edilen puanların standart sapması büyüdükçe, Testin güvenirliği artar (Standart hata formülünü inceleyiniz) Se= Ölçmenin standart hatası Sx= Test puanlarının standart sapması rx = Testin güvenirliği

Çarpıklık ve Basıklık Ölçüleri Çarpıklık(Skewness) • Çarpıklık, normal dağılışta simetrikliğin bozulma derecesidir. Dağılış sağa uzun kuyruklu ise pozitif çarpık veya sağa çarpık, dağılış sola uzun kuyruklu ise negatif çarpık vaya sola çarpık olarak adlandırılır. Basıklık(Kurtosis) • Normal dağılış eğrisinin sivrilik veya yayvanlık derecesi basıklık olarak adlandırılır.

Dağılım şekli ölçütleri • Ortalama=ortanca=mod ise dağılım normal dağılımdır. • Çarpıklık (skewness): Mod<ortanca<ortalama ise dağılım sağdan çarpık; ortalama<ortanca<mod ise dağılım soldan çarpıktır. • Sivrilik-basıklık (kurtosis): Eğrinin tepesi sivriyse dağılım leptokurtik; tepesi basıksa dağılım platikurtiktir.

Grafiklerin Yorumlanması(Aritmetik ortalama, mod, medyan ilişkisi) • Uygulanan bir testin aritmetik ortalaması, modu, medyanı ve standart sapması bulunduktan sonra bunun nasıl bir dağılım gösterdiğini ortaya koymak gerekir. Grafiklerin yorumlanması ile grubun başarı durumu hakkında bilgi edinilebilir.

Normal(simetrik)Dağılım • Başarı açısından normal düzeyde olan bir sınıfın grafiğidir. Normal dağılım eğrisi genelde çan biçiminde olur. • Aritmetik ortalama, mod ve medyan değerleri aynıysa bu dağılım simetriklik gösterir.

1. Simetrik dağılışlarda bu üç değer birbirine eşittir. (A. O. = Medyan = Mod)

0 Ortanca A. Ortalama MERKEZİ EĞİLİM ÖLÇÜLERİ 50 Normal dağılım 100

2. Sola çarpık dağılışlarda aritmetik ortalama ortancadan, ortanca ise tepe değerinden daha küçüktür. (A. O. Medyan Mod)

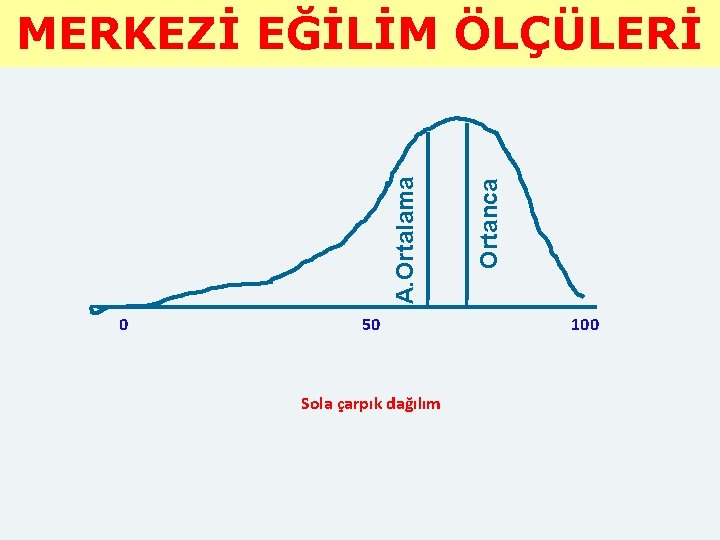
0 50 Sola çarpık dağılım Ortanca A. Ortalama MERKEZİ EĞİLİM ÖLÇÜLERİ 100

Sola Çarpık(kayışlı)dağılım • Başarı yüksektir. • Öğretim yeterlidir. • Sorular ve test kolaydır. • Puanların çoğu dağılımın sağında toplanmıştır. • Öğrenciler hedef davranışları kazanmışlardır.

3. Sağa çarpık dağılışlarda aritmetik ortalama ortancadan, ortanca ise tepe değerinden daha büyüktür. (A. O. Medyan Mod)

0 A. Ortalama Ortanca MERKEZİ EĞİLİM ÖLÇÜLERİ 50 Sağa çarpık dağılım 100

Sağa Çarpık(Kayışlı) dağılım • Başarı düşüktür. • Öğretme yetersizdir. • Test zordur. • Puanların çoğu sol tarafa yığılmıştır. • Öğrenme düzeyi düşüktür. • Öğrenciler hedef-davranışları kazamamışlardır.

Sorular • 1, 5, 5, 4, 6, 2, 2, 1, 2, 5, 5, 6, 5 veri değerlerine sahip 15 gözlemli bir örneklemin modu nedir? – Cevap: 5 • 2, 6, 8, 10 dizisinin medyanı nedir? – Cevap: (6+8)/2 = 7 • 10, 25, 30, 15, 5, 7 örnekleminin aritmetik ortalaması nedir? – Cevap: (10+10+25+30+15+5+7)/6 = 17 70

Sorular • Değerleri 2, 4, 6 olan bir örneklemin standart sapması nedir? Cevap: – önce ortalamayı buluruz: (2+4+6)/3 = 4 – her değerin farklar karesini buluruz: (2 -4)2 = 4 (4 -4)2 = 0 (6 -4)2 = 4 – bunları toplar ve toplam gözlem sayısına bölüp karekökünü alırız, bu da bize standart sapmayı verir: (4+0+4)/3 = 2, 66 ve 2, 66’nın karekökü ise 1, 63’tür. – standart sapma 1, 63’tür. 71

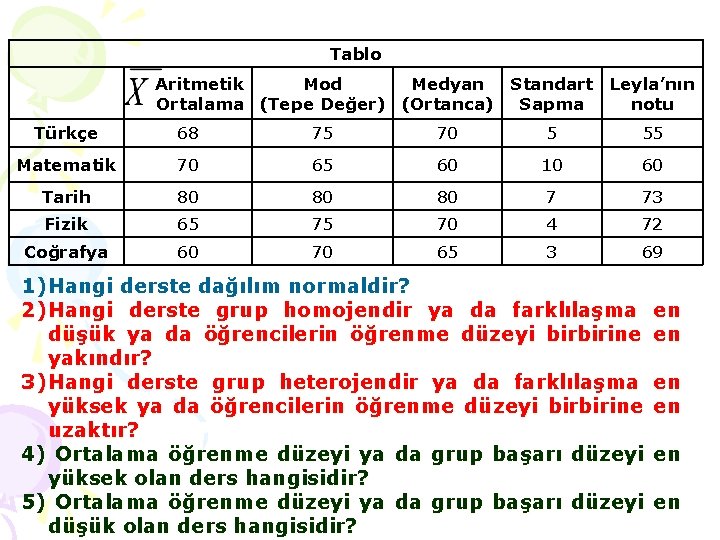
Tablo Aritmetik Mod Medyan Standart Leyla’nın Ortalama (Tepe Değer) (Ortanca) Sapma notu Türkçe 68 75 70 5 55 Matematik 70 65 60 10 60 Tarih 80 80 80 7 73 Fizik 65 75 70 4 72 Coğrafya 60 70 65 3 69 1) Hangi derste dağılım normaldir? 2) Hangi derste grup homojendir ya da farklılaşma düşük ya da öğrencilerin öğrenme düzeyi birbirine yakındır? 3) Hangi derste grup heterojendir ya da farklılaşma yüksek ya da öğrencilerin öğrenme düzeyi birbirine uzaktır? 4) Ortalama öğrenme düzeyi ya da grup başarı düzeyi yüksek olan ders hangisidir? 5) Ortalama öğrenme düzeyi ya da grup başarı düzeyi düşük olan ders hangisidir? en en en

Kaynaklar • • • Arıkan, R. , 2007. Araştırma Teknikleri ve Rapor hazırlama. Asil Yayın Dağ, Ankara. Nazik, H. , Arlı, M. , 2004. Bilimsel Araştırmaya Giriş. Gazi Kitabevi Kaptan, S. , 1998. Bilimsel Araştırma ve İstatistik Teknikleri. Tekışık web ofset, Ankara. Yıldız, N. , Akbulut, Ö. , Bircan, H. , 2002. İstatistiğe Giriş. Aktif Yayınevi, Erzurum Ercan, M. , 1997. Bilimsel Araştırmalarda İstatistik. İzmit. Türkbal, A. , 1987. Bilimsel Araştırma Metodları ve Uygulamalı İstatistik. Atatürk Üniversitesi Basımevi, Erzurum. www. egitim. aku. edu. tr www. hocaman. net/index_dosyalar/ÖLÇME 111. ppt www. iibf. ibu. edu. tr/stratejikplanlama/kamuyonetimibolumu. www. yildiz. edu. tr/~tuzkaya/MIG_Ders_Notlari/sunum_ www. muhasebat. gov. tr/. . . /S. 4. %20 MALİ%20İSTATİSTİK. Science. ankara. edu. tr/Özdemir/istatistik

• • • Kahyaoğlu, M. , (2009)”Ögretmen Adaylarının Fen ve Teknoloji Dersinde Çevresel Problemlerin Ögretimine Yönelik Bakıs Açıları, Hazır Bulunuslukları ve Öz-Yeterliliklerinin Belirlenmesi “, Mehmet Akif Ersoy Üniversitesi Egitim Fakültesi Dergisi, Yıl 9, Sayı 17, 28 - 40. Yin, Y. , Vandeles, J, . A Comparison of Two Construct-a-Concept-Map Science Assessments: Created Linking Phrases and Selected Linking Phrases CSE Report 624 National Center for Research on Evaluation, Standards, and Student Testing (CRESST)/Stanford University Blake, A. , (2004)”Helping young children to see what is relevant and why: supporting cognitive change in earth science using analogy “ınt. J. SCI. EDUC. , , vol. 26, NO. 15, 1855– 1873. Dindar, H. , Yangın, S. (2007)”İlköğretim Fen ve Teknoloji Dersi Öğretim Programına Geçiş Sürecinde Öğretmenlerin Bakış Açılarının Değerlendirilmesi” , Cilt: 15 No: 1 Kastamonu Eğitim Dergisi 185 -198. Yenice, N. , Balım, A. , Aydın, G. , (2008)”Biyoloji Öğretmenlerinin Laboratuvar Dersine Yönelik Tutumlar ve Teknolojik Yenilikleri İzleme Eğilimleri “, Cilt: 16 No: 2 Kastamonu Eğitim Dergisi , 469 -484.