Merging Probability Distributions from Various Types of Geoscience

Merging Probability Distributions from Various Types of Geoscience Information Oktay Erten and Clayton V. Deutsch

Presentation Outline • The importance of secondary information • Second-order stationarity assumption • Generation of the synthetic data including primary and secondary variables • Constructing the conditional distribution of the primary variable given both the samples of the secondary and primary variables • Merging the independent univariate or multivariate distributions through the error ellipse method 2

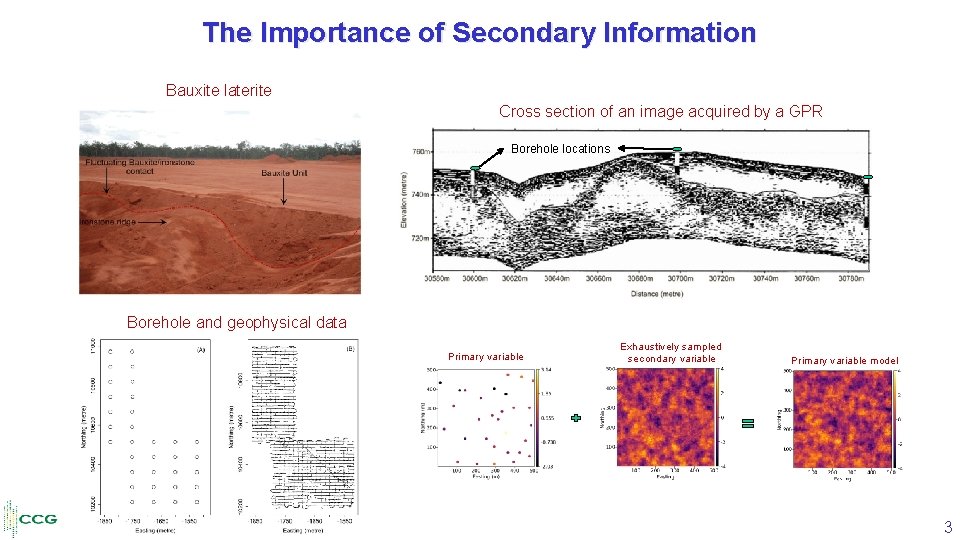
The Importance of Secondary Information Bauxite laterite Cross section of an image acquired by a GPR Borehole locations Borehole and geophysical data Primary variable Exhaustively sampled secondary variable Primary variable model 3

Stationarity • (1) (2) (3) (4) (5) (6) 4

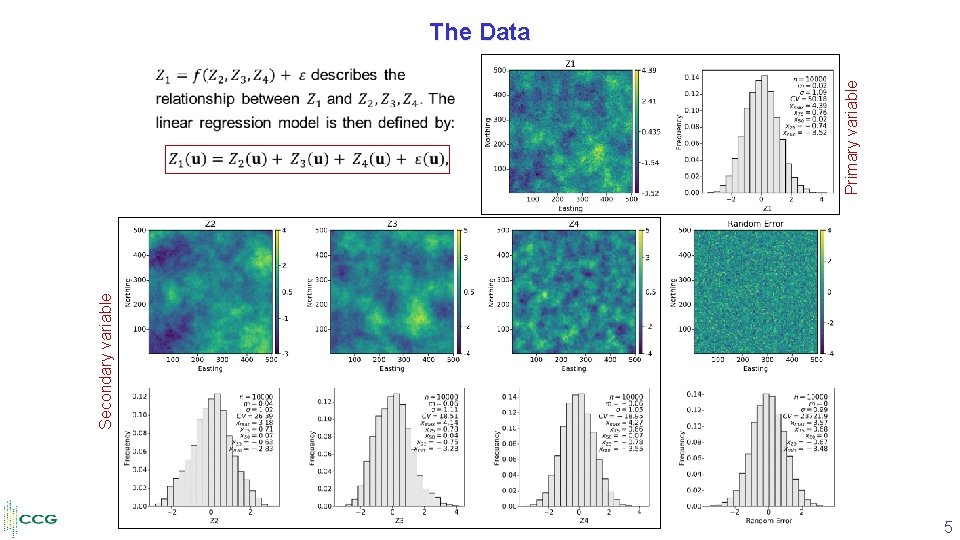
Secondary variable • Primary variable The Data 5

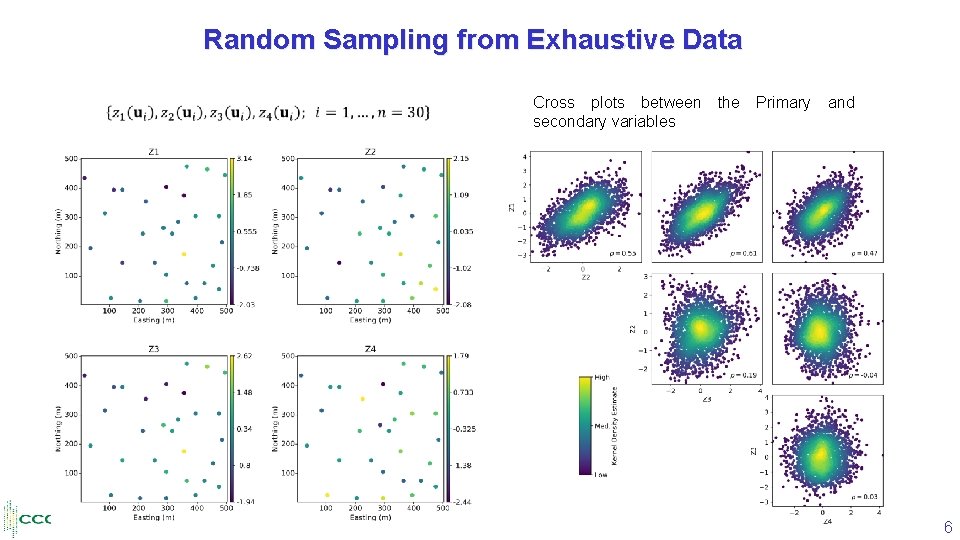
Random Sampling from Exhaustive Data Cross plots between secondary variables the Primary and 6

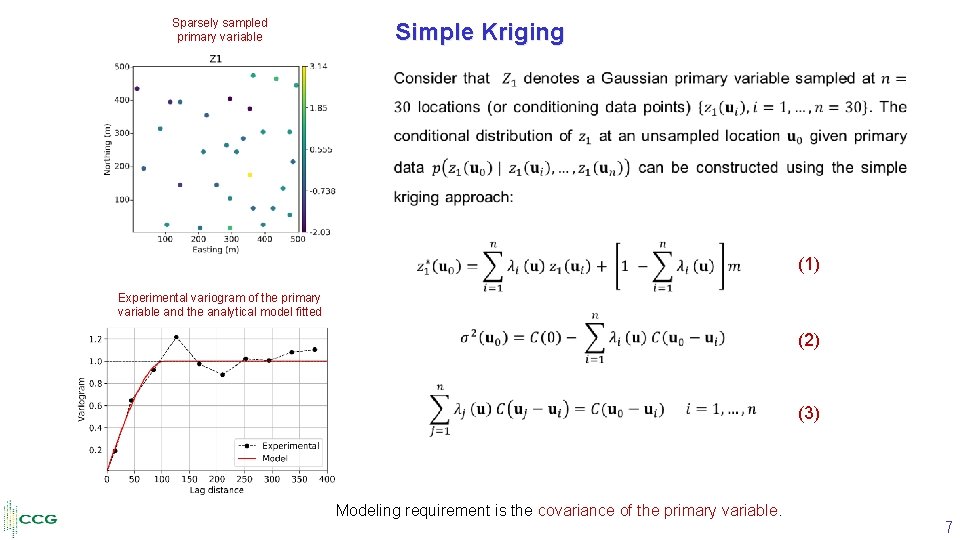
Sparsely sampled primary variable Simple Kriging • (1) Experimental variogram of the primary variable and the analytical model fitted (2) (3) Modeling requirement is the covariance of the primary variable. 7

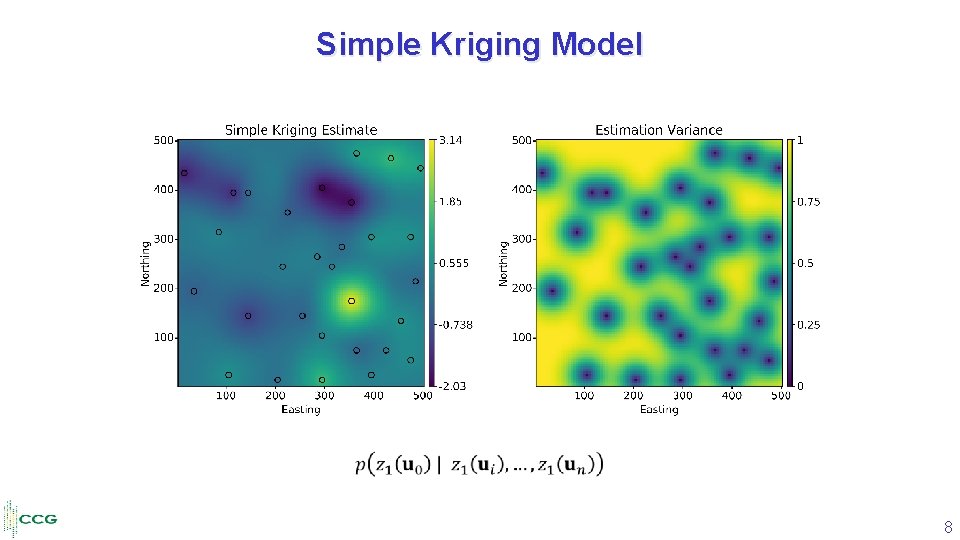
Simple Kriging Model 8

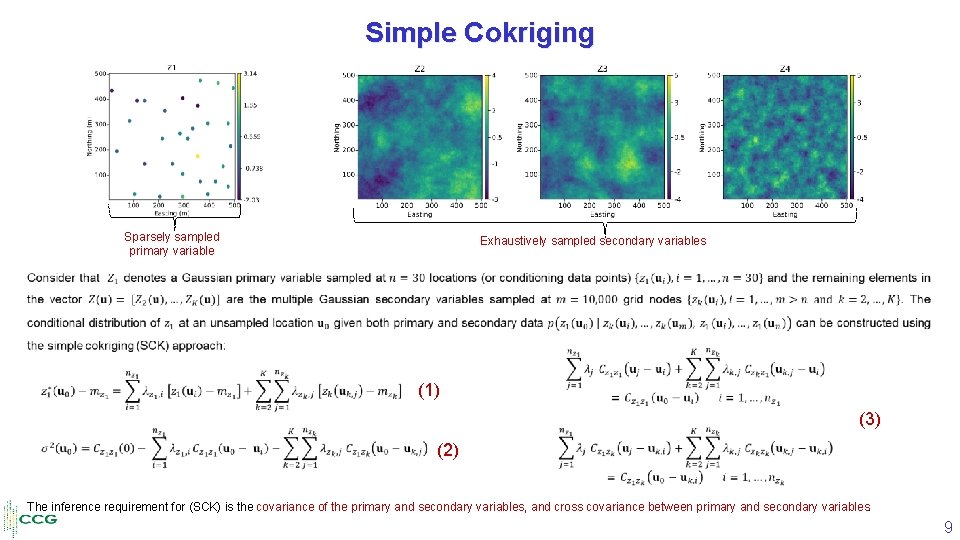
Simple Cokriging Sparsely sampled primary variable Exhaustively sampled secondary variables • (1) (3) (2) The inference requirement for (SCK) is the covariance of the primary and secondary variables, and cross covariance between primary and secondary variables. 9

Linear Model of Coregionalization • 10

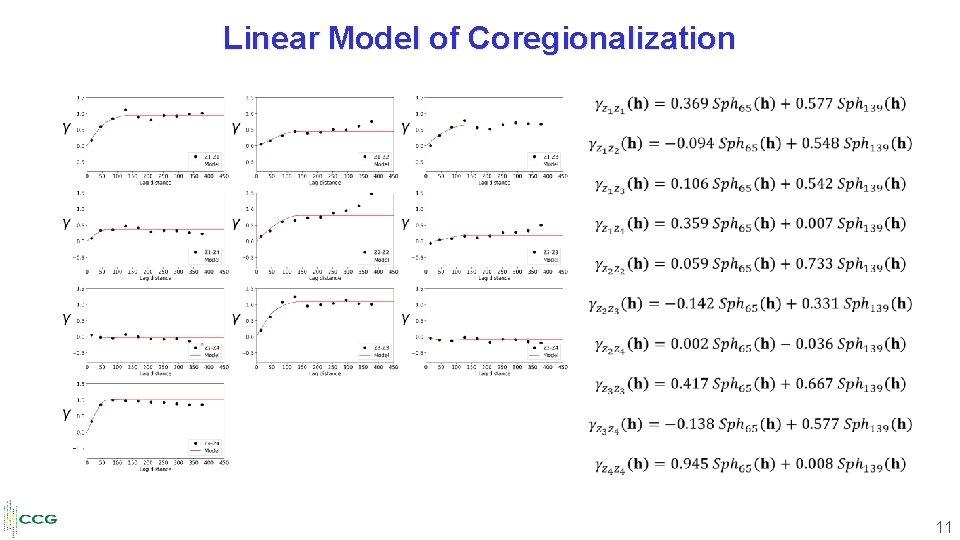
Linear Model of Coregionalization 11

Simple Cokriging Model 12

Collocated Simple Cokriging Isotropic neighborhood Sparsely sampled primary variable Exhaustively sampled secondary variables (1) (3) (2) The inference requirement for SCCK is the covariance of the primary variable. 13

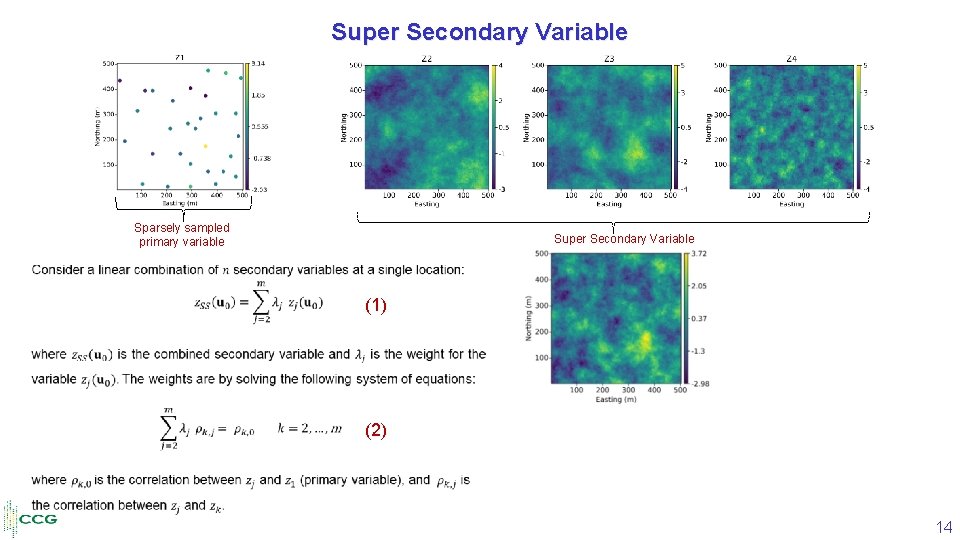
Super Secondary Variable Sparsely sampled primary variable Super Secondary Variable (1) (2) 14

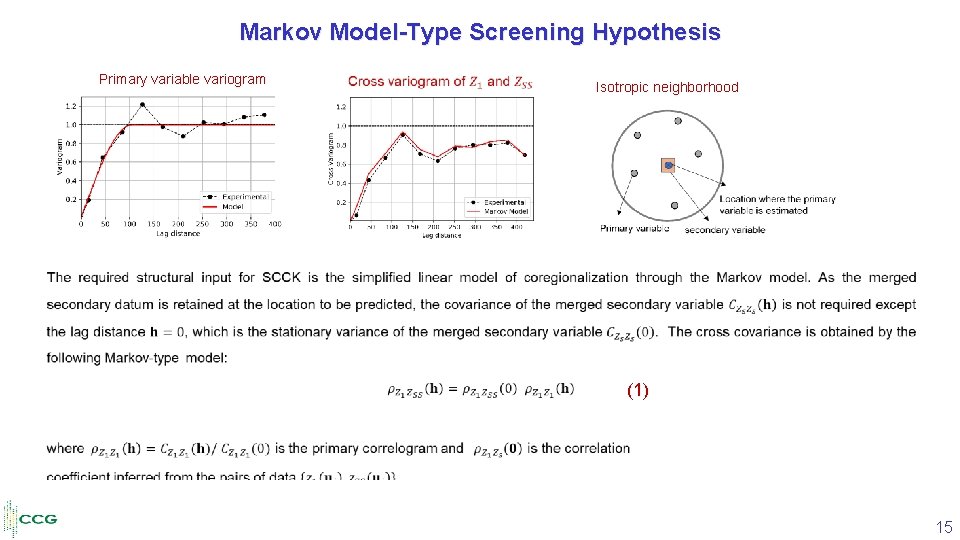
Markov Model-Type Screening Hypothesis Primary variable variogram Isotropic neighborhood • (1) 15

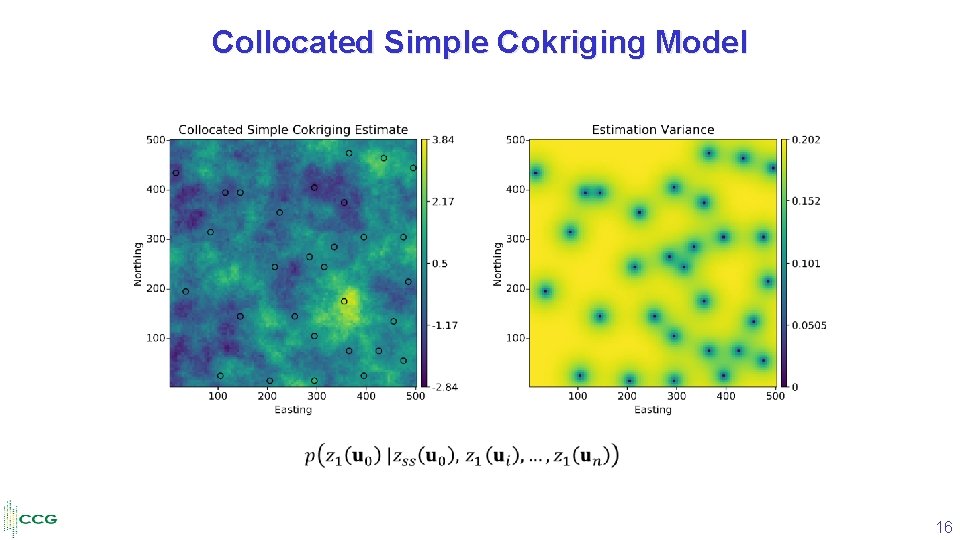
Collocated Simple Cokriging Model 16

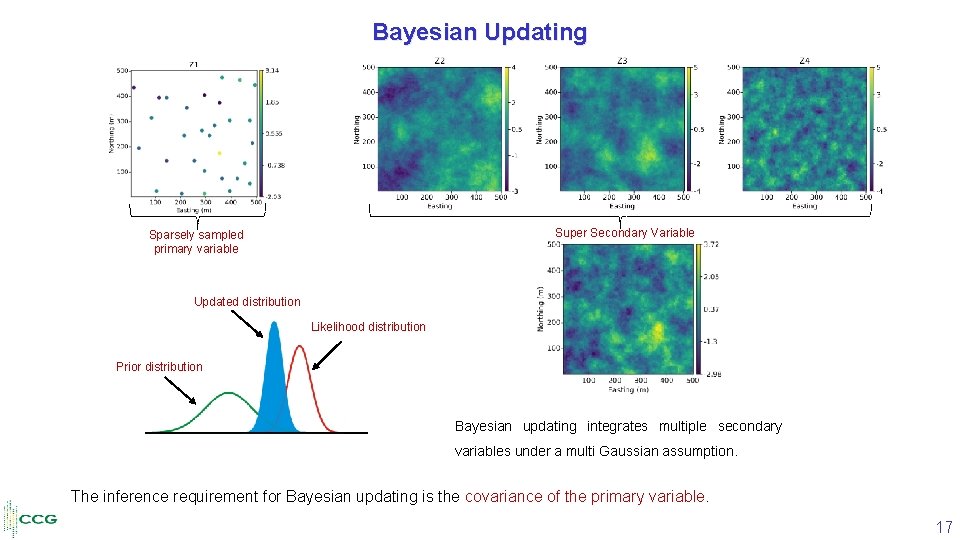
Bayesian Updating Super Secondary Variable Sparsely sampled primary variable Updated distribution Likelihood distribution Prior distribution Bayesian updating integrates multiple secondary variables under a multi Gaussian assumption. The inference requirement for Bayesian updating is the covariance of the primary variable. 17

Bayesian Updating Conditional distribution of the primary variable 18

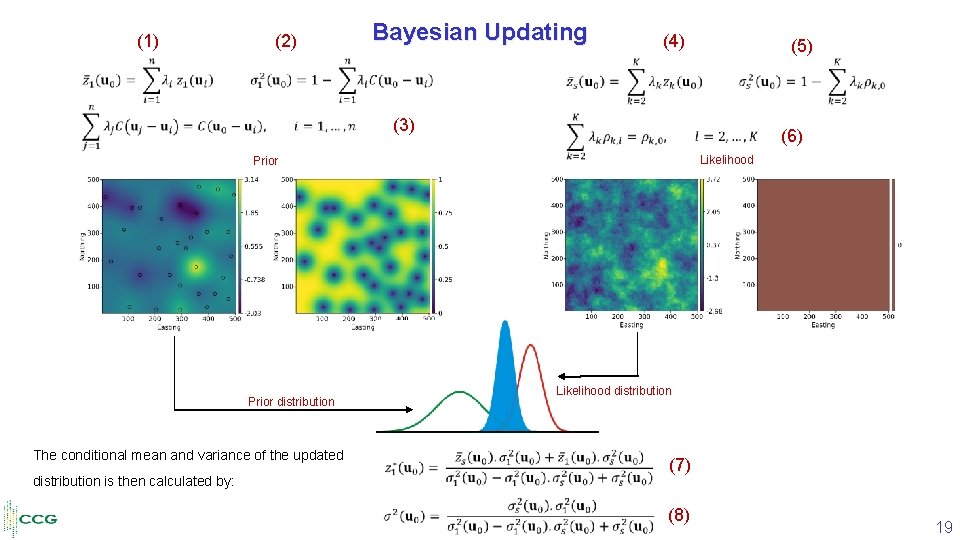
(1) (2) Bayesian Updating (4) (5) (3) (6) Likelihood Prior distribution The conditional mean and variance of the updated distribution is then calculated by: Likelihood distribution (7) (8) 19

Bayesian Updating 20

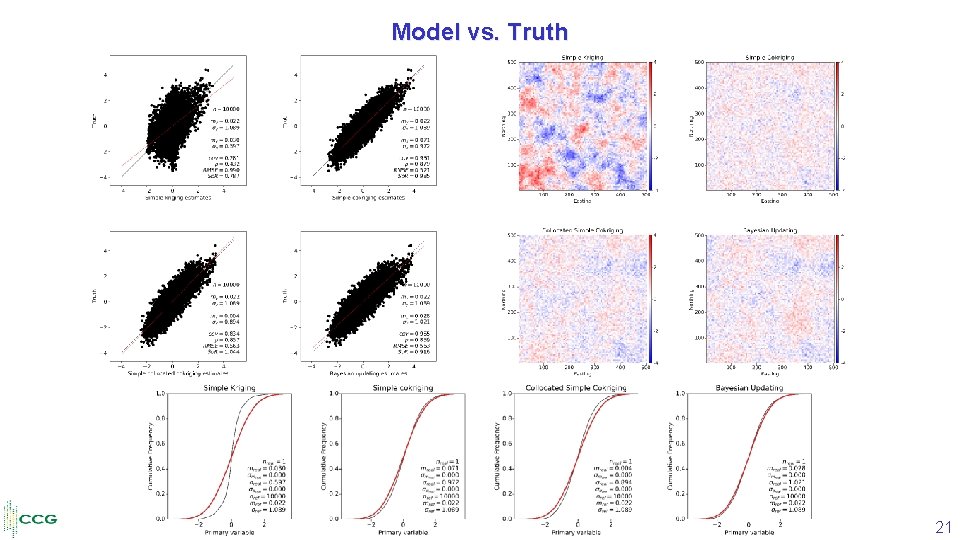
Model vs. Truth 21

Error Ellipse (1) (2) 22

Error Ellipse • Methodology: (Rezvandehy, 2016). 1 - The variances of each Gaussian lag distribution are obtained through the variogram uncertainty calculated for each lag 2 - The mean of each Gaussian lag distribution comes from the analytical model fitted to the experimental variograms. 3 - Modify the variance of the secondary variable based on the crossvariogram between the primary and secondary variables. 4 - Calculate the updated variogram Rezvandehy, M. (2016). Geostatistical reservoir modeling with parameter uncertainty in presence of limited well data (Ph. D thesis). University of Alberta, Edmonton, Canada. 23

Conclusions • We have presented some available techniques where the probability distributions from different sources of information are merged • In simple cokriging, the conditional distributions are computed from the parameterized high dimensional distributions • In simple collocated cokriging and Bayesian updating, a known prior distribution is considered and the neutral assumption is made in relation to the redundancy in the information content, i. e. Markov‐type (screening) hypothesis • In error ellipse, there is no clear prior distribution and the conditional independence is assumed in the likelihood distributions. 24

Thank you! Questions? 25