Merge sort Insertion sort Sorting I Slide 2

Merge sort, Insertion sort

Sorting I / Slide 2 Sorting * Selection sort or bubble sort 1. 2. 3. * * * * Find the minimum value in the list Swap it with the value in the first position Repeat the steps above for remainder of the list (starting at the second position) Insertion sort Merge sort Quicksort Shellsort Heapsort Topological sort …

Sorting I / Slide 3 Bubble sort and analysis for (i=0; i<n-1; i++) { for (j=0; j<n-1 -i; j++) { if (a[j+1] < a[j]) { // compare the two neighbors tmp = a[j]; // swap a[j] and a[j+1] a[j] = a[j+1]; a[j+1] = tmp; } } } * Worst-case analysis: N+N-1+ …+1= N(N+1)/2, so O(N^2)

Sorting I / Slide 4 *Mergesort: n Divide and conquer principle *Insertion: n Incremental algorithm principle

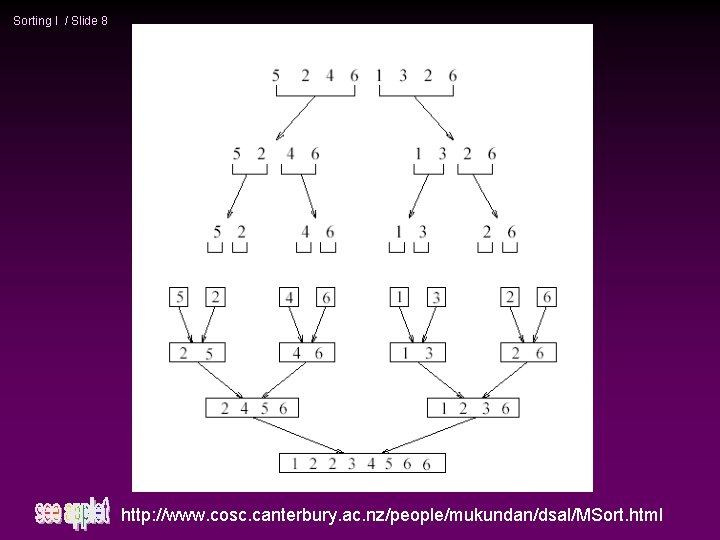
Sorting I / Slide 5 Mergesort Based on divide-and-conquer strategy Divide the list into two smaller lists of about equal sizes * Sort each smaller list recursively * Merge the two sorted lists to get one sorted list * How do we divide the list? How much time needed? How do we merge the two sorted lists? How much time needed?

Sorting I / Slide 6 Dividing * If an array A[0. . N-1]: dividing takes O(1) time n we can represent a sublist by two integers left and right: to divide A[left. . Right], we compute center=(left+right)/2 and obtain A[left. . Center] and A[center+1. . Right]

Sorting I / Slide 7 Mergesort * Divide-and-conquer strategy recursively mergesort the first half and the second half n merge the two sorted halves together n

Sorting I / Slide 8 http: //www. cosc. canterbury. ac. nz/people/mukundan/dsal/MSort. html

Sorting I / Slide 9 How to merge? Input: two sorted array A and B * Output: an output sorted array C * Three counters: Actr, Bctr, and Cctr * n initially set to the beginning of their respective arrays (1) The smaller of A[Actr] and B[Bctr] is copied to the next entry in C, and the appropriate counters are advanced (2) When either input list is exhausted, the remainder of the other list is copied to C

Sorting I / Slide 10 Example: Merge

Sorting I / Slide 11 Example: Merge. . . *Running time analysis: n Clearly, merge takes O(m 1 + m 2) where m 1 and m 2 are the sizes of the two sublists. *Space requirement: nmerging two sorted lists requires linear extra memory nadditional work to copy to the temporary array and back

Sorting I / Slide 12

Sorting I / Slide 13 Analysis of mergesort Let T(N) denote the worst-case running time of mergesort to sort N numbers. Assume that N is a power of 2. Divide step: O(1) time * Conquer step: 2 T(N/2) time * Combine step: O(N) time Recurrence equation: * T(1) = 1 T(N) = 2 T(N/2) + N

Sorting I / Slide 14 Analysis: solving recurrence Since N=2 k, we have k=log 2 n

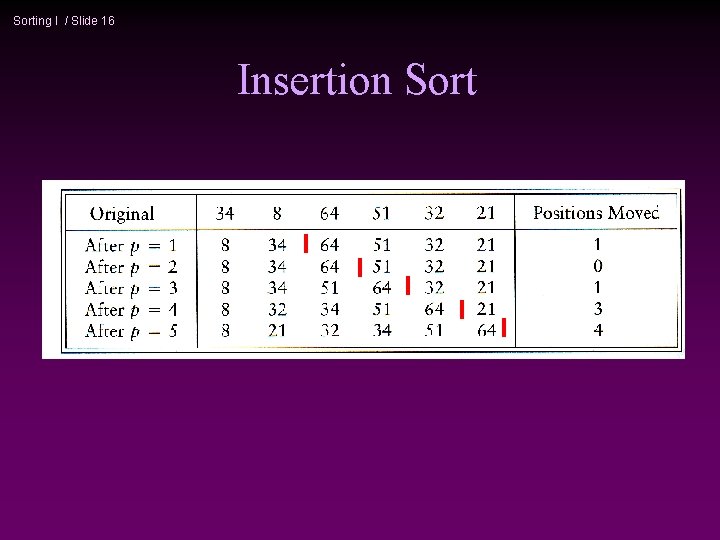
Sorting I / Slide 15 Insertion sort 1) Initially p = 1 2) Let the first p elements be sorted. 3) Insert the (p+1)th element properly in the list (go inversely from right to left) so that now p+1 elements are sorted. 4) increment p and go to step (3)

Sorting I / Slide 16 Insertion Sort

Sorting I / Slide 17 Insertion Sort http: //www. cis. upenn. edu/~matuszek/cse 121 -2003/Applets/Chap 03/Insertion/Insert. Sort. html * * Consists of N - 1 passes For pass p = 1 through N - 1, ensures that the elements in positions 0 through p are in sorted order elements in positions 0 through p - 1 are already sorted n move the element in position p left until its correct place is found among the first p + 1 elements n

Sorting I / Slide 18 Extended Example To sort the following numbers in increasing order: 34 8 64 51 32 21 p = 1; tmp = 8; 34 > tmp, so second element a[1] is set to 34: {8, 34}… We have reached the front of the list. Thus, 1 st position a[0] = tmp=8 After 1 st pass: 8 34 64 51 32 21 (first 2 elements are sorted)

Sorting I / Slide 19 P = 2; tmp = 64; 34 < 64, so stop at 3 rd position and set 3 rd position = 64 After 2 nd pass: 8 34 64 51 32 21 (first 3 elements are sorted) P = 3; tmp = 51; 51 < 64, so we have 8 34 64 32 21, 34 < 51, so stop at 2 nd position, set 3 rd position = tmp, After 3 rd pass: 8 34 51 64 32 21 (first 4 elements are sorted) P = 4; tmp = 32, 32 < 64, so 8 34 51 64 64 21, 32 < 51, so 8 34 51 51 64 21, next 32 < 34, so 8 34 34, 51 64 21, next 32 > 8, so stop at 1 st position and set 2 nd position = 32, After 4 th pass: 8 32 34 51 64 21 P = 5; tmp = 21, . . . After 5 th pass: 8 21 32 34 51 64

Sorting I / Slide 20 Analysis: worst-case running time Inner loop is executed p times, for each p=1. . N Overall: 1 + 2 + 3 +. . . + N = O(N 2) * Space requirement is O(N) *

Sorting I / Slide 21 The bound is tight (N 2) * That is, there exists some input which actually uses (N 2) time * Consider input as a reversed sorted list n When a[p] is inserted into the sorted a[0. . p-1], we need to compare a[p] with all elements in a[0. . p-1] and move each element one position to the right (i) steps * n the total number of steps is ( 1 N-1 i) = (N(N-1)/2) = (N 2)

Sorting I / Slide 22 Analysis: best case * The input is already sorted in increasing order When inserting A[p] into the sorted A[0. . p-1], only need to compare A[p] with A[p-1] and there is no data movement n For each iteration of the outer for-loop, the inner for -loop terminates after checking the loop condition once => O(N) time n * If input is nearly sorted, insertion sort runs fast

Sorting I / Slide 23 Summary on insertion sort * * * * Simple to implement Efficient on (quite) small data sets Efficient on data sets which are already substantially sorted More efficient in practice than most other simple O(n 2) algorithms such as selection sort or bubble sort: it is linear in the best case Stable (does not change the relative order of elements with equal keys) In-place (only requires a constant amount O(1) of extra memory space) It is an online algorithm, in that it can sort a list as it receives it.

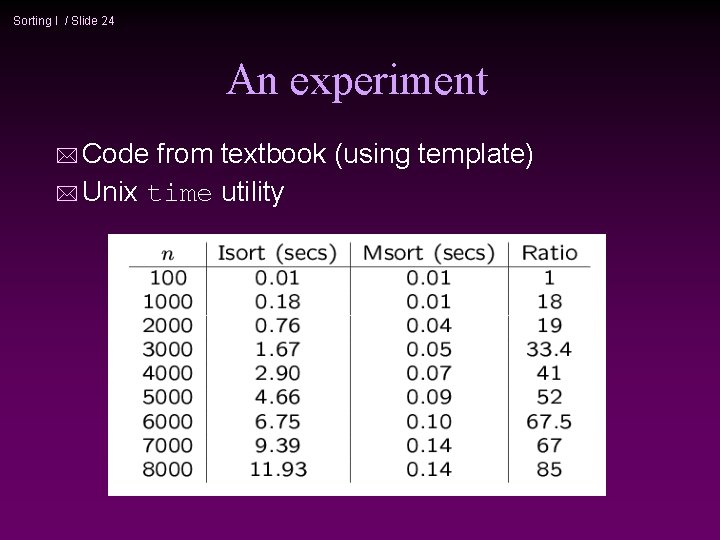
Sorting I / Slide 24 An experiment * Code from textbook (using template) * Unix time utility

Sorting I / Slide 25