Merge sort Algorithm Analysis January 31 2020 Cinda

Merge sort Algorithm Analysis January 31, 2020 Cinda Heeren / Andy Roth / Geoffrey Tien 1

Mergesort introduction • Merge sort is an efficient sorting algorithm – Divide and conquer – Divides an array in half, and merges the two sorted halves • Sorting happens during the merge step January 31, 2020 Cinda Heeren / Andy Roth / Geoffrey Tien 2

Subarray merging of two sorted subarrays 1 4 8 1 January 31, 2020 3 3 4 5 7 8 Cinda Heeren / Andy Roth / Geoffrey Tien 3

Getting sorted subarrays • Repeatedly divide arrays in half until each subarray contains a single element – an element by itself is already sorted – merging two single-element arrays is simply a single comparison • The merge step copies the subarray halves into a temporary array – and the merged elements are copied from the temporary array back to the original array January 31, 2020 Cinda Heeren / Andy Roth / Geoffrey Tien 4

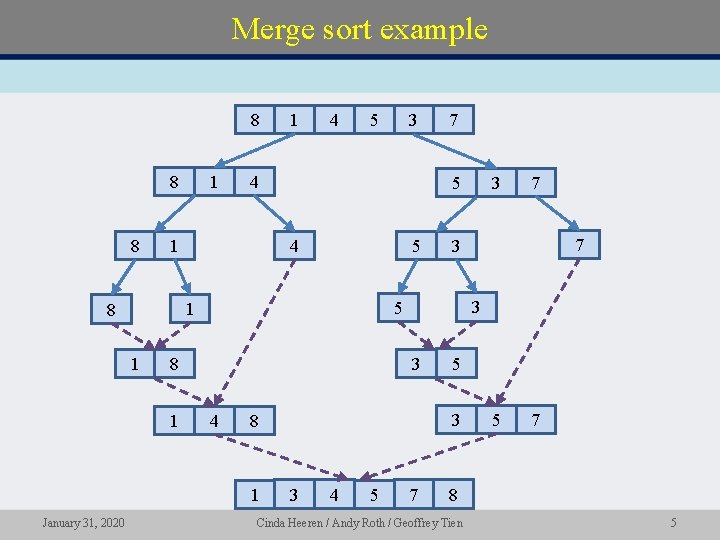
Merge sort example 8 1 8 8 4 5 3 4 5 7 5 3 8 1 7 3 3 4 3 3 5 8 1 7 5 1 1 3 4 1 8 January 31, 2020 1 7 5 7 8 Cinda Heeren / Andy Roth / Geoffrey Tien 5

Recursive Merge sort void Merge. Sort(int[] arr, int low, int high) { if (low < high) // array has more than 1 element { int mid = low + (high – low) / 2; // sort the left half Merge. Sort(arr, low, mid); // sort the right half Merge. Sort(arr, mid+1, high); low 1 high mid 4 8 3 5 7 // Merge the sorted halves Merge(arr, low, mid, high); } } January 31, 2020 The actual sorting work is done by Merge! Exercise: think about how to write Merge (iteratively) Cinda Heeren / Andy Roth / Geoffrey Tien 6

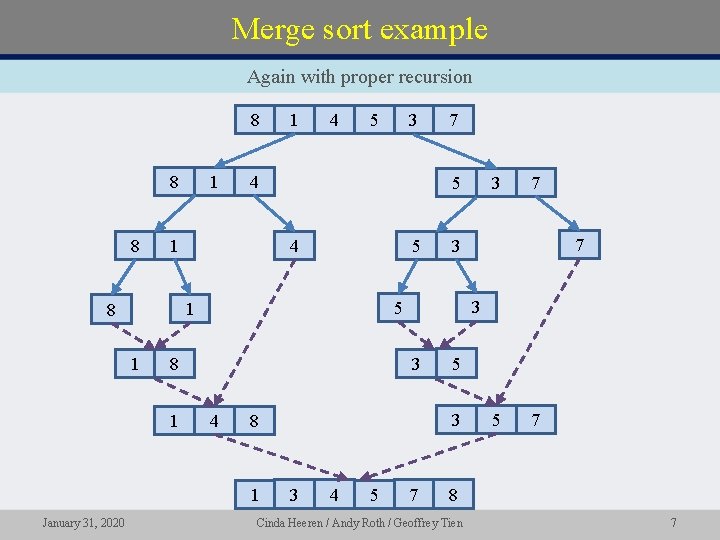
Merge sort example Again with proper recursion 8 1 8 8 4 5 3 4 5 7 5 3 8 1 7 3 3 4 3 3 5 8 1 7 5 1 1 3 4 1 8 January 31, 2020 1 7 5 7 8 Cinda Heeren / Andy Roth / Geoffrey Tien 7

Merge sort analysis Quick & dirty version (recursion tree) • January 31, 2020 Cinda Heeren / Andy Roth / Geoffrey Tien 8

Recurrence relations January 31, 2020 Cinda Heeren / Andy Roth / Geoffrey Tien 9

Analyzing recursive functions • January 31, 2020 Cinda Heeren / Andy Roth / Geoffrey Tien 10

Recurrence relations Example: Recursive max in an array double arr. Max(double arr[], int size, int start) { if (start == sz – 1) return arr[start]; else return max( arr[start], arr. Max(arr, size, start + 1) ); } • January 31, 2020 Cinda Heeren / Andy Roth / Geoffrey Tien 11

Merge sort analysis Now with more math! • January 31, 2020 Cinda Heeren / Andy Roth / Geoffrey Tien 12

In the numeric domain Solving for exact closed forms • January 31, 2020 Cinda Heeren / Andy Roth / Geoffrey Tien 13

Detour – back to sorting Lower bounds on worst case • The big question: Is it possible for a comparison-based sorting algorithm to have better asymptotic worst-case performance than Merge sort? January 31, 2020 Cinda Heeren / Andy Roth / Geoffrey Tien 14

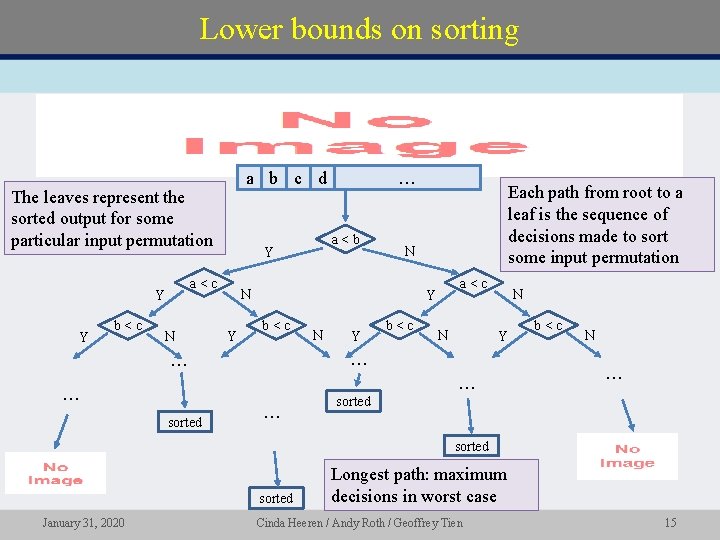
Lower bounds on sorting • a b c d The leaves represent the sorted output for some particular input permutation Y b<c N a<b Y a<c Y … N N Y Each path from root to a leaf is the sequence of decisions made to sort some input permutation a<c Y b<c N N Y … … sorted … b<c N … sorted January 31, 2020 Longest path: maximum decisions in worst case Cinda Heeren / Andy Roth / Geoffrey Tien 15

Lower bounds on sorting Decision tree model • January 31, 2020 Cinda Heeren / Andy Roth / Geoffrey Tien 16

Lower bounds on sorting Height of a perfect decision tree • The longest decision path can be no shorter than this But – there are non-comparison-based sorting algorithms that can perform better (with assumptions). Stay tuned in CPSC 320 (maybe)! January 31, 2020 Cinda Heeren / Andy Roth / Geoffrey Tien 17

Readings for this lesson • Epp: – Chapter 5. 6 – 5. 7 (Recurrence relations) • Next class: – Carrano & Henry: Chapter 15. 1 – 15. 2 (Tree terminology, binary trees & traversals) January 31, 2020 Cinda Heeren / Andy Roth / Geoffrey Tien 18