MENU UTAMA MATRIKS 01 MATRIKS 02 SOAL LATIHAN

MENU UTAMA MATRIKS 01 MATRIKS 02 SOAL LATIHAN

MATRIKS 01

PENDAHULUAN Setelah menyaksikan tayangan ini anda dapat menentukan penyelesaian suatu persamaan matrik dengan menggunakan sifat dan operasi matrik

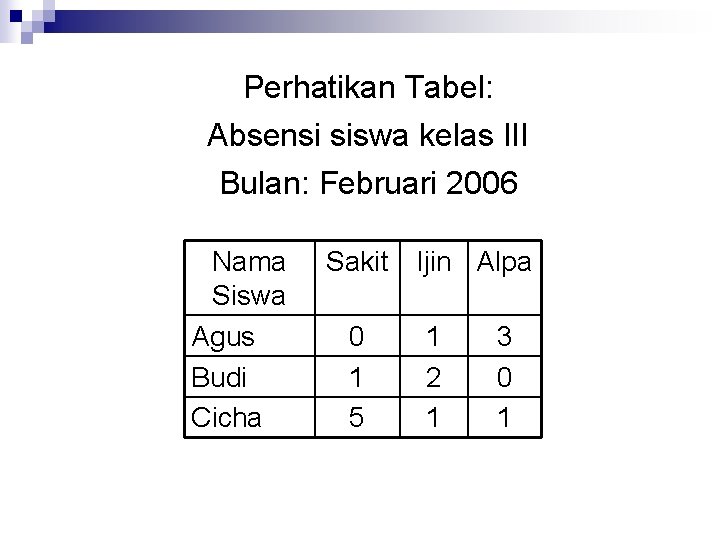
Perhatikan Tabel: Absensi siswa kelas III Bulan: Februari 2006 Nama Siswa Agus Budi Cicha Sakit Ijin Alpa 0 1 5 1 2 1 3 0 1

Jika judul baris dan kolom dihilangkan Nama Siswa Sakit Agus 0 Budi 1 Cicha 5 Judul baris Ijin Alpa 1 2 1 3 0 1 Judul kolom

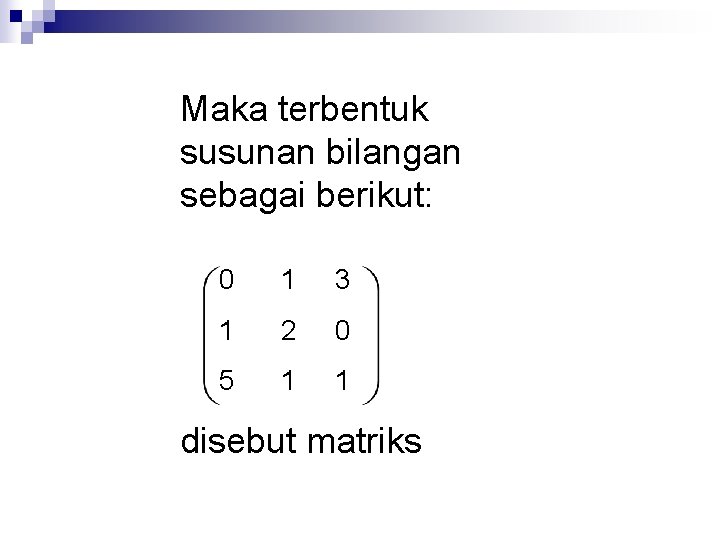
Maka terbentuk susunan bilangan sebagai berikut: 0 1 3 1 2 0 5 1 1 disebut matriks

DEFINISI MATRIKS Matriks adalah Susunan bilangan berbentuk persegipanjang yang diatur dalam baris dan kolom, ditulis diantara kurung kecil atau siku

Bilangan yang disusun disebut elemen. Banyak baris x banyak kolom disebut ordo matriks. Sebuah matriks ditulis dengan huruf besar

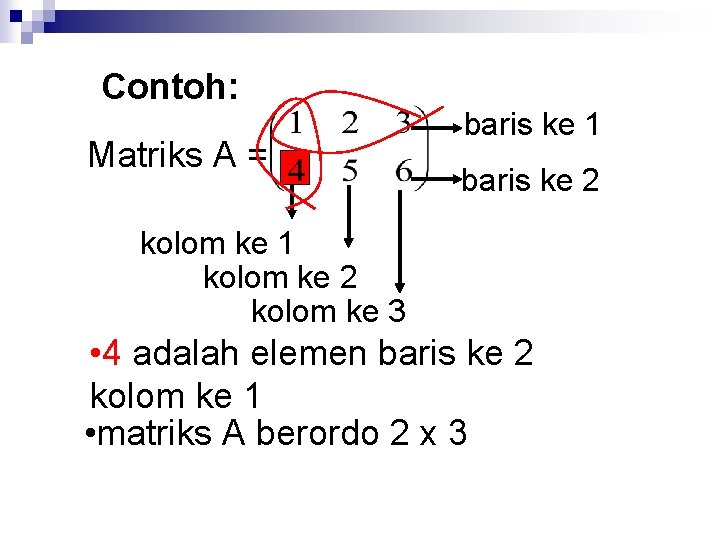
Contoh: Matriks A = baris ke 1 baris ke 2 kolom ke 1 kolom ke 2 kolom ke 3 • 4 adalah elemen baris ke 2 kolom ke 1 • matriks A berordo 2 x 3

Matriks persegi Adalah matriks yang banyak baris dan kolom sama

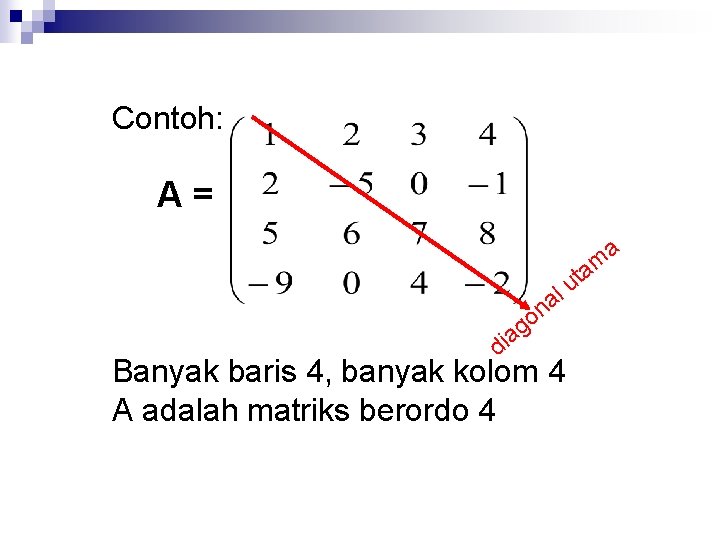
Contoh: A= a am t u l a n o g a di Banyak baris 4, banyak kolom 4 A adalah matriks berordo 4

Perhatikan matriks berikut: A= A adalah matriks segitiga atas yaitu matriks yang elemen-elemen di bawah diagonal utamanya bernilai nol

Perhatikan matriks berikut: B= B adalah matriks segitiga bawah yaitu matriks yang elemen-elemen di atas diagonal utamanya bernilai nol

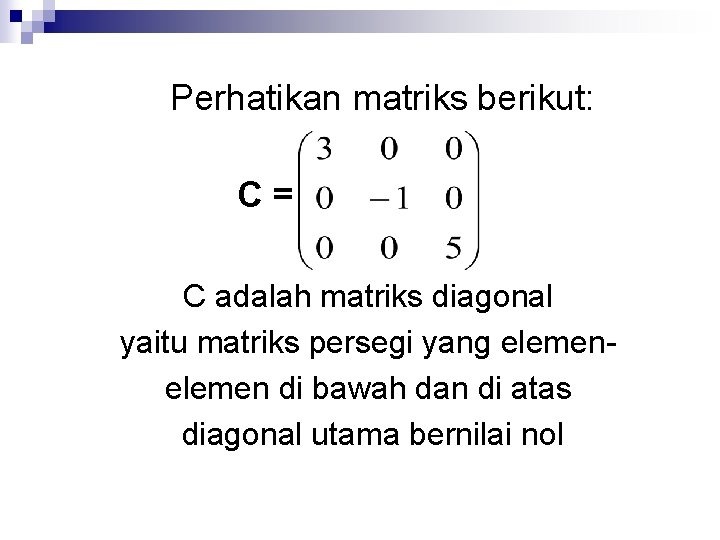
Perhatikan matriks berikut: C= C adalah matriks diagonal yaitu matriks persegi yang elemen di bawah dan di atas diagonal utama bernilai nol

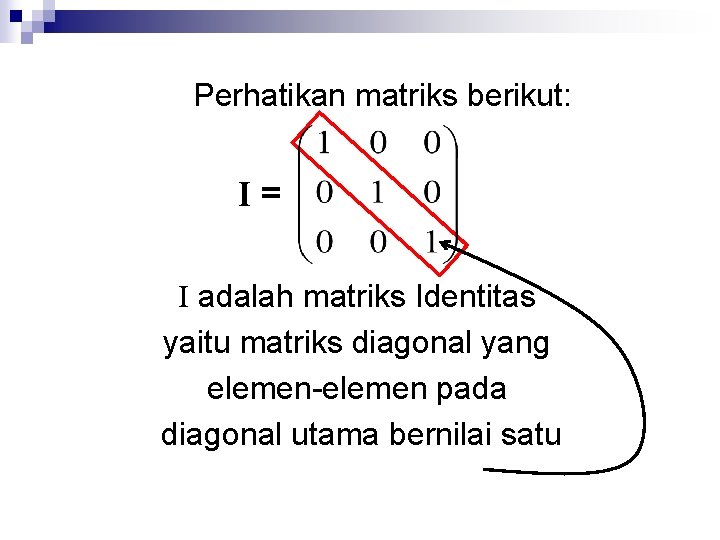
Perhatikan matriks berikut: I= I adalah matriks Identitas yaitu matriks diagonal yang elemen-elemen pada diagonal utama bernilai satu

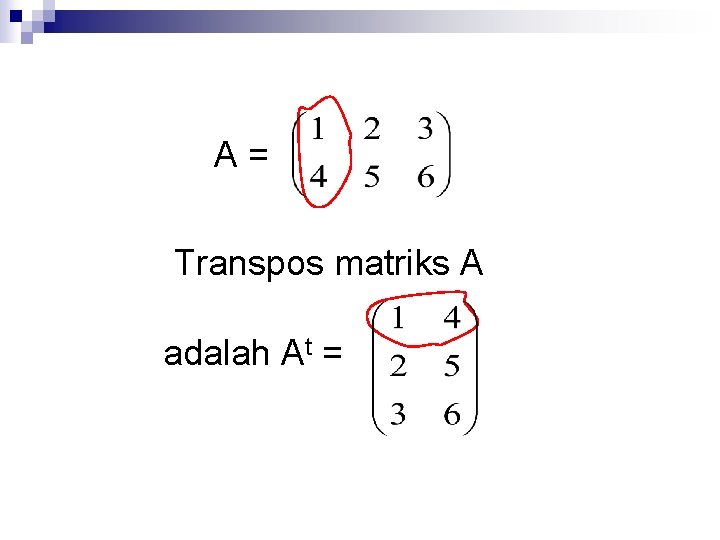
Transpos Matriks Transpos matriks A, ditulis At adalah matriks baru dimana elemen baris matriks At merupakan kolom matriks A

A= Transpos matriks A adalah At =

Kesamaan Dua Matriks matriks A = matriks B jika Ø ordo matriks A = ordo matriks B Øelemen yang seletak sama

A= dan B = Jika matriks A = matriks B, maka x – 7 = 6 x = 13 2 y = -1 y = -½

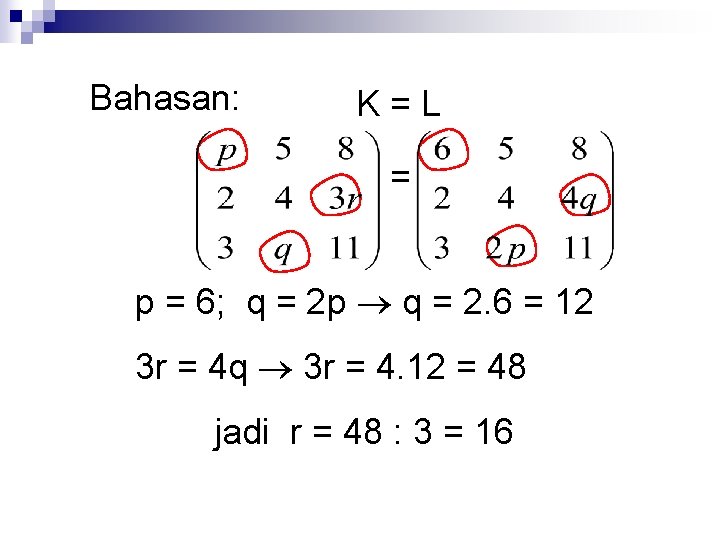
Contoh 1: Diketahui K = dan L = Jika K = L, maka r adalah….

Bahasan: K=L = p = 6; q = 2 p q = 2. 6 = 12 3 r = 4 q 3 r = 4. 12 = 48 jadi r = 48 : 3 = 16

Contoh 2: Misalkan A = dan B = Jika At adalah transpos matriks A maka persamaan At = B dipenuhi bila x = ….

Bahasan: A= At = B =

x+y=1 x–y=3 2 x = 4 Jadi x = 4 : 2 = 2

Operasi Pada Matriks ØPenjumlahan ØPengurangan ØPerkalian: perkalian skalar dengan matriks perkalian matriks dengan matriks

Penjumlahan/pengurangan Matriks A dan B dapat dijumlahkan/dikurangkan, jika ordonya sama. Hasilnya merupakan jumlah/selisih elemen-elemen yang seletak

Contoh 1: A= dan B = A + B = + =

Contoh 2: Jika A = , B= dan C = Maka (A + C) – (A + B) =….

Perkalian skalar dengan matriks Jika k suatu bilangan (skalar) maka perkalian k dengan matriks A ditulis k. A, adalah matriks yang elemennya diperoleh dari hasil kali k dengan setiap elemen matriks A

Contoh 1: Matriks A = Tentukan elemen-elemen matriks 5 A! Jawab: 5 A =

Contoh 2: Matriks A = , B= dan C = Jika A – 2 B = 3 C, maka a + b = ….

Bahasan A – 2 B = 3 C – 2 = 3 – =

Contoh 3: Matriks A = dan B = Supaya dipenuhi A = 2 Bt, dengan Bt adalah matriks transpos dari B maka nilai m = ….

Bahasan B= berarti Bt = A = 2 Bt =

= 4 = 2 k k = 2 2 l = 4 k + 2 2 l = 4. 2 + 2 2 l = 10 l = 5 3 m = 2 l + 14 3 m = 2. 5 + 14 = 24 Jadi m = 8