MENG 372 Chapter 9 Gears All figures taken

MENG 372 Chapter 9 Gears All figures taken from Design of Machinery, 3 rd ed. Robert Norton 2003

Rolling Cylinders • Gear analysis is based on rolling cylinders • External gears rotate in opposite directions • Internal gears rotate in same direction

Gear Types • Internal and external gears • Two gears together are called a gearset

Fundamental Law of Gearing • The angular velocity ratio between 2 meshing gears remains constant throughout the mesh • Angular velocity ratio (m. V) • Torque ratio (m. T) is mechanical advantage (m. A) Input Output

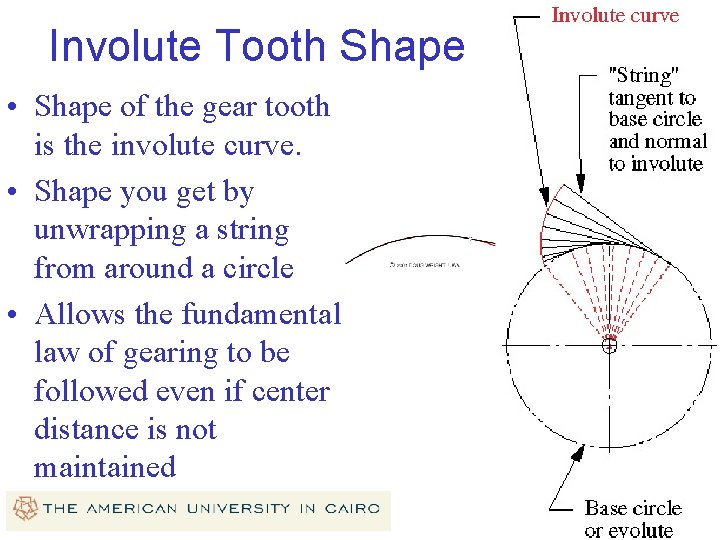
Involute Tooth Shape • Shape of the gear tooth is the involute curve. • Shape you get by unwrapping a string from around a circle • Allows the fundamental law of gearing to be followed even if center distance is not maintained

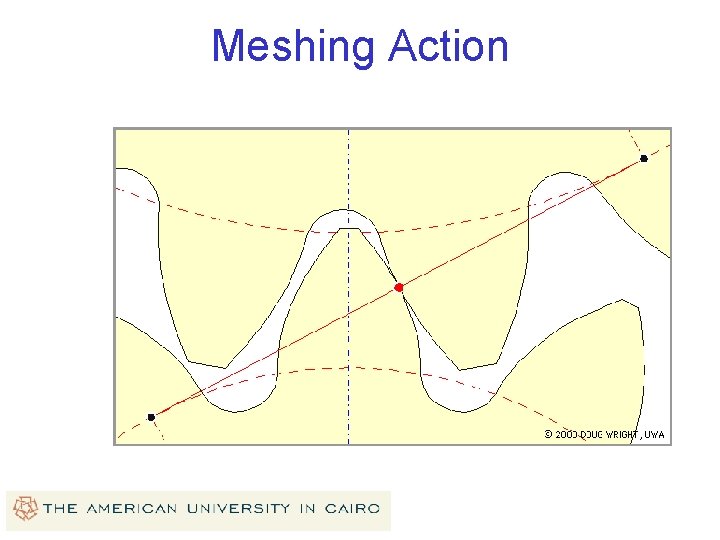
Meshing Action

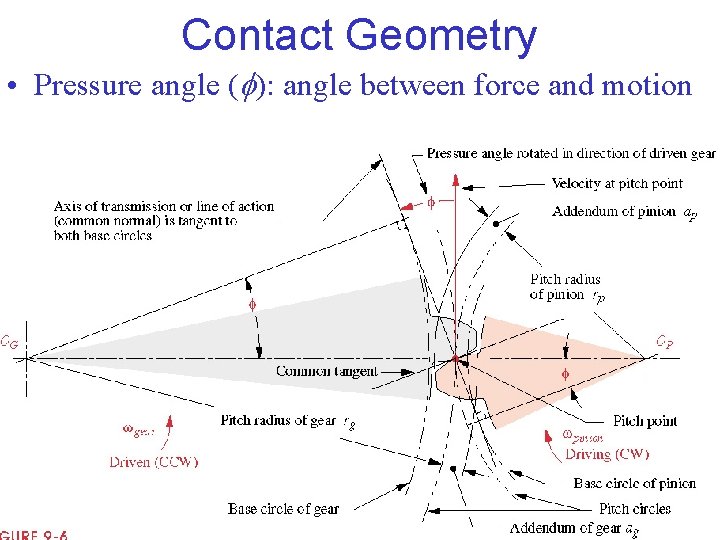
Contact Geometry • Pressure angle (f): angle between force and motion

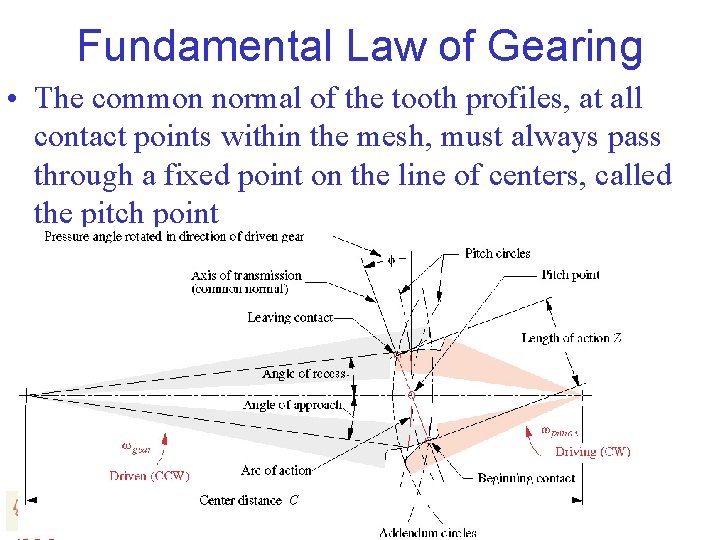
Fundamental Law of Gearing • The common normal of the tooth profiles, at all contact points within the mesh, must always pass through a fixed point on the line of centers, called the pitch point

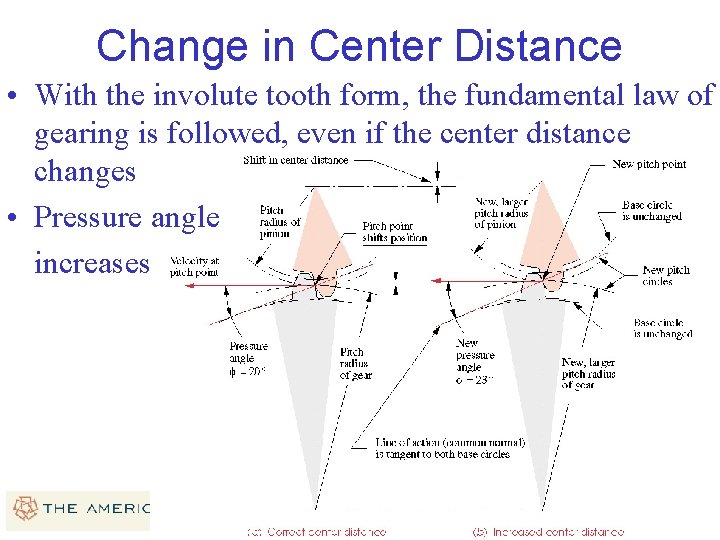
Change in Center Distance • With the involute tooth form, the fundamental law of gearing is followed, even if the center distance changes • Pressure angle increases

Backlash • Backlash – the clearance between mating teeth measured at the pitch circle • Whenever torque changes sign, teeth will move from one side of contact to another • Can cause an error in position • Backlash increases with increase in center distance • Can have anti-backlash gears (two gears, back to back)

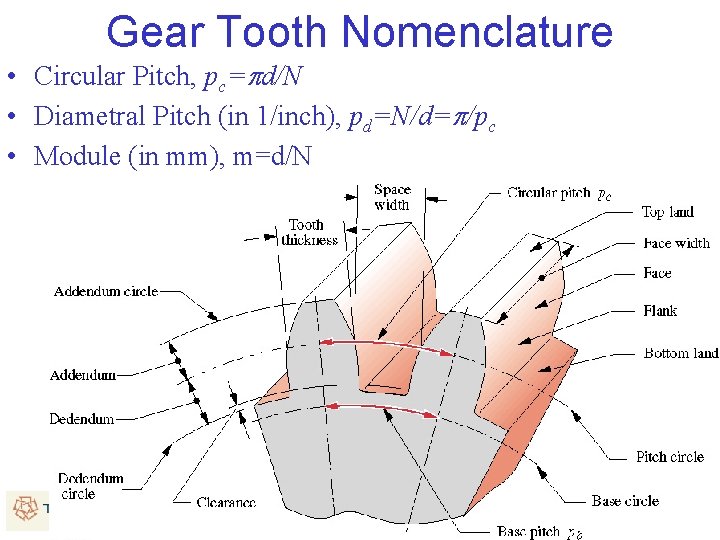
Gear Tooth Nomenclature • Circular Pitch, pc=pd/N • Diametral Pitch (in 1/inch), pd=N/d=p/pc • Module (in mm), m=d/N

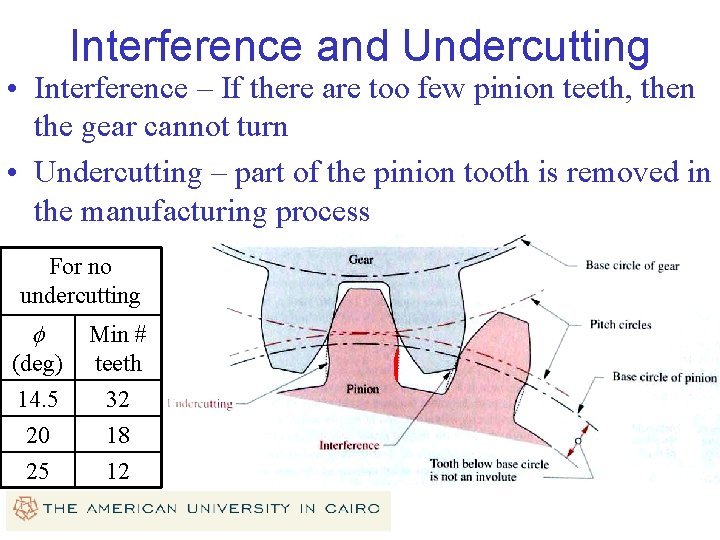
Interference and Undercutting • Interference – If there are too few pinion teeth, then the gear cannot turn • Undercutting – part of the pinion tooth is removed in the manufacturing process For no undercutting f (deg) Min # teeth 14. 5 20 25 32 18 12

Gear Types • • • Spur Gears Helical Gears (open or crossed) Herringbone Gears Worm Gears Rack and Pinion Bevel Gears

Spur Gears • Straight teeth • Noisy since all of the tooth contacts at one time • Low Cost • High efficiency (9899%)

Helical Gears • • Slanted teeth to smooth contact Axis can be parallel or crossed Has a thrust force Efficiency of 96 -98% for parallel and 50 -90% for crossed

Crossed Helical Gears

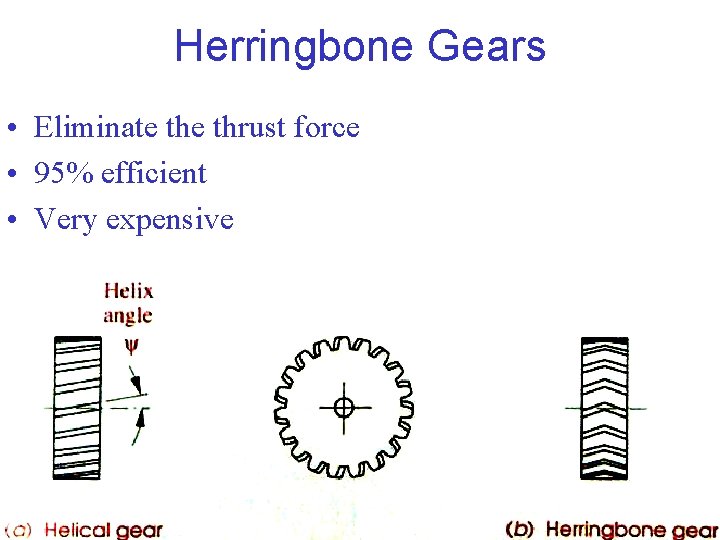
Herringbone Gears • Eliminate thrust force • 95% efficient • Very expensive

Rack and Pinion • Generates linear motion • Teeth are straight (one way to cut a involute form)

Worm Gears • • Worm gear has one or two teeth High gear ratio Impossible to back drive 40 -85% efficient

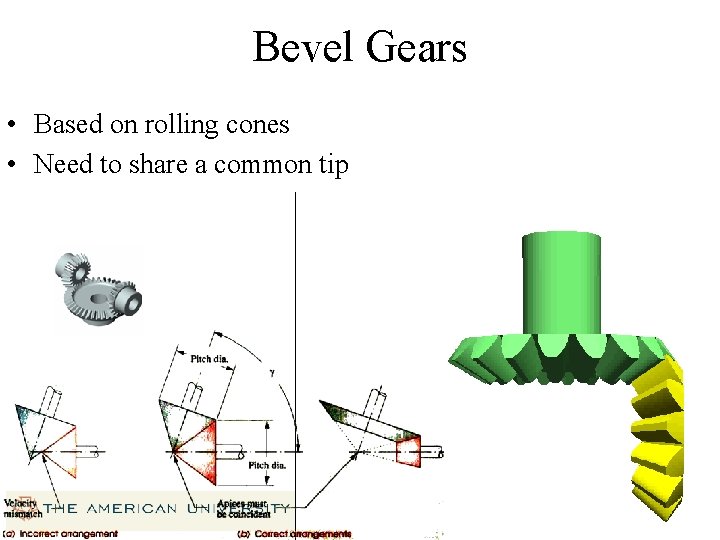
Bevel Gears • Based on rolling cones • Need to share a common tip

Other Gear Types • Noncircular gears – give a different velocity ratio at different angles • Synchronous belts and sprockets – like pulleys (98% efficient)

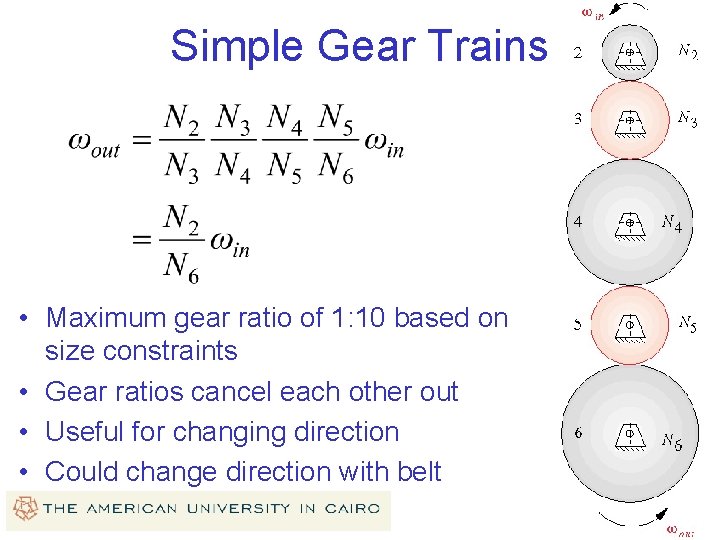
Simple Gear Trains • Maximum gear ratio of 1: 10 based on size constraints • Gear ratios cancel each other out • Useful for changing direction • Could change direction with belt

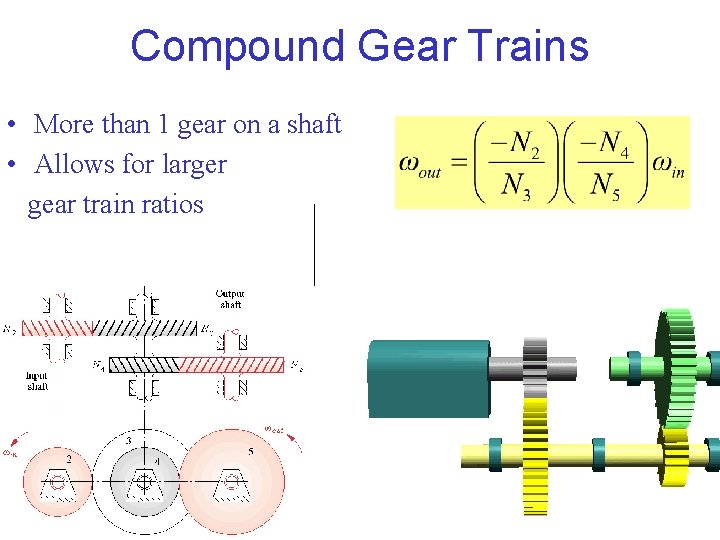
Compound Gear Trains • More than 1 gear on a shaft • Allows for larger gear train ratios

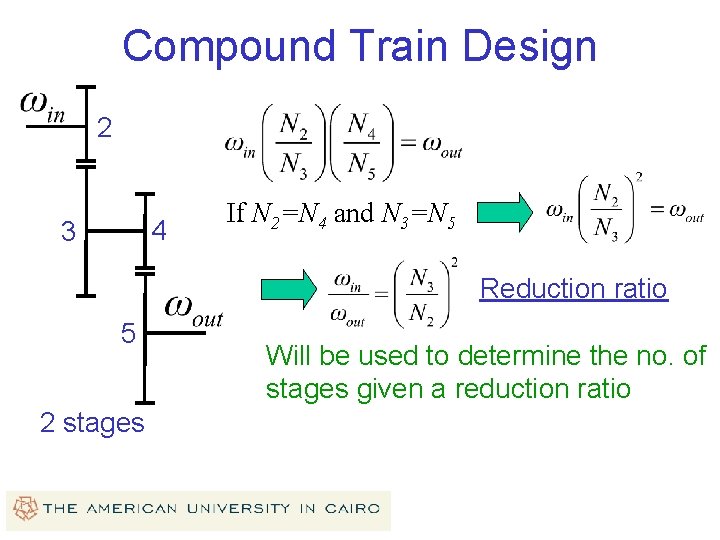
Compound Train Design 2 4 3 If N 2=N 4 and N 3=N 5 Reduction ratio 5 2 stages Will be used to determine the no. of stages given a reduction ratio

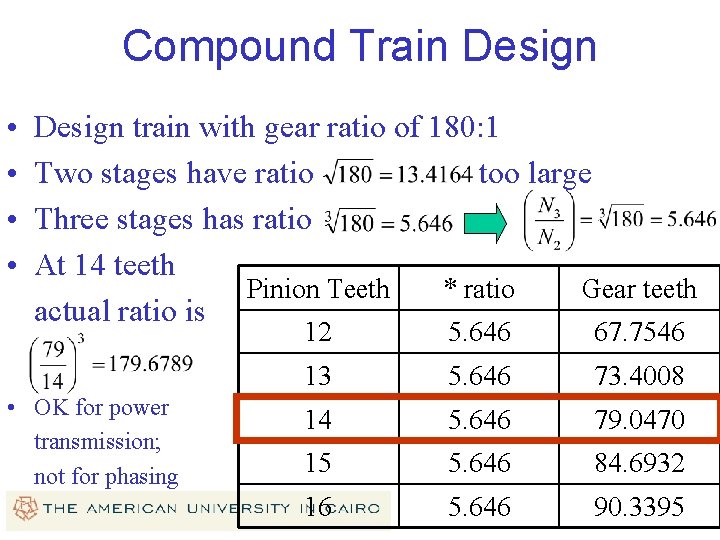
Compound Train Design • • Design train with gear ratio of 180: 1 Two stages have ratio too large Three stages has ratio At 14 teeth Pinion Teeth * ratio Gear teeth actual ratio is • OK for power transmission; not for phasing 12 5. 646 67. 7546 13 5. 646 73. 4008 14 5. 646 79. 0470 15 5. 646 84. 6932 16 5. 646 90. 3395

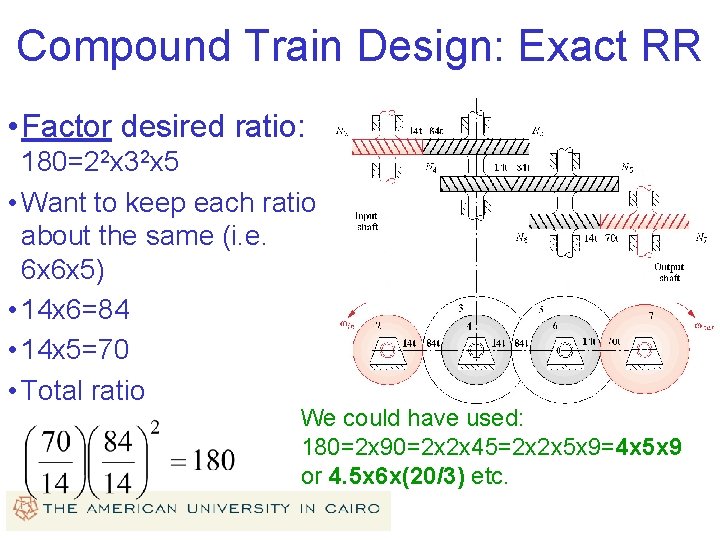
Compound Train Design: Exact RR • Factor desired ratio: 180=22 x 32 x 5 • Want to keep each ratio about the same (i. e. 6 x 6 x 5) • 14 x 6=84 • 14 x 5=70 • Total ratio We could have used: 180=2 x 90=2 x 2 x 45=2 x 2 x 5 x 9=4 x 5 x 9 or 4. 5 x 6 x(20/3) etc.

Manual Transmission

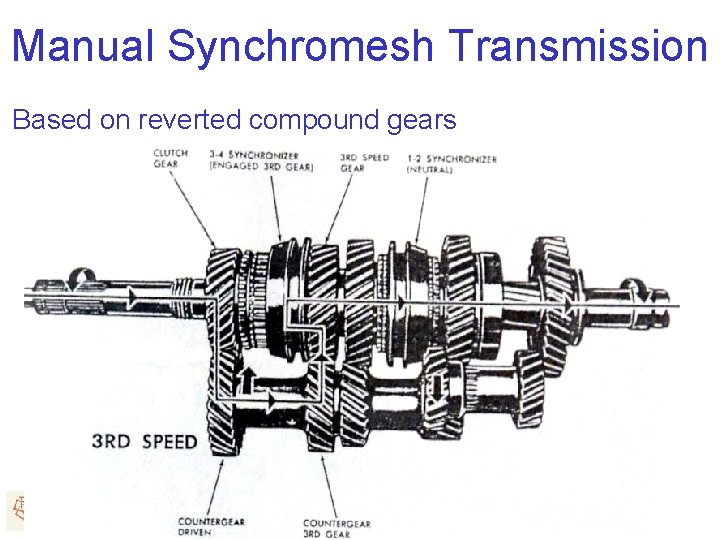
Manual Synchromesh Transmission Based on reverted compound gears

Reverted Compound Train • Input and output shafts are aligned • For reverted gear trains: R 2+R 3=R 4+R 5 D 2+D 3=D 4+D 5 N 2+N 3=N 4+N 5 • Gear ratio is Commercial three stage reverted compound train

Design a reverted compound gear train for a gear ratio of 18: 1 18=3 x 6 N 3=6 N 2, N 5=3 N 4 N 2+N 3=N 4+N 5=constant N 2+6 N 2=N 4+3 N 4=C 7 N 2=4 N 4=C Ø Take C=28, then N 2=4, N 4=7 Ø This is too small for a gear! Choose C=28 x 4=112 (say) • N 2=16, N 3=96, • N 4=28, N 5=84

Planetary or Epicyclic Gears • Conventional gearset has one DOF • If you remove the ground at gear 3, it has two DOF • It is difficult to access w 3

Planetary Gearset with Fixed Ring Planetary Gearset with Fixed Arm

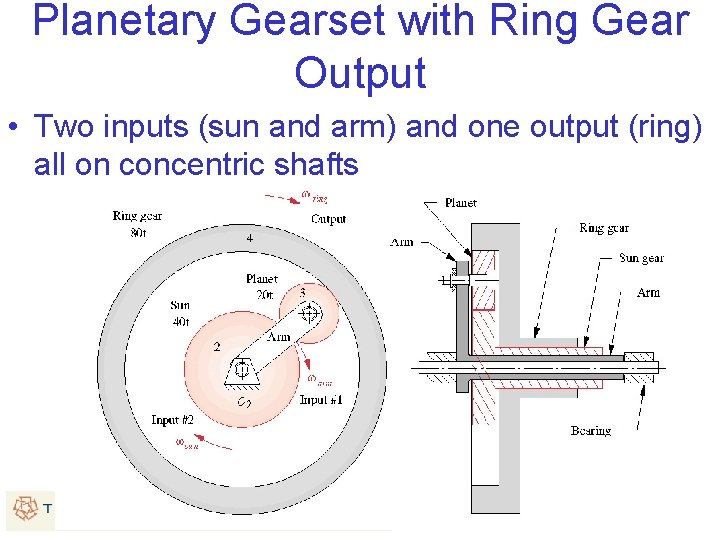
Planetary Gearset with Ring Gear Output • Two inputs (sun and arm) and one output (ring) all on concentric shafts

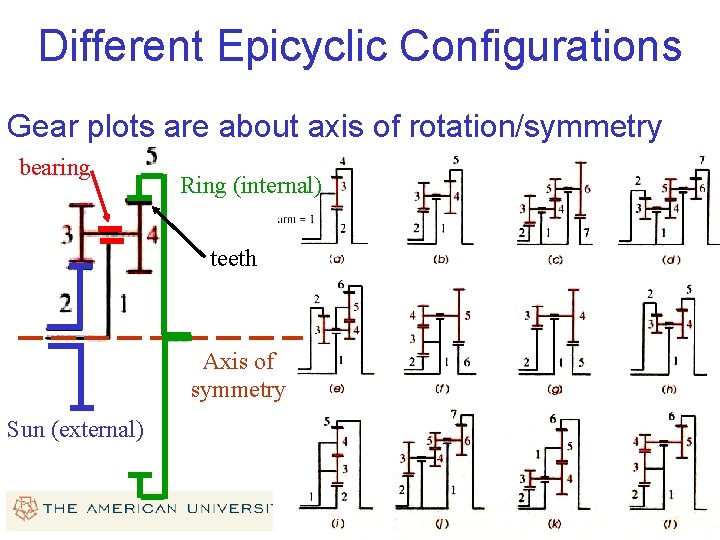
Different Epicyclic Configurations Gear plots are about axis of rotation/symmetry bearing Ring (internal) teeth Axis of symmetry Sun (external)

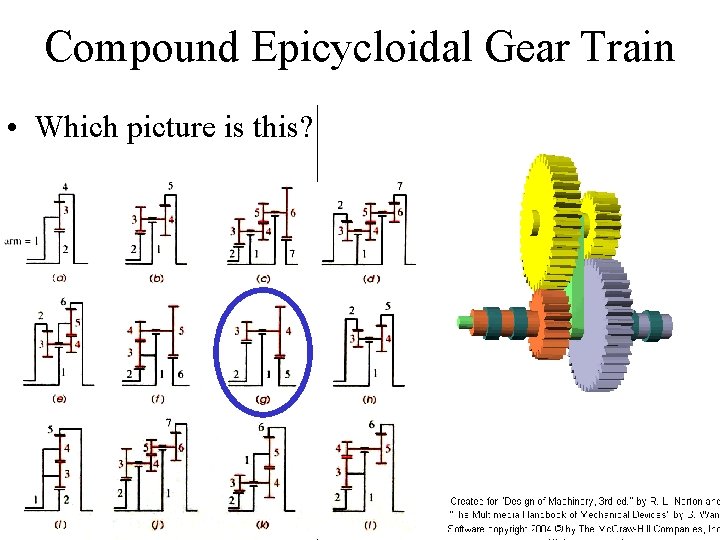
Compound Epicycloidal Gear Train • Which picture is this?

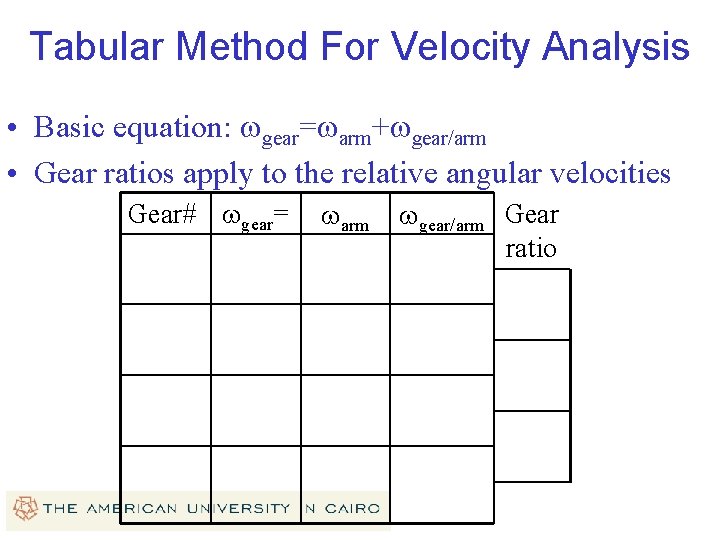
Tabular Method For Velocity Analysis • Basic equation: wgear=warm+wgear/arm • Gear ratios apply to the relative angular velocities Gear# wgear= warm wgear/arm Gear ratio

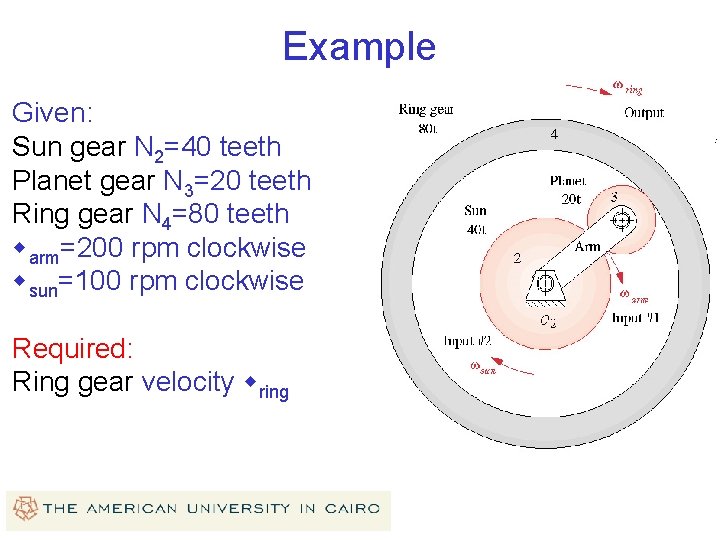
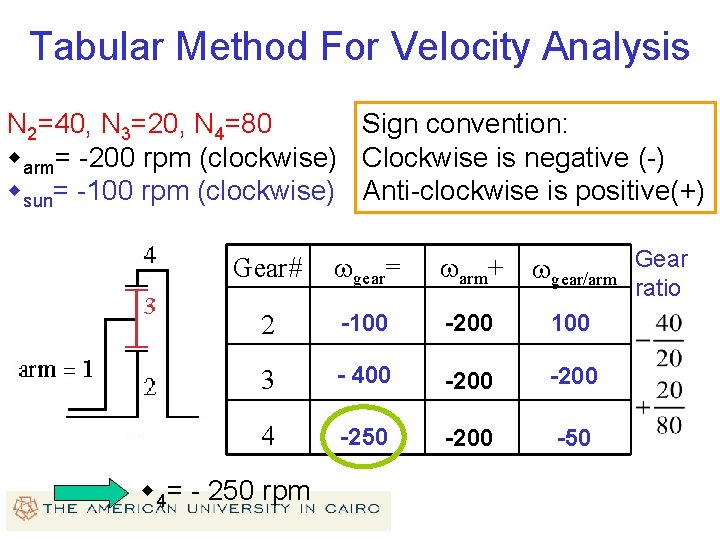
Example Given: Sun gear N 2=40 teeth Planet gear N 3=20 teeth Ring gear N 4=80 teeth warm=200 rpm clockwise wsun=100 rpm clockwise Required: Ring gear velocity wring

Tabular Method For Velocity Analysis Sign convention: N 2=40, N 3=20, N 4=80 warm= -200 rpm (clockwise) Clockwise is negative (-) wsun= -100 rpm (clockwise) Anti-clockwise is positive(+) wgear/arm Gear# wgear= warm+ 2 -100 -200 100 3 - 400 -200 4 -250 -200 -50 w 4= - 250 rpm ratio

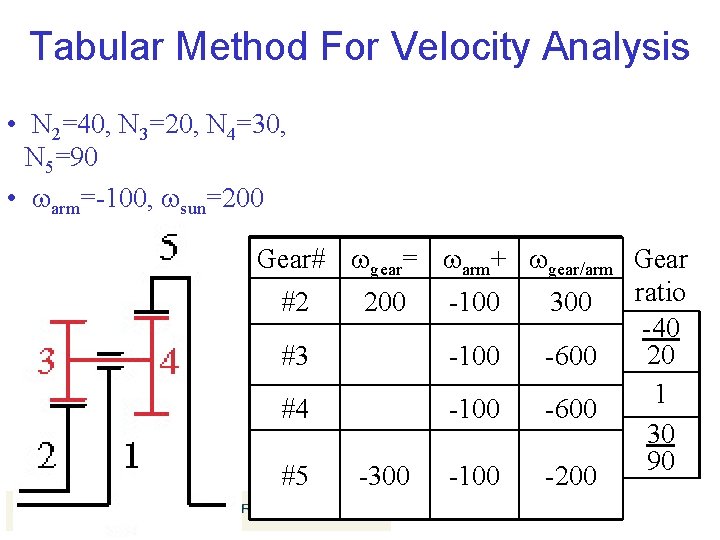
Tabular Method For Velocity Analysis • N 2=40, N 3=20, N 4=30, N 5=90 • warm=-100, wsun=200 Gear# wgear= wwarm arm+ wgear/arm Gear ratio #2 200 -100 300 -40 20 #3 -100 -600 1 #4 -100 -600 30 90 #5 -300 -100 -200

Equation Method For Velocity Analysis • N 2=40, N 3=20, N 4=30, N 5=90 • warm=-100 rpm, wsun=200