Memory Hierarchy Motivation Definitions Four Questions about Memory

Memory Hierarchy— Motivation, Definitions, Four Questions about Memory Hierarchy, Improving Performance Professor Alvin R. Lebeck Computer Science 220 ECE 252 Fall 2008

Admin • Some stuff will be review…some will not • Projects… • Reading – H&P Appendix C & Chapter 5 • There will be three papers to read © Alvin R. Lebeck 2008 2

Outline of Today’s Lecture • • • Most of today should be review…later stuff will not The Memory Hierarchy Direct Mapped Cache. Two-Way Set Associative Cache Fully Associative cache Replacement Policies Write Strategies Memory Hierarchy Performance Improving Performance © Alvin R. Lebeck 2008 3

Cache • • What is a cache? What is the motivation for a cache? Why do caches work? How do caches work? © Alvin R. Lebeck 2008 4

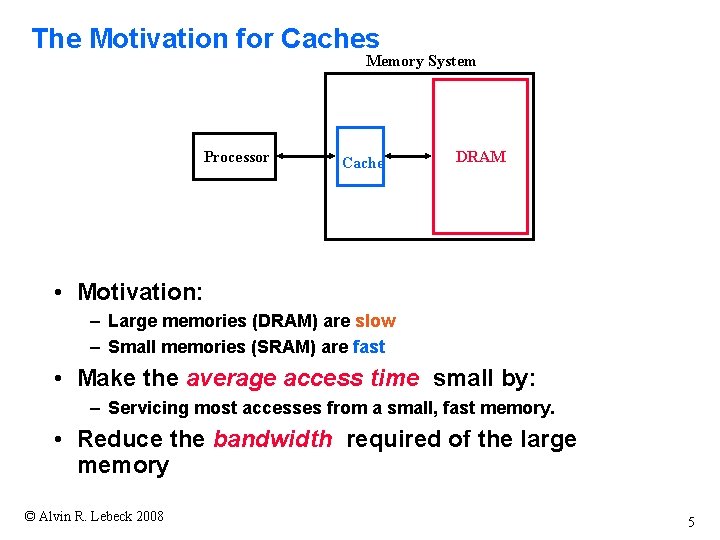
The Motivation for Caches Memory System Processor Cache DRAM • Motivation: – Large memories (DRAM) are slow – Small memories (SRAM) are fast • Make the average access time small by: – Servicing most accesses from a small, fast memory. • Reduce the bandwidth required of the large memory © Alvin R. Lebeck 2008 5

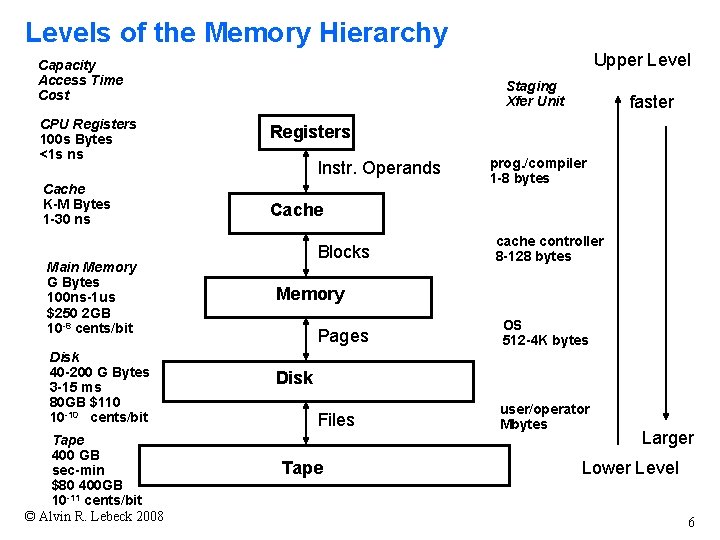
Levels of the Memory Hierarchy Upper Level Capacity Access Time Cost Staging Xfer Unit CPU Registers 100 s Bytes <1 s ns Registers Cache K-M Bytes 1 -30 ns Cache Main Memory G Bytes 100 ns-1 us $250 2 GB 10 -8 cents/bit Disk 40 -200 G Bytes 3 -15 ms 80 GB $110 10 -10 cents/bit Tape 400 GB sec-min $80 400 GB 10 -11 cents/bit © Alvin R. Lebeck 2008 Instr. Operands Blocks faster prog. /compiler 1 -8 bytes cache controller 8 -128 bytes Memory Pages OS 512 -4 K bytes Files user/operator Mbytes Disk Tape Larger Lower Level 6

The Principle of Locality Probability of reference 0 Address Space 2 n • The Principle of Locality: – Program access a relatively small portion of the address space at any instant of time. – Example: 90% of time in 10% of the code • Two Different Types of Locality: – Temporal Locality (Locality in Time): If an item is referenced, it will tend to be referenced again soon. – Spatial Locality (Locality in Space): If an item is referenced, items whose addresses are close by tend to be referenced soon. © Alvin R. Lebeck 2008 7

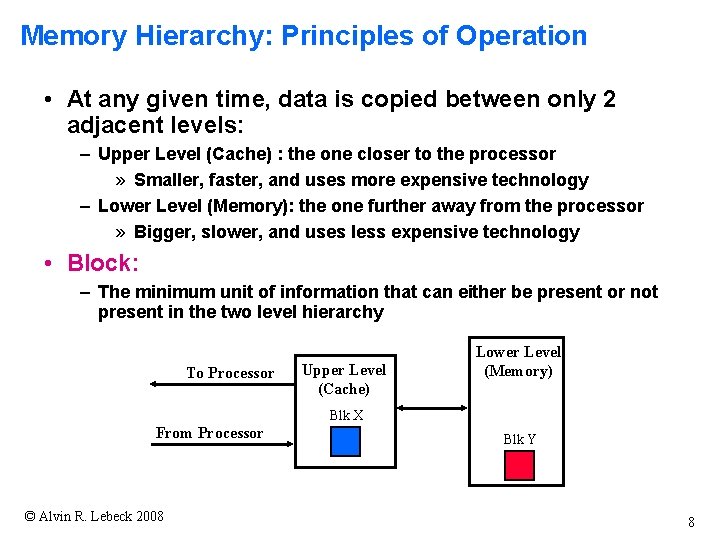
Memory Hierarchy: Principles of Operation • At any given time, data is copied between only 2 adjacent levels: – Upper Level (Cache) : the one closer to the processor » Smaller, faster, and uses more expensive technology – Lower Level (Memory): the one further away from the processor » Bigger, slower, and uses less expensive technology • Block: – The minimum unit of information that can either be present or not present in the two level hierarchy To Processor Upper Level (Cache) Lower Level (Memory) Blk X From Processor © Alvin R. Lebeck 2008 Blk Y 8

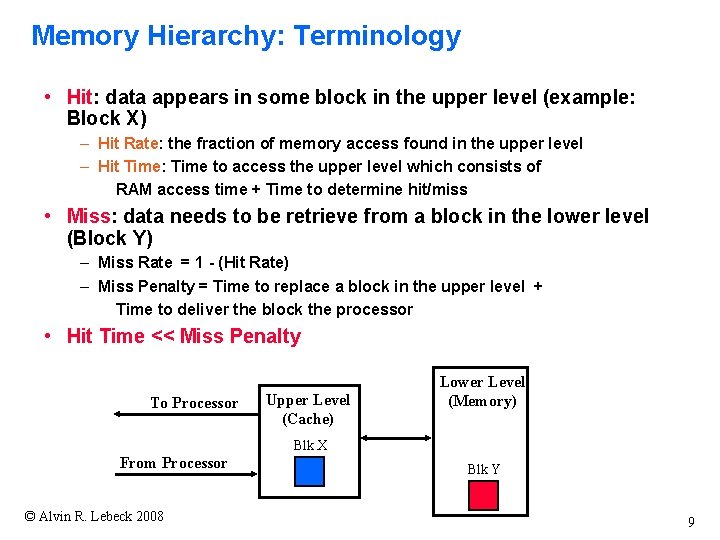
Memory Hierarchy: Terminology • Hit: data appears in some block in the upper level (example: Block X) – Hit Rate: the fraction of memory access found in the upper level – Hit Time: Time to access the upper level which consists of RAM access time + Time to determine hit/miss • Miss: data needs to be retrieve from a block in the lower level (Block Y) – Miss Rate = 1 - (Hit Rate) – Miss Penalty = Time to replace a block in the upper level + Time to deliver the block the processor • Hit Time << Miss Penalty To Processor Upper Level (Cache) Lower Level (Memory) Blk X From Processor © Alvin R. Lebeck 2008 Blk Y 9

Four Questions for Memory Hierarchy Designers • Q 1: Where can a block be placed in the upper level? (Block placement) • Q 2: How is a block found if it is in the upper level? (Block identification) • Q 3: Which block should be replaced on a miss? (Block replacement) • Q 4: What happens on a write? (Write strategy) © Alvin R. Lebeck 2008 10

Direct Mapped Cache l Direct Mapped cache is an array of fixed size frames. Each frame holds consecutive bytes (cache block) of main memory data. l l The Tag Array holds the Block Memory Address. A valid bit associated with each cache block tells if the data is valid. l Cache Index: The location of a block (and it’s tag) in the cache. l l Block Offset: The byte location in the cache block. Cache-Index = (<Address> Mod (Cache_Size))/ Block_Size Block-Offset = <Address> Mod (Block_Size) Tag = <Address> / (Cache_Size) © Alvin R. Lebeck 2008 11

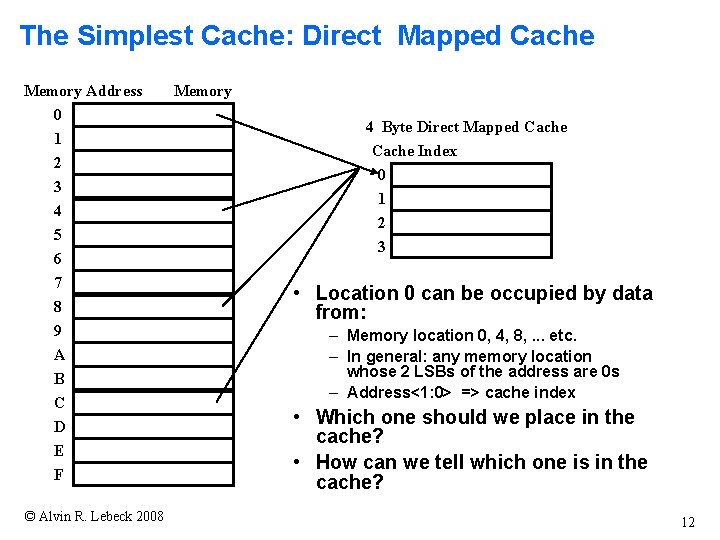
The Simplest Cache: Direct Mapped Cache Memory Address 0 1 2 3 4 5 6 7 8 9 A B C D E F © Alvin R. Lebeck 2008 Memory 4 Byte Direct Mapped Cache Index 0 1 2 3 • Location 0 can be occupied by data from: – Memory location 0, 4, 8, . . . etc. – In general: any memory location whose 2 LSBs of the address are 0 s – Address<1: 0> => cache index • Which one should we place in the cache? • How can we tell which one is in the cache? 12

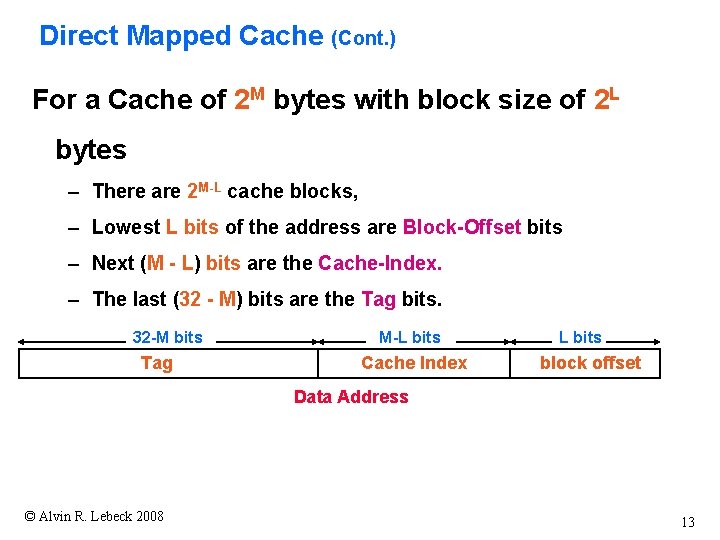
Direct Mapped Cache (Cont. ) For a Cache of 2 M bytes with block size of 2 L bytes – There are 2 M-L cache blocks, – Lowest L bits of the address are Block-Offset bits – Next (M - L) bits are the Cache-Index. – The last (32 - M) bits are the Tag bits. 32 -M bits Tag M-L bits Cache Index L bits block offset Data Address © Alvin R. Lebeck 2008 13

Example: 1 -KB Cache with 32 B blocks: Cache Index = (<Address> Mod (1024))/ 32 Block-Offset = <Address> Mod (32) Tag = <Address> / (1024) 22 bits Tag 5 bits Cache Index 5 bits block offset Address Valid bit Cache Tag 22 bits Direct Mapped Cache Data 32 -byte block Byte 31 Byte 30 © Alvin R. Lebeck 2008 1 K = 210 = 1024 25 = 32 . . Byte 1 Byte 0 32 cache blocks 14

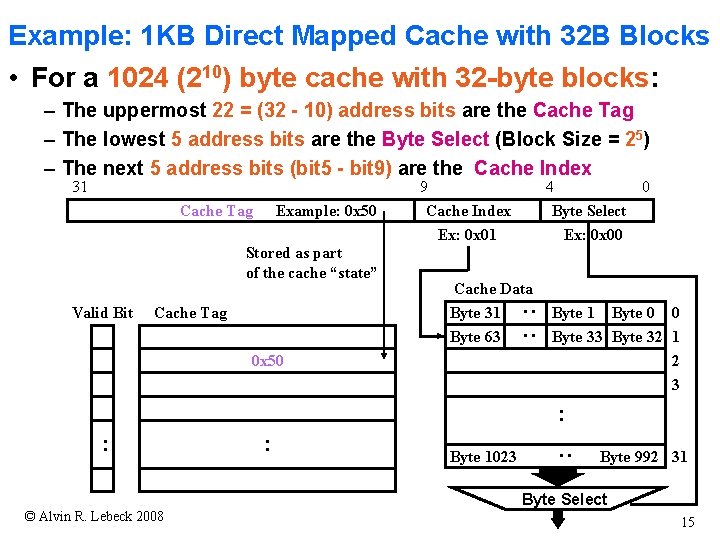
Example: 1 KB Direct Mapped Cache with 32 B Blocks • For a 1024 (210) byte cache with 32 -byte blocks: – The uppermost 22 = (32 - 10) address bits are the Cache Tag – The lowest 5 address bits are the Byte Select (Block Size = 25) – The next 5 address bits (bit 5 - bit 9) are the Cache Index 31 Cache Tag Example: 0 x 50 Stored as part of the cache “state” Cache Tag 4 0 Byte Select Ex: 0 x 00 Cache Data Byte 31 Byte 63 : : Valid Bit 9 Cache Index Ex: 0 x 01 0 x 50 Byte 1 Byte 0 0 Byte 33 Byte 32 1 2 3 : : Byte 1023 : : Byte 992 31 Byte Select © Alvin R. Lebeck 2008 15

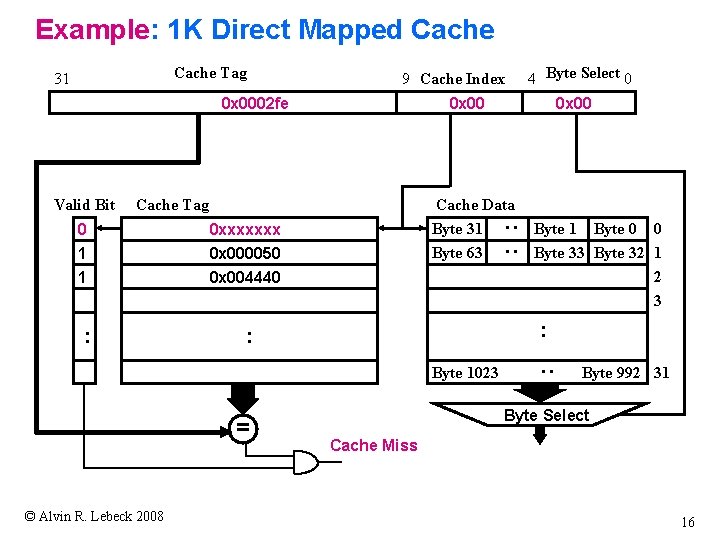
Example: 1 K Direct Mapped Cache 9 Cache Index 0 x 0002 fe 0 x 00 Cache Tag 0 0 xxxxxxx 1 1 0 x 000050 0 x 004440 : 0 x 00 Cache Data Byte 31 Byte 63 : : Valid Bit Byte 1023 © Alvin R. Lebeck 2008 Byte 1 Byte 0 0 Byte 33 Byte 32 1 2 3 : : = 4 Byte Select 0 : Cache Tag 31 Byte 992 31 Byte Select Cache Miss 16

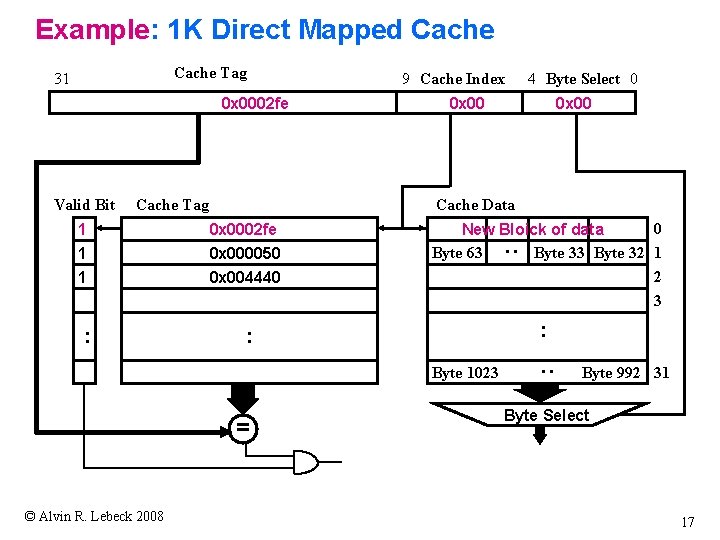
Example: 1 K Direct Mapped Cache Tag 31 0 x 0002 fe Valid Bit Cache Tag 9 Cache Index 4 Byte Select 0 0 x 00 Cache Data 0 x 0002 fe 1 1 0 x 000050 0 x 004440 0 New Bloick of data Byte 63 Byte 32 1 2 3 : : Byte 1023 = © Alvin R. Lebeck 2008 : : : 1 Byte 992 31 Byte Select 17

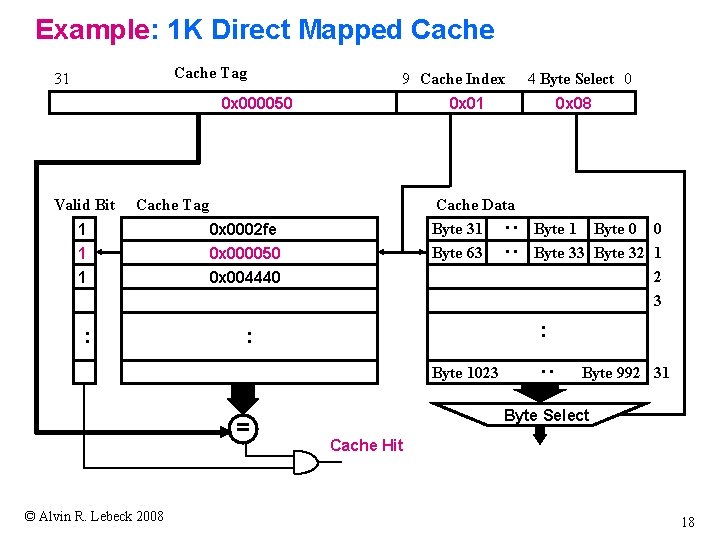
Example: 1 K Direct Mapped Cache 9 Cache Index 0 x 000050 0 x 01 Cache Tag 1 0 x 0002 fe 1 1 0 x 000050 0 x 004440 : 0 x 08 Cache Data Byte 31 Byte 63 : : Valid Bit Byte 1023 © Alvin R. Lebeck 2008 Byte 1 Byte 0 0 Byte 33 Byte 32 1 2 3 : : = 4 Byte Select 0 : Cache Tag 31 Byte 992 31 Byte Select Cache Hit 18

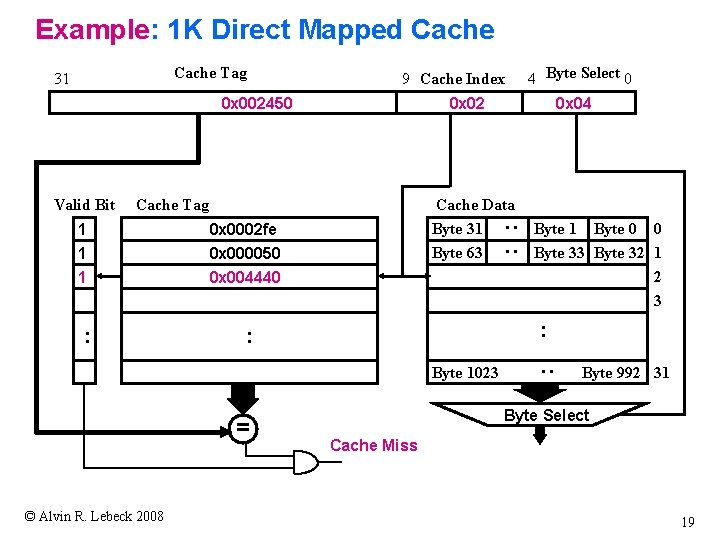
Example: 1 K Direct Mapped Cache 9 Cache Index 0 x 002450 0 x 02 Cache Tag 1 0 x 0002 fe 1 1 0 x 000050 0 x 004440 : 0 x 04 Cache Data Byte 31 Byte 63 : : Valid Bit Byte 1023 © Alvin R. Lebeck 2008 Byte 1 Byte 0 0 Byte 33 Byte 32 1 2 3 : : = 4 Byte Select 0 : Cache Tag 31 Byte 992 31 Byte Select Cache Miss 19

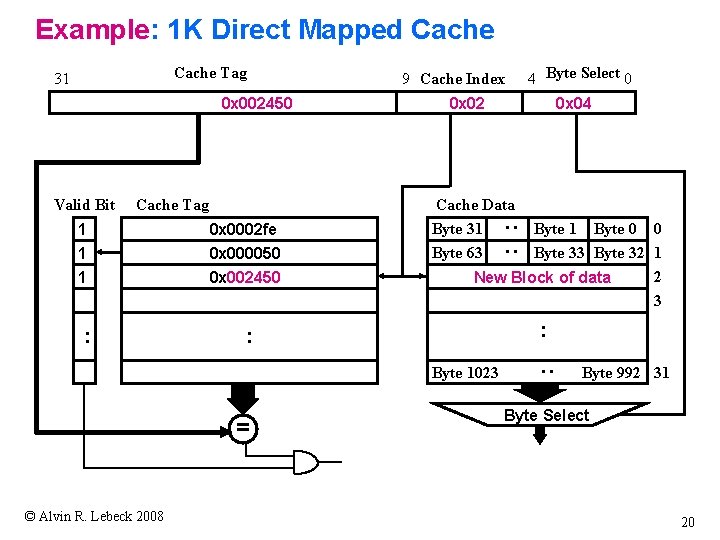
Example: 1 K Direct Mapped Cache Valid Bit Cache Tag 1 0 x 0002 fe 1 1 0 x 000050 0 x 002450 : 0 x 02 0 x 04 Cache Data Byte 31 Byte 63 Byte 1 Byte 0 0 Byte 33 Byte 32 1 2 New Block of data 3 : : Byte 1023 = © Alvin R. Lebeck 2008 4 Byte Select 0 : 0 x 002450 9 Cache Index : : Cache Tag 31 Byte 992 31 Byte Select 20

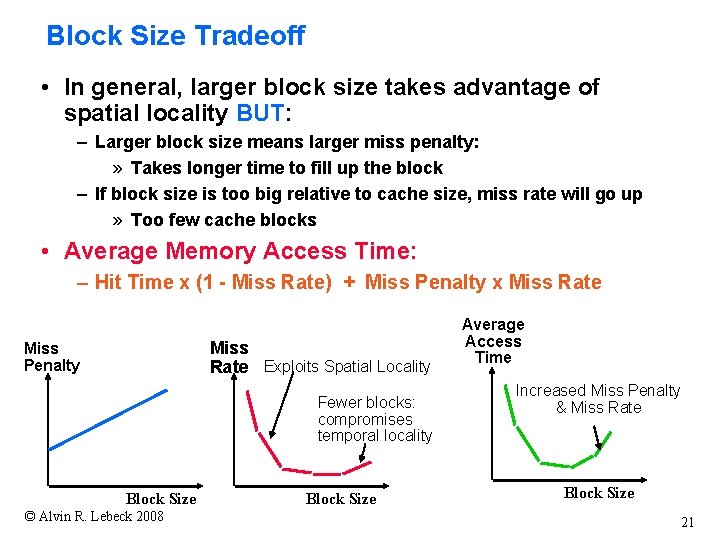
Block Size Tradeoff • In general, larger block size takes advantage of spatial locality BUT: – Larger block size means larger miss penalty: » Takes longer time to fill up the block – If block size is too big relative to cache size, miss rate will go up » Too few cache blocks • Average Memory Access Time: – Hit Time x (1 - Miss Rate) + Miss Penalty x Miss Rate Exploits Spatial Locality Miss Penalty Fewer blocks: compromises temporal locality Block Size © Alvin R. Lebeck 2008 Block Size Average Access Time Increased Miss Penalty & Miss Rate Block Size 21

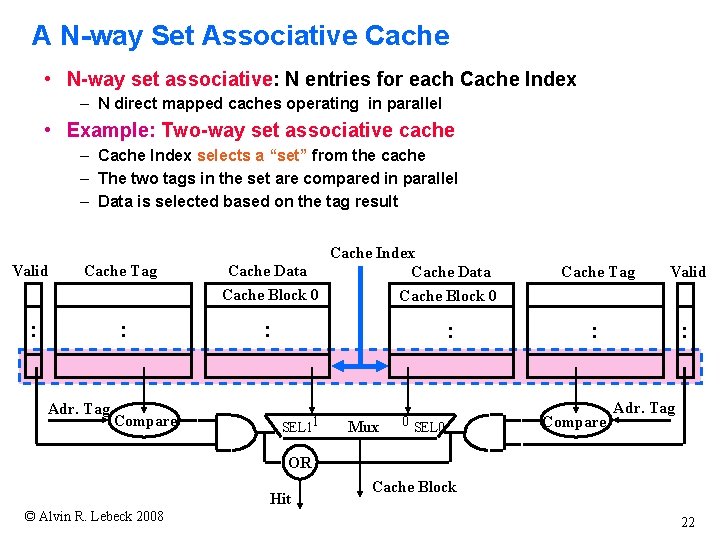
A N-way Set Associative Cache • N-way set associative: N entries for each Cache Index – N direct mapped caches operating in parallel • Example: Two-way set associative cache – Cache Index selects a “set” from the cache – The two tags in the set are compared in parallel – Data is selected based on the tag result Valid Cache Tag : : Adr. Tag Compare Cache Data Cache Block 0 Cache Index Cache Data Valid : : Cache Block 0 : : SEL 11 Cache Tag Mux 0 SEL 0 Compare Adr. Tag OR Hit © Alvin R. Lebeck 2008 Cache Block 22

Advantages of Set associative cache • Higher Hit rate for the same cache size. • Fewer Conflict Misses. • Can have a larger cache but keep the index smaller (same size as virtual page index) © Alvin R. Lebeck 2008 23

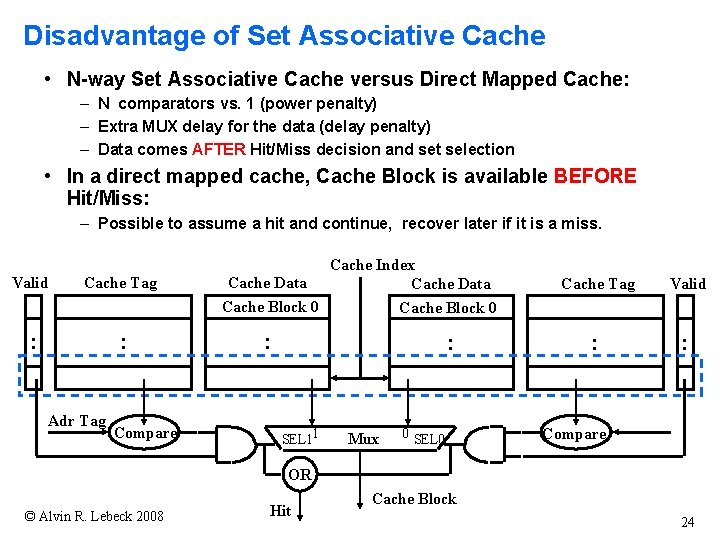
Disadvantage of Set Associative Cache • N-way Set Associative Cache versus Direct Mapped Cache: – N comparators vs. 1 (power penalty) – Extra MUX delay for the data (delay penalty) – Data comes AFTER Hit/Miss decision and set selection • In a direct mapped cache, Cache Block is available BEFORE Hit/Miss: – Possible to assume a hit and continue, recover later if it is a miss. Valid Cache Tag : : Adr Tag Compare Cache Index Cache Data Cache Block 0 : : SEL 11 Mux 0 SEL 0 Cache Tag Valid : : Compare OR © Alvin R. Lebeck 2008 Hit Cache Block 24

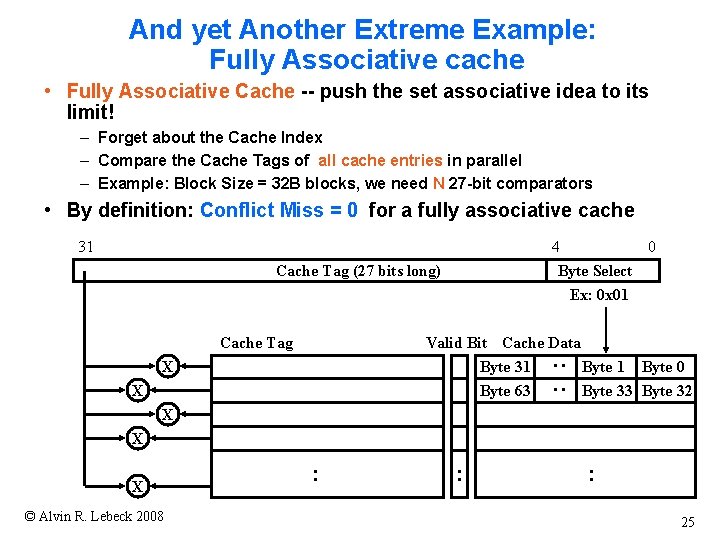
And yet Another Extreme Example: Fully Associative cache • Fully Associative Cache -- push the set associative idea to its limit! – Forget about the Cache Index – Compare the Cache Tags of all cache entries in parallel – Example: Block Size = 32 B blocks, we need N 27 -bit comparators • By definition: Conflict Miss = 0 for a fully associative cache 31 4 0 Byte Select Ex: 0 x 01 Cache Tag (27 bits long) Cache Tag Valid Bit Cache Data Byte 31 Byte 0 Byte 63 Byte 32 : : X X X © Alvin R. Lebeck 2008 : : : 25

Sources of Cache Misses • Compulsory (cold start or process migration, first reference): first access to a block – Miss in infinite cache – “Cold” fact of life: not a whole lot you can do about it – Prefetch, larger block gives implicit prefetch • Capacity: – Miss in Fully Associative cache with LRU replacement – Cache cannot contain all blocks access by the program – Solution: increase cache size • Conflict (collision): – Hit in Fully Associative, miss in Set-Associative – Multiple memory locations mapped to the same cache location – Solution 1: increase cache size – Solution 2: increase associativity • Invalidation: other process (e. g. , I/O) updates memory © Alvin R. Lebeck 2008 26

Sources of Cache Misses Direct Mapped Cache Size Compulsory Miss Big Same N-way Set Associative Medium Same Fully Associative Small Same Conflict Miss High Medium Zero Capacity Miss Low(er) Medium High Invalidation Miss Same/lower Note: If you are going to run “billions” of instruction, Compulsory Misses are insignificant. © Alvin R. Lebeck 2008 27

The Need to Make a Decision! • Direct Mapped Cache: – Each memory location can map to only 1 cache location (frame) – No need to make any decision : -) » Current item replaced the previous item in that cache location • N-way Set Associative Cache: – Each memory location have a choice of N cache frames • Fully Associative Cache: – Each memory location can be placed in ANY cache frame • Cache miss in a N-way Set Associative or Fully Associative Cache: – Bring in new block from memory – Throw out a cache block to make room for the new block – We need to make a decision on which block to throw out! © Alvin R. Lebeck 2008 28

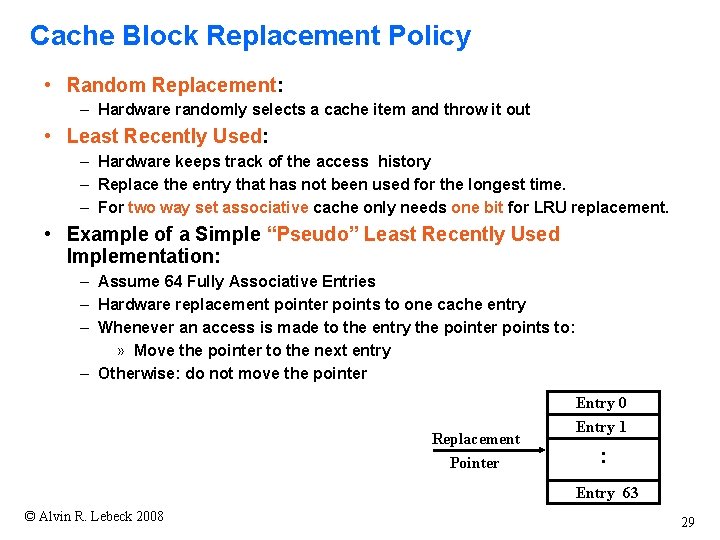
Cache Block Replacement Policy • Random Replacement: – Hardware randomly selects a cache item and throw it out • Least Recently Used: – Hardware keeps track of the access history – Replace the entry that has not been used for the longest time. – For two way set associative cache only needs one bit for LRU replacement. • Example of a Simple “Pseudo” Least Recently Used Implementation: – Assume 64 Fully Associative Entries – Hardware replacement pointer points to one cache entry – Whenever an access is made to the entry the pointer points to: » Move the pointer to the next entry – Otherwise: do not move the pointer Replacement Pointer Entry 0 Entry 1 : Entry 63 © Alvin R. Lebeck 2008 29

Cache Write Policy: Write Through versus Write Back • Cache read is much easier to handle than cache write: – Instruction cache is much easier to design than data cache • Cache write: – How do we keep data in the cache and memory consistent? • Two options (decision time again : -) – Write Back: write to cache only. Write the cache block to memory when that cache block is being replaced on a cache miss. » Need a “dirty bit” for each cache block » Greatly reduce the memory bandwidth requirement » Can buffer the data in a write-back buffer » Control can be complex – Write Through: write to cache and memory at the same time. » What!!! How can this be? Isn’t memory too slow for this? © Alvin R. Lebeck 2008 30

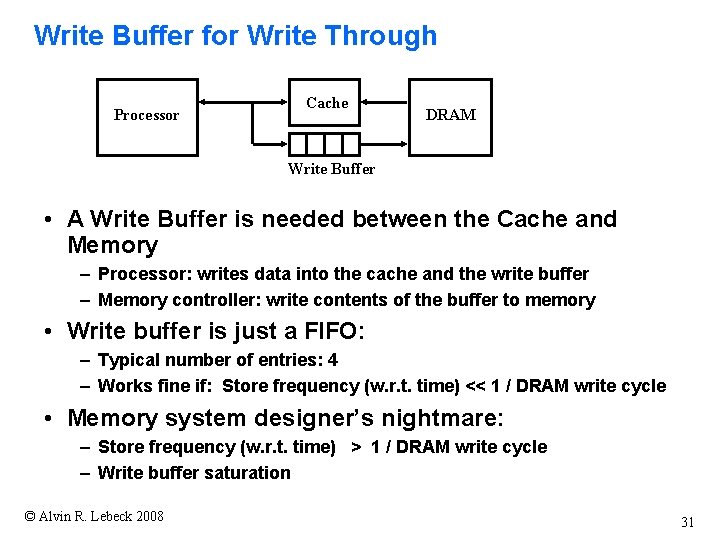
Write Buffer for Write Through Processor Cache DRAM Write Buffer • A Write Buffer is needed between the Cache and Memory – Processor: writes data into the cache and the write buffer – Memory controller: write contents of the buffer to memory • Write buffer is just a FIFO: – Typical number of entries: 4 – Works fine if: Store frequency (w. r. t. time) << 1 / DRAM write cycle • Memory system designer’s nightmare: – Store frequency (w. r. t. time) > 1 / DRAM write cycle – Write buffer saturation © Alvin R. Lebeck 2008 31

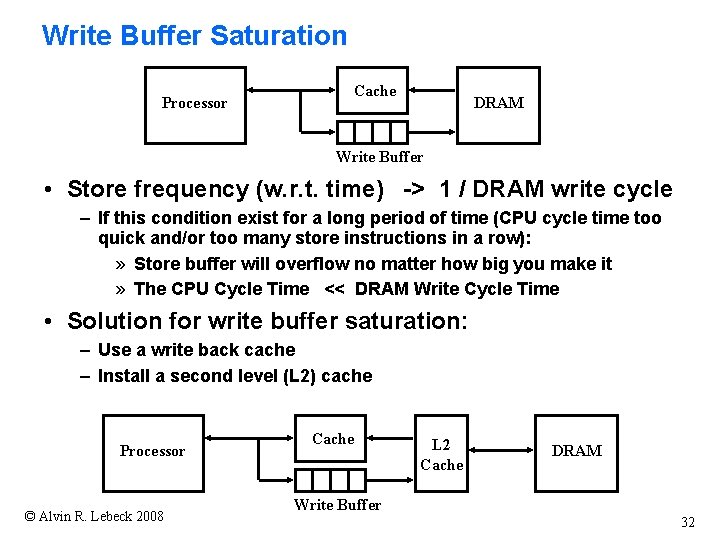
Write Buffer Saturation Processor Cache DRAM Write Buffer • Store frequency (w. r. t. time) -> 1 / DRAM write cycle – If this condition exist for a long period of time (CPU cycle time too quick and/or too many store instructions in a row): » Store buffer will overflow no matter how big you make it » The CPU Cycle Time << DRAM Write Cycle Time • Solution for write buffer saturation: – Use a write back cache – Install a second level (L 2) cache Processor © Alvin R. Lebeck 2008 Cache L 2 Cache DRAM Write Buffer 32

Write Policies • We know about write-through vs. write-back • Assume: a 16 -bit write to memory location 0 x 00 causes a cache miss. • Do we change the cache tag and update data in the block? Yes: Write Allocate No: Write No-Allocate • Do we fetch the other data in the block? Yes: Fetch-on-Write (usually do write-allocate) No: No-Fetch-on-Write • Write-around cache – Write-through no-write-allocate © Alvin R. Lebeck 2008 33

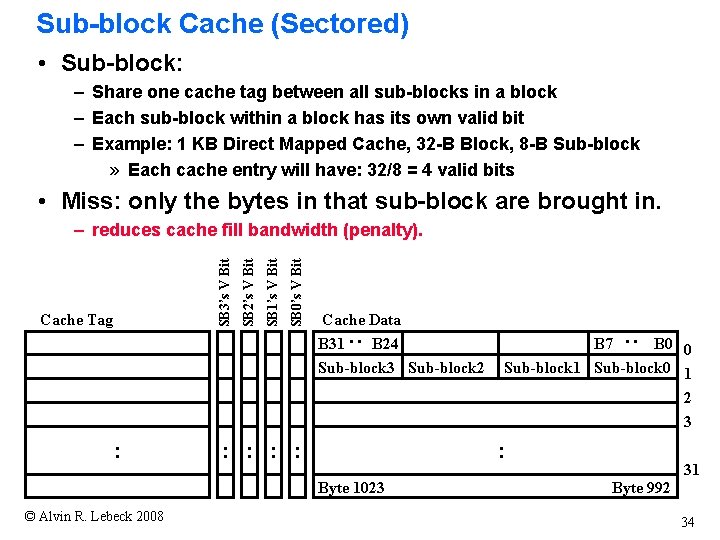
Sub-block Cache (Sectored) • Sub-block: – Share one cache tag between all sub-blocks in a block – Each sub-block within a block has its own valid bit – Example: 1 KB Direct Mapped Cache, 32 -B Block, 8 -B Sub-block » Each cache entry will have: 32/8 = 4 valid bits • Miss: only the bytes in that sub-block are brought in. : : Byte 1023 © Alvin R. Lebeck 2008 B 7 B 0 0 Sub-block 1 Sub-block 0 1 2 3 : Cache Data B 31 B 24 Sub-block 3 Sub-block 2 : SB 0’s V Bit SB 1’s V Bit Cache Tag SB 2’s V Bit SB 3’s V Bit – reduces cache fill bandwidth (penalty). 31 Byte 992 34

Review: Four Questions for Memory Hierarchy Designers • Q 1: Where can a block be placed in the upper level? (Block placement) – Fully Associative, Set Associative, Direct Mapped • Q 2: How is a block found if it is in the upper level? (Block identification) – Tag/Block • Q 3: Which block should be replaced on a miss? (Block replacement) – Random, LRU • Q 4: What happens on a write? (Write strategy) – Write Back or Write Through (with Write Buffer) © Alvin R. Lebeck 2008 CPS 220 35

Cache Performance CPU time = (CPU execution clock cycles + Memory stall clock cycles) x clock cycle time Memory stall clock cycles = (Reads x Read miss rate x Read miss penalty + Writes x Write miss rate x Write miss penalty) Memory stall clock cycles = Memory accesses x Miss rate x Miss penalty © Alvin R. Lebeck 2008 CPS 220 36

Cache Performance CPUtime = IC x (CPIexecution + (Mem accesses per instruction x Miss rate x Miss penalty)) x Clock cycle time hits are included in CPIexecution Misses per instruction = Memory accesses per instruction x Miss rate CPUtime = IC x (CPIexecution + Misses per instruction x Miss penalty) x Clock cycle time © Alvin R. Lebeck 2008 CPS 220 37

Example • • • Miss penalty 50 clocks Miss rate 2% Base CPI 2. 0 1. 33 references per instruction Compute the CPUtime • CPUtime = IC x (2. 0 + (1. 33 x 0. 02 x 50)) x Clock • CPUtime = IC x 3. 33 x Clock • So CPI increased from 2. 0 to 3. 33 with a 2% miss rate © Alvin R. Lebeck 2008 38

Example 2 • Two caches: both 64 KB, 32 byte blocks, miss penalty 70 ns, 1. 3 references per instruction, CPI 2. 0 w/ perfect cache • direct mapped – Cycle time 2 ns – Miss rate 1. 4% • 2 -way associative – Cycle time increases by 10% – Miss rate 1. 0% • Which is better? – Compute average memory access time – Compute CPU time © Alvin R. Lebeck 2008 39

Example 2 Continued • Ave Mem Acc Time = Hit time + (miss rate x miss penalty) – 1 -way: 2. 0 + (0. 014 x 70) = 2. 98 ns – 2 -way: 2. 2 + (0. 010 x 70) = 2. 90 ns • CPUtime = IC x CPIexec x Cycle – CPIexec = CPIbase + ((memacc/inst) x Miss rate x miss penalty) – Note: miss penalty x cycle time = 70 ns – 1 -way: IC x ((2. 0 x 2. 0) + (1. 3 x 0. 014 x 70)) = 5. 27 x IC – 2 -way: IC x ((2. 0 x 2. 2) + (1. 3 x 0. 010 x 70)) = 5. 31 x IC © Alvin R. Lebeck 2008 40