Memory COE 301 Computer Organization Dr Muhamed Mudawar

Memory COE 301 Computer Organization Dr. Muhamed Mudawar College of Computer Sciences and Engineering King Fahd University of Petroleum and Minerals

Presentation Outline v Random Access Memory and its Structure v Memory Hierarchy and the need for Cache Memory v The Basics of Caches v Cache Performance and Memory Stall Cycles v Improving Cache Performance v Multilevel Caches

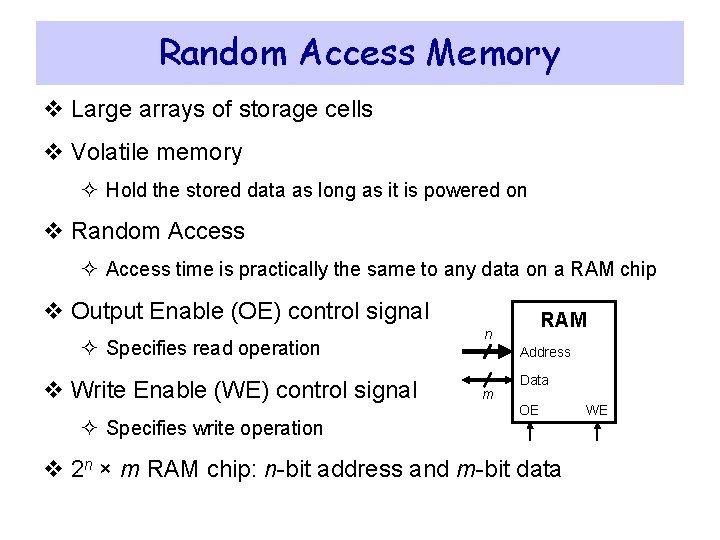
Random Access Memory v Large arrays of storage cells v Volatile memory ² Hold the stored data as long as it is powered on v Random Access ² Access time is practically the same to any data on a RAM chip v Output Enable (OE) control signal ² Specifies read operation v Write Enable (WE) control signal ² Specifies write operation RAM n Address m Data OE v 2 n × m RAM chip: n-bit address and m-bit data WE

Memory Technology v Static RAM (SRAM) for Cache ² Requires 6 transistors per bit ² Requires low power to retain bit v Dynamic RAM (DRAM) for Main Memory ² One transistor + capacitor per bit ² Must be re-written after being read ² Must also be periodically refreshed § Each row can be refreshed simultaneously ² Address lines are multiplexed § Upper half of address: Row Access Strobe (RAS) § Lower half of address: Column Access Strobe (CAS)

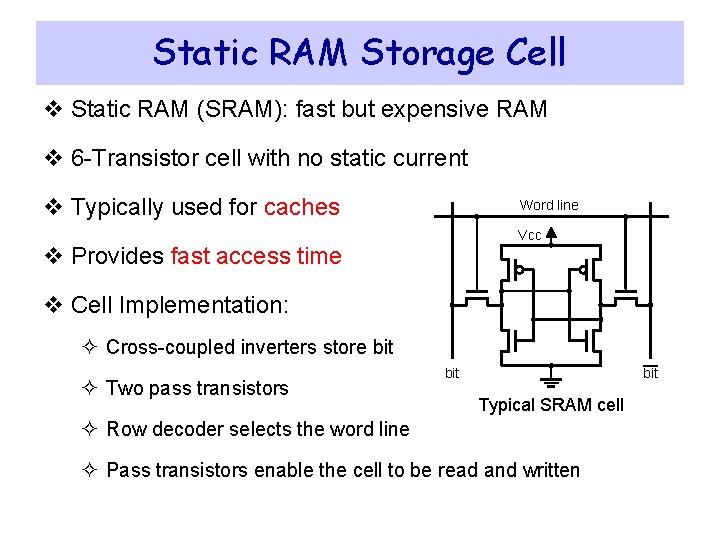
Static RAM Storage Cell v Static RAM (SRAM): fast but expensive RAM v 6 -Transistor cell with no static current v Typically used for caches Word line Vcc v Provides fast access time v Cell Implementation: ² Cross-coupled inverters store bit ² Two pass transistors bit Typical SRAM cell ² Row decoder selects the word line ² Pass transistors enable the cell to be read and written

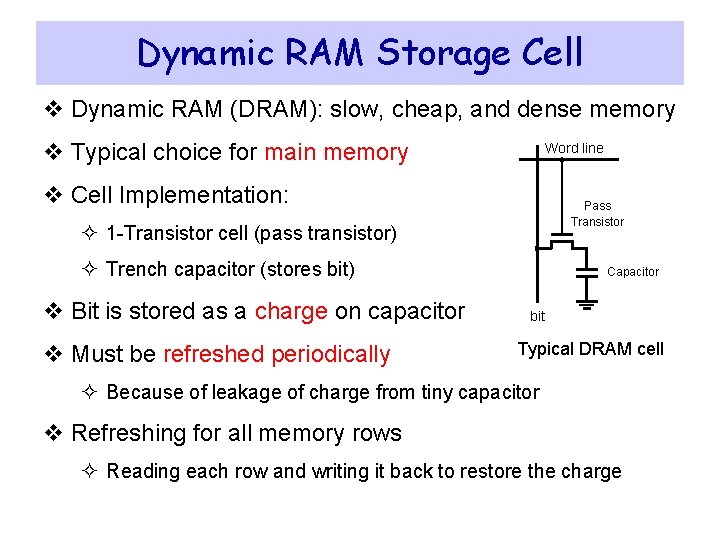
Dynamic RAM Storage Cell v Dynamic RAM (DRAM): slow, cheap, and dense memory v Typical choice for main memory Word line v Cell Implementation: Pass Transistor ² 1 -Transistor cell (pass transistor) ² Trench capacitor (stores bit) v Bit is stored as a charge on capacitor v Must be refreshed periodically Capacitor bit Typical DRAM cell ² Because of leakage of charge from tiny capacitor v Refreshing for all memory rows ² Reading each row and writing it back to restore the charge

Typical DRAM Packaging v 24 -pin dual in-line package for 16 Mbit = 222 4 memory Legend v 22 -bit address is divided into ² 11 -bit row address ² 11 -bit column address ² Interleaved on same address lines Ai CAS Dj NC OE RAS WE Address bit i Column address strobe Data bit j No connection Output enable Row address strobe Write enable Vss D 4 D 3 CAS OE A 9 A 8 A 7 A 6 A 5 A 4 Vss 24 23 22 21 20 19 18 17 16 15 14 13 1 2 3 4 5 6 7 8 9 10 11 12 Vcc D 1 D 2 WE RAS NC A 10 A 1 A 2 A 3 Vcc

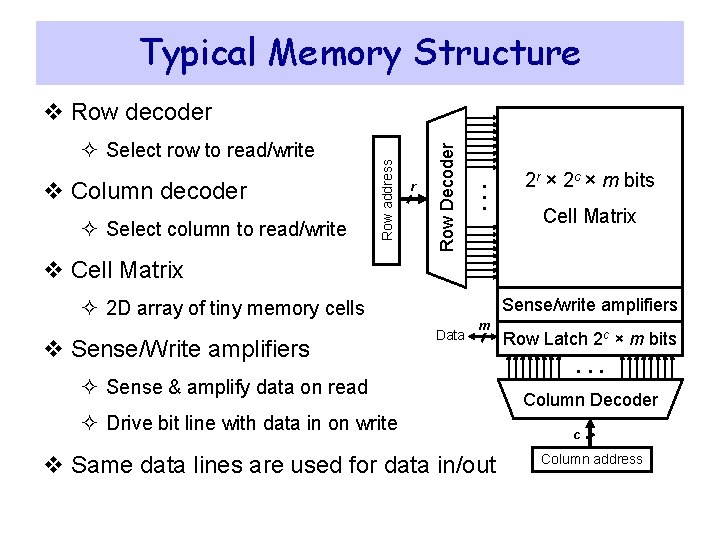
Typical Memory Structure ² Select column to read/write . . . v Column decoder r Row Decoder ² Select row to read/write Row address v Row decoder 2 r × 2 c × m bits Cell Matrix v Cell Matrix Sense/write amplifiers ² 2 D array of tiny memory cells v Sense/Write amplifiers Data m ² Sense & amplify data on read ² Drive bit line with data in on write v Same data lines are used for data in/out Row Latch 2 c × m bits . . . Column Decoder c Column address

DRAM Operation v Row Access (RAS) ² Latch and decode row address to enable addressed row ² Small change in voltage detected by sense amplifiers ² Latch whole row of bits ² Sense amplifiers drive bit lines to recharge storage cells v Column Access (CAS) read and write operation ² Latch and decode column address to select m bits ² m = 4, 8, 16, or 32 bits depending on DRAM package ² On read, send latched bits out to chip pins ² On write, charge storage cells to required value ² Can perform multiple column accesses to same row (burst mode)

Burst Mode Operation v Block Transfer ² Row address is latched and decoded ² A read operation causes all cells in a selected row to be read ² Selected row is latched internally inside the SDRAM chip ² Column address is latched and decoded ² Selected column data is placed in the data output register ² Column address is incremented automatically ² Multiple data items are read depending on the block length v Fast transfer of blocks between memory and cache v Fast transfer of pages between memory and disk

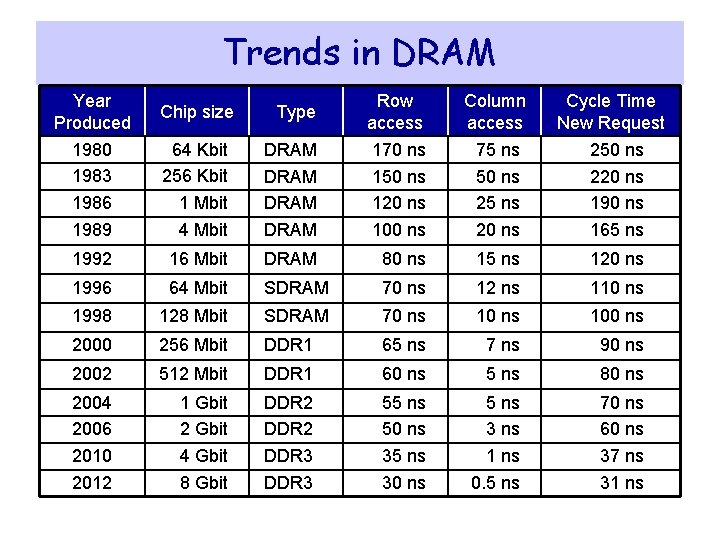
Trends in DRAM Year Produced Chip size Type Row access Column access 1980 1983 1986 1989 Cycle Time New Request 64 Kbit 256 Kbit 1 Mbit 4 Mbit DRAM 170 ns 150 ns 120 ns 100 ns 75 ns 50 ns 25 ns 20 ns 250 ns 220 ns 190 ns 165 ns 1992 16 Mbit DRAM 80 ns 15 ns 120 ns 1996 64 Mbit SDRAM 70 ns 12 ns 110 ns 1998 128 Mbit SDRAM 70 ns 100 ns 2000 256 Mbit DDR 1 65 ns 7 ns 90 ns 2002 512 Mbit DDR 1 60 ns 5 ns 80 ns 2004 2006 2010 2012 1 Gbit 2 Gbit 4 Gbit 8 Gbit DDR 2 DDR 3 55 ns 50 ns 35 ns 30 ns 5 ns 3 ns 1 ns 0. 5 ns 70 ns 60 ns 37 ns 31 ns

SDRAM and DDR SDRAM v SDRAM is Synchronous Dynamic RAM ² Added clock to DRAM interface v SDRAM is synchronous with the system clock ² Older DRAM technologies were asynchronous ² As system bus clock improved, SDRAM delivered higher performance than asynchronous DRAM v DDR is Double Data Rate SDRAM ² Like SDRAM, DDR is synchronous with the system clock, but the difference is that DDR reads data on both the rising and falling edges of the clock signal

Transfer Rates & Peak Bandwidth Standard Name Memory Bus Clock Millions Transfers per second Module Name Peak Bandwidth DDR-200 100 MHz 200 MT/s PC-1600 MB/s DDR-333 167 MHz 333 MT/s PC-2700 2667 MB/s DDR-400 200 MHz 400 MT/s PC-3200 MB/s DDR 2 -667 333 MHz 667 MT/s PC-5300 5333 MB/s DDR 2 -800 400 MHz 800 MT/s PC-6400 MB/s DDR 2 -1066 533 MHz 1066 MT/s PC-8500 8533 MB/s DDR 3 -1333 667 MHz 1333 MT/s PC-10600 10667 MB/s DDR 3 -1600 800 MHz 1600 MT/s PC-12800 MB/s DDR 4 -3200 1600 MHz 3200 MT/s PC-25600 MB/s v 1 Transfer = 64 bits = 8 bytes of data

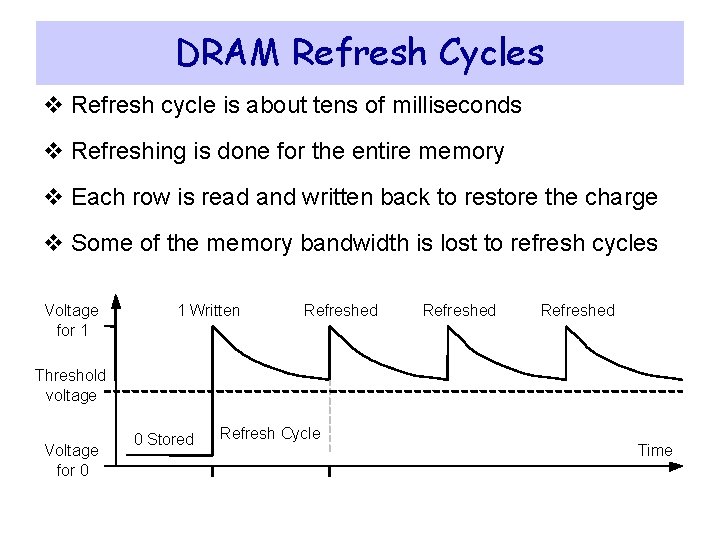
DRAM Refresh Cycles v Refresh cycle is about tens of milliseconds v Refreshing is done for the entire memory v Each row is read and written back to restore the charge v Some of the memory bandwidth is lost to refresh cycles Voltage for 1 1 Written Refreshed Threshold voltage Voltage for 0 0 Stored Refresh Cycle Time

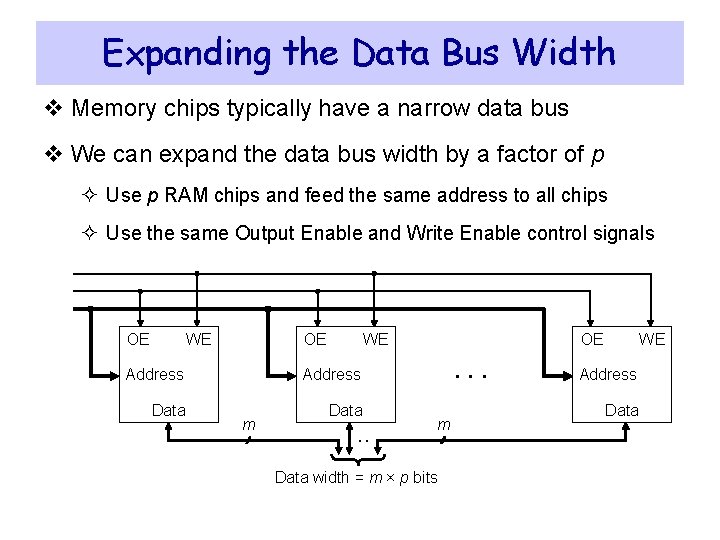
Expanding the Data Bus Width v Memory chips typically have a narrow data bus v We can expand the data bus width by a factor of p ² Use p RAM chips and feed the same address to all chips ² Use the same Output Enable and Write Enable control signals OE WE Address Data m . . OE . . . m Data width = m × p bits WE Address Data

Next. . . v Random Access Memory and its Structure v Memory Hierarchy and the need for Cache Memory v The Basics of Caches v Cache Performance and Memory Stall Cycles v Improving Cache Performance v Multilevel Caches

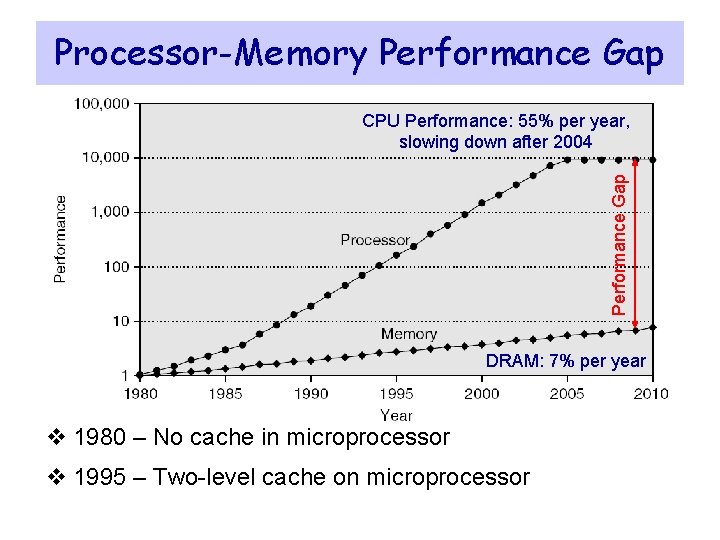
Processor-Memory Performance Gap CPU Performance: 55% per year, slowing down after 2004 DRAM: 7% per year v 1980 – No cache in microprocessor v 1995 – Two-level cache on microprocessor

The Need for Cache Memory v Widening speed gap between CPU and main memory ² Processor operation takes less than 1 ns ² Main memory requires more than 50 ns to access v Each instruction involves at least one memory access ² One memory access to fetch the instruction ² A second memory access for load and store instructions v Memory bandwidth limits the instruction execution rate v Cache memory can help bridge the CPU-memory gap v Cache memory is small in size but fast

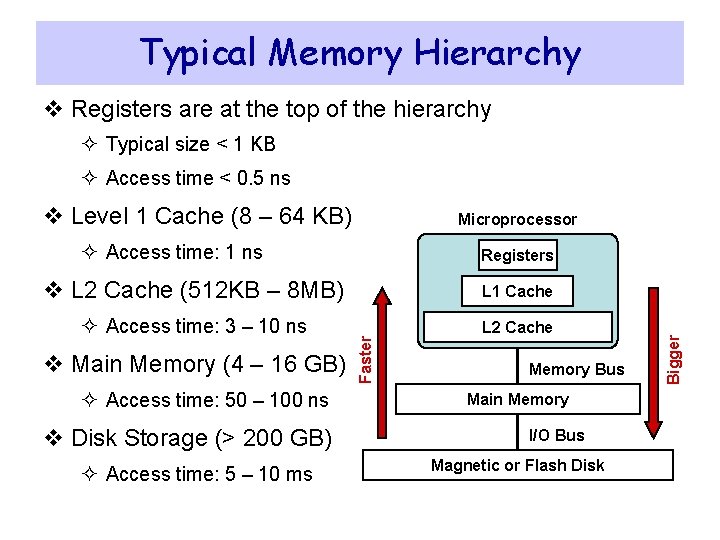
Typical Memory Hierarchy v Registers are at the top of the hierarchy ² Typical size < 1 KB ² Access time < 0. 5 ns v Level 1 Cache (8 – 64 KB) Microprocessor ² Access time: 1 ns L 1 Cache ² Access time: 3 – 10 ns L 2 Cache v Main Memory (4 – 16 GB) ² Access time: 50 – 100 ns v Disk Storage (> 200 GB) ² Access time: 5 – 10 ms Faster v L 2 Cache (512 KB – 8 MB) Memory Bus Main Memory I/O Bus Magnetic or Flash Disk Bigger Registers

Principle of Locality of Reference v Programs access small portion of their address space ² At any time, only a small set of instructions & data is needed v Temporal Locality (in time) ² If an item is accessed, probably it will be accessed again soon ² Same loop instructions are fetched each iteration ² Same procedure may be called and executed many times v Spatial Locality (in space) ² Tendency to access contiguous instructions/data in memory ² Sequential execution of Instructions ² Traversing arrays element by element

What is a Cache Memory ? v Small and fast (SRAM) memory technology ² Stores the subset of instructions & data currently being accessed v Used to reduce average access time to memory v Caches exploit temporal locality by … ² Keeping recently accessed data closer to the processor v Caches exploit spatial locality by … ² Moving blocks consisting of multiple contiguous words v Goal is to achieve ² Fast speed of cache memory access ² Balance the cost of the memory system

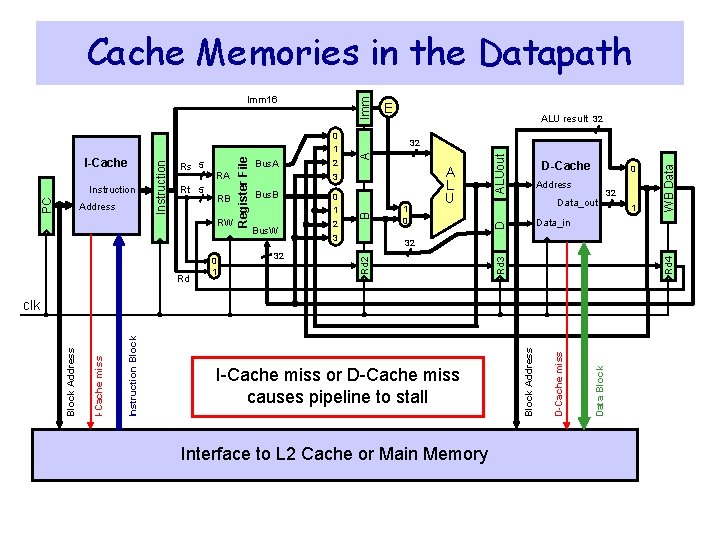
Cache Memories in the Datapath Imm Rd 0 1 Bus. W 32 0 1 2 3 1 0 D-Cache 0 Address Data_out 32 Interface to L 2 Cache or Main Memory Data Block D-Cache miss I-Cache miss or D-Cache miss causes pipeline to stall Block Address Instruction Block I-Cache miss 1 Data_in clk Block Address 32 WB Data Bus. B A L U ALUout A 3 Rd 4 RW 2 D RB Bus. A 32 B Address Rt 5 RA ALU result 32 Rd 2 PC Instruction Rs 5 Register File I-Cache Instruction 0 1 E Rd 3 Imm 16

Almost Everything is a Cache ! v In computer architecture, almost everything is a cache! v Registers: a cache on variables – software managed v First-level cache: a cache on second-level cache v Second-level cache: a cache on memory v Memory: a cache on hard disk ² Stores recent programs and their data ² Hard disk can be viewed as an extension to main memory v Branch target and prediction buffer ² Cache on branch target and prediction information

Next. . . v Random Access Memory and its Structure v Memory Hierarchy and the need for Cache Memory v The Basics of Caches v Cache Performance and Memory Stall Cycles v Improving Cache Performance v Multilevel Caches

Four Basic Questions on Caches v Q 1: Where can a block be placed in a cache? ² Block placement ² Direct Mapped, Set Associative, Fully Associative v Q 2: How is a block found in a cache? ² Block identification ² Block address, tag, index v Q 3: Which block should be replaced on a miss? ² Block replacement ² FIFO, Random, LRU v Q 4: What happens on a write? ² Write strategy ² Write Back or Write Through (with Write Buffer)

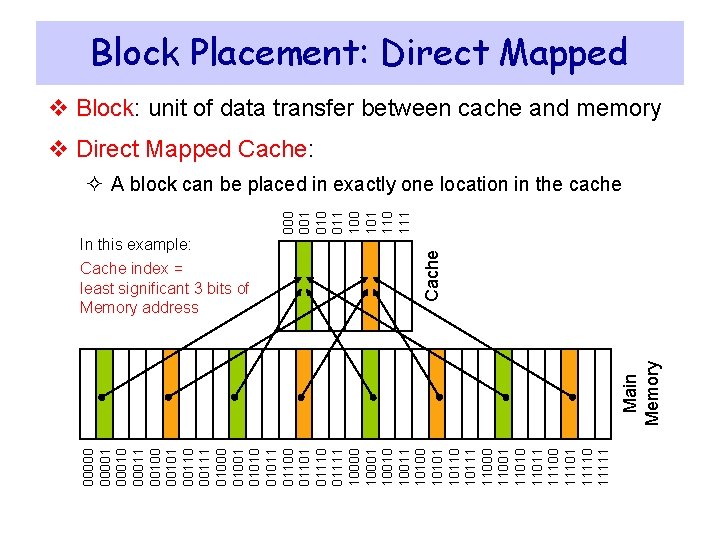
Block Placement: Direct Mapped v Block: unit of data transfer between cache and memory v Direct Mapped Cache: In this example: 000001 00010 00011 00100 00101 00110 00111 01000 01001 01010 01011 01100 01101 01110 01111 10000 10001 10010 10011 10100 10101 10110 10111 11000 11001 11010 11011 11100 11101 11110 11111 Main Memory Cache index = least significant 3 bits of Memory address Cache 000 001 010 011 100 101 110 111 ² A block can be placed in exactly one location in the cache

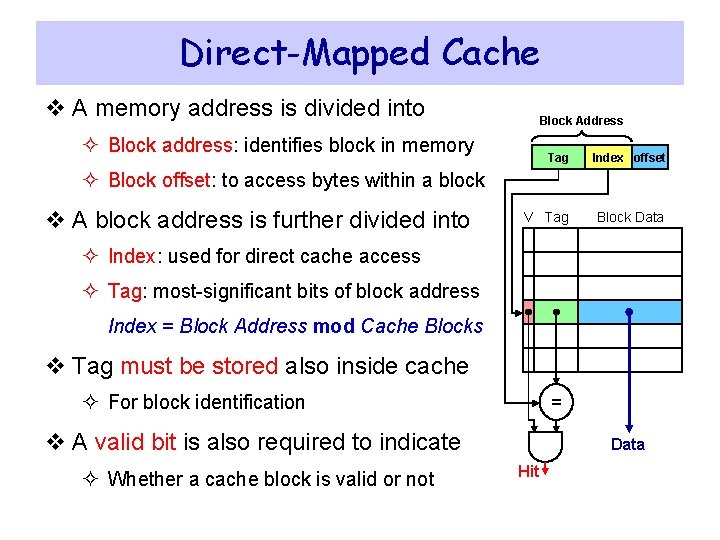
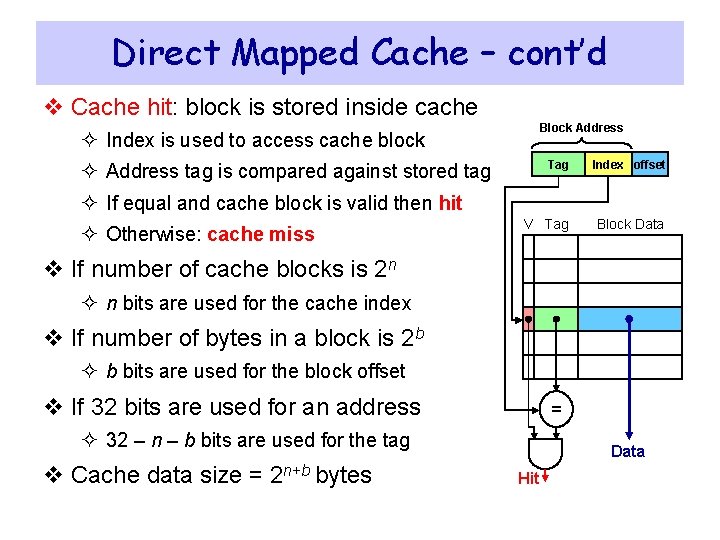
Direct-Mapped Cache v A memory address is divided into Block Address ² Block address: identifies block in memory Tag Index offset V Tag Block Data ² Block offset: to access bytes within a block v A block address is further divided into ² Index: used for direct cache access ² Tag: most-significant bits of block address Index = Block Address mod Cache Blocks v Tag must be stored also inside cache ² For block identification = v A valid bit is also required to indicate ² Whether a cache block is valid or not Data Hit

Direct Mapped Cache – cont’d v Cache hit: block is stored inside cache Block Address ² Index is used to access cache block Tag Index offset V Tag Block Data ² Address tag is compared against stored tag ² If equal and cache block is valid then hit ² Otherwise: cache miss v If number of cache blocks is 2 n ² n bits are used for the cache index v If number of bytes in a block is 2 b ² b bits are used for the block offset v If 32 bits are used for an address = ² 32 – n – b bits are used for the tag v Cache data size = 2 n+b bytes Data Hit

Mapping an Address to a Cache Block v Example ² Consider a direct-mapped cache with 256 blocks ² Block size = 16 bytes ² Compute tag, index, and byte offset of address: 0 x 01 FFF 8 AC v Solution ² 32 -bit address is divided into: Block Address 20 Tag 8 4 Index offset § 4 -bit byte offset field, because block size = 24 = 16 bytes § 8 -bit cache index, because there are 28 = 256 blocks in cache § 20 -bit tag field ² Byte offset = 0 x. C = 12 (least significant 4 bits of address) ² Cache index = 0 x 8 A = 138 (next lower 8 bits of address) ² Tag = 0 x 01 FFF (upper 20 bits of address)

Example on Cache Placement & Misses v Consider a small direct-mapped cache with 32 blocks ² Cache is initially empty, Block size = 16 bytes ² The following memory addresses (in decimal) are referenced: 1000, 1004, 1008, 2548, 2552, 2556. ² Map addresses to cache blocks and indicate whether hit or miss 23 v Solution: ² ² ² 1000 = 0 x 3 E 8 1004 = 0 x 3 EC 1008 = 0 x 3 F 0 2548 = 0 x 9 F 4 2552 = 0 x 9 F 8 2556 = 0 x 9 FC Tag 5 4 Index offset cache index = 0 x 1 E cache index = 0 x 1 F Miss (first access) Hit Miss (first access) Miss (different tag) Hit

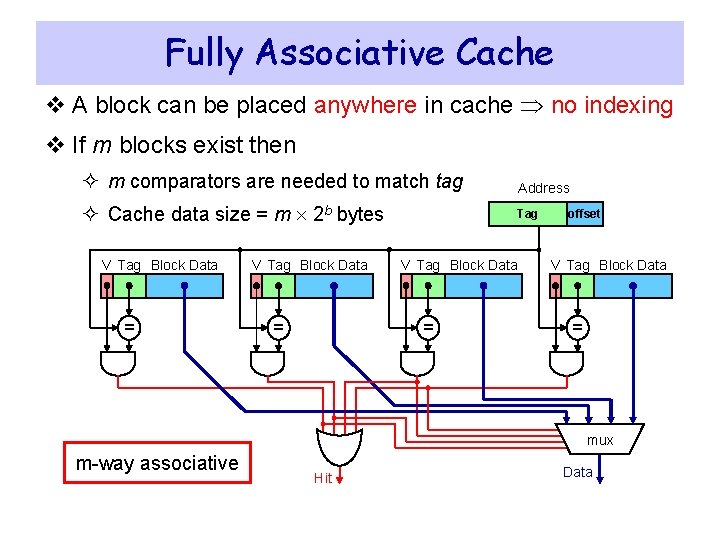
Fully Associative Cache v A block can be placed anywhere in cache no indexing v If m blocks exist then ² m comparators are needed to match tag Address ² Cache data size = m 2 b bytes Tag V Tag Block Data = offset V Tag Block Data = mux m-way associative Hit Data

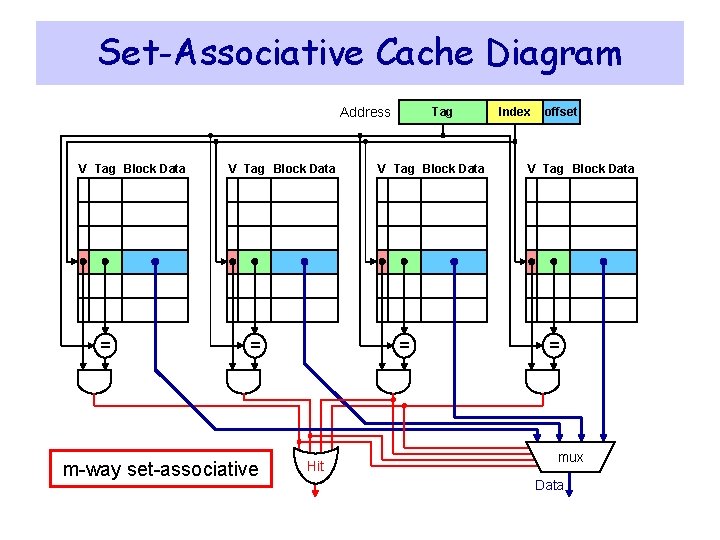
Set-Associative Cache v A set is a group of blocks that can be indexed v A block is first mapped onto a set ² Set index = Block address mod Number of sets in cache v If there are m blocks in a set (m-way set associative) then ² m tags are checked in parallel using m comparators v If 2 n sets exist then set index consists of n bits v Cache data size = m 2 n+b bytes (with 2 b bytes per block) ² Without counting tags and valid bits v A direct-mapped cache has one block per set (m = 1) v A fully-associative cache has one set (2 n = 1 or n = 0)

Set-Associative Cache Diagram Address V Tag Block Data = m-way set-associative Tag V Tag Block Data = Hit Index offset V Tag Block Data = mux Data

Write Policy v Write Through: ² Writes update cache and lower-level memory ² Cache control bit: only a Valid bit is needed ² Memory always has latest data, which simplifies data coherency ² Can always discard cached data when a block is replaced v Write Back: ² Writes update cache only ² Cache control bits: Valid and Modified bits are required ² Modified cached data is written back to memory when replaced ² Multiple writes to a cache block require only one write to memory ² Uses less memory bandwidth than write-through and less power ² However, more complex to implement than write through

Write Miss Policy v What happens on a write miss? v Write Allocate: ² Allocate new block in cache ² Write miss acts like a read miss, block is fetched and updated v No Write Allocate: ² Send data to lower-level memory ² Cache is not modified v Typically, write back caches use write allocate ² Hoping subsequent writes will be captured in the cache v Write-through caches often use no-write allocate ² Reasoning: writes must still go to lower level memory

Write Buffer v Decouples the CPU write from the memory bus writing ² Permits writes to occur without stall cycles until buffer is full v Write-through: all stores are sent to lower level memory ² Write buffer eliminates processor stalls on consecutive writes v Write-back: modified blocks are written when replaced ² Write buffer is used for evicted blocks that must be written back v The address and modified data are written in the buffer ² The write is finished from the CPU perspective ² CPU continues while the write buffer prepares to write memory v If buffer is full, CPU stalls until buffer has an empty entry

What Happens on a Cache Miss? v Cache sends a miss signal to stall the processor v Decide which cache block to allocate/replace ² One choice only when the cache is directly mapped ² Multiple choices for set-associative or fully-associative cache v Transfer the block from lower level memory to this cache ² Set the valid bit and the tag field from the upper address bits v If block to be replaced is modified then write it back ² Modified block is moved into a Write Buffer ² Otherwise, block to be replaced can be simply discarded v Restart the instruction that caused the cache miss v Miss Penalty: clock cycles to process a cache miss

Replacement Policy v Which block to be replaced on a cache miss? v No selection alternatives for direct-mapped caches v m blocks per set to choose from for associative caches v Random replacement ² Candidate blocks are randomly selected ² One counter for all sets (0 to m – 1): incremented on every cycle ² On a cache miss replace block specified by counter v First In First Out (FIFO) replacement ² Replace oldest block in set ² One counter per set (0 to m – 1): specifies oldest block to replace ² Counter is incremented on a cache miss

Replacement Policy – cont’d v Least Recently Used (LRU) ² Replace block that has been unused for the longest time ² Order blocks within a set from least to most recently used ² Update ordering of blocks on each cache hit ² With m blocks per set, there are m! possible permutations v Pure LRU is too costly to implement when m > 2 ² m = 2, there are 2 permutations only (a single bit is needed) ² m = 4, there are 4! = 24 possible permutations ² LRU approximation is used in practice v For large m > 4, Random replacement can be as effective as LRU

Comparing Random, FIFO, and LRU v Data cache misses per 1000 instructions ² 10 SPEC 2000 benchmarks on Alpha processor ² Block size of 64 bytes ² LRU and FIFO outperforming Random for a small cache ² Little difference between LRU and Random for a large cache v LRU is expensive for large associativity (# blocks per set) v Random is the simplest to implement in hardware 2 -way Size LRU 4 -way Rand FIFO LRU 8 -way Rand FIFO LRU Rand FIFO 16 KB 114. 1 117. 3 115. 5 111. 7 115. 1 113. 3 109. 0 111. 8 110. 4 64 KB 103. 4 104. 3 103. 9 102. 4 102. 3 103. 1 99. 7 100. 5 100. 3 92. 2 92. 1 256 KB 92. 1 92. 5

Next. . . v Random Access Memory and its Structure v Memory Hierarchy and the need for Cache Memory v The Basics of Caches v Cache Performance and Memory Stall Cycles v Improving Cache Performance v Multilevel Caches

Hit Rate and Miss Rate v Hit Rate = Hits / (Hits + Misses) v Miss Rate = Misses / (Hits + Misses) v I-Cache Miss Rate = Miss rate in the Instruction Cache v D-Cache Miss Rate = Miss rate in the Data Cache v Example: ² Out of 1000 instructions fetched, 150 missed in the I-Cache ² 25% are load-store instructions, 50 missed in the D-Cache ² What are the I-cache and D-cache miss rates? v I-Cache Miss Rate = 150 / 1000 = 15% v D-Cache Miss Rate = 50 / (25% × 1000) = 50 / 250 = 20%

Memory Stall Cycles v The processor stalls on a Cache miss ² When fetching instructions from the Instruction Cache (I-cache) ² When loading or storing data into the Data Cache (D-cache) Memory stall cycles = Combined Misses Miss Penalty v Miss Penalty: clock cycles to process a cache miss Combined Misses = I-Cache Misses + D-Cache Misses I-Cache Misses = I-Count × I-Cache Miss Rate D-Cache Misses = LS-Count × D-Cache Miss Rate LS-Count (Load & Store) = I-Count × LS Frequency v Cache misses are often reported per thousand instructions

Memory Stall Cycles Per Instruction v Memory Stall Cycles Per Instruction = Combined Misses Per Instruction × Miss Penalty v Miss Penalty is assumed equal for I-cache & D-cache v Miss Penalty is assumed equal for Load and Store v Combined Misses Per Instruction = I-Cache Miss Rate + LS Frequency × D-Cache Miss Rate v Therefore, Memory Stall Cycles Per Instruction = I-Cache Miss Rate × Miss Penalty + LS Frequency × D-Cache Miss Rate × Miss Penalty

Example on Memory Stall Cycles v Consider a program with the given characteristics ² Instruction count (I-Count) = 106 instructions ² 30% of instructions are loads and stores ² D-cache miss rate is 5% and I-cache miss rate is 1% ² Miss penalty is 100 clock cycles for instruction and data caches ² Compute combined misses per instruction and memory stall cycles v Combined misses per instruction in I-Cache and D-Cache ² 1% + 30% 5% = 0. 025 combined misses per instruction ² Equal to 25 misses per 1000 instructions v Memory stall cycles ² 0. 025 100 (miss penalty) = 2. 5 stall cycles per instruction ² Total memory stall cycles = 106 2. 5 = 2, 500, 000

CPU Time with Memory Stall Cycles CPU Time = I-Count × CPIMemory. Stalls × Clock Cycle CPIMemory. Stalls = CPIPerfect. Cache + Mem Stalls per Instruction v CPIPerfect. Cache = CPI for ideal cache (no cache misses) v CPIMemory. Stalls = CPI in the presence of memory stalls v Memory stall cycles increase the CPI

Example on CPI with Memory Stalls v A processor has CPI of 1. 5 without any memory stalls ² Cache miss rate is 2% for instruction and 5% for data ² 20% of instructions are loads and stores ² Cache miss penalty is 100 clock cycles for I-cache and D-cache v What is the impact on the CPI? v Answer: Instruction data Mem Stalls per Instruction = 0. 02× 100 + 0. 2× 0. 05× 100 = 3 CPIMemory. Stalls = 1. 5 + 3 = 4. 5 cycles per instruction CPIMemory. Stalls / CPIPerfect. Cache = 4. 5 / 1. 5 = 3 Processor is 3 times slower due to memory stall cycles CPINo. Cache = 1. 5 + (1 + 0. 2) × 100 = 121. 5 (a lot worse)

Average Memory Access Time v Average Memory Access Time (AMAT) AMAT = Hit time + Miss rate × Miss penalty v Time to access a cache for both hits and misses v Example: Find the AMAT for a cache with ² Cache access time (Hit time) of 1 cycle = 2 ns ² Miss penalty of 20 clock cycles ² Miss rate of 0. 05 per access v Solution: AMAT = 1 + 0. 05 × 20 = 2 cycles = 4 ns Without the cache, AMAT will be equal to Miss penalty = 20 cycles

Next. . . v Random Access Memory and its Structure v Memory Hierarchy and the need for Cache Memory v The Basics of Caches v Cache Performance and Memory Stall Cycles v Improving Cache Performance v Multilevel Caches

Improving Cache Performance v Average Memory Access Time (AMAT) AMAT = Hit time + Miss rate * Miss penalty v Used as a framework for optimizations v Reduce the Hit time ² Small and simple caches v Reduce the Miss Rate ² Larger cache size, higher associativity, and larger block size v Reduce the Miss Penalty ² Multilevel caches

Small and Simple Caches v Hit time is critical: affects the processor clock cycle ² Fast clock rate demands small and simple L 1 cache designs v Small cache reduces the indexing time and hit time ² Indexing a cache represents a time consuming portion ² Tag comparison also adds to this hit time v Direct-mapped overlaps tag check with data transfer ² Associative cache uses additional mux and increases hit time v Size of L 1 caches has not increased much ² L 1 caches are the same size on Alpha 21264 and 21364 ² Same also on Ultra. Sparc II and III, AMD K 6 and Athlon ² Reduced from 16 KB in Pentium III to 8 KB in Pentium 4

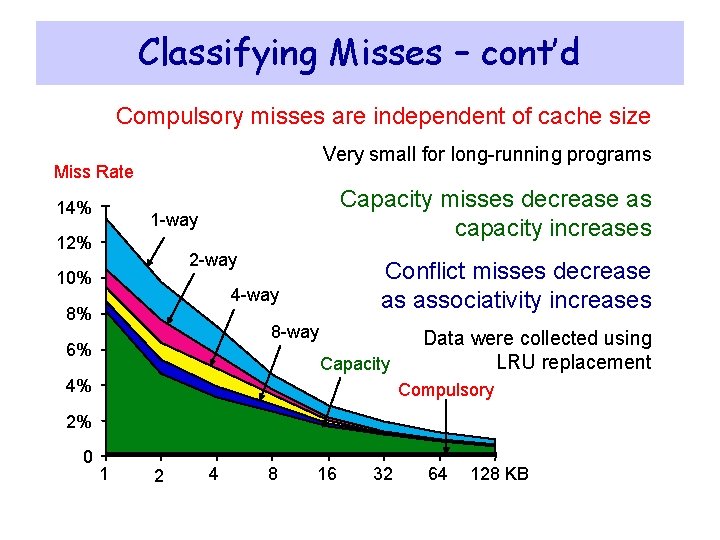
Classifying Misses – Three Cs v Conditions under which misses occur v Compulsory: program starts with no block in cache ² Also called cold start misses ² Misses that would occur even if a cache has infinite size v Capacity: misses happen because cache size is finite ² Blocks are replaced and then later retrieved ² Misses that would occur in a fully associative cache of a finite size v Conflict: misses happen because of limited associativity ² Limited number of blocks per set ² Non-optimal replacement algorithm

Classifying Misses – cont’d Compulsory misses are independent of cache size Very small for long-running programs Miss Rate 14% Capacity misses decrease as capacity increases 1 -way 12% 2 -way 10% Conflict misses decrease as associativity increases 4 -way 8% 8 -way 6% Capacity 4% Data were collected using LRU replacement Compulsory 2% 0 1 2 4 8 16 32 64 128 KB

Larger Size and Higher Associativity v Increasing cache size reduces capacity misses v It also reduces conflict misses ² Larger cache size spreads out references to more blocks v Drawbacks: longer hit time and higher cost v Larger caches are especially popular as 2 nd level caches v Higher associativity also improves miss rates ² Eight-way set associative is as effective as a fully associative

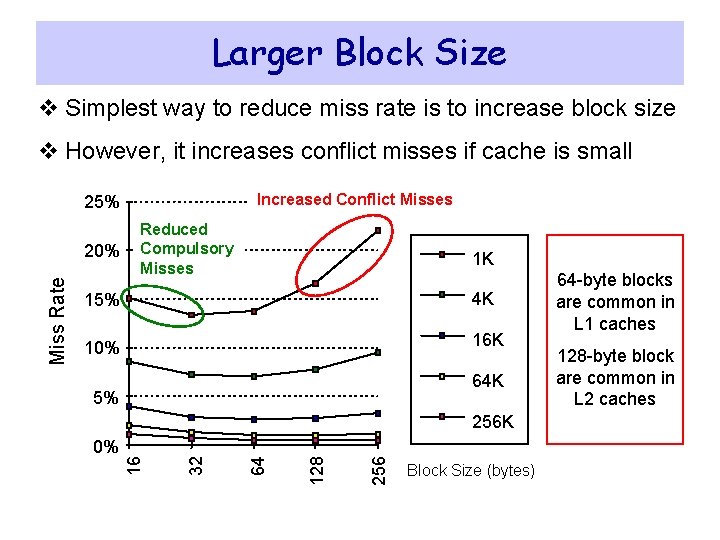
Larger Block Size v Simplest way to reduce miss rate is to increase block size v However, it increases conflict misses if cache is small Increased Conflict Misses 25% 1 K 15% 4 K 10% 16 K 64 K 5% 256 128 64 0% 32 256 K 16 Miss Rate 20% Reduced Compulsory Misses Block Size (bytes) 64 -byte blocks are common in L 1 caches 128 -byte block are common in L 2 caches

Next. . . v Random Access Memory and its Structure v Memory Hierarchy and the need for Cache Memory v The Basics of Caches v Cache Performance and Memory Stall Cycles v Improving Cache Performance v Multilevel Caches

Multilevel Caches v Top level cache should be kept small to ² Keep pace with processor speed v Adding another cache level ² Can reduce the memory gap ² Can reduce memory bus loading v Local miss rate I-Cache D-Cache Unified L 2 Cache Main Memory ² Number of misses in a cache / Memory accesses to this cache ² Miss Rate. L 1 for L 1 cache, and Miss Rate. L 2 for L 2 cache v Global miss rate Number of misses in a cache / Memory accesses generated by CPU Miss Rate. L 1 for L 1 cache, and Miss Rate. L 1 Miss Rate. L 2 for L 2 cache

Power 7 On-Chip Caches [IBM 2010] 32 KB I-Cache/core 32 KB D-Cache/core 3 -cycle latency 256 KB Unified L 2 Cache/core 8 -cycle latency 32 MB Unified Shared L 3 Cache Embedded DRAM 25 -cycle latency to local slice

Multilevel Cache Policies v Multilevel Inclusion ² L 1 cache data is always present in L 2 cache ² A miss in L 1, but a hit in L 2 copies block from L 2 to L 1 ² A miss in L 1 and L 2 brings a block into L 1 and L 2 ² A write in L 1 causes data to be written in L 1 and L 2 ² Typically, write-through policy is used from L 1 to L 2 ² Typically, write-back policy is used from L 2 to main memory § To reduce traffic on the memory bus ² A replacement or invalidation in L 2 must be propagated to L 1

Multilevel Cache Policies – cont’d v Multilevel exclusion ² L 1 data is never found in L 2 cache – Prevents wasting space ² Cache miss in L 1, but a hit in L 2 results in a swap of blocks ² Cache miss in both L 1 and L 2 brings the block into L 1 only ² Block replaced in L 1 is moved into L 2 ² Example: AMD Athlon v Same or different block size in L 1 and L 2 caches ² Choosing a larger block size in L 2 can improve performance ² However different block sizes complicates implementation ² Pentium 4 has 64 -byte blocks in L 1 and 128 -byte blocks in L 2