Membrane Properties chemical and electrical properties of biological

Membrane Properties chemical and electrical properties of biological membranes Jim Huettner

Lecture Overview • • Selective permeability Osmolarity and osmotic pressure Ionic gradients Electrical properties: resistance and capacitance Electrochemical equilibrium Environmental change GHK equation Intro to simulation

Membranes are Selective Barriers Cell membranes exhibit greater permeability to water than synthetic bilayers Alberts et al. , 6 th ed.

Relative Scale of Permeability Alberts et al. , 6 th ed.

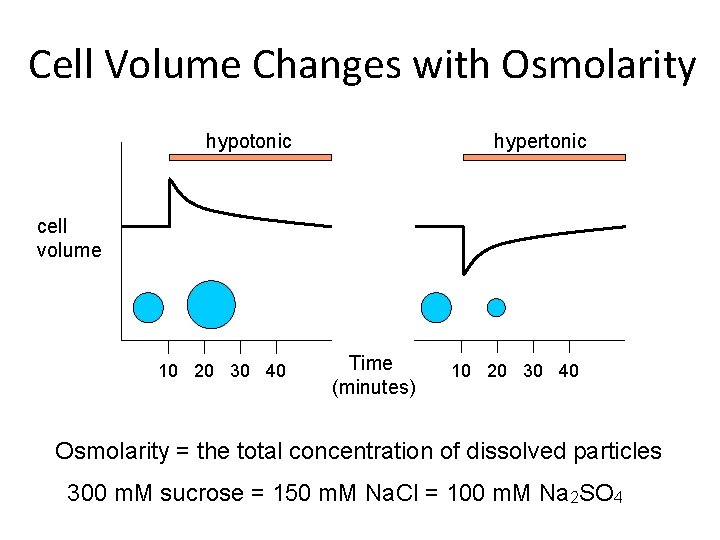
Cell Volume Changes with Osmolarity hypotonic hypertonic cell volume 10 20 30 40 Time (minutes) 10 20 30 40 Osmolarity = the total concentration of dissolved particles 300 m. M sucrose = 150 m. M Na. Cl = 100 m. M Na 2 SO 4

Tonicity v. s. Osmolarity = [dissolved particles] (physical chemistry) Tonicity = effective osmotic pressure relative to blood plasma (cell physiology – depends on permeability) 150 m. M Na. Cl – isotonic, isosmotic 10 m. M Et. OH – hypo osmotic and hypotonic Both together – isotonic, hyperosmotic van’t Hoff Formula: p = s. RT*(C 2 – C 1) osmotic pressure (p) is proportional to the difference in concentration, s is an index of impermeability

Ion Concentrations Na 117 K 3 Cl 120 Anions 0 Total 240 [+ charge] = [- charge] 0 m. V Na 30 K 90 Cl 4 Anions 116 Total 240 [+ charge] = [- charge] -89 m. V

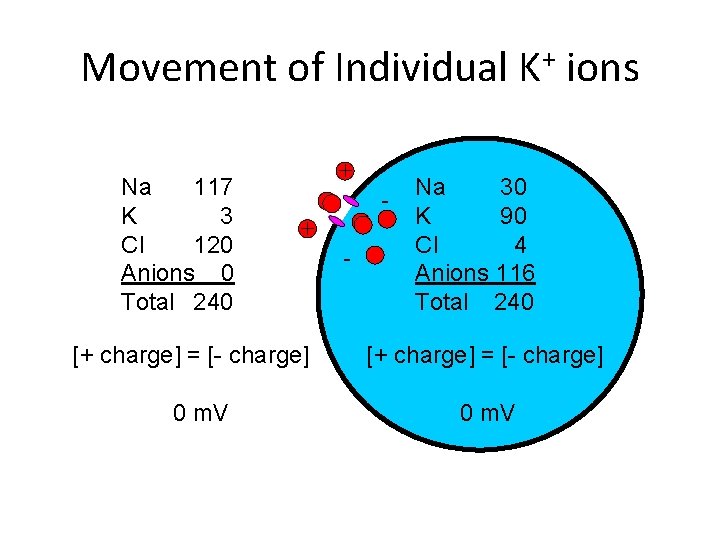
Movement of Individual K+ ions Na 117 K 3 Cl 120 Anions 0 Total 240 + + [+ charge] = [- charge] 0 m. V - Na 30 K 90 Cl 4 Anions 116 Total 240 [+ charge] = [- charge] 0 m. V

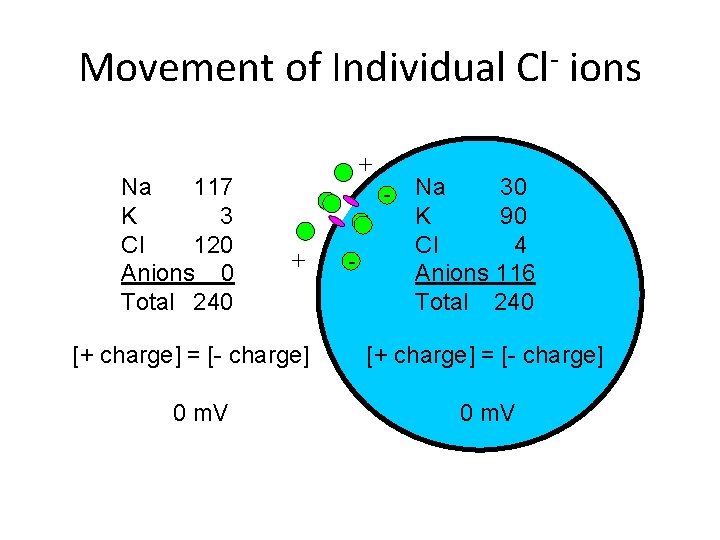
Movement of Individual Cl ions Na 117 K 3 Cl 120 Anions 0 Total 240 + + [+ charge] = [- charge] 0 m. V - Na 30 K 90 Cl 4 Anions 116 Total 240 [+ charge] = [- charge] 0 m. V

Voltage • Measures the difference in potential energy experienced by a charged particle in two locations. It is the work required to move a charge from point A to point B. V = Joules / Coulomb = Volts (V) • Separation of + and – charges produces a potential difference or voltage. • To keep the charges apart, they must be on opposite sides of an insulating barrier.

Capacitance • Measures how much charge must be separated to give a particular voltage: C (Farads) = Q (Coulombs) / V (Volts) • The cell membrane with dissolved ions on both sides acts as an electrical capacitor. By separating cations (+) and anions ( ) across the membrane you develop a potential difference (voltage) from one side to the other. The lipid bilayer of most cells has a specific capacitance of 1. 0 µFarad / cm 2.

Sample Problem • How many ions must cross the membrane of a spherical cell 50 µm in diameter (r = 25 µm) to create a membrane potential of – 89 m. V? Q (Coulombs) = C (Farads) * V (Volts) Specific Capacitance = 1. 0 µFarad / cm 2 Surface area = 4 p r 2 Faraday’s Constant = 9. 648 x 104 Coulombs / mole Avogadro’s # = 6. 022 x 1023 ions / mole

Calculations Area = 4 p r 2 1 Q=C*V = 4 p (25 x 10 4 cm)2 = 78. 5 x 10 12 Farads * 0. 089 Volts = 7. 85 x 10 5 cm 2 = 7 x 10 12 Coulombs 2 = 78. 5 x 10 6 µFarads = 78. 5 x 10 12 Farads Þ 7 x 10 -12 Coulombs / 9. 65 x 104 Coulombs per mole = 7. 3 x 10 -17 moles of ions must cross the membrane = 0. 073 femptomoles or ~ 44 x 106 ions 3

Types of Energy • • • Mechanical Energy: Hydraulic Energy: Gravitational Energy: Electrical Energy: Chemical Energy: Force * Distance Pressure * Volume Mass * g * height Potential (Volts) * Charge (Coulombs) R * T * ln [C] Chemical energy depends on the ability of a substance to react, which depends on concentration and temperature Charged particles in solution have chemical and electrical energy Electrochemical Energy: R * T * ln [C] + q * V

The Nernst Equation Calculates the membrane potential at which an ion will be in electrochemical equilibrium. At this potential: total energy inside = total energy outside Electrical Energy Term: z * F * V Chemical Energy Term: R * T * ln [Ion] Z is the charge, 1 for Na+ and K+, 2 for Ca 2+ and Mg 2+, 1 for Cl F is Faraday’s Constant = 9. 648 x 104 Coulombs / mole R is the gas constant = 8. 315 Joules / °Kelvin * mole T is the temperature in °Kelvin

Nernst Equation Derivation z. F * Vin + RT * ln [K+]in = z. F * Vout + RT * ln [K+]out z. F (Vin – Vout) = RT (ln [K+]out – ln [K+]in) EK = Vin – Vout = (RT / z. F) ln ([K+]out / [K+]in) EK = 2. 303 (RT / F) * log 10 ([K+]out / [K+]in) In General: Eion = (60 m. V / z) * log ([ion]out / [ion]in) @ 30°

Nernst Potential Calculations • First K and Cl EK = 60 m. V log (3 / 90) = 60 * 1. 477 = 89 m. V ECl = (60 m. V / 1) log (120 / 4) = 60 * 1. 477 = 89 m. V Both Cl and K are at electrochemical equilibrium at 89 m. V • Now for Sodium ENa = 60 m. V log (117 / 30) = 60 * 0. 591 = +36 m. V When Vm = 89 m. V, both the concentration gradient and electrical gradient for Na are from outside to inside

At Electrochemical Equilibrium: • The concentration gradient for the ion is exactly balanced by the electrical gradient • There is no net flux of the ion • There is no requirement for an energy driven pump to maintain the concentration gradient • Any ion not already at electrochemical equilibrium will flow toward it, if there is a way to cross the membrane

Ion Concentrations Na 117 K 3 Cl 120 Anions 0 Total 240 [+ charge] = [- charge] 0 m. V Na 30 K 90 Cl 4 Anions 116 Total 240 [+ charge] = [- charge] -89 m. V

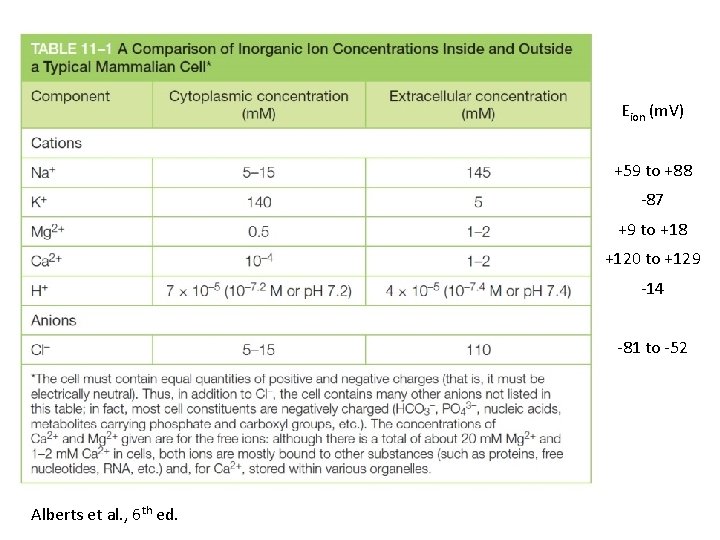
Eion (m. V) +59 to +88 87 +9 to +18 +120 to +129 14 81 to 52 Alberts et al. , 6 th ed.

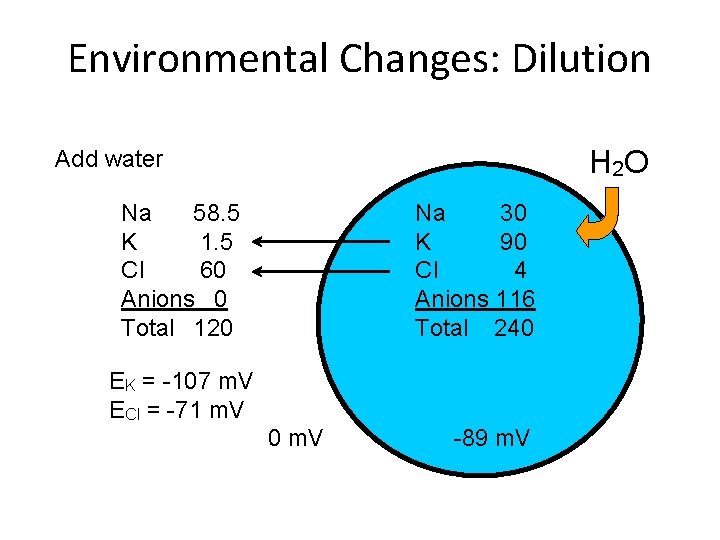
Environmental Changes: Dilution H 2 O Add water Na 58. 5 K 1. 5 Cl 60 Anions 0 Total 120 Na 30 K 90 Cl 4 Anions 116 Total 240 EK = -107 m. V ECl = -71 m. V 0 m. V -89 m. V

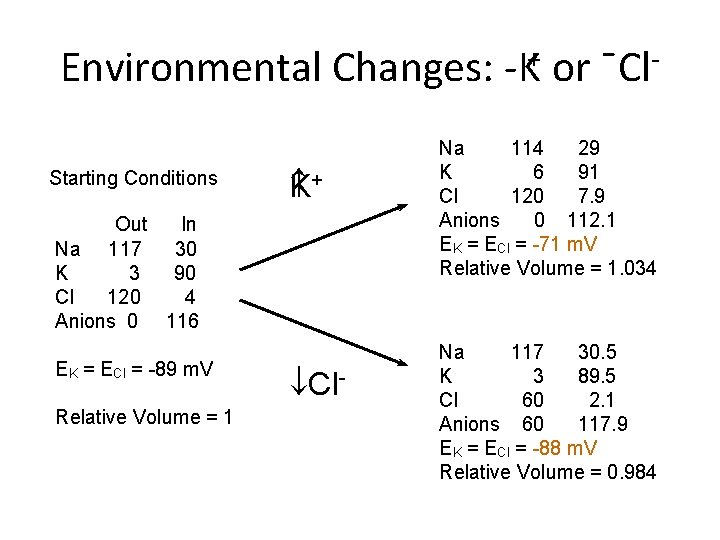
Environmental Changes: K+ or ¯Cl Starting Conditions + K Out In Na 117 30 K 3 90 Cl 120 4 Anions 0 116 EK = ECl = -89 m. V Relative Volume = 1 ¯Cl- Na 114 29 K 6 91 Cl 120 7. 9 Anions 0 112. 1 EK = ECl = -71 m. V Relative Volume = 1. 034 Na 117 30. 5 K 3 89. 5 Cl 60 2. 1 Anions 60 117. 9 EK = ECl = -88 m. V Relative Volume = 0. 984

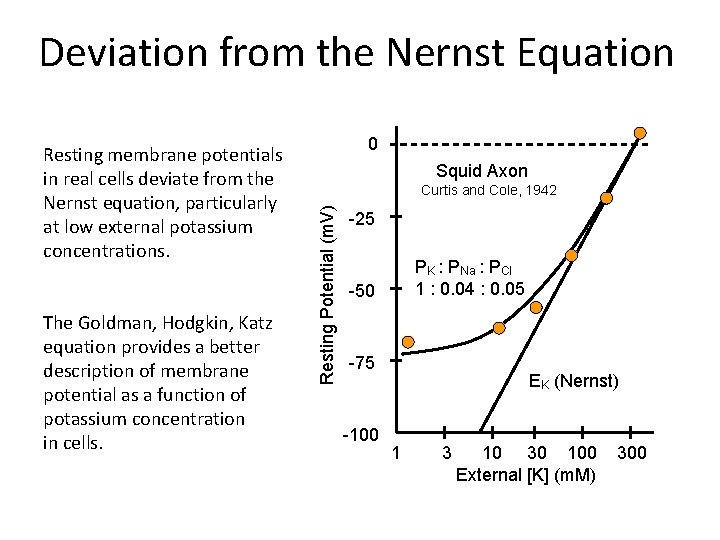
Deviation from the Nernst Equation The Goldman, Hodgkin, Katz equation provides a better description of membrane potential as a function of potassium concentration in cells. 0 Squid Axon Curtis and Cole, 1942 Resting Potential (m. V) Resting membrane potentials in real cells deviate from the Nernst equation, particularly at low external potassium concentrations. -25 PK : PNa : PCl 1 : 0. 04 : 0. 05 -50 -75 -100 EK (Nernst) 1 3 10 30 100 External [K] (m. M) 300

The Goldman Hodgkin Katz Equation • Resting Vm depends on the concentration gradients and on the relative permeabilities to Na, K and Cl. The Nernst Potential for an ion does not depend on membrane permeability to that ion. • The GHK equation describes a steady state condition, not electrochemical equilibrium. • There is net flux of individual ions, but no net charge movement. • The cell must supply energy to maintain its ionic gradients.

GHK Equation: Sample Calculation Suppose PK : PNa : PCl = 1 : 0. 1 : 1 = 60 m. V * log (18. 7 / 213) = 60 m. V * 1. 06 = 63 m. V

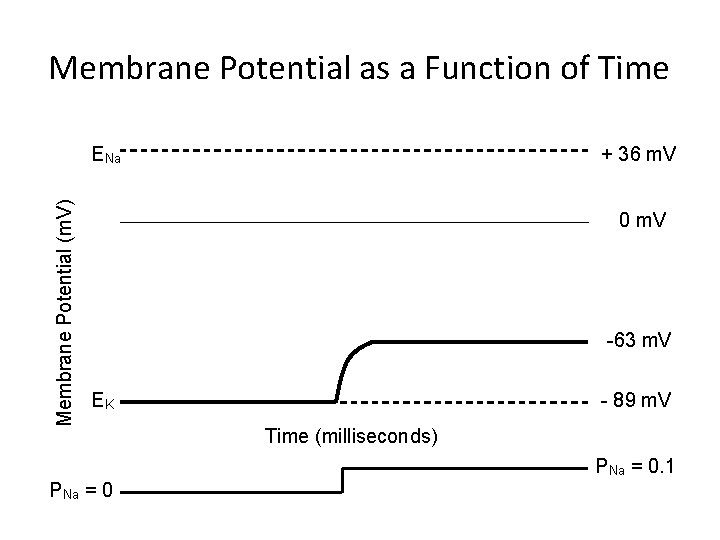
Membrane Potential as a Function of Time Membrane Potential (m. V) ENa + 36 m. V 0 m. V -63 m. V EK - 89 m. V Time (milliseconds) PNa = 0. 1 PNa = 0

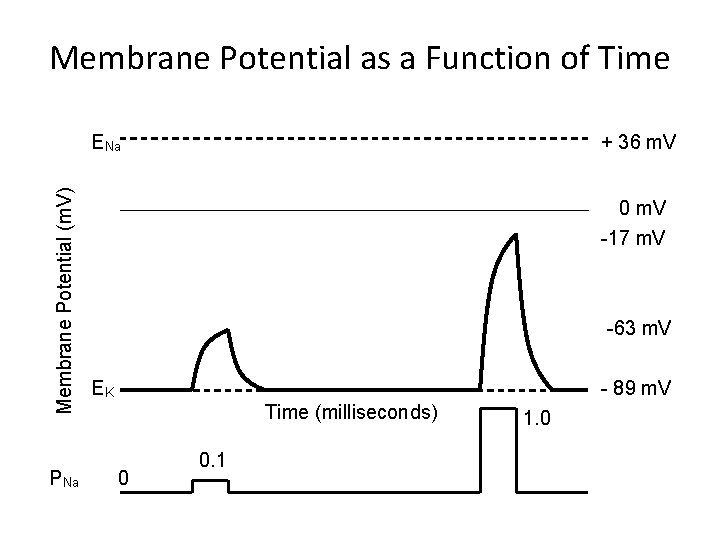
Membrane Potential as a Function of Time Membrane Potential (m. V) ENa PNa + 36 m. V 0 m. V -17 m. V -63 m. V EK - 89 m. V Time (milliseconds) 0 0. 1 1. 0

Summary: I. Cells are always at water equilibrium • Osmolarity inside = Osmolarity outside • The cell membrane is a barrier to polar, charged molecules Þ cells need specific transport mechanisms II. Ions crossing the membrane create a voltage difference • Few ions must cross to generate a significant potential Þ bulk neutrality of internal and external solution III. Permeable ions move toward electrochemical equilibrium • Eion = (60 m. V / z) * log ([Ion]out / [Ion]in) @ 30°C

Summary (continued): IV. The Goldman, Hodgkin, Katz equation gives the steady state membrane potential when Na, K and Cl are permeable • In this case, Vm does depend on the relative permeability to each ion and there is steady flux of Na and K Þ The cell must supply energy to maintain its ionic gradients

Additional Reading • Kay AR, Blaustein MP. (2019) Evolution of our understanding of cell volume regulation by the pump leak mechanism. J Gen Physiol. 151: 407 416. Erratum in: J Gen Physiol. (2019) 151: 606 607. • Armstrong CM. (2003) The Na/K pump, Cl ion, and osmotic stabilization of cells. Proc Natl Acad Sci U S A. 100: 6257 62. • Finkelstein A. (1976) Water and nonelectrolyte permeability of lipid bilayer membranes. J Gen Physiol. 68: 127 35.