MellinBarnes representation Converse Mapping theorem and Feynmans diagrams

Mellin-Barnes representation Converse Mapping theorem and Feynman's diagrams David Greynat Institut de Física Corpuscular 25 th October 2006 In collaboration with Samuel FRIOT and Eduardo de RAFAEL Phys. Letter B 628 (2005)

Mellin-Barnes representation Converse Mapping theorem and Feynman's diagrams – 25 th October 06 Different methods How to obtain an asymptotic expansion ? 1. Parameterisation of Feynman’s graphs ❏ Divergences on parameters in naïve ❏ Quickly impossible to calculate developments 2. Dimensional regularisation ❏ Abandon of Feynman’s parameters: all integrals converge ❏ Immediate calculation on momenta (integration by part) 3. Effective Theory ❏ Replacement of the total theory by ❏ Problems with the « matching » pertinent operators 4. Sub-Graphs strategy (Smirnov) ❏ Taylor’s Expansions in pertinent parameters ❏ Tedious calculations but we can use a computer 2

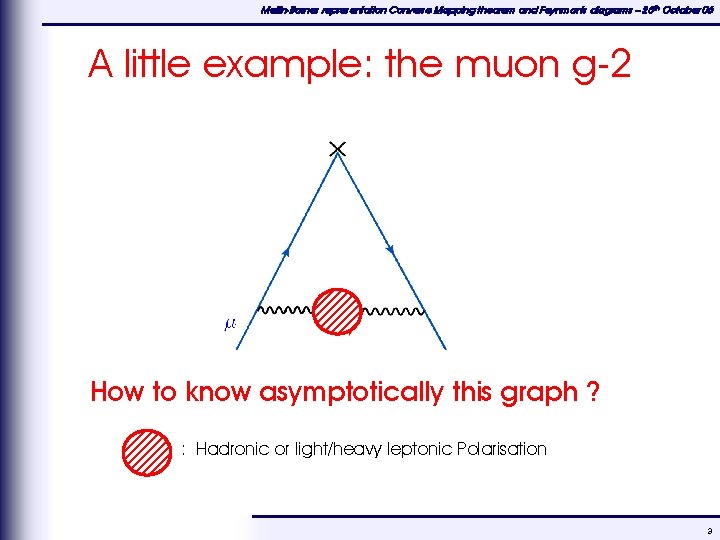
Mellin-Barnes representation Converse Mapping theorem and Feynman's diagrams – 25 th October 06 A little example: the muon g-2 How to know asymptotically this graph ? : Hadronic or light/heavy leptonic Polarisation 3

Mellin-Barnes representation Converse Mapping theorem and Feynman's diagrams – 25 th October 06 Feynman’s Parameterisation Dispersion relation 4

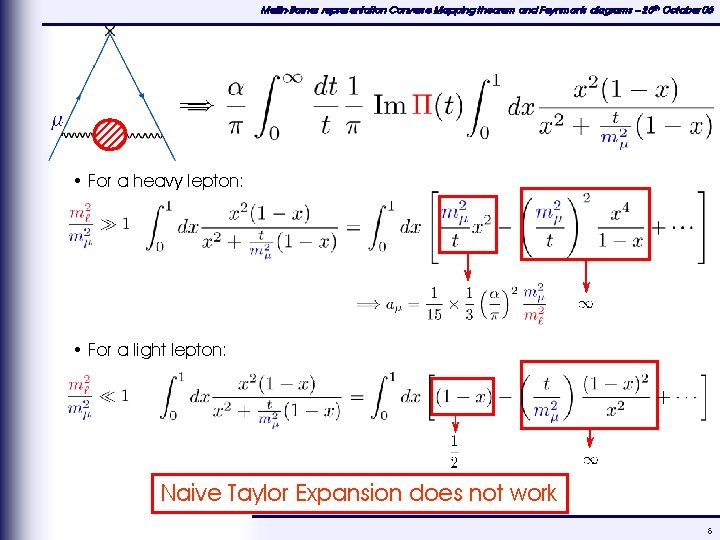
Mellin-Barnes representation Converse Mapping theorem and Feynman's diagrams – 25 th October 06 • For a heavy lepton: • For a light lepton: Naive Taylor Expansion does not work 5

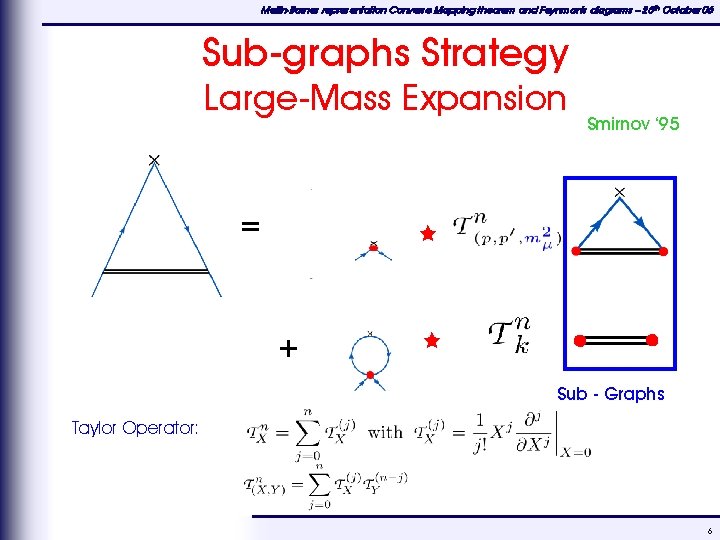
Mellin-Barnes representation Converse Mapping theorem and Feynman's diagrams – 25 th October 06 Sub-graphs Strategy Large-Mass Expansion = Smirnov ‘ 95 + Sub - Graphs Taylor Operator: 6

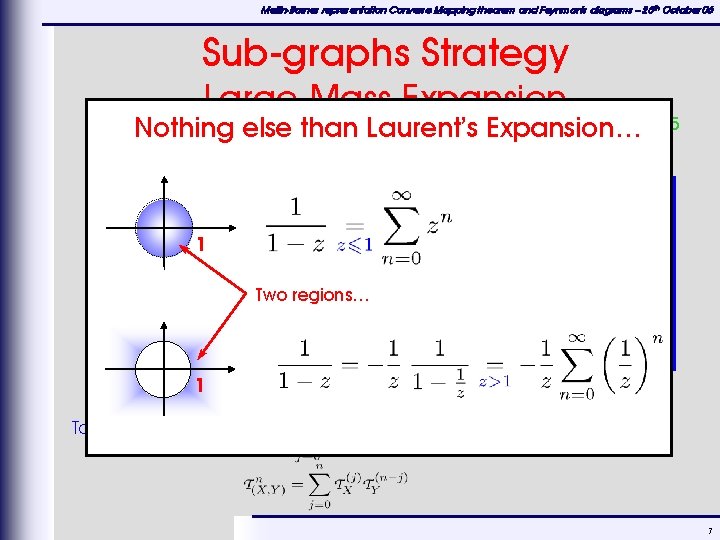
Mellin-Barnes representation Converse Mapping theorem and Feynman's diagrams – 25 th October 06 Sub-graphs Strategy Large-Mass Expansion Smirnov ‘ 95 Nothing else than Laurent’s Expansion… 1 = Two regions… + 1 Sub - Graphs Taylor Operator: 7

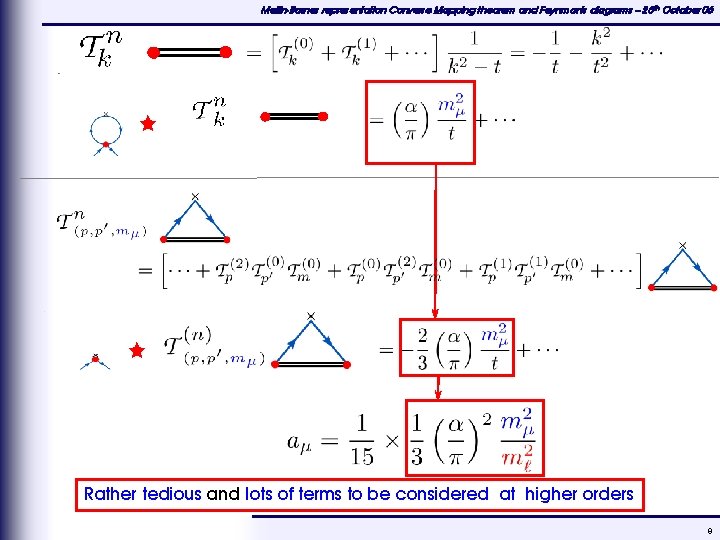
Mellin-Barnes representation Converse Mapping theorem and Feynman's diagrams – 25 th October 06 Rather tedious and lots of terms to be considered at higher orders 8

Mellin-Barnes representation Converse Mapping theorem and Feynman's diagrams – 25 th October 06 Mellin’s Transform ❏ Definitions If f is integrable and if: Then ❏ is analytic in and it is the fundamental strip Examples 9

Mellin-Barnes representation Converse Mapping theorem and Feynman's diagrams – 25 th October 06 Converse Mapping Theorem This theorem gives a link between the singularities of the Mellin’s Transform and the asymptotic expansion of the function ❏ Singular Element Laurent’s expansion of f in ss p: Singular Expansion ❏ Formal sum of all singular elements. ❏ Example 10

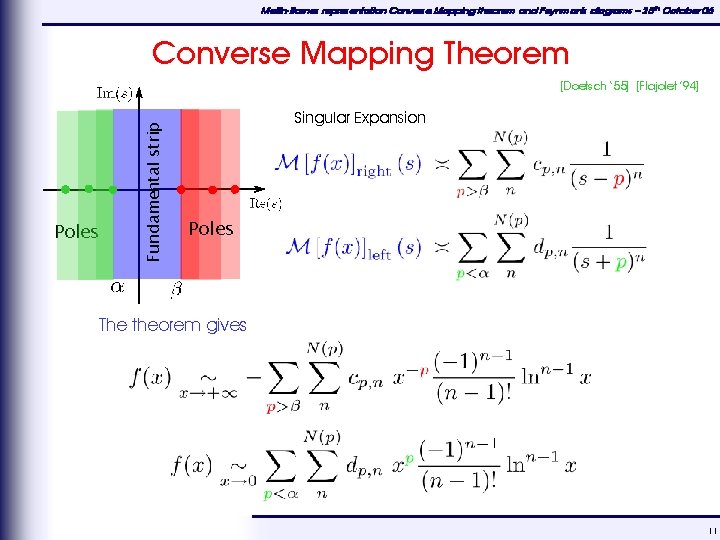
Mellin-Barnes representation Converse Mapping theorem and Feynman's diagrams – 25 th October 06 Converse Mapping Theorem Poles Fundamental strip [Doetsch ‘ 55] [Flajolet ’ 94] Singular Expansion Poles The theorem gives 11

Mellin-Barnes representation Converse Mapping theorem and Feynman's diagrams – 25 th October 06 Applications to QFT ❏ Feynman’s Representation ❏ Mellin-Barnes’ Representation & identification of the Fundamental Strip ❏ Converse Mapping Theorem 12

Mellin-Barnes representation Converse Mapping theorem and Feynman's diagrams – 25 th October 06 Coming back to our previous little example… Lautrup, de Rafael ‘ 69 13

Mellin-Barnes representation Converse Mapping theorem and Feynman's diagrams – 25 th October 06 : Singular Expansion on the right of the fundamental strip : Singular Expansion on the left of the fundamental strip 14

Mellin-Barnes representation Converse Mapping theorem and Feynman's diagrams – 25 th October 06 Exact expansion : Singular Expansion on the right of the fundamental strip : Singular Expansion on the left of the fundamental strip 15

Mellin-Barnes representation Converse Mapping theorem and Feynman's diagrams – 25 th October 06 Some other examples… 16

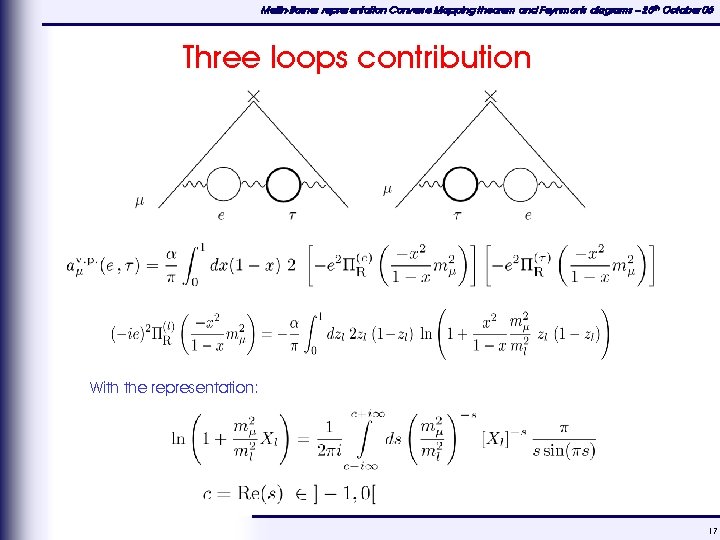
Mellin-Barnes representation Converse Mapping theorem and Feynman's diagrams – 25 th October 06 Three loops contribution With the representation: 17

Mellin-Barnes representation Converse Mapping theorem and Feynman's diagrams – 25 th October 06 Results 18

Mellin-Barnes representation Converse Mapping theorem and Feynman's diagrams – 25 th October 06 19

Mellin-Barnes representation Converse Mapping theorem and Feynman's diagrams – 25 th October 06 20

Mellin-Barnes representation Converse Mapping theorem and Feynman's diagrams – 25 th October 06 Asymptotic results We easily check and extend Czarnecki and Skrzypek ’ 99 21

Mellin-Barnes representation Converse Mapping theorem and Feynman's diagrams – 25 th October 06 Masters Integrals 22

Mellin-Barnes representation Converse Mapping theorem and Feynman's diagrams – 25 th October 06 Applications to Large NC QCD Eduardo de Rafael, work in progress 23

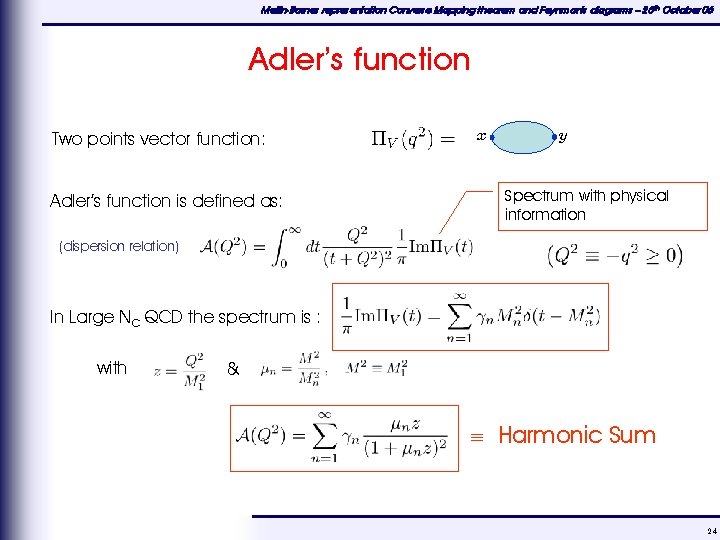
Mellin-Barnes representation Converse Mapping theorem and Feynman's diagrams – 25 th October 06 Adler’s function Two points vector function: Adler’s function is defined as: x y Spectrum with physical information (dispersion relation) In Large NC QCD the spectrum is : with & Harmonic Sum 24

Mellin-Barnes representation Converse Mapping theorem and Feynman's diagrams – 25 th October 06 Two-Point Functions are Harmonic Sums in Large-Nc QCD where and Harmonic Sums are defined by a Base Function and a Dirichlet’s Series Base Function: Dirichlet’s Series: e. g. Riemann zeta-function: How does the Dirichlet’s Series appear ? ? 25

Mellin-Barnes representation Converse Mapping theorem and Feynman's diagrams – 25 th October 06 Harmonic Sums have a factorizable Mellin-Transform Base Function: Dirichlet’s Series: Comment on the factorization of the Comment on the fundamental strip ( Recall that dependence ) 26

Mellin-Barnes representation Converse Mapping theorem and Feynman's diagrams – 25 th October 06 Conclusions ❏ Very efficient method comparing with others (Strategy of regions, sub-graphs, …) ❏ Mellin-Barnes representation is the pertinent tool for expansions in heavy and light scales. ❏ Interesting for Large NC - Harmonic Sums are the natural framework for Large-Nc QCD - QCD Generalized Two-Point Function & Dirichlet’s Series 27