MEHANIKA II KINEMATIKA TIJELA UVOD KRUTO TIJELO tijelo

MEHANIKA II KINEMATIKA TIJELA UVOD KRUTO TIJELO – tijelo sastavljeno od beskonačnog broja točaka, čija se udaljenost ne mijenja. Zakon gibanja poznat – ako je poznata brzina jedne točke te kutna brzina i/ili kutno ubrzanje. Položaj tijela poznat – ako su poznate koordinate najmanje tri točke koje ne leže na istom pravcu. Osnovna gibanja krutog tijela: -translacija, -rotacija oko nepomične osi (točke), -opće gibanje u ravnini, -opće gibanje u prostoru.

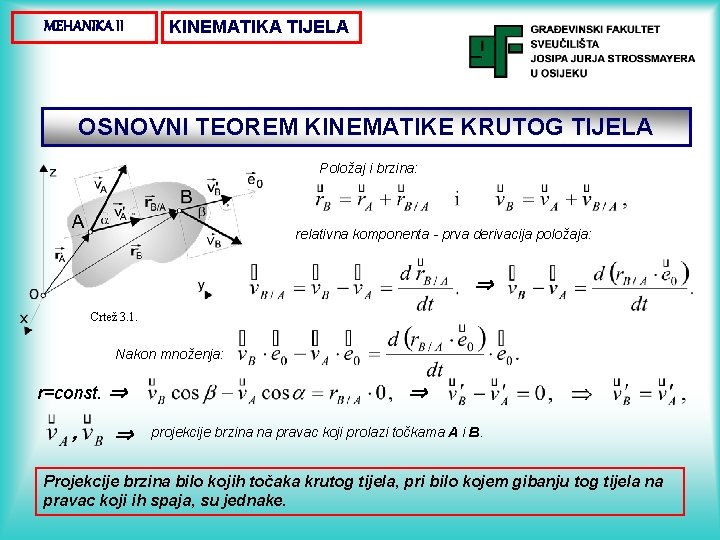
MEHANIKA II KINEMATIKA TIJELA OSNOVNI TEOREM KINEMATIKE KRUTOG TIJELA Položaj i brzina: relativna komponenta - prva derivacija položaja: Crtež 3. 1. Nakon množenja: r=const. , projekcije brzina na pravac koji prolazi točkama A i B. Projekcije brzina bilo kojih točaka krutog tijela, pri bilo kojem gibanju tog tijela na pravac koji ih spaja, su jednake.

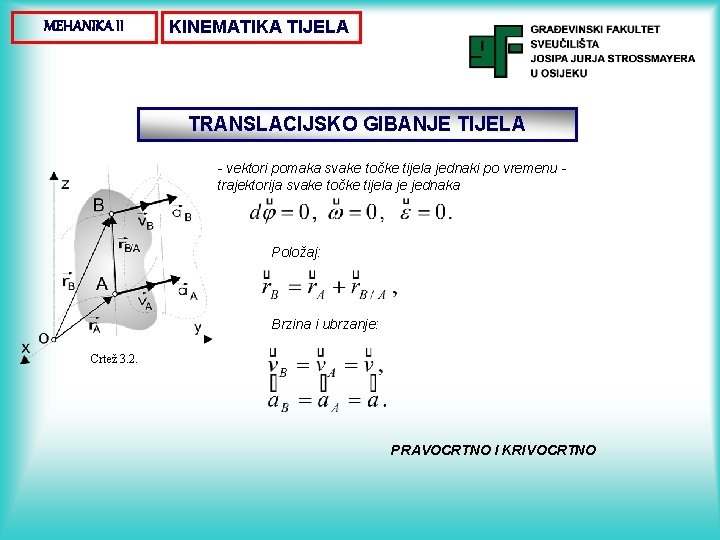
MEHANIKA II KINEMATIKA TIJELA TRANSLACIJSKO GIBANJE TIJELA - vektori pomaka svake točke tijela jednaki po vremenu trajektorija svake točke tijela je jednaka Položaj: Brzina i ubrzanje: Crtež 3. 2. PRAVOCRTNO I KRIVOCRTNO

MEHANIKA II KINEMATIKA TIJELA ROTACIJSKO GIBANJE TIJELA OKO NEPOMIČNE OSI - dvije nepomične točke TIJELA koje leže na istom pravcu sve točke tog tijela koje leže na tom pravcu su nepomične - kutna brzina: - brzina: - kutno ubrzanje: Crtež 3. 3. - ubrzanje: - komponente ubrzanja:

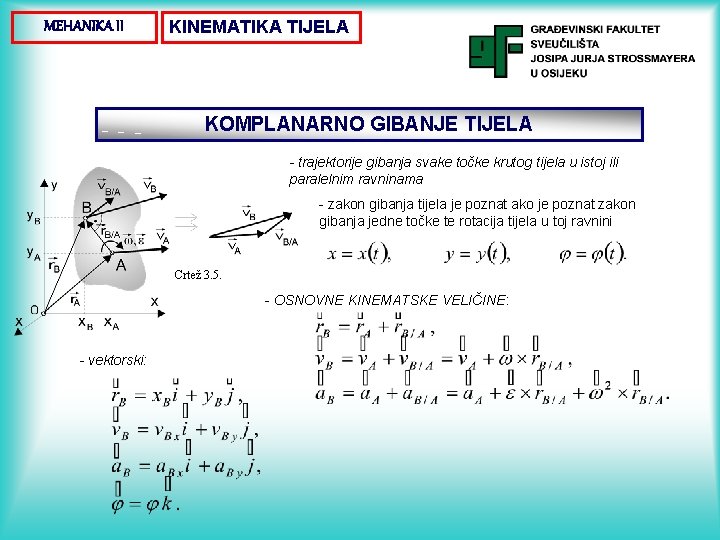
MEHANIKA II KINEMATIKA TIJELA KOMPLANARNO GIBANJE TIJELA - trajektorije gibanja svake točke krutog tijela u istoj ili paralelnim ravninama - zakon gibanja tijela je poznat ako je poznat zakon gibanja jedne točke te rotacija tijela u toj ravnini Crtež 3. 5. - OSNOVNE KINEMATSKE VELIČINE: - vektorski:

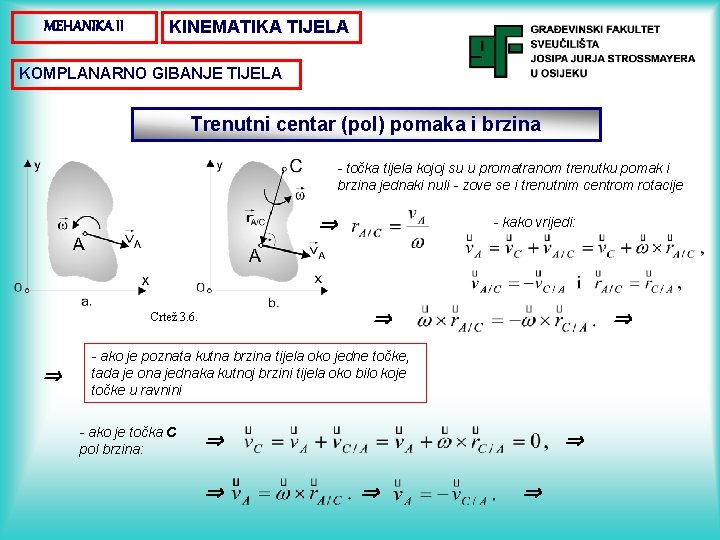
MEHANIKA II KINEMATIKA TIJELA KOMPLANARNO GIBANJE TIJELA Trenutni centar (pol) pomaka i brzina - točka tijela kojoj su u promatranom trenutku pomak i brzina jednaki nuli - zove se i trenutnim centrom rotacije Crtež 3. 6. - kako vrijedi: - ako je poznata kutna brzina tijela oko jedne točke, tada je ona jednaka kutnoj brzini tijela oko bilo koje točke u ravnini - ako je točka C pol brzina:

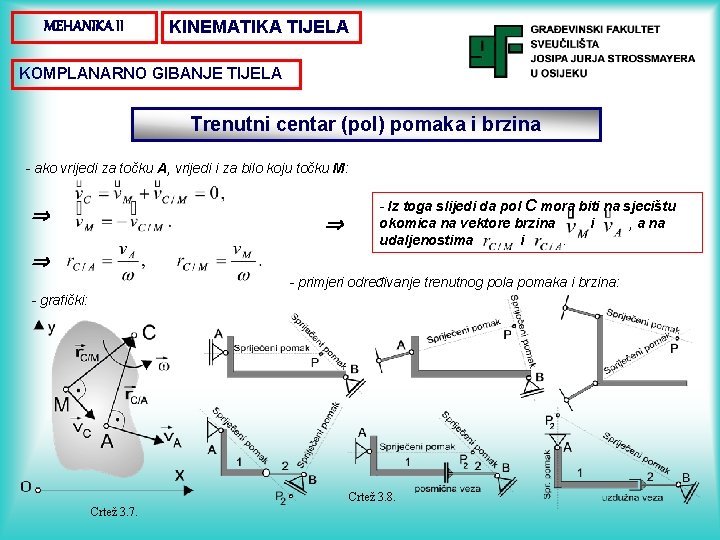
MEHANIKA II KINEMATIKA TIJELA KOMPLANARNO GIBANJE TIJELA Trenutni centar (pol) pomaka i brzina - ako vrijedi za točku A, vrijedi i za bilo koju točku M: - Iz toga slijedi da pol C mora biti na sjecištu okomica na vektore brzina i , a na udaljenostima i. - primjeri određivanje trenutnog pola pomaka i brzina: - grafički: Crtež 3. 8. Crtež 3. 7.

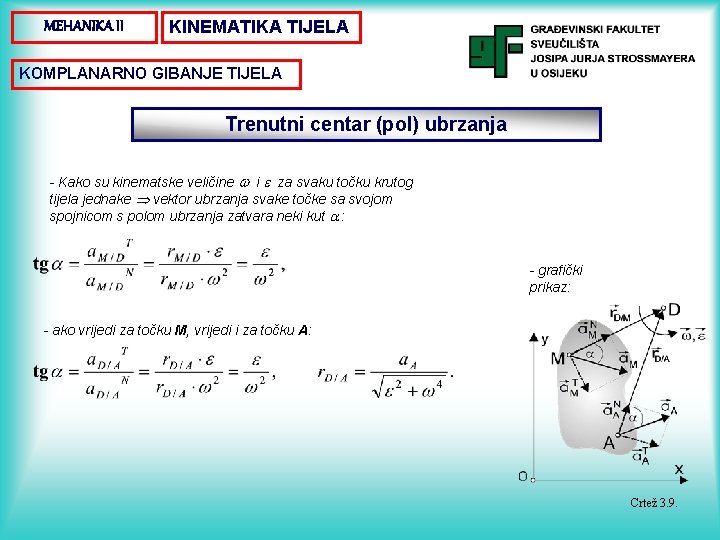
MEHANIKA II KINEMATIKA TIJELA KOMPLANARNO GIBANJE TIJELA Trenutni centar (pol) ubrzanja - točka tijela kojoj je u promatranom trenutku ubrzanje jednako nuli - ako je točka D pol ubrzanja: - ako vrijedi za točku A, vrijedi i za bilo koju točku M: - pomoću jediničnih vektora tangente i normale: - po iznosu:

MEHANIKA II KINEMATIKA TIJELA KOMPLANARNO GIBANJE TIJELA Trenutni centar (pol) ubrzanja - Kako su kinematske veličine i za svaku točku krutog tijela jednake vektor ubrzanja svake točke sa svojom spojnicom s polom ubrzanja zatvara neki kut : - grafički prikaz: - ako vrijedi za točku M, vrijedi i za točku A: Crtež 3. 9.

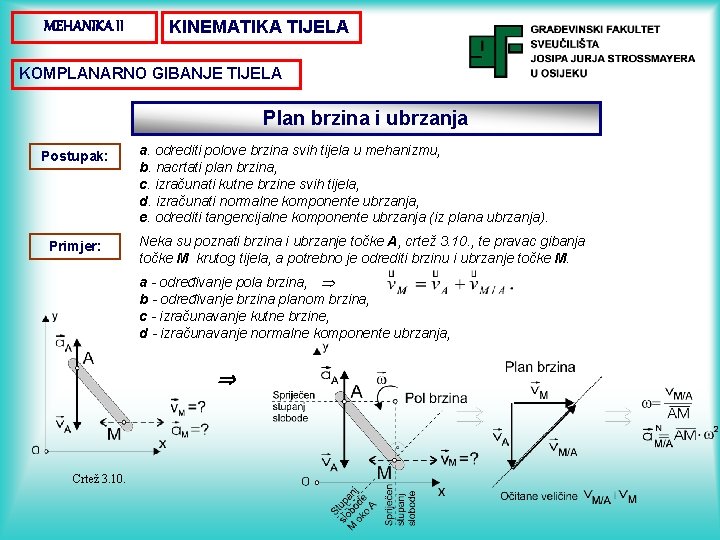
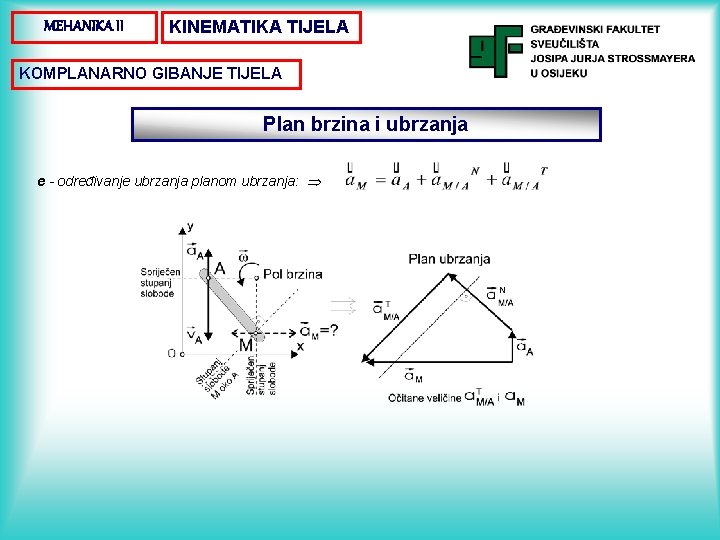
MEHANIKA II KINEMATIKA TIJELA KOMPLANARNO GIBANJE TIJELA Plan brzina i ubrzanja Postupak: Primjer: a. odrediti polove brzina svih tijela u mehanizmu, b. nacrtati plan brzina, c. izračunati kutne brzine svih tijela, d. izračunati normalne komponente ubrzanja, e. odrediti tangencijalne komponente ubrzanja (iz plana ubrzanja). Neka su poznati brzina i ubrzanje točke A, crtež 3. 10. , te pravac gibanja točke M krutog tijela, a potrebno je odrediti brzinu i ubrzanje točke M. a - određivanje pola brzina, b - određivanje brzina planom brzina, c - izračunavanje kutne brzine, d - izračunavanje normalne komponente ubrzanja, Crtež 3. 10.

MEHANIKA II KINEMATIKA TIJELA KOMPLANARNO GIBANJE TIJELA Plan brzina i ubrzanja e - određivanje ubrzanja planom ubrzanja:

MEHANIKA II KINEMATIKA TIJELA KOMPLANARNO GIBANJE TIJELA Složeno gibanje tijela – kinematski član, par i lanac Složeno gibanje krutog tijela definira se kao složeno gibanje točke, odnosno, kao gibanje tijela iz odnosa apsolutnog, relativnog i prijenosnog gibanja dviju točak - zavisno : Crtež 3. 13. Kada se u kinematici tijela govori o složenom gibanju, u pravilu se misli na složeno gibanje dva ili tri međusobno povezana kruta tijela. Ako su dva tijela koja se gibaju vezana, bilo zglobnom, posmičnom ili uzdužnom vezom, dakle vezom koja dozvoljava isključivo jedan stupanj slobode, oni predstavljaju kinematski par, a svako tijelo naziva se kinematski član. Tri ili više kinematskih članova jednako vezanih, nazivaju se kinematski lanac ili niz. Takvi sustavi nazivaju se mehanizmi. Složeno gibanje dva ili tri vezana kruta tijela definira se na sljedeći način: - a) definira se kinematika jednog tijela iz uvjeta veza pa je gibanje tijela poznato ako je poznato gibanje jedne točke tog tijela i rotacija tog tijela b) definira se gibanje zajedničke tog tijela c) definira se kinematika drugog tijela pa je gibanje drugog tijela poznato ako je poznato gibanje zajedničke točke oba tijela i rotacija tog tijela d) kinematskim vezama mogu se odrediti kinematske veličine bilo koje točke jednog

MEHANIKA II KINEMATIKA TIJELA KOMPLANARNO GIBANJE TIJELA Teorem triju polova – Kennedyjev teorem Ako se promatra komplanarno gibanje tijela, odnosno komplanarno gibanje mehanizama, trenutni centar brzina može biti: - apsolutni, odnosno centar koji ima apsolutnu brzinu u odnosu na nepomični koordinatni sustav jednaku nuli i relativni, odnosno centar koji ima relativnu brzinu u odnosu na pomični koordinatni sustav ili u odnosu na drugo tijelo jednaku nuli. - točka M - promatrana točka: Crtež 3. 15. - kinematski uvjet za trenutni pol P 1, 2 - da mu je apsolutna brzina jednaka, bez obzira u odnosu na koje se tijelo promatra njegovo gibanje: vektori položaja jednaki: - udaljenosti apsolutnih polova od relativnog, ovisno o veličinama i smjerovima kutnih brzina :

MEHANIKA II KINEMATIKA TIJELA KOMPLANARNO GIBANJE TIJELA Teorem triju polova – Kennedyjev teorem Iz toga slijedi zaključak da je relativni pol uvijek na istom pravcu na kojemu su apsolutni i prijenosni. Ovaj prikaz dokazuje Kennedyjev teorem triju polova koji glasi: U komplanarnom gibanju kinematskog para (dva kruta tijela), za svaki kinematski član u svakom trenutku gibanja, prijenosni, relativni i apsolutni pol moraju ležati na istom pravcu. Teorem vrijedi isključivo ako su apsolutna i prijenosna rotacija suprotnog smjera, a najlakše ga je primijeniti kod zglobne veze između dva tijela. Kada su dva tijela povezana na drugi način, najčešće posmičnom, uzdužnom ili nekom drugom vezom, mogu se pojaviti još dva specijalna slučaja:

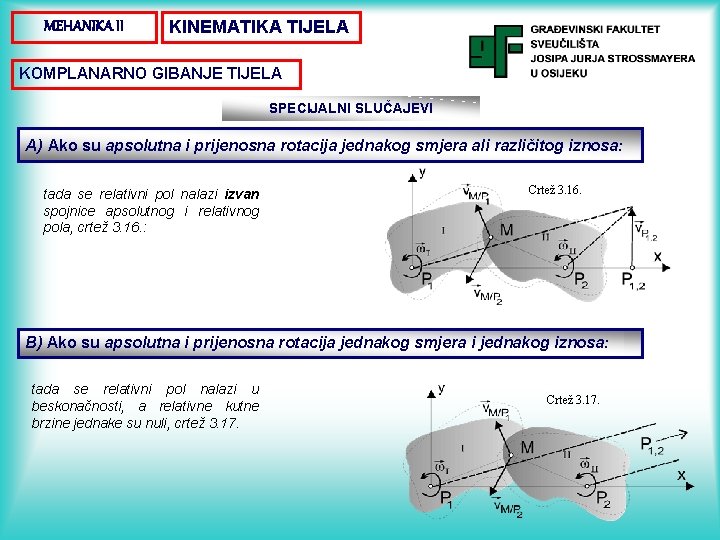
MEHANIKA II KINEMATIKA TIJELA KOMPLANARNO GIBANJE TIJELA SPECIJALNI SLUČAJEVI A) Ako su apsolutna i prijenosna rotacija jednakog smjera ali različitog iznosa: tada se relativni pol nalazi izvan spojnice apsolutnog i relativnog pola, crtež 3. 16. : Crtež 3. 16. B) Ako su apsolutna i prijenosna rotacija jednakog smjera i jednakog iznosa: tada se relativni pol nalazi u beskonačnosti, a relativne kutne brzine jednake su nuli, crtež 3. 17. Crtež 3. 17.

MEHANIKA II KINEMATIKA TIJELA KOMPLANARNO GIBANJE TIJELA Kinematski lanac Uz iste pretpostavke te iste kinematske uvjete tijela I u odnosu na tijelo II i tijela III u odnosu na tijelo II, vrijede glavne karakteristike za relativne polove P 1, 2 i P 2, 3, crtež 3. 18 Crtež 3. 18.

MEHANIKA II KINEMATIKA TIJELA KOMPLANARNO GIBANJE TIJELA Primjeri određivanja relativnih polova Crtež 3. 19.

MEHANIKA II KINEMATIKA TIJELA KOMPLANARNO GIBANJE TIJELA Plan horizontalnih i vertikalnih pomaka Načelo virtualnog rada je u statici jasno definirano osnovnim stavkom koji glasi: Sustav dva ili više tijela s vezama i osloncima je u ravnoteži ako je virtualni rad svih promatranih aktivnih sila na bilo kojim virtualnim pomacima koji zadovoljavaju uvjete veza (rubnih uvjeta) jednak nuli. Uz pomoć stavka virtualnog rada i poznavanja pomaka sustava koji se giba u ravnini s jednim stupnjem slobode, lako se određuju sile u vezama i osloncima te unutarnje sile u presjecima nosača. Osnovno je pravilo u sljedećem: ukloniti vanjsku ili dodati unutarnju vezu kako bi se definirao virtualni (zamišljeni) rad tražene sile u vezama ili unutarnje sile - “ono što tražimo to oslobađamo”. Preostaje definirati plan pomaka cijelog sustava na temelju preostalih uvjeta veza i oslonaca te definirati virtualne radove svih promatranih aktivnih sila. Na crtežu 3. 23. prikazani su jednostavni primjeri određivanja sila u osloncima ili unutarnjih sila u presjecima. Crtež 3. 23.

MEHANIKA II KINEMATIKA TIJELA KOMPLANARNO GIBANJE TIJELA Plan horizontalnih i vertikalnih pomaka Po sličnom načelu dolazi se i do kinematskih veličina koje su u ovom slučaju stvarne. U pravilu je za zadani mehanizam s jednim stupnjem slobode, na temelju kinematske veličine jednog tijela (pomak, brzina ili ubrzanje), potrebno odrediti kinematske veličine drugog. POSTUPAK 1). određuju se polovi pomaka i brzina prema uvjetima veza i oslonaca ZA SVAKO TIJELO, 2). crta se poznata kinematska veličina jednog tijela, 3). konstruira se plan pomaka preostalog dijela mehanizma, prema uvjetima veza i oslonaca, 4). iz geometrijskih uvjeta određuju se kinematske veličine preostalih tijela kao i tijela za koje se iste traže, 5). prema dobivenim veličinama mogu se odrediti kinematske veličine bilo koje točke mehanizma. Crtež 3. 23.

MEHANIKA II KINEMATIKA TIJELA KOMPLANARNO GIBANJE TIJELA Plan horizontalnih i vertikalnih pomaka PRIMJER Neka je za zadani konstrukcijski sustav s jednim stupnjem slobode (mehanizam), za poznate kinematske veličine tijela 1, potrebno odrediti kinematske veličine tijela 2, crtež 3. 24. Crtež 3. 24.