MEHANIKA I STATIKA MEH 1 16 17 P

MEHANIKA I (STATIKA) MEH 1 16. 17 P 4 24. 10. 2020. 1

PROIZVOLJAN RAVANSKI SISTEM SILA �Teorem o redukciji sile na tačku (o paralelnom prenošenju sile) ◦ Silu koja deluje na kruto telo, bez promene njenog dejstva, moguće je translacijom redukovati (paralelno preneti) na bilo koju drugu tačku, ako joj pridružimo moment sprega jednak njenom momentu za tu tačku. 24. 10. 2020. 2

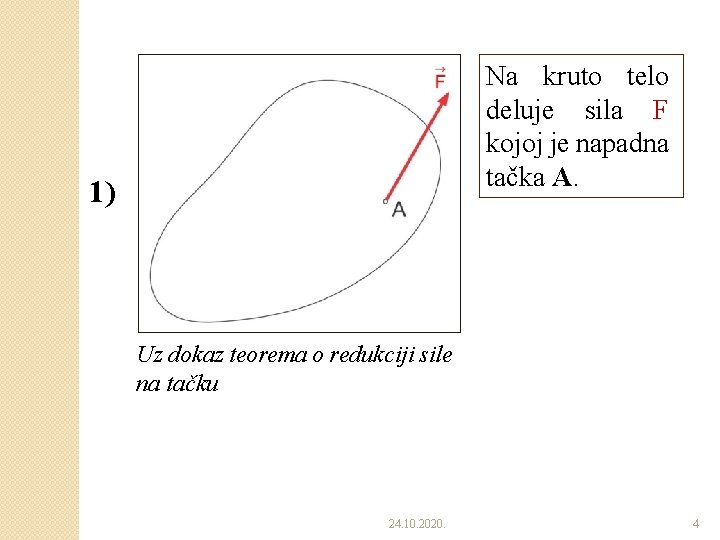
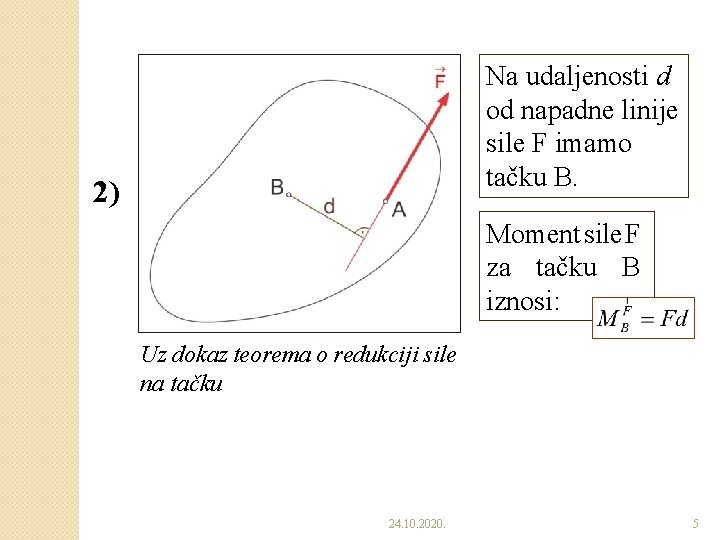
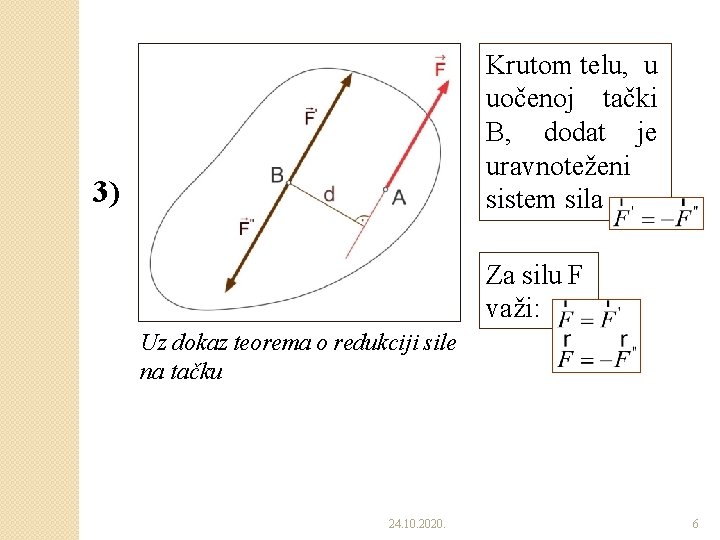
�Dokaz ◦ Neka na izvesno kruto telo deluje sila F kojoj je napadna tačka A. ◦ Na udaljenosti d od napadne linije date sile uočimo proizvoljnu tačku B. ◦ U uočenu tačku B dodajmo uravnoteženi sistem od dve sile. ◦ Dejstvo sile F se prema Aksiomu 2, dodavanjem uravnoteženog sistema od dve sile, neće promeniti. 24. 10. 2020. 3

Na kruto telo deluje sila F kojoj je napadna tačka A. 1) Uz dokaz teorema o redukciji sile na tačku 24. 10. 2020. 4

Na udaljenosti d od napadne linije sile F imamo tačku B. 2) Moment sile F za tačku B iznosi: Uz dokaz teorema o redukciji sile na tačku 24. 10. 2020. 5

Krutom telu, u uočenoj tački B, dodat je uravnoteženi sistem sila 3) Za silu F važi: Uz dokaz teorema o redukciji sile na tačku 24. 10. 2020. 6

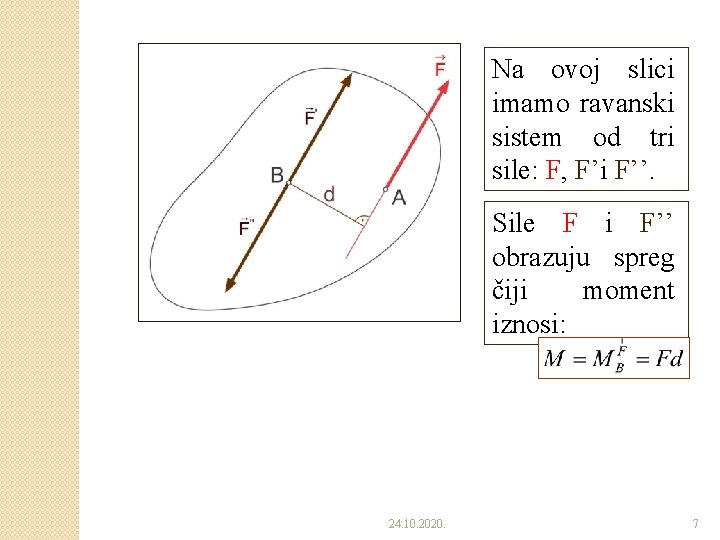
Na ovoj slici imamo ravanski sistem od tri sile: F, F’i F’’. Sile F i F’’ obrazuju spreg čiji moment iznosi: 24. 10. 2020. 7

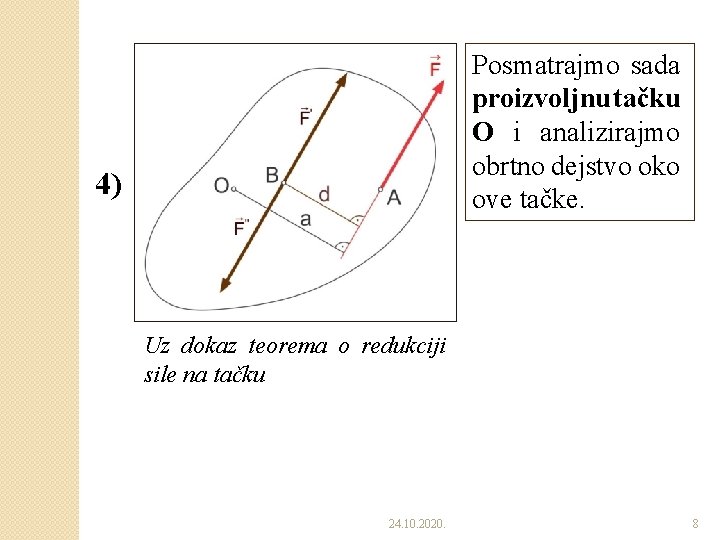
Posmatrajmo sada proizvoljnu tačku O i analizirajmo obrtno dejstvo oko ove tačke. 4) Uz dokaz teorema o redukciji sile na tačku 24. 10. 2020. 8

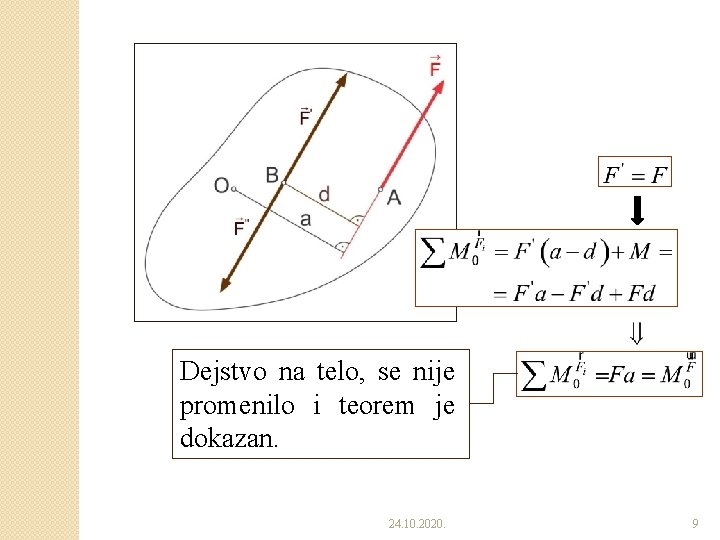
Dejstvo na telo, se nije promenilo i teorem je dokazan. 24. 10. 2020. 9

Moment sprega kao vektor pripada klasi slobodnih vektora i može se premeštati u bilo koju tačku, pa i u posmatranu tačku B (naš slučaj). 24. 10. 2020. 10

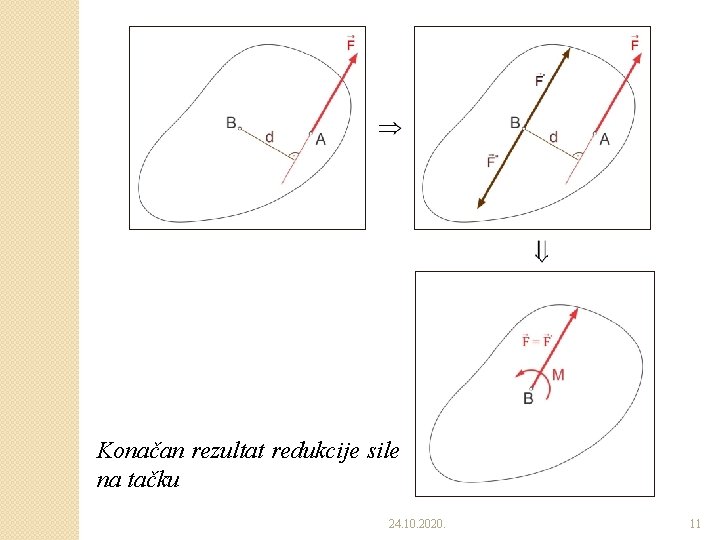
Konačan rezultat redukcije sile na tačku 24. 10. 2020. 11

�Redukcija (paralelno prenošenje) ravanskog sistema sila na datu tačku �Neka na kruto telo deluje proizvoljan ravanski sistem od n sila. �U ravni navedenog sistema sila uočimo proizvoljnu tačku O. �Korišćenjem prethodnog teorema, sve sile se mogu redukovati (paralelno preneti) na proizvoljnu tačku O, uz pridodavanje njihovih momenata za tu tačku. 24. 10. 2020. 12

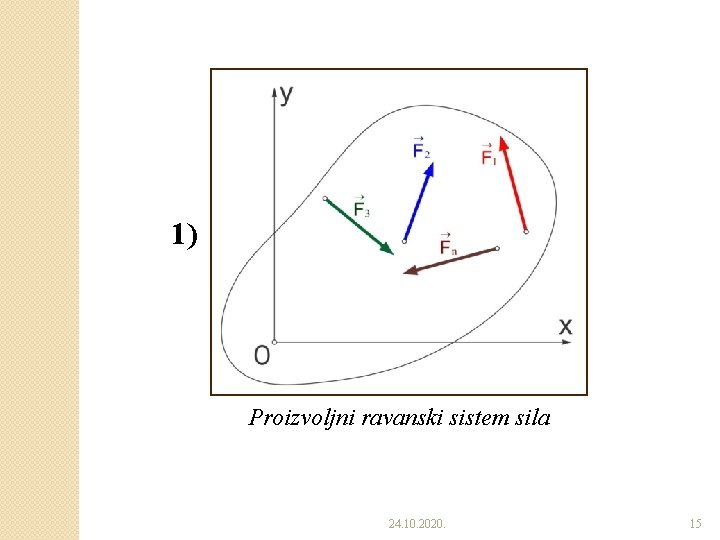
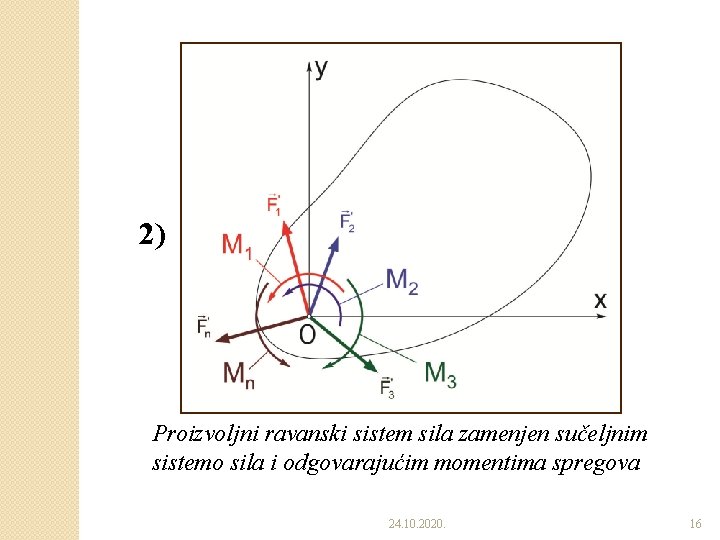
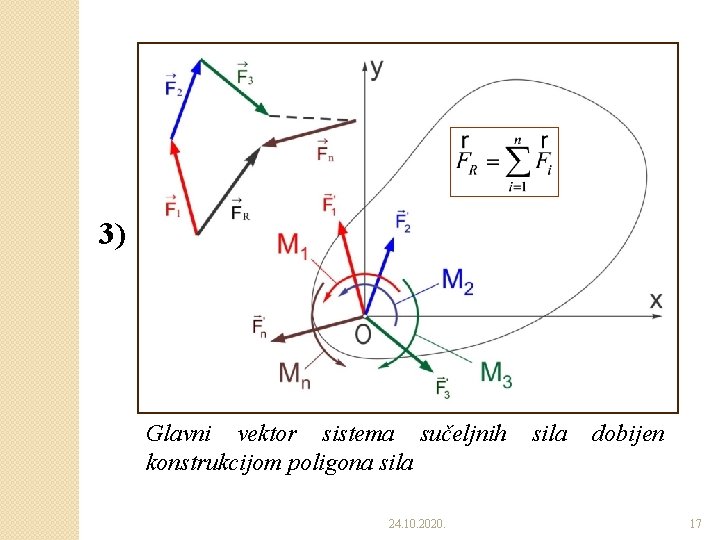
�Posle ove operacije na telo bi delovali ◦ Ravanski sistem sučeljnih sila i ◦ Ravanski sistem spregova. �Konstrukcijom poligona sila, može se doći do jedne sile koja zamenjuje sistem sučeljnih sila, a koja iznosi: Ovu silu zovemo glavni vektor proizvoljnog ravanskog sistema sila. 24. 10. 2020. 13

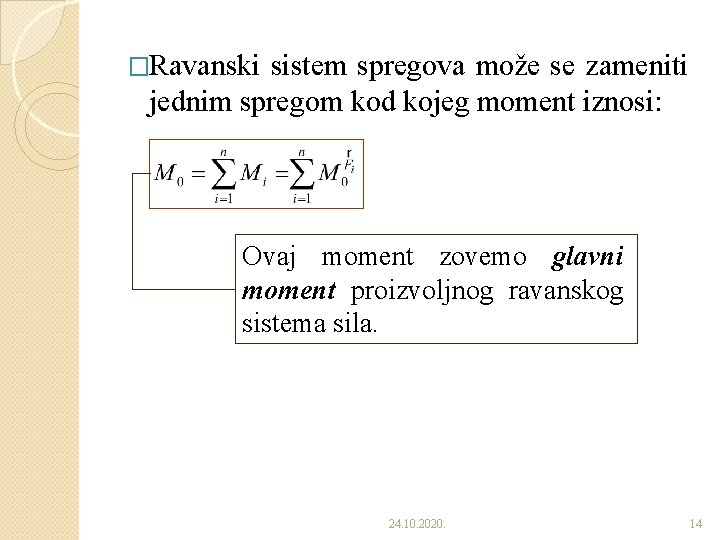
�Ravanski sistem spregova može se zameniti jednim spregom kod kojeg moment iznosi: Ovaj moment zovemo glavni moment proizvoljnog ravanskog sistema sila. 24. 10. 2020. 14

1) Proizvoljni ravanski sistem sila 24. 10. 2020. 15

2) Proizvoljni ravanski sistem sila zamenjen sučeljnim sistemo sila i odgovarajućim momentima spregova 24. 10. 2020. 16

3) Glavni vektor sistema sučeljnih konstrukcijom poligona sila 24. 10. 2020. sila dobijen 17

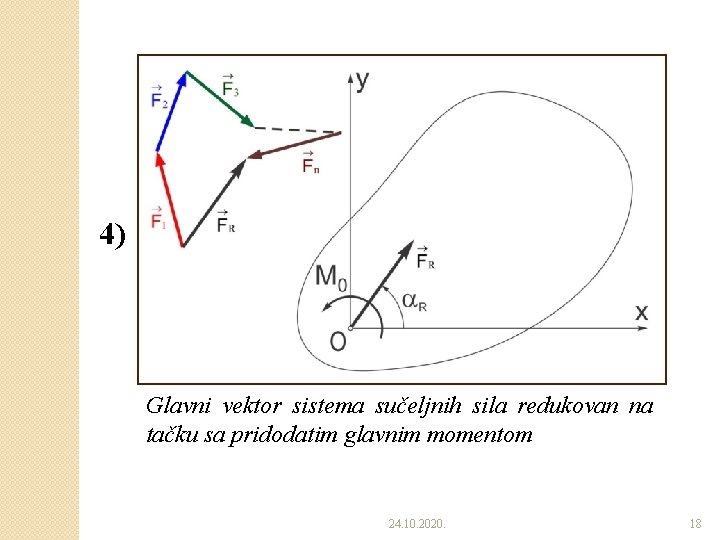
4) Glavni vektor sistema sučeljnih sila redukovan na tačku sa pridodatim glavnim momentom 24. 10. 2020. 18

�Glavni vektor: ◦ Može se redukovati na već posmatranu tačku O uz pridodavanje glavnog momenta. ◦ Ne predstavlja rezultantu jer proizvoljni ravanski sistem može zameniti ako mu se pridoda glavni moment. �ZAKLJUČAK: Svaki proizvoljni ravanski sistem sila koji deluje na kruto telo, može se zameniti glavnim vektorom sa napadnom tačkom O i jednim spregom kojem je moment jednak glavnom momentu datih sila za istu tačku. 24. 10. 2020. 19

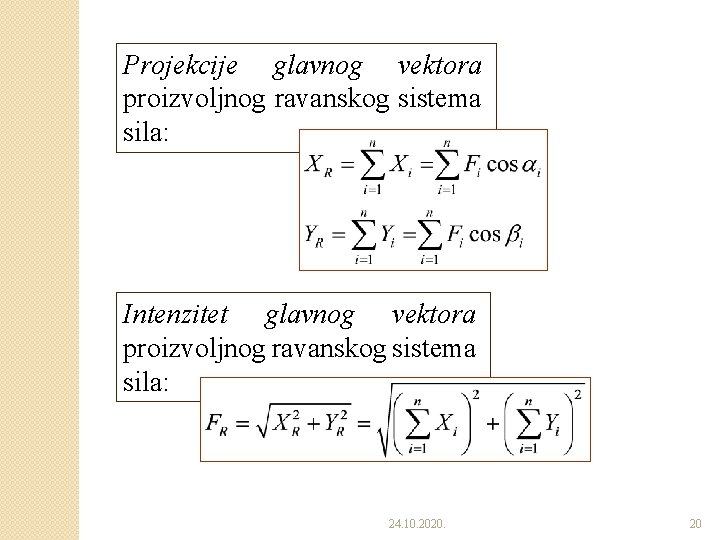
Projekcije glavnog vektora proizvoljnog ravanskog sistema sila: Intenzitet glavnog vektora proizvoljnog ravanskog sistema sila: 24. 10. 2020. 20

Pravac glavnog vektora proizvoljnog ravanskog sistema sila određujemo pomoću izraza: Intenzitet glavnog momenta proizvoljnog ravanskog sistema sila: 24. 10. 2020. 21

�Redukcija ravanskog sistema sila na prostiji oblik �Rezultat redukcije proizvoljnog ravanskog sistema sila je glavni vektor i glavni moment. �Analizirajmo nekoliko slučajeva. 24. 10. 2020. 22

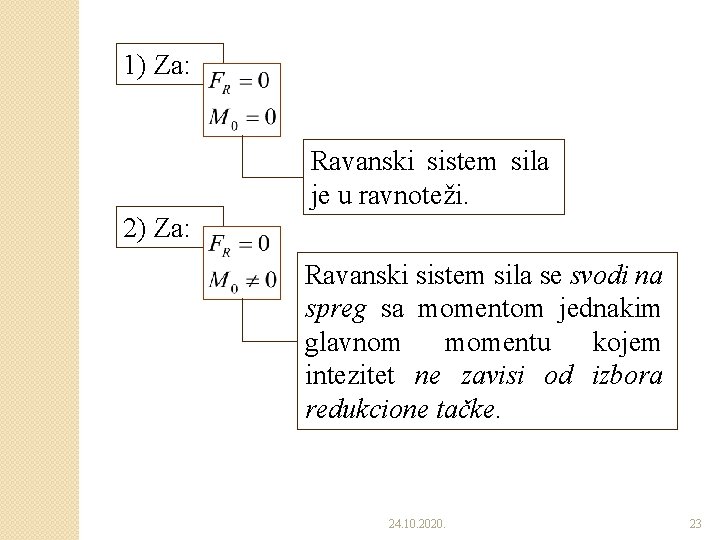
1) Za: Ravanski sistem sila je u ravnoteži. 2) Za: Ravanski sistem sila se svodi na spreg sa momentom jednakim glavnom momentu kojem intezitet ne zavisi od izbora redukcione tačke. 24. 10. 2020. 23

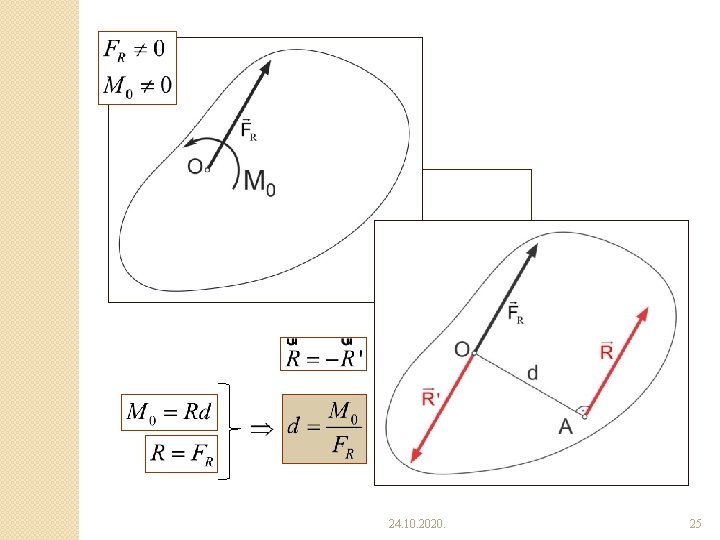
3) Za: 4) Za: Ravanski sistem sila se svodi na rezultantu kojoj napadna linija prolazi kroz redukcionu tačku. Ravanski sistem sila se svodi na rezultantu koja ne prolazi kroz redukcionu tačku O, već prolazi kroz neku drugu tačku. 24. 10. 2020. 24

24. 10. 2020. 25

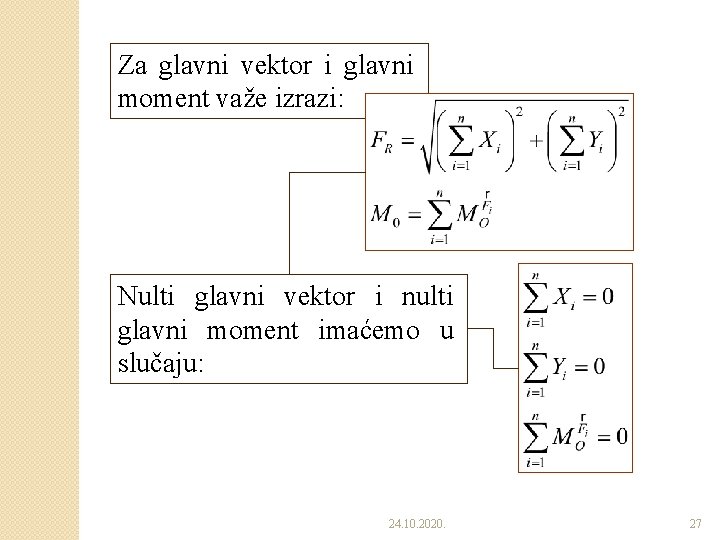
�Uslovi ravnoteže proizvoljnog ravanskog sistema sila ◦ Proizvoljni ravanski sistem sila je u ravnoteži ako su mu glavni vektor i glavni moment jednaki nuli (0). 24. 10. 2020. 26

Za glavni vektor i glavni moment važe izrazi: Nulti glavni vektor i nulti glavni moment imaćemo u slučaju: 24. 10. 2020. 27

◦ Prvi (osnovni) oblik uslova ravnoteže proizvoljnog ravanskog sistema sila: Za ravnotežu proizvoljnog ravanskog sistema sila, potrebno je i dovoljno, da mu sume projekcija sila na ose x i y, budu jednake nuli i da mu suma momenata svih sila, za bilo koju tačku u ravni dejstva, bude jednaka nuli. 24. 10. 2020. 28

◦ Drugi oblik uslova ravnoteže proizvoljnog ravanskog sistema sila: Za ravnotežu proizvoljnog ravanskog sistema sila, potrebno je i dovoljno, da mu sume momenata svih sila, za proizvoljne tačke A i B u ravni dejstva, budi jednake nuli, i da mu suma projekcija svih sila na osu x, koja nije normalna na pravu AB, bude jednaka nuli. 24. 10. 2020. 29

◦ Treći oblik uslova ravnoteže proizvoljnog ravanskog sistema sila (tri momentne jednačine): Za ravnotežu proizvoljnog ravanskog sistema sila, potrebno je i dovoljno, da mu sume momenata svih sila, za proizvoljno izabrane tačke A, B i C u ravni dejstva, koje ne leže na istoj pravoj, budu jednake nuli. 24. 10. 2020. 30

◦ Uslovi ravnoteže ravanskog sistema sila i ravanskog sistema spregova: Uslovi ravnoteže ravanskog sistema od n sila i ravanskog siatema od s spregova glase 24. 10. 2020. 31

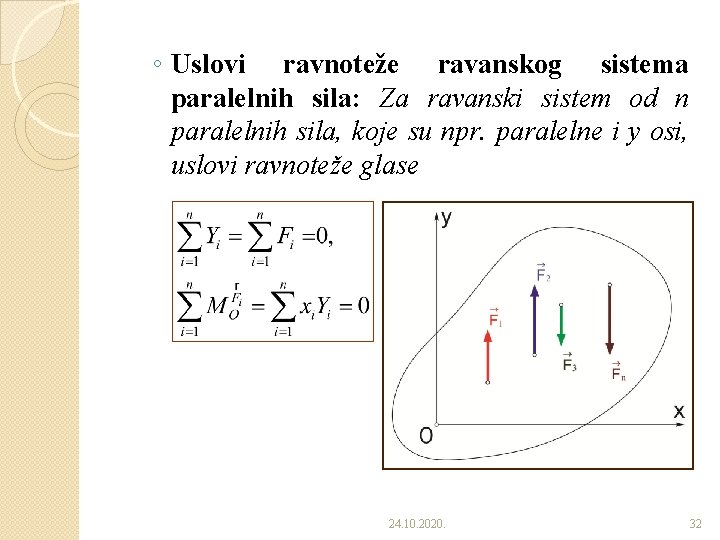
◦ Uslovi ravnoteže ravanskog sistema paralelnih sila: Za ravanski sistem od n paralelnih sila, koje su npr. paralelne i y osi, uslovi ravnoteže glase 24. 10. 2020. 32

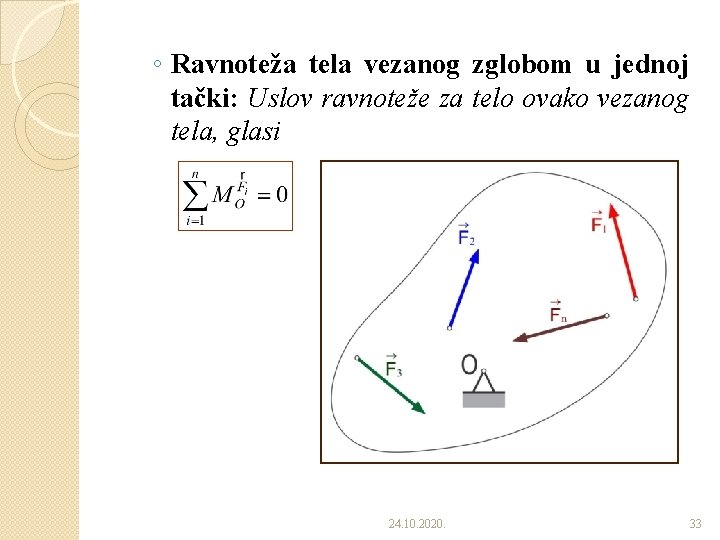
◦ Ravnoteža tela vezanog zglobom u jednoj tački: Uslov ravnoteže za telo ovako vezanog tela, glasi 24. 10. 2020. 33

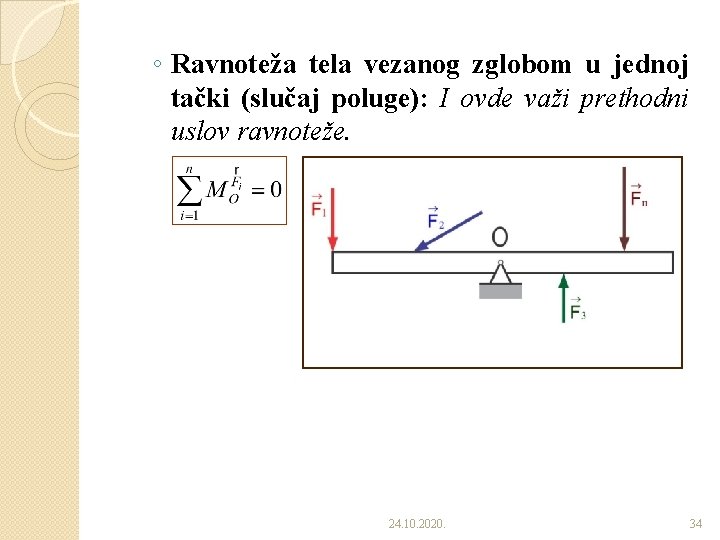
◦ Ravnoteža tela vezanog zglobom u jednoj tački (slučaj poluge): I ovde važi prethodni uslov ravnoteže. 24. 10. 2020. 34

�Stabilnost ravnotežnog stanja krutog tela ◦ Ako su glavni vektor i glavni moment krutog tela, izloženog delovanju proizvoljnog ravanskog sistema sila, jednaki nuli (0), za takvo telo kažemo da se nalazi u ravnoteži. ◦ Kakvoj ravnoteži? �Stabilnoj, �Nestabilnoj (labilnoj) ili �Indiferentnoj. 24. 10. 2020. 35

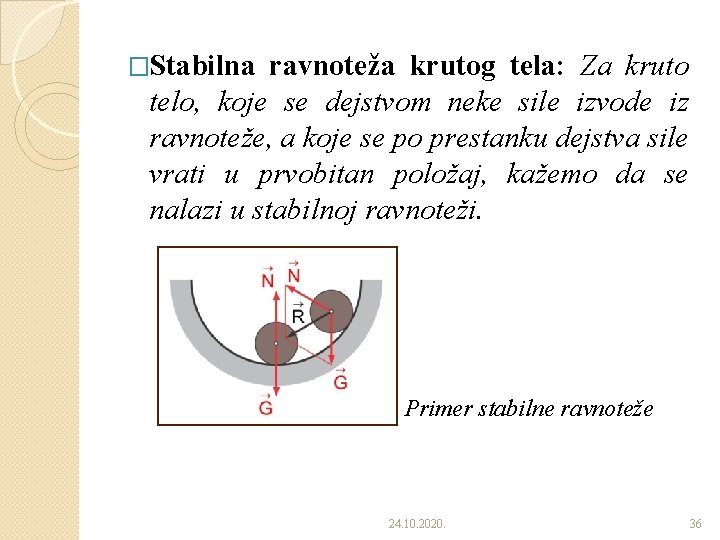
�Stabilna ravnoteža krutog tela: Za kruto telo, koje se dejstvom neke sile izvode iz ravnoteže, a koje se po prestanku dejstva sile vrati u prvobitan položaj, kažemo da se nalazi u stabilnoj ravnoteži. Primer stabilne ravnoteže 24. 10. 2020. 36

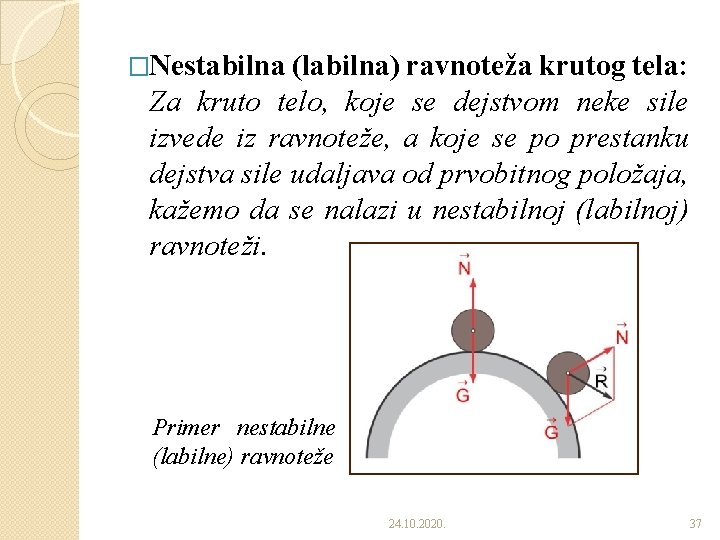
�Nestabilna (labilna) ravnoteža krutog tela: Za kruto telo, koje se dejstvom neke sile izvede iz ravnoteže, a koje se po prestanku dejstva sile udaljava od prvobitnog položaja, kažemo da se nalazi u nestabilnoj (labilnoj) ravnoteži. Primer nestabilne (labilne) ravnoteže 24. 10. 2020. 37

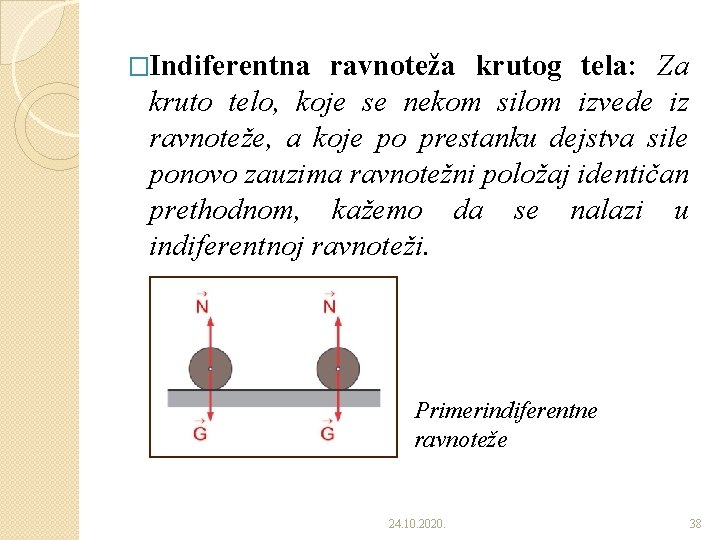
�Indiferentna ravnoteža krutog tela: Za kruto telo, koje se nekom silom izvede iz ravnoteže, a koje po prestanku dejstva sile ponovo zauzima ravnotežni položaj identičan prethodnom, kažemo da se nalazi u indiferentnoj ravnoteži. Primerindiferentne ravnoteže 24. 10. 2020. 38

RAVNOTEŽA SISTEMA KRUTIH TELA �Do sada smo u razmatranje uzimali jedno kruto telo. �Međutim, statički proračuni različitih konstrukcija, sačinjenih od više krutih tela, često se svode na razmatranje ravnoteže konstrukcije u celosti. �Veze kojima su spojena tela u sistem mogu biti spoljašnje i unutrašnje. 24. 10. 2020. 39

�Prema zakonu akcije i reakcije (Aksiom 4) pri oslobađanju od unutrašnjih veza imamo reakcije u paru koje su jednake po intenzitetu, a smerovi su im suprotni. �Pri oslobađanju od spoljašnjih veza reakcije se svode na jednu silu �Ako se oslobodimo samo spoljašnjih veza, pri razmatranju ravnoteže, reakcije unutrašnjih veza se ne uzimaju u obzir (ravnotežu sistema tela, odnosno konstrukcije, posmatramo u celosti). 24. 10. 2020. 40

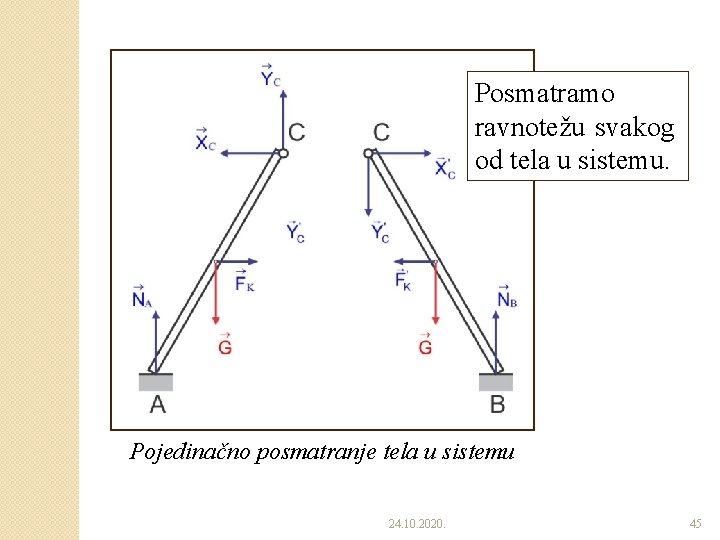
�Oslobađanjem od spoljašnjih i unutrašnjih veza, vodeći računa o parnosti reakcija unutrašnjih veza, možemo posmatrati ravnotežu svakog pojedinačnog tela u sistemu. 24. 10. 2020. 41

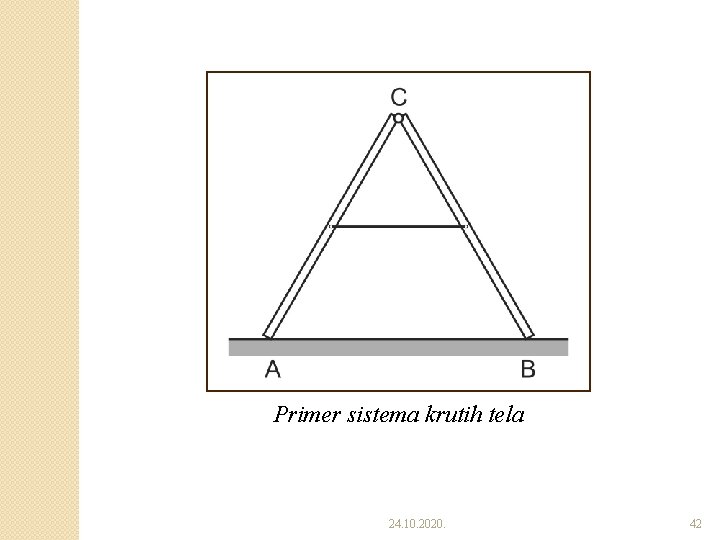
Primer sistema krutih tela 24. 10. 2020. 42

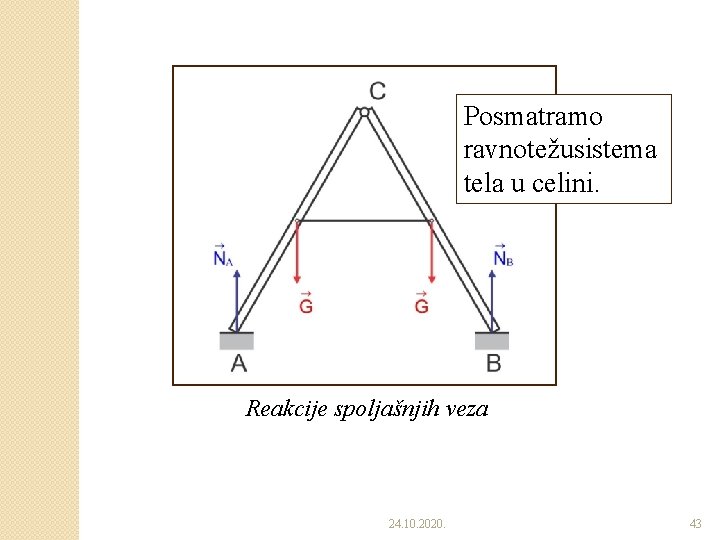
Posmatramo ravnotežusistema tela u celini. Reakcije spoljašnjih veza 24. 10. 2020. 43

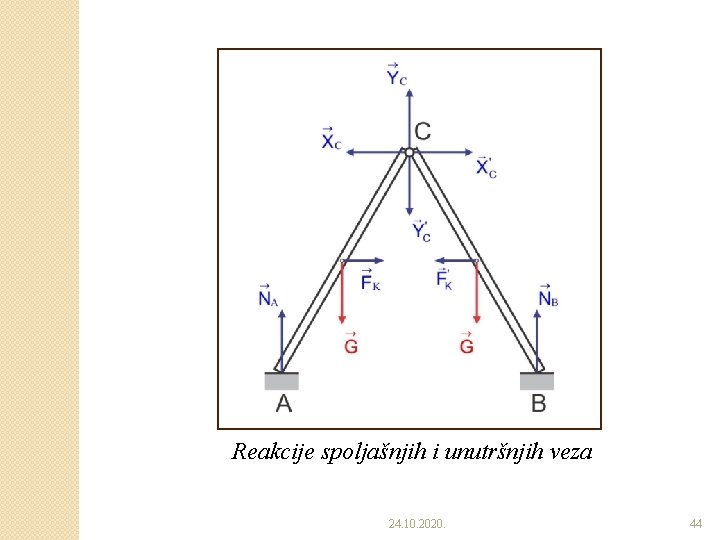
Reakcije spoljašnjih i unutršnjih veza 24. 10. 2020. 44

Posmatramo ravnotežu svakog od tela u sistemu. Pojedinačno posmatranje tela u sistemu 24. 10. 2020. 45