Meet the Neurons Models of the brain hardware

Meet the Neurons Models of the brain hardware

A Real Neuron The Neuron

Mcculloch-pitts 1940’s • • • Y = f(next) = f( S wi xi + b) Wi are weights Xi are inputs B is a bias term F() is activation function – F = 1 if next >= 0 else -1

Activation Functions Modified Mcculloch-pitts • The function shown before is a threshold function • Tanh function • Logistic

Human Brain • Neuron Speed - 10 -3 seconds per operation • Brain weights about 3 pounds and at rest consumes 20% of the bodies oxygen. • Estimates place neuron count at 1012 to 1014 • Connectivity can be 10, 000

What is the capacity of the brain? • Estimate the MIPS of a brain • Estimate the MIPS needed by a computer to simulate the brain

Structure • The cortex is estimated to be 6 layers • The brain does recognition type computations is 100 -200 milliseconds • The brain clearly uses some specialized structures.

Survey of Artificial Neural Networks
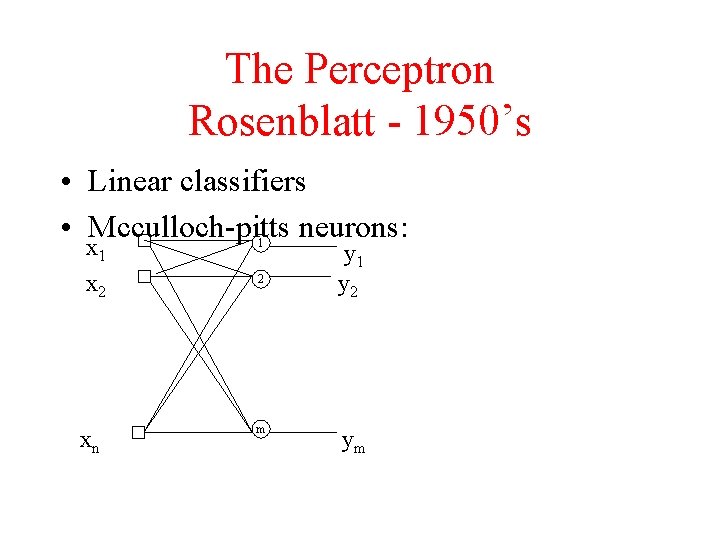
The Perceptron Rosenblatt - 1950’s • Linear classifiers • Mcculloch-pitts neurons: x 1 1 x 2 2 xn m y 1 y 2 ym
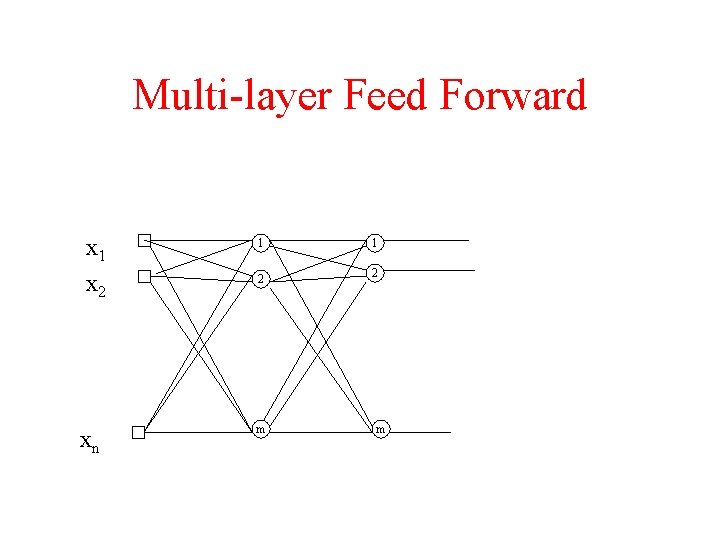
Multi-layer Feed Forward x 1 1 1 x 2 2 2 xn m m

Training Vs. Learning • Learning is ‘self directed” • Training is externally controlled – Set of pairs of inputs and desired outputs

Learning Vs. Training • Hebbian learning: – Strengthen connections that are fired at same time • Training: – Back propagation – Hopfield networks – Boltzman machines

Back Propagation • Present input then measure desired vs. . Actual outputs • Correct weights by back propagating error though net • Hidden layers are corrected in proportion to the weight they provide to output stage. • Need a constant, used to prevent rapid training

Back Propagation The Math • Number the Levels: – 0 is input – N is output – All neurons in level i is connected to each neuron in i+1 • Weights from level i to i+1 form a matrix Wi • Input is a vector x and Training data is a vector t • The vector yi is the input to level i: – y 0 = x – yi+1 = fi ( Wi * yi + bi)

The Math (cont. ) • Error is dn= t – yn • Back propagate the error – di = (WTi+1 di+1) (fi(net)) – Where WT is a transpose matrix of W • Update the W matrices and bias terms – DWi = a di y. Ti-1 D bi = a di b

Hopfield Networks • • Single layer Each neuron receives and input Each neuron has connections to all others Training by “clamping” and adjusting weights

Boltzman Machines • Change f() in Mc. Culloch-Pitts to be probabilistic • The energy gap between 0 and 1 outputs is related to a “temperature” • pk = 1 / [ 1 + e t] t = -DEk / T • Learning: – Hold inputs and outputs according to training data – Anneal temperature while adjusting weights

PDP - an turning point • Parallel Distributed Processing (1985) • Properties: – Learning similar to observed human behavior – Knowledge is distributed! – Robust

Connectionism • Superposition principle – Distributed “knowledge representation” • Separation of process and “knowledge representation” • Knowledge representation is not symbolic in the same sense as symbolic AI!

Example 1 • • Face recognition – Gary Cottrell Input a 64 x 64 grid Hidden layer 80 neurons Output layer 8 neurons – face yes, no, 2 bits for gender and 5 bits for name • Results: – Recognized the input set – 100% – Face / no-face on new faces – 100% – Male / female determination on new faces – 81%

Example 2 • SRI worked on a net to spot tanks • Used pictures of tanks and non-tanks • Pictures were both exposed and hidden vehicles! • When it worked, exposed it to new pictures • It failed! Why?

Example 3 The nature of Sub-symbolic • Categorize words by lexical type based on word order (Elman 1991)
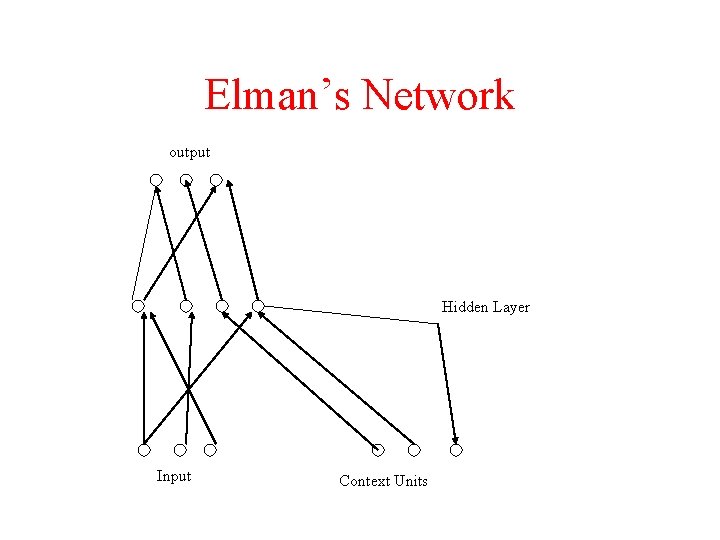
Elman’s Network output Hidden Layer Input Context Units

Training • Set build from sample sentences – 29 words – 10, 000 two and three word sentences – Training sample is input word and following word pair • No unique answer – output is a set of words • Analysis of the trained network – – No symbol in the hidden layer corresponding to words or word pairs!!

Connectionisms challenge • Fodor’s Language of the Mind • Folk Psychology – mind states and our tags for them • How does the brain get to these? • Marr’s type 1 theory – competence with out explanations • See Associative Engines by Andy Clark for more!

Pulsed Systems • Real neurons pulse! • Pulsed neurons have computing power over level

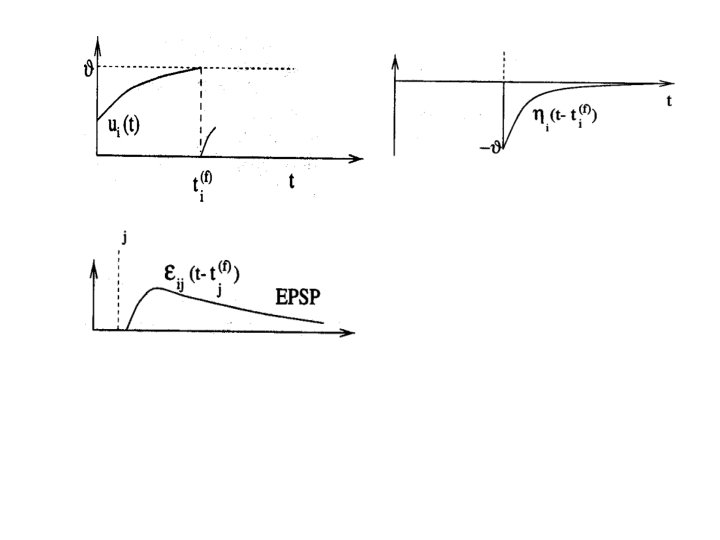
Spike Response Model • Variable ui describes the internal state • Firing times are: – Fi = {ti(f) ; i< f < n} = {t | ui(t) = threshold } – After a spike, the state variable's value is lowered • Inputs – ui= S wij eij(t - tj(f))

Models • Full Models – Simulate continuous functions – Can integrate other factors • Currents other than dendrite • Chemical states • Spike Models – Simplify and treat output as an impulse

Computational Power • Spiked Neurons Power – All the neurons are Turing Computable – Can do some things cheaper in neuron count

Encoding Problem • How does the human brain use the spike trains? • Rate Coding – Spike density – Rate over population • Pulse Coding – Time to first spike – Phase – Correlation

Where Next? • Build a brain model! • Analyze the operation of real brains

Interesting Work • Computational Cockroach by Randall D Beer • Systems of Igor Aleksander – Imagination and Consciousness • Cat brain of Hugo De. Grais
- Slides: 33