Medidas e Incertezas Experimentais George C Cardoso Mea


























- Slides: 36

Medidas e Incertezas Experimentais George C. Cardoso

“Meça o que mensurável e faça mensurável o que não é” Galileu Essa filosofia forma a base da ciência e tecnologia moderna. Esta filosofia permitiu o surgimento do método científico e o desenvolvimento da engenharia e produção em massa. O método científico visa minimizar a subjetividade, quantificando tanto o que é observado quanto a incerteza do observável.

Vamos medir (contar) o numero de laranjas • Quantas laranjas tem aí? • Incerteza? • Conte de novo algumas vezes? • Peça para outra pessoa contar.

Quantas bactérias tem nessa imagem? • Conte numa certa região. • Conte novamente. • Peça para outra pessoa contar. • Muda de medida para medida? • Qual a variação?

Medir é medir o valor médio. Melhor que isso, só se a quantidade medida puder ser contada. Usar técnicas de medida diferentes e comparar resultados para evitar inconsistências

Medindo o diâmetro de uma moeda: Lifehacker On. Fire. Guy Resolução ~ 1 mm Baixa precisão ~ 0, 5 cm Resolução ~ 0, 5 mm Média precisão ~ 0, 1 mm Banggood Resolução ~ 0, 01 mm Alta precisão ~ 0, 01 mm

Vamos “medir” a largura desta sala • O que é medir? Calcular o valor médio de estimativas • Vamos estimar o valor médio que vocês acham que esta parede tem (em metros ou metros e fração de metros). • Cada um – independentemente --estima a largura da melhor forma possível. • Anote o valor sem discutir com os colegas para nao enviesar a sua estimativa.

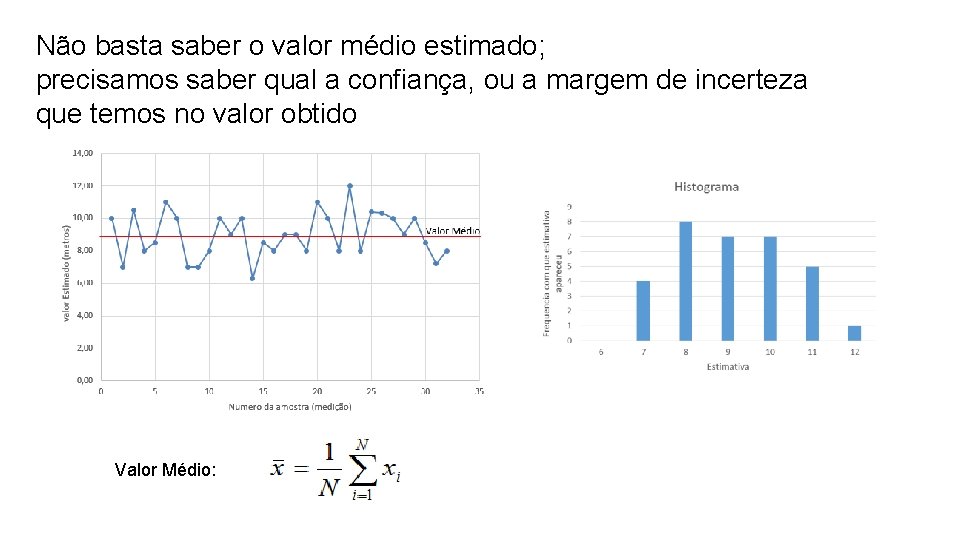
Não basta saber o valor médio estimado; precisamos saber qual a confiança, ou a margem de incerteza que temos no valor obtido Valor Médio:

Medida da largura da sala (olhômetro) https: //support. office. com/en-us/article/Create-a-histogram-b 6814 e 9 e-5860 -4113 -ba 51 -e 3 a 1 b 9 ee 1 bbe Resultados escritos em termos Do valor médio e desvio padrão: (9, 0 ± 1, 4) metros, n = 32 Primeiro escrevemos O desvio padrão com 1 algarismo ou 2 algarismos Significativos no caso do primeiro Dígito ser 1. Valor Médio: = 8, 9759 m Desvio padrão da amostra: = 1, 3940 m Depois, olhando para os algarismos significativos E para a posição da vírgula, se houver, escrevemos O valor da média arredondado até o algarismo correspondente Ao menor algarismo significativo do desvio padrão. Neste exemplo, O menor algarismo significativo do desvio padrão é 4 e fica logo Depois da vírgula. Assim, paramos o arredondamento da média Logo depois da vírgula. Resultado medido com a trena: 8, 9 metros

Desvio Padrão amostral: s • Variância (s 2) é a “potência média” da variação de medida para medida em torno da média. • Desvio padrão (s) tem as mesmas da quantidade medida. Exemplo: se a medida for em metros, o desvio padrão estará em metros.

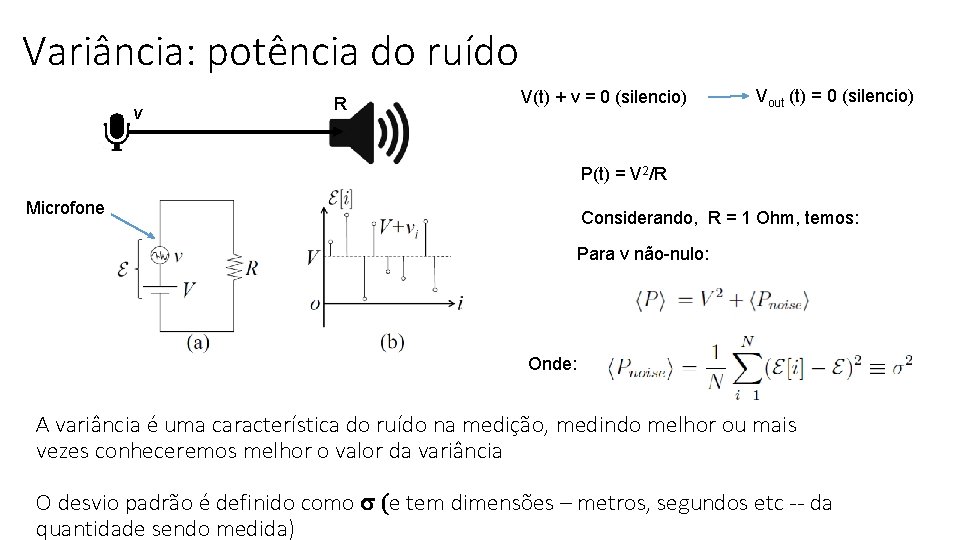
Variância: potência do ruído v R V(t) + v = 0 (silencio) Vout (t) = 0 (silencio) P(t) = V 2/R Microfone Considerando, R = 1 Ohm, temos: Para v não-nulo: Onde: A variância é uma característica do ruído na medição, medindo melhor ou mais vezes conheceremos melhor o valor da variância O desvio padrão é definido como s (e tem dimensões – metros, segundos etc -- da quantidade sendo medida)

Para duas quantidades com ruído, somadas, a variância se soma: Microfone 1 Microfone 2 Assim, a variância da soma é a soma das variâncias:

2 s Variância de uma medida: “potencia média” da flutuação ou ruído da medida A variância é uma característica combinada do processo, condições de medida e habilidade dos experimentadores. Medir mais vezes sem fazer nenhuma mudança não vai diminuir a variância/ruído, Mas vai permitir uma melhor caracterização da variância (obter a variância com mais algarismos significativos) A variância tem unidade do quadrado das unidades medidas. Exemplo: se a quantidade medida foi mm, a variância será em mm 2 s (a raiz quadrada da variância) é chamado de desvio padrão e tem as mesmas unidades utilizadas na medida.

Medida da largura da sala (olhômetro) https: //support. office. com/en-us/article/Create-a-histogram-b 6814 e 9 e-5860 -4113 -ba 51 -e 3 a 1 b 9 ee 1 bbe Resultados escritos em termos Do valor médio e desvio padrão: (9, 0 ± 1, 4) metros, n = 32 Primeiro escrevemos O desvio padrão com 1 algarismo ou 2 algarismos Significativos no caso do primeiro Dígito ser 1. Valor Médio: = 8, 9759 m Desvio padrão da amostra: = 1, 3940 m Depois, olhando para os algarismos significativos E para a posição da vírgula, se houver, escrevemos O valor da média arredondado até o algarismo correspondente Ao menor algarismo significativo do desvio padrão. Neste exemplo, O menor algarismo significativo do desvio padrão é 4 e fica logo Depois da vírgula. Assim, paramos o arredondamento da média Logo depois da vírgula. Resultado medido com a trena: 8, 9 metros

Desvio padrão da média (erro padrão) Suponha que você tem n baterias (ou medidas) do mesmo tipo, todas com ruído do mesmo tipo. Qual o desvio padrão do valor médio destas baterias (ou medidas)? Desvio padrão da média

Desvio padrão da média (erro padrão) Significado: Se repetirmos o experimento de N medidas, qual a flutuação no valor médio obtido. Exemplo: Se perguntarmos para outras classes similares e com o mesmo numero de alunos estimando a largura da parede, qual seria o desvio padrão dos valores médios encontrados? Ou seja, como flutua esse valor médio quando repetimos o experimento? x = (9, 0 ± 0, 2) metros, I. C. 68% I. C. significa “intervalo de confiança”

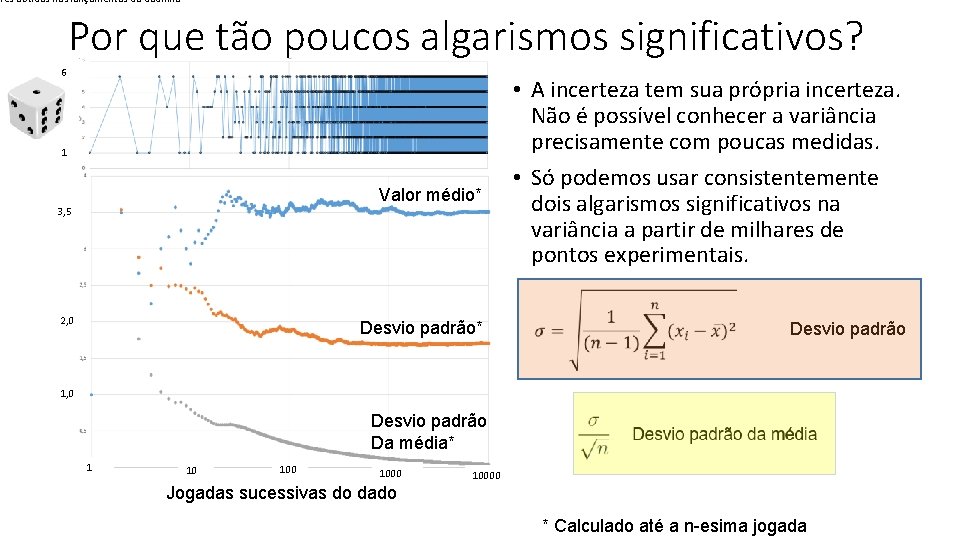
res obtidos nos lançamentos do dadinho Por que tão poucos algarismos significativos? 6 1 Valor médio* 3, 5 • A incerteza tem sua própria incerteza. Não é possível conhecer a variância precisamente com poucas medidas. • Só podemos usar consistentemente dois algarismos significativos na variância a partir de milhares de pontos experimentais. 2, 0 Desvio padrão* Desvio padrão 1, 0 Desvio padrão Da média* 1 10 10000 Jogadas sucessivas do dado * Calculado até a n-esima jogada

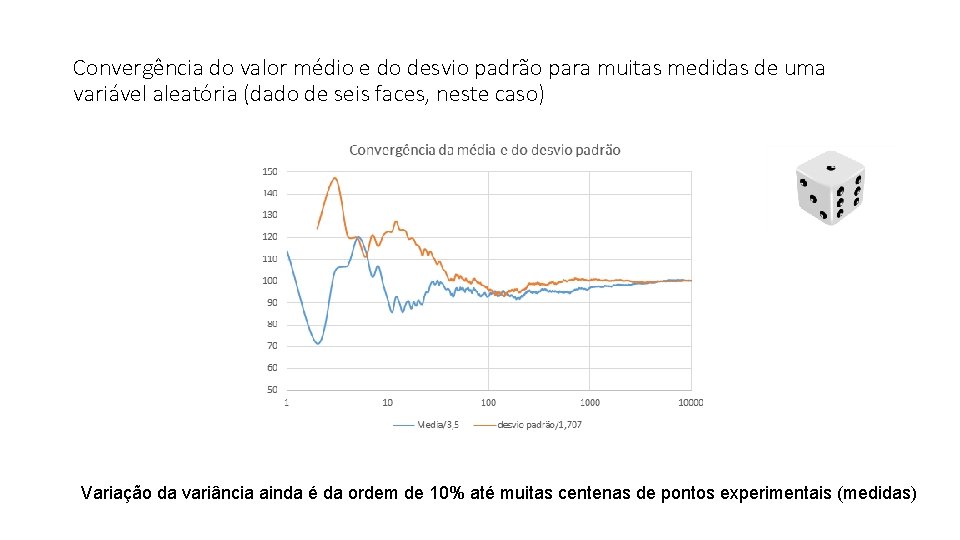
Convergência do valor médio e do desvio padrão para muitas medidas de uma variável aleatória (dado de seis faces, neste caso) Variação da variância ainda é da ordem de 10% até muitas centenas de pontos experimentais (medidas)

Caso especial de arredondamento (incerteza começando com 1, e N<1000) No caso da incerteza começar com 1 manter 2 alg. Sig. Se a incerteza começar com 2, 3, . . . , 9, basta 1 alg. sig. Valor Médio: 23, 456 Incerteza : 0, 145 0, 15 Como escrever: (23, 46 ± 0, 15) unidades Se a incerteza começar com algarismo diferente de 1, usar somente 1 alg significativo. Exemplo: (14, 29 ± 0, 33) fica escrito como: (14, 3 ± 0, 3)

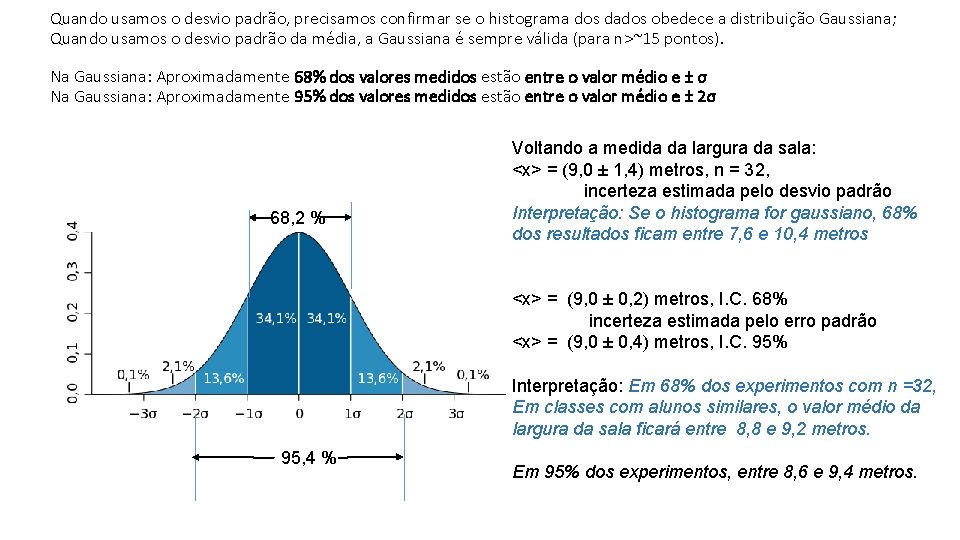
Quando usamos o desvio padrão, precisamos confirmar se o histograma dos dados obedece a distribuição Gaussiana; Quando usamos o desvio padrão da média, a Gaussiana é sempre válida (para n>~15 pontos). Na Gaussiana: Aproximadamente 68% dos valores medidos estão entre o valor médio e ± σ Na Gaussiana: Aproximadamente 95% dos valores medidos estão entre o valor médio e ± 2σ 68, 2 % Voltando a medida da largura da sala: <x> = (9, 0 ± 1, 4) metros, n = 32, incerteza estimada pelo desvio padrão Interpretação: Se o histograma for gaussiano, 68% dos resultados ficam entre 7, 6 e 10, 4 metros <x> = (9, 0 ± 0, 2) metros, I. C. 68% incerteza estimada pelo erro padrão <x> = (9, 0 ± 0, 4) metros, I. C. 95% Interpretação: Em 68% dos experimentos com n =32, Em classes com alunos similares, o valor médio da largura da sala ficará entre 8, 8 e 9, 2 metros. 95, 4 % Em 95% dos experimentos, entre 8, 6 e 9, 4 metros.

Erro padrão (desvio padrão da média) Desvio padrão da média (incerteza da média) 68, 2 % Se distribuição for Gaussiana: 68% dos experimentos com mesmo N terão média encontrada no intervalo: (<x> ± ). 95, 4 % 95% dos experimentos com mesmo N terão média encontrada no intervalo: (<x> ± 2 ) NOTE: Se o número de medições N ∞ você encontra a média Verdadeira para o tipo de medida feita.

Calculando o perímetro da sala: Seja <x> = (9, 0 ± 0, 4) m, I. C. 95% Seja <y> = (10, 0 ± 0, 3) m, I. C. 95% P = 2(x + y) Somar as médias de forma convencional e os desvios padrão conforme: Assim: P = 2*(19, 0 ± 0, 5) m, I. C. 95% P = (38, 0 ± 1, 0) m, I. C. 95%

Calculando a área da sala: Seja <x> = (9, 0 ± 0, 4) m, I. C. 95% Seja <y> = (10, 0 ± 0, 3) m, I. C. 95% A = x*y Calcula-se a área média de forma convencional <A> = 9*10 = 90 m 2 As incertezas são calculadas de acordo com σA 2= δA(x + δx, y)2 + δA(x, y + δy) 2 σA 2= (A(x + δx, y) - <A>)2 + (A(x, y + δ y) - <A>)2 = (9, 4*10 – 90)2 + (9, 0*10, 3 – 90)2 = 42 + 2, 72 = 23, 29 σA = 4, 82 <A> = (90, 0 ± 4, 82) <A> = (90 ± 5) m 2, I. C. 95%

Como diminuir a incerteza no valor médio? <A> = (90 ± 5) m 2, I. C. 95% Como fazer com que a incerteza fique abaixo de 1 m 2 • Melhorar a técnica de medida sem mudar o numero de leituras (exemplo: usar uma boa trena, trena laser, etc) • Ou Medir mais vezes para melhorar a média. • Se com n = 32 obtivemos a incerteza de 5 m 2, quantas medidas precisamos fazer para ter igual a 1 m 2 ?

• Nota: Se quisermos diminuir a incerteza no valor médio (desvio padrão da média, também conhecido como erro padrão) em 10 vezes, temos que fazer 100 vezes mais medições. O desvio padrão, por outro lado, é uma caractecterística do ruído e é simplesmente ligado a variância, ou seja, a quanto variam as medidas. Medir mais vezes simplesmente permite melhor conhecer quanto vale essa variação.

Representação do Resultado e Algarismos Significativos: olhar primeiro para a incerteza da medida. Exemplo 1: Incerteza : 0, 345 Para < 1000 medidas so teremos um algarismo significativo (máximo 2) Valor Médio: 23, 456 Incerteza : 0, 3 Valor Médio: 23, 5 (note que os números estão arredondados para o numero correto de alg. Sig. ) Como escrever: (23, 5 ± 0, 3) o. C Exemplo 2: Incerteza : 15, 345 Para < 1000 medidas so teremos um algarismo significativo (máximo 2) Valor Médio: 141, 235 Incerteza : 15 (aqui guardamos 2 algarismos significativos porque se arredondássemos para baixo seria uma mudança de 50%, que é maior que a incerteza da incerteza) Valor Médio: 141 (note que os números estão arredondados para o numero correto de alg. Sig. ) Como escrever: (141 ± 15) o. C

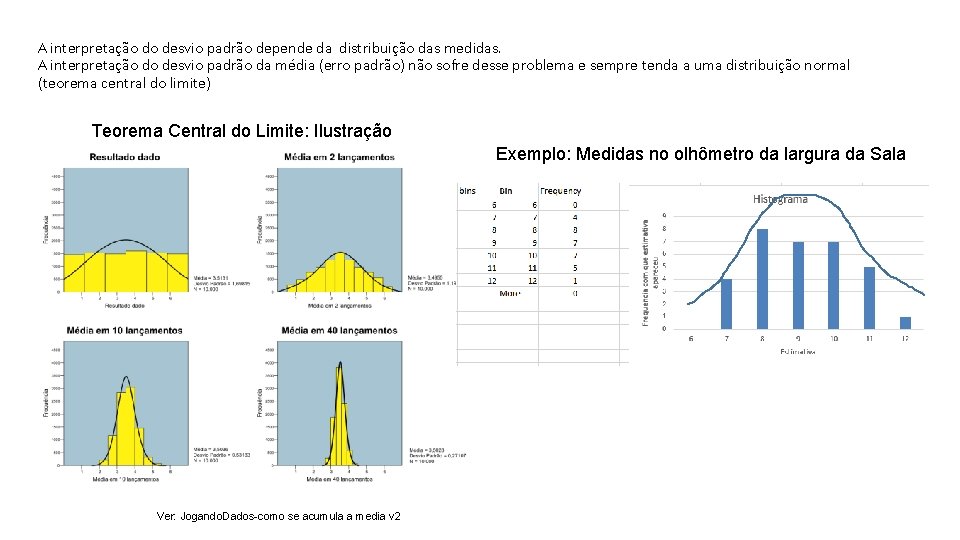
A interpretação do desvio padrão depende da distribuição das medidas. A interpretação do desvio padrão da média (erro padrão) não sofre desse problema e sempre tenda a uma distribuição normal (teorema central do limite) Teorema Central do Limite: Ilustração Exemplo: Medidas no olhômetro da largura da Sala Ver: Jogando. Dados-como se acumula a media v 2

Voltando ao problema da medida da largura da sala de aula • Obtivemos (9, 0 ± 1, 4) metros, n = 32 • O que é a média verdadeira? A média verdadeira seria a média que encontraríamos se medíssemos um número infinito de vezes, ou seja n infinito. Isso não conseguimos fazer na prática. • Sabemos que o desvio padrão é uma característica do processo de medida. Ele vai se manter da mesma ordem de grandeza do que já temos, ou seja, da ordem de 1 metro, mesmo com n muito grande. • Repetições para produzir estatística das medidas nao conseguem avaliar se a técnica de medida é adequada ou correta. Para isso precisamos usar diferentes técnicas de medida e comparar os resultados.

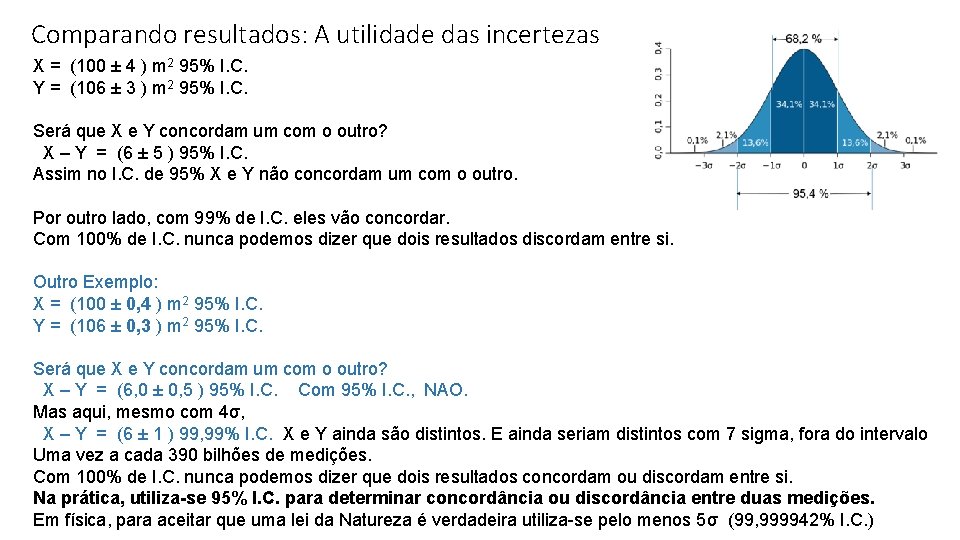
Comparando resultados: A utilidade das incertezas X = (100 ± 4 ) m 2 95% I. C. Y = (106 ± 3 ) m 2 95% I. C. Será que X e Y concordam um com o outro? X – Y = (6 ± 5 ) 95% I. C. Assim no I. C. de 95% X e Y não concordam um com o outro. Por outro lado, com 99% de I. C. eles vão concordar. Com 100% de I. C. nunca podemos dizer que dois resultados discordam entre si. Outro Exemplo: X = (100 ± 0, 4 ) m 2 95% I. C. Y = (106 ± 0, 3 ) m 2 95% I. C. Será que X e Y concordam um com o outro? X – Y = (6, 0 ± 0, 5 ) 95% I. C. Com 95% I. C. , NAO. Mas aqui, mesmo com 4σ, X – Y = (6 ± 1 ) 99, 99% I. C. X e Y ainda são distintos. E ainda seriam distintos com 7 sigma, fora do intervalo Uma vez a cada 390 bilhões de medições. Com 100% de I. C. nunca podemos dizer que dois resultados concordam ou discordam entre si. Na prática, utiliza-se 95% I. C. para determinar concordância ou discordância entre duas medições. Em física, para aceitar que uma lei da Natureza é verdadeira utiliza-se pelo menos 5σ (99, 999942% I. C. )

Incertezas se somam mesmo nas diferenças de valores

Leitura suplementar

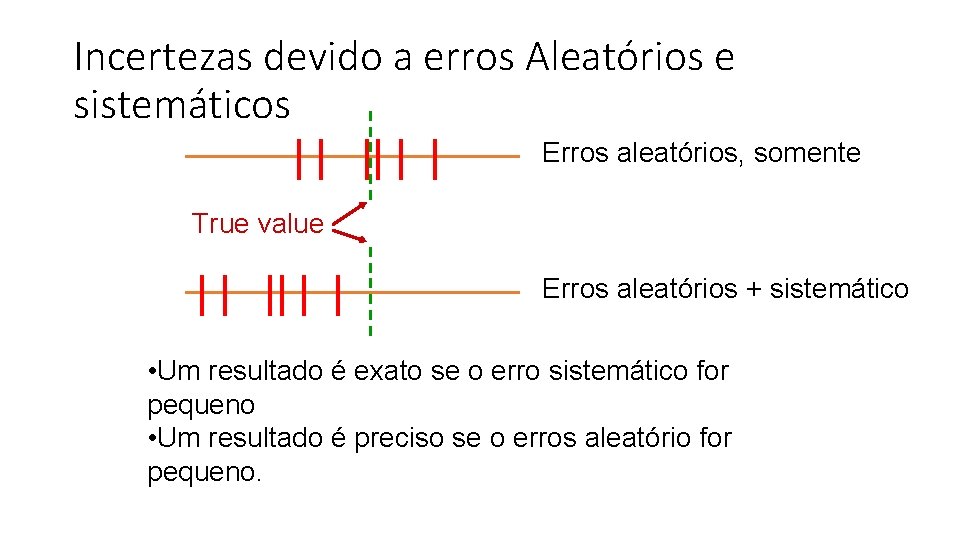
Incerteza aleatório vs. sistemático • Aleatório (incerteza): tende a variar a cada medida, tanto para mais quanto para menos. Na maioria dos casos forma uma distribuição Gaussiana em torno da média. O erro aleatório está sempre presente nas medidas. O erro aleatório pode ser minimizado fazendo-se muitas médias, melhorando método experimental para minimizar variância e/ou medindo-se a variável em função de outra e fazendo ajuste de curva. • Sistemático: erros de calibração e de método. Difícil de detectar. Somas destes erros são somas lineares. ANALISE ESTATISTICA não detecta este erro. Esse erro pode ser detectada utilizando-se métodos alternativos e comparando resultados. • Assume-se que não existem enganos nem erros crassos. Supõe-se que o experimentalista é cuidadoso (da mesma forma que se assume que os cálculos num artigo ou relatório cientifico estão corretos, o que nem sempre é verdade. )

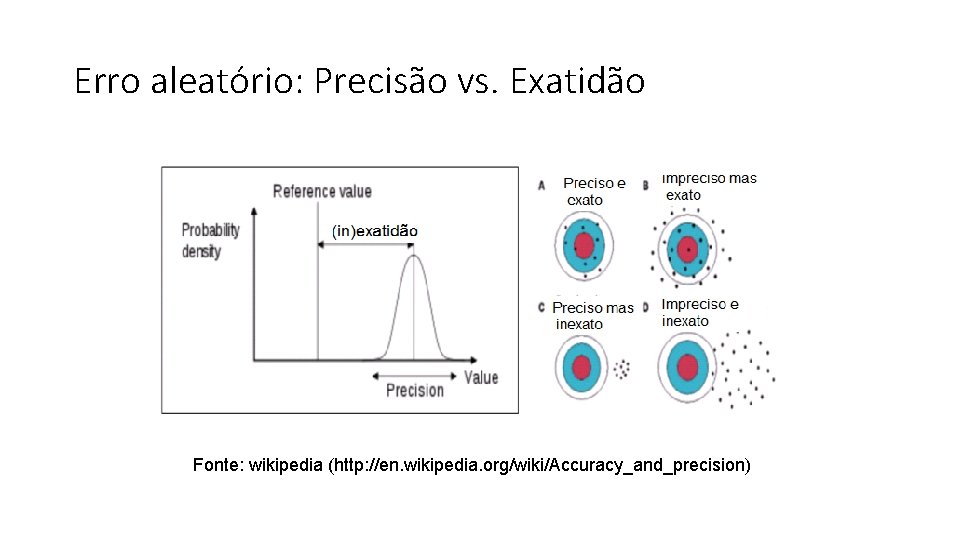
Erro aleatório: Precisão vs. Exatidão Fonte: wikipedia (http: //en. wikipedia. org/wiki/Accuracy_and_precision)

Discuta com seu colega a precisão e exatidao de cada figura

Incertezas em vários instrumentos de medida Incerteza de leitura: ½ da menor divisão Qual a incerteza nesse multimetro? Cuidado com Paralaxe: em instrumentos de ponteiros e Reguas. Instrumentos digitais: Ver manual do fabricante. Metade do digito que contém incerteza ou metade Do ultimo digito caso nenhum digito apresentado tenha incerteza.

Incertezas devido a erros Aleatórios e sistemáticos Erros aleatórios, somente True value Erros aleatórios + sistemático • Um resultado é exato se o erro sistemático for pequeno • Um resultado é preciso se o erros aleatório for pequeno.
 Pesquisa quase experimental
Pesquisa quase experimental Judith cardoso
Judith cardoso Josie cardoso rojo
Josie cardoso rojo Dra fernanda cardoso
Dra fernanda cardoso Dr jorge cardoso
Dr jorge cardoso Edite cardoso ginecologista
Edite cardoso ginecologista Propagação de erro divisão
Propagação de erro divisão George washington vs king george iii venn diagram
George washington vs king george iii venn diagram George washington vs king george iii
George washington vs king george iii Limba romana este patria mea eseu
Limba romana este patria mea eseu Zona mea
Zona mea Vulnerasti cor meum soror mea sponsa
Vulnerasti cor meum soror mea sponsa Roman familia
Roman familia Down l
Down l Mie dor mie dor de casa mea
Mie dor mie dor de casa mea Mea bombardelli
Mea bombardelli Anette sundqvist
Anette sundqvist Lauda mea e pentru împăratul versuri
Lauda mea e pentru împăratul versuri Roada duhului bucuria
Roada duhului bucuria Iucundum mea vita mihi proponis amorem
Iucundum mea vita mihi proponis amorem Mea parte de vorbire
Mea parte de vorbire Isuse viata mea scump tezaur
Isuse viata mea scump tezaur Familia declinazione
Familia declinazione Vreau sa te cunosc mai mult versuri
Vreau sa te cunosc mai mult versuri O cântare de mărire am în inimă mereu
O cântare de mărire am în inimă mereu Revista mea personajul meu preferat
Revista mea personajul meu preferat Mea culpa meaning
Mea culpa meaning Vulnerasti cor meum significato
Vulnerasti cor meum significato Am zidit un altar versuri
Am zidit un altar versuri En tine
En tine Familia declinazione
Familia declinazione Mai frumos nici ingerii nu canta
Mai frumos nici ingerii nu canta Credința mea eu o zidesc
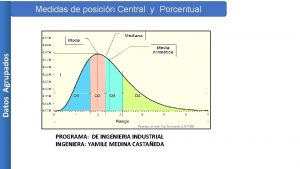
Credința mea eu o zidesc Medidas de posición
Medidas de posición Paralelas educacion fisica
Paralelas educacion fisica Perimetro cefalico recien nacido
Perimetro cefalico recien nacido Caracteristicas de la mediana
Caracteristicas de la mediana