Medidas de Dispersin se llaman medidas de dispersin

Medidas de Dispersión: se llaman medidas de dispersión aquellas que permiten retratar la distancia de los valores de la variable a un cierto valor central, o que permiten identificar la concentración de los datos en un cierto sector del recorrido de la variable. Se trata de coeficientes para variables cuantitativas. Las más usuales son el desvío estándar y la varianza

Medidas de Dispersión •

La desviación estándar. Una medida diferencial para identificar esos conjuntos de datos es la concentración o dispersión alrededor de la media. Una manera de evitar que los distintos signos se compensen es elevarlas al cuadrado, de manera que todas las desviaciones sean positivas. La raíz cuadrada del promedio de estas cantidades recibe el nombre de desviación estándar, o desviación típica y es representada por la siguiente fórmula:

. La Varianza El cuadrado de la desviación estándar recibe el nombre de varianza y se representa por. La suma de los cuadrados de los desvíos de la totalidad de las observaciones, respecto de la media aritmética de la distribución, es menor que la suma de los cuadrados de los desvíos respecto de cualquier otro valor que no sea la media aritmética. Si observamos, veremos que la varianza no es más que el desvío estándar al cuadrado. Precisamente la manera de simbolizarla es. Por lo mismo, la desviación estándar puede definirse como la raíz cuadrada de la varianza

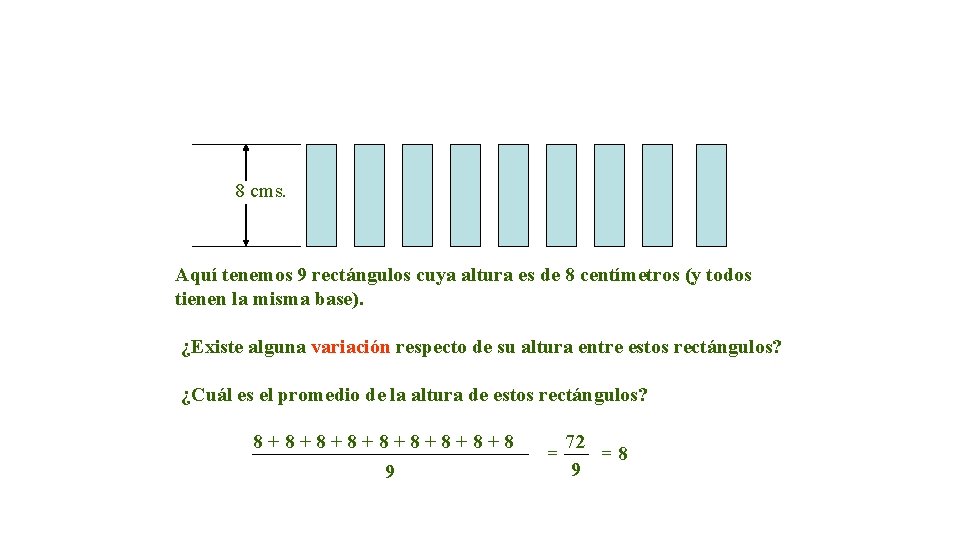
8 cms. Aquí tenemos 9 rectángulos cuya altura es de 8 centímetros (y todos tienen la misma base). ¿Existe alguna variación respecto de su altura entre estos rectángulos? ¿Cuál es el promedio de la altura de estos rectángulos? 8+8+8+8+8 9 = 72 =8 9

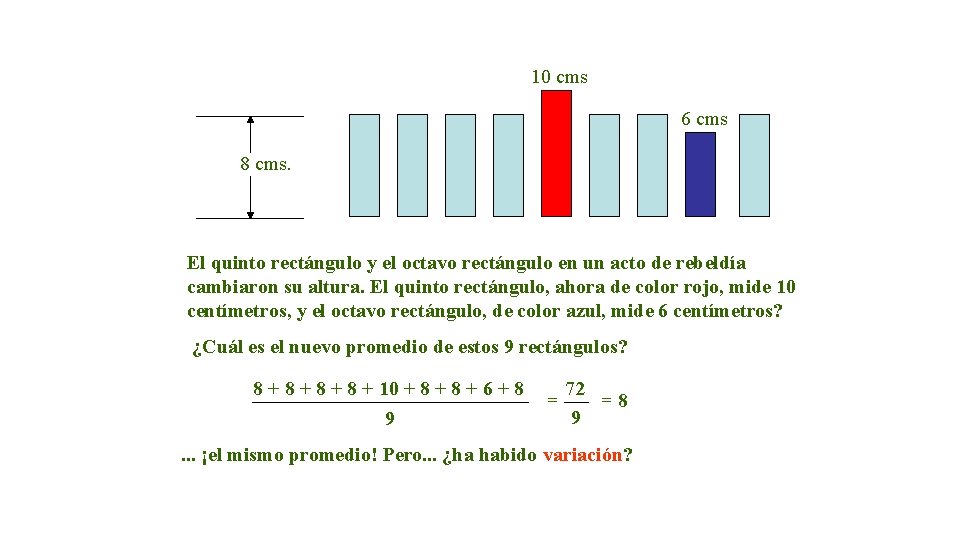
10 cms 6 cms 8 cms. El quinto rectángulo y el octavo rectángulo en un acto de rebeldía cambiaron su altura. El quinto rectángulo, ahora de color rojo, mide 10 centímetros, y el octavo rectángulo, de color azul, mide 6 centímetros? ¿Cuál es el nuevo promedio de estos 9 rectángulos? 8 + 8 + 10 + 8 + 6 + 8 9 = 72 =8 9 . . . ¡el mismo promedio! Pero. . . ¿ha habido variación?

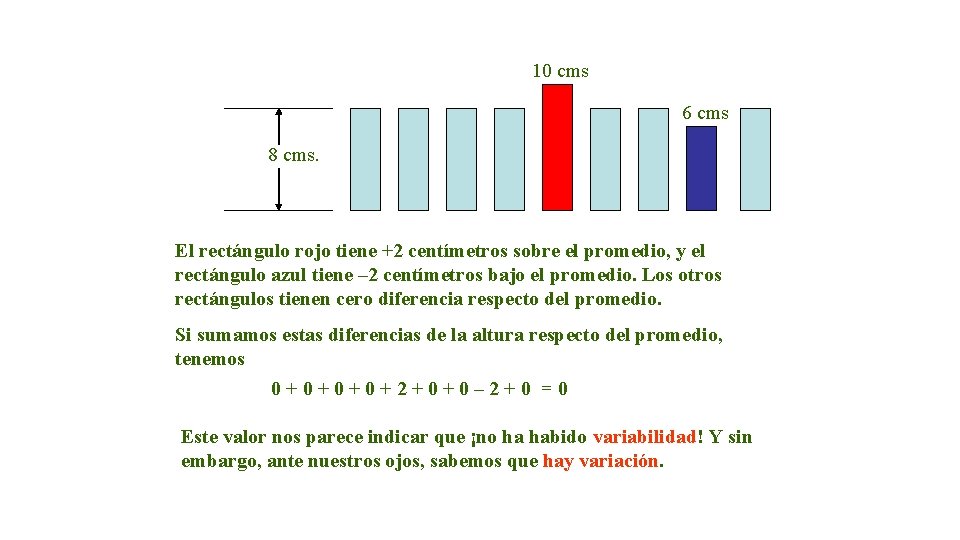
10 cms 6 cms 8 cms. El rectángulo rojo tiene +2 centímetros sobre el promedio, y el rectángulo azul tiene – 2 centímetros bajo el promedio. Los otros rectángulos tienen cero diferencia respecto del promedio. Si sumamos estas diferencias de la altura respecto del promedio, tenemos 0+0+2+0+0– 2+0 =0 Este valor nos parece indicar que ¡no ha habido variabilidad! Y sin embargo, ante nuestros ojos, sabemos que hay variación.

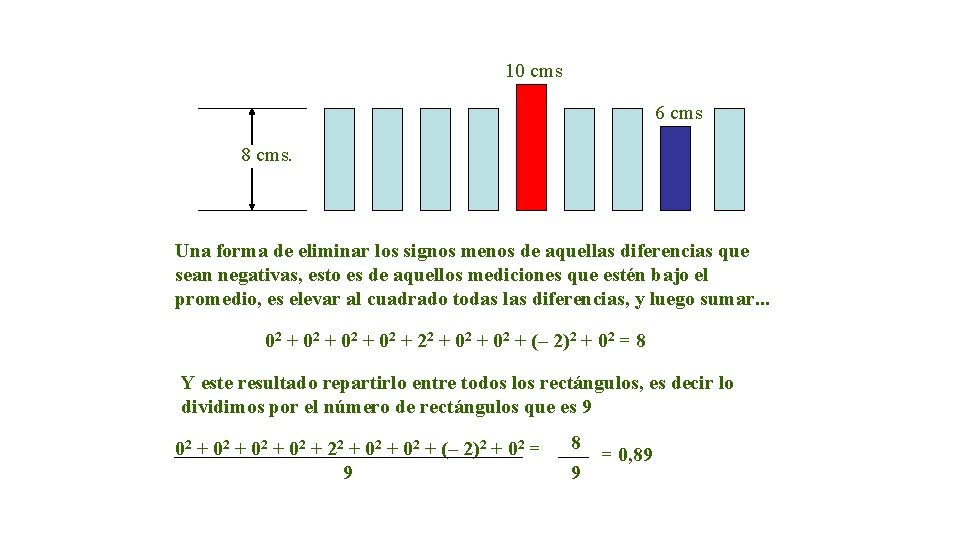
10 cms 6 cms 8 cms. Una forma de eliminar los signos menos de aquellas diferencias que sean negativas, esto es de aquellos mediciones que estén bajo el promedio, es elevar al cuadrado todas las diferencias, y luego sumar. . . 02 + 22 + 02 + (– 2)2 + 02 = 8 Y este resultado repartirlo entre todos los rectángulos, es decir lo dividimos por el número de rectángulos que es 9 02 + 22 + 02 + (– 2)2 + 02 = 9 8 9 = 0, 89

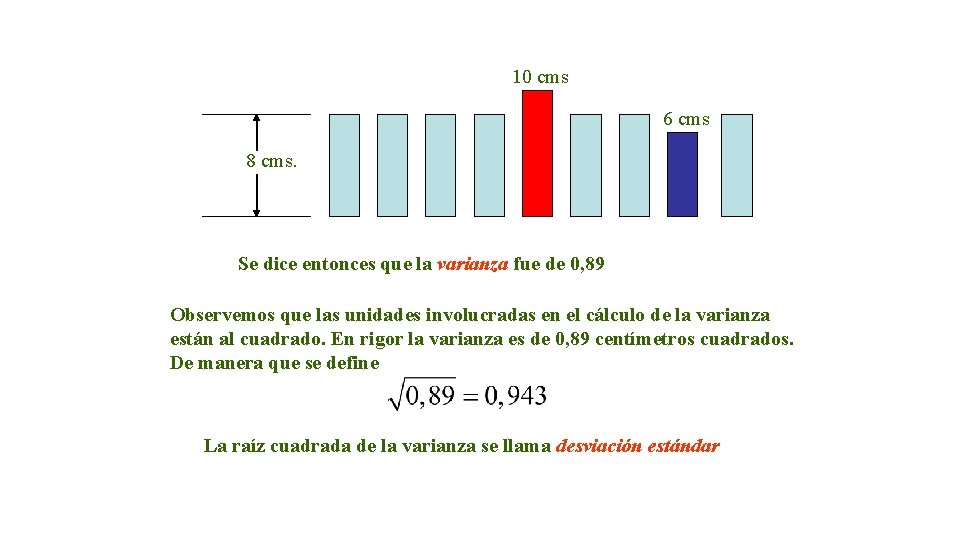
10 cms 6 cms 8 cms. Se dice entonces que la varianza fue de 0, 89 Observemos que las unidades involucradas en el cálculo de la varianza están al cuadrado. En rigor la varianza es de 0, 89 centímetros cuadrados. De manera que se define La raíz cuadrada de la varianza se llama desviación estándar

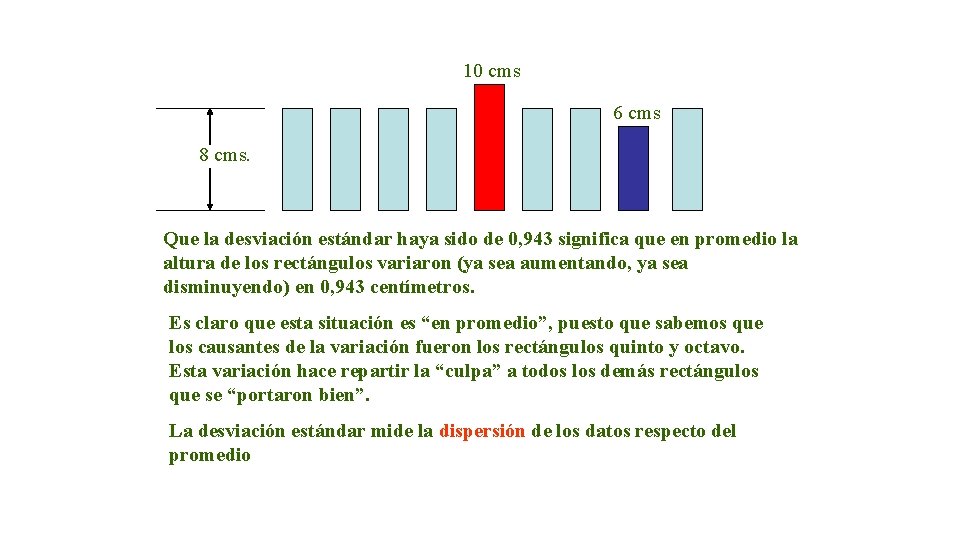
10 cms 6 cms 8 cms. Que la desviación estándar haya sido de 0, 943 significa que en promedio la altura de los rectángulos variaron (ya sea aumentando, ya sea disminuyendo) en 0, 943 centímetros. Es claro que esta situación es “en promedio”, puesto que sabemos que los causantes de la variación fueron los rectángulos quinto y octavo. Esta variación hace repartir la “culpa” a todos los demás rectángulos que se “portaron bien”. La desviación estándar mide la dispersión de los datos respecto del promedio

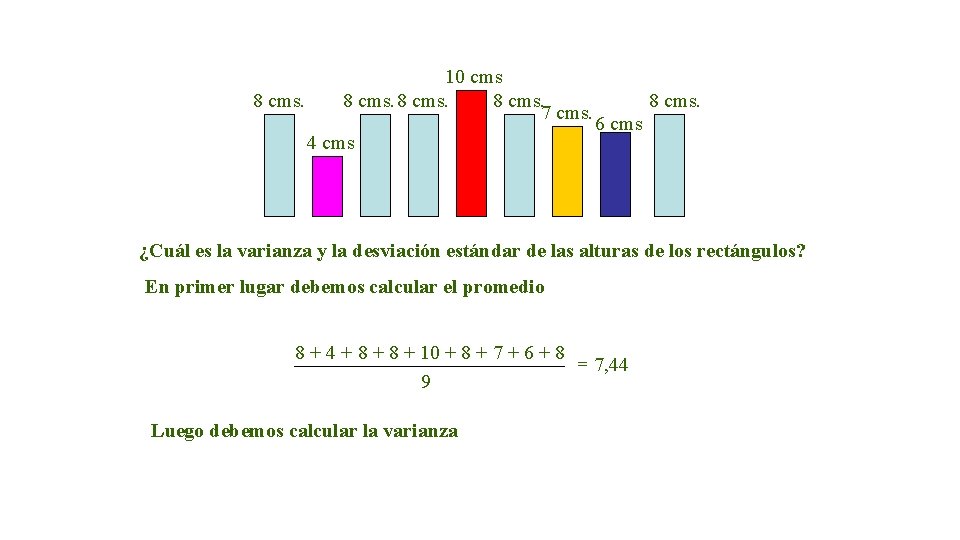
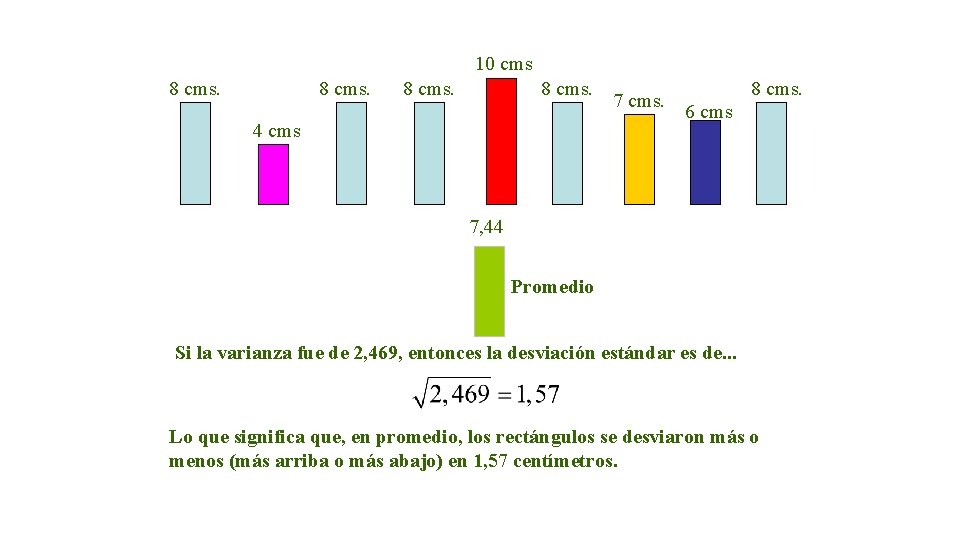
8 cms. 10 cms 8 cms. 7 cms. 4 cms 8 cms. 6 cms ¿Cuál es la varianza y la desviación estándar de las alturas de los rectángulos? En primer lugar debemos calcular el promedio 8 + 4 + 8 + 10 + 8 + 7 + 6 + 8 = 7, 44 9 Luego debemos calcular la varianza

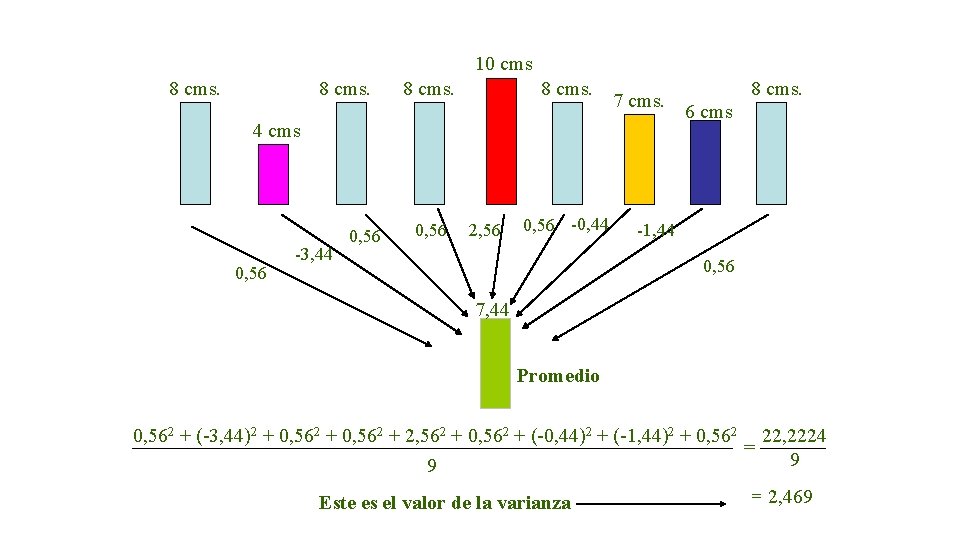
10 cms 8 cms. 7 cms. 4 cms 0, 56 -3, 44 0, 56 2, 56 0, 56 -0, 44 8 cms. 6 cms -1, 44 0, 56 7, 44 Promedio 0, 562 + (-3, 44)2 + 0, 562 + 2, 562 + 0, 562 + (-0, 44)2 + (-1, 44)2 + 0, 562 9 Este es el valor de la varianza = 22, 2224 9 = 2, 469

10 cms 8 cms. 4 cms 7 cms. 8 cms. 6 cms 7, 44 Promedio Si la varianza fue de 2, 469, entonces la desviación estándar es de. . . Lo que significa que, en promedio, los rectángulos se desviaron más o menos (más arriba o más abajo) en 1, 57 centímetros.

MEDIDAS DE DESVIACION PARA DATOS AGRUPADOS. LA DESVIACION ESTANDAR INDICA QUE TAN DISPERSOS ESTAN LOS DATOS CON RESPECTO A LA MEDIA.

PROPIEDADES DE LA VARIANZA Y LA DESVIACION ESTANDAR.

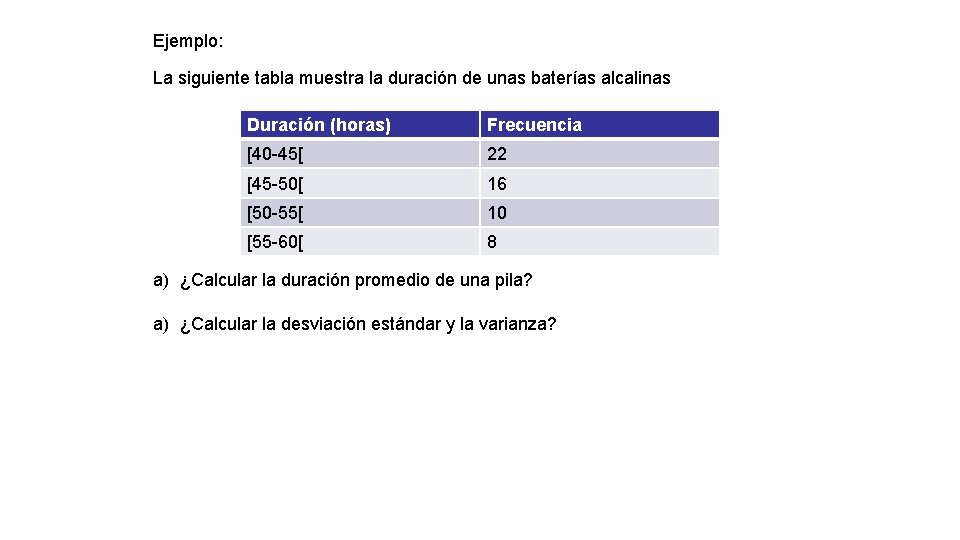
Ejemplo: La siguiente tabla muestra la duración de unas baterías alcalinas Duración (horas) Frecuencia [40 -45[ 22 [45 -50[ 16 [50 -55[ 10 [55 -60[ 8 a) ¿Calcular la duración promedio de una pila? a) ¿Calcular la desviación estándar y la varianza?

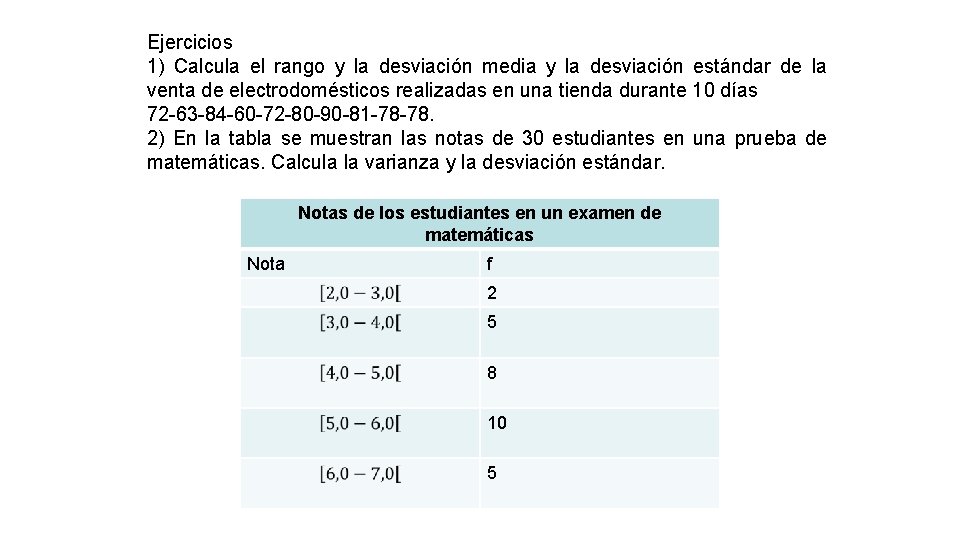
Ejercicios 1) Calcula el rango y la desviación media y la desviación estándar de la venta de electrodomésticos realizadas en una tienda durante 10 días 72 -63 -84 -60 -72 -80 -90 -81 -78 -78. 2) En la tabla se muestran las notas de 30 estudiantes en una prueba de matemáticas. Calcula la varianza y la desviación estándar. Notas de los estudiantes en un examen de matemáticas Nota f 2 5 8 10 5

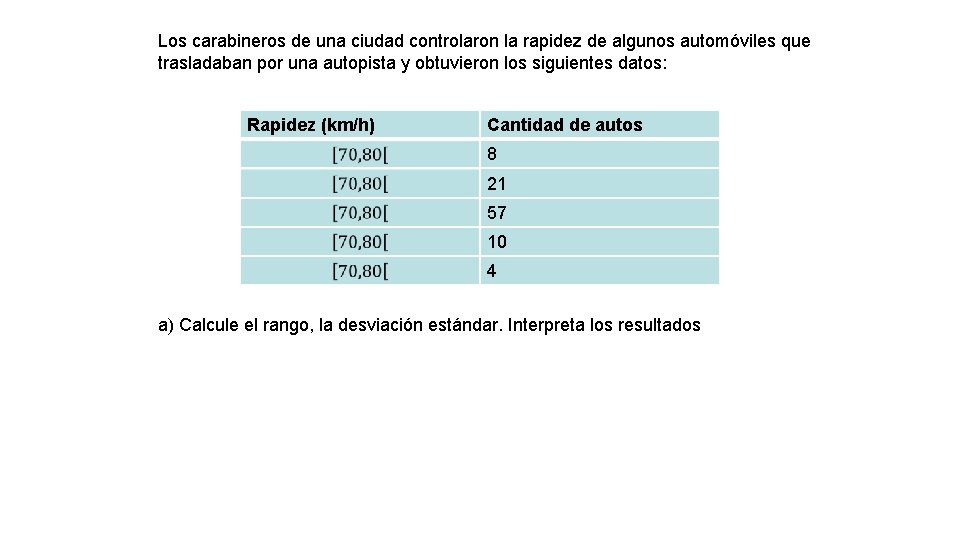
Los carabineros de una ciudad controlaron la rapidez de algunos automóviles que trasladaban por una autopista y obtuvieron los siguientes datos: Rapidez (km/h) Cantidad de autos 8 21 57 10 4 a) Calcule el rango, la desviación estándar. Interpreta los resultados

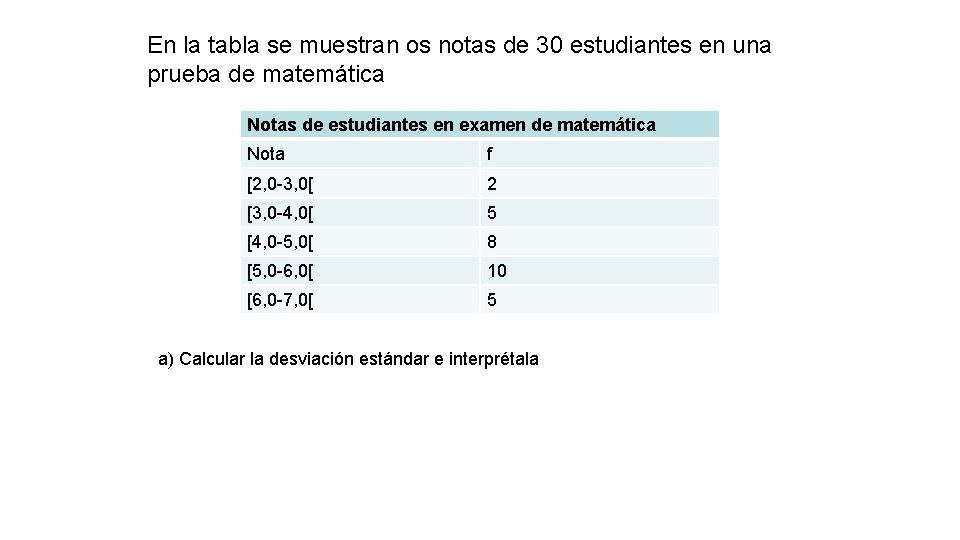
En la tabla se muestran os notas de 30 estudiantes en una prueba de matemática Notas de estudiantes en examen de matemática Nota f [2, 0 -3, 0[ 2 [3, 0 -4, 0[ 5 [4, 0 -5, 0[ 8 [5, 0 -6, 0[ 10 [6, 0 -7, 0[ 5 a) Calcular la desviación estándar e interprétala

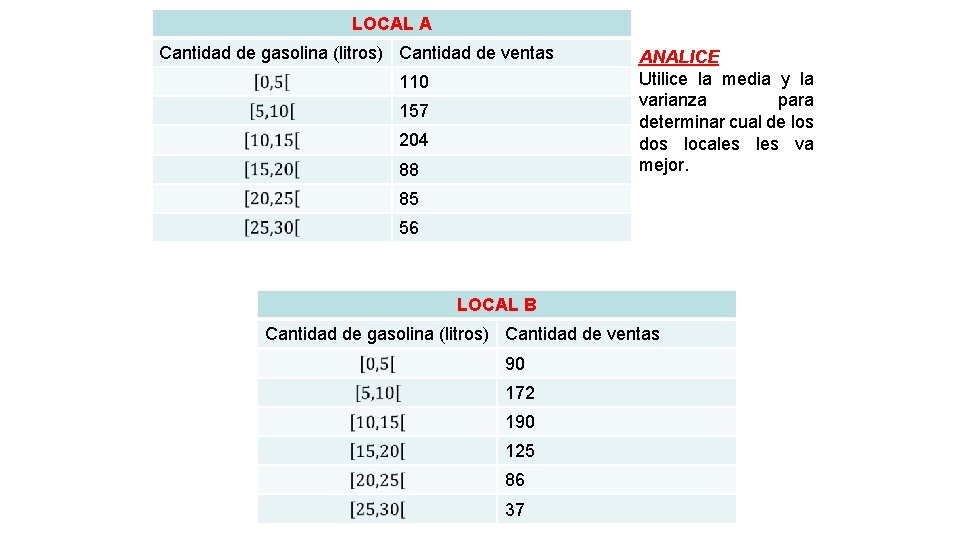
COMPARACION DE MUESTRAS Cuando se tienen dos o mas muestras, se pueden comparar sus características utilizando las medias de tendencia central de posición y las de dispersión, y a partir de ellas obtener conclusiones. Nota: Nos es necesario que las muestras sean del mismo tamaño. Ejemplo Una estación de bencina reporto las siguientes distribuciones de frecuencia, la que relaciona la cantidad de litros de bencina vendidas aun grupo de clientes en un día lunes en dos locales diferentes.

LOCAL A Cantidad de gasolina (litros) Cantidad de ventas 110 157 204 88 ANALICE Utilice la media y la varianza para determinar cual de los dos locales va mejor. 85 56 LOCAL B Cantidad de gasolina (litros) Cantidad de ventas 90 172 190 125 86 37