MEDICAL IMAGING INFORMATICS Lecture 1 Basics of Medical

MEDICAL IMAGING INFORMATICS: Lecture # 1 Basics of Medical Imaging Informatics: Estimation Theory Norbert Schuff Professor of Radiology VA Medical Center and UCSF Norbert. schuff@ucsf. edu Medical Imaging Informatics 2009, Nschuff Course # 170. 03 Slide 1/31 UCSF VA Department of Radiology & Biomedical Imaging

What Is Medical Imaging Informatics? • • • • • • Picture Archiving and Communication System (PACS) Imaging Informatics for the Enterprise Image-Enabled Electronic Medical Records Radiology Information Systems (RIS) and Hospital Information Systems (HIS) Digital Image Acquisition Image Processing and Enhancement Image Data Compression 3 D, Visualization and Multi-media Speech Recognition Computer-Aided Detection and Diagnosis (CAD). Imaging Facilities Design Imaging Vocabularies and Ontologies Data-mining from medical image databases Transforming the Radiological Interpretation Process (TRIP)[2] DICOM, HL 7 and other Standards Workflow and Process Modeling and Simulation Quality Assurance Archive Integrity and Security Teleradiology Radiology Informatics Education Etc. Medical Imaging Informatics 2009, Nschuff Course # 170. 03 Slide 2/31 UCSF VA Department of Radiology & Biomedical Imaging
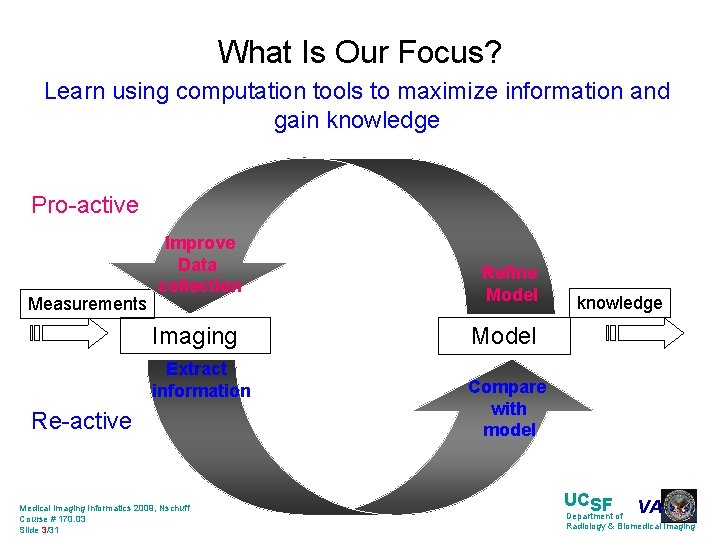
What Is Our Focus? Learn using computation tools to maximize information and gain knowledge Pro-active Measurements Improve Data collection Refine Model Imaging Model Extract information Re-active Medical Imaging Informatics 2009, Nschuff Course # 170. 03 Slide 3/31 knowledge Compare with model UCSF VA Department of Radiology & Biomedical Imaging

Challenge: Extract Maximum Information 1. Q: How can we estimate quantities of interest from a given set of uncertain (noise) measurements? A: Apply estimation theory (1 st lecture by Norbert) 2. Q: How can we code the quantities? A: Apply information theory (2 nd lecture by Wang) Medical Imaging Informatics 2009, Nschuff Course # 170. 03 Slide 4/31 UCSF VA Department of Radiology & Biomedical Imaging
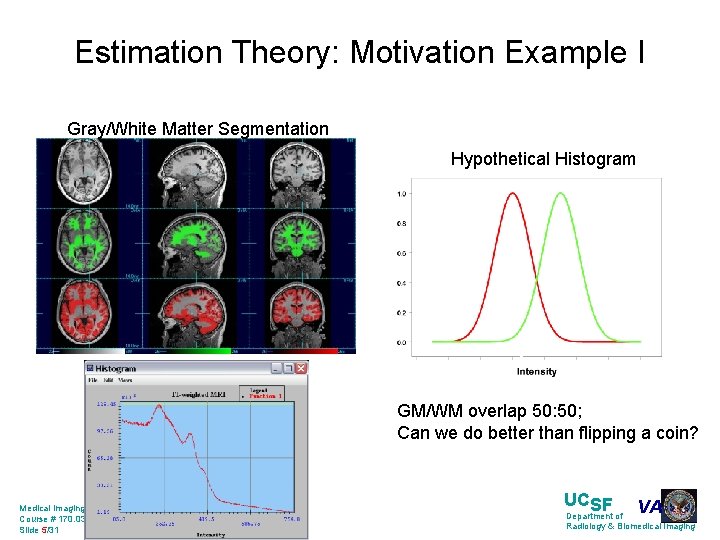
Estimation Theory: Motivation Example I Gray/White Matter Segmentation Hypothetical Histogram GM/WM overlap 50: 50; Can we do better than flipping a coin? Medical Imaging Informatics 2009, Nschuff Course # 170. 03 Slide 5/31 UCSF VA Department of Radiology & Biomedical Imaging
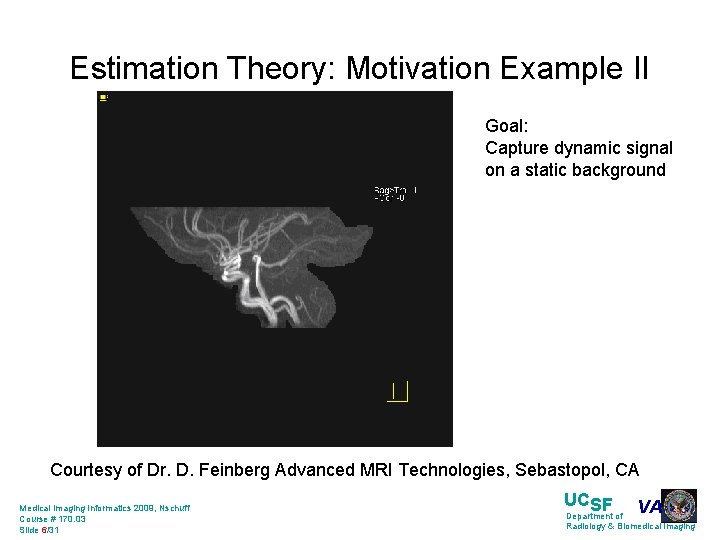
Estimation Theory: Motivation Example II Goal: Capture dynamic signal on a static background Courtesy of Dr. D. Feinberg Advanced MRI Technologies, Sebastopol, CA Medical Imaging Informatics 2009, Nschuff Course # 170. 03 Slide 6/31 UCSF VA Department of Radiology & Biomedical Imaging

Basic Concepts Suppose we have N scalar measurements : We want to determine M quantities (parameters): Definition: An estimator is: Error estimator: Medical Imaging Informatics 2009, Nschuff Course # 170. 03 Slide 7/31 UCSF VA Department of Radiology & Biomedical Imaging
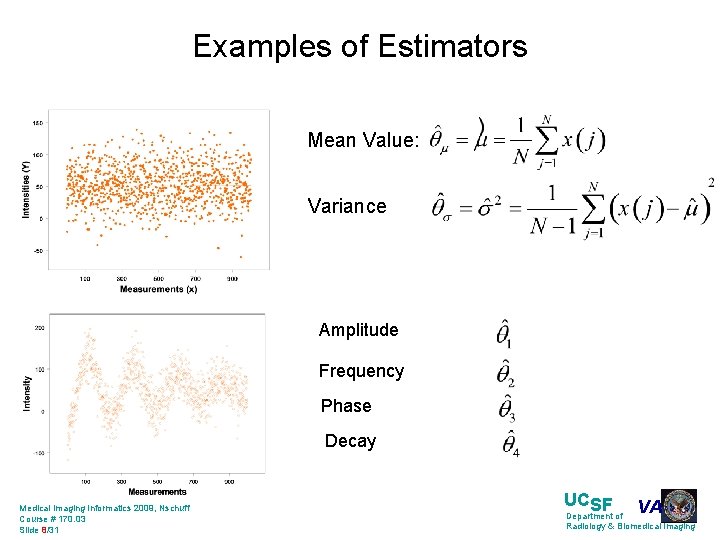
Examples of Estimators Mean Value: Variance Amplitude: Frequency: Phase: Decay: Medical Imaging Informatics 2009, Nschuff Course # 170. 03 Slide 8/31 UCSF VA Department of Radiology & Biomedical Imaging

Some Desirable Properties of Estimators I: Unbiased: Mean value of the error should be zero Consistent: Error estimator should decrease asymptotically as number of measurements increase. (Mean Square Error (MSE)) If estimator is biased Medical Imaging Informatics 2009, Nschuff Course # 170. 03 Slide 9/31 variance bias UCSF VA Department of Radiology & Biomedical Imaging

Some Desirable Properties of Estimators II: Efficient: Co-variance matrix of error should decrease asymptotically to its minimal value, i. e. inverse of Fisher’s information matrix) for large N Medical Imaging Informatics 2009, Nschuff Course # 170. 03 Slide 10/31 UCSF VA Department of Radiology & Biomedical Imaging

Example: Properties Of Estimators Mean and Variance Mean: The sample mean is an unbiased estimator of the true mean Variance: The variance is a consistent estimator because It approaches zero for large number of measurements. Medical Imaging Informatics 2009, Nschuff Course # 170. 03 Slide 11/31 UCSF VA Department of Radiology & Biomedical Imaging

Least-Squares Estimation Linear Model: where N > M Generally: Medical Imaging Informatics 2009, Nschuff Course # 170. 03 Slide 12/31 UCSF VA Department of Radiology & Biomedical Imaging

Least-Squares Estimation The best what we can do: Minimizing ELSE with regard to leads to • LSE is popular choice for model fitting • Useful for obtaining a descriptive measure But • Makes no assumptions about distributions of data or parameters • Has no basis for statistics Medical Imaging Informatics 2009, Nschuff Course # 170. 03 Slide 13/31 UCSF VA Department of Radiology & Biomedical Imaging

Maximum Likelihood (ML) Estimator We have: Xn is random sample from a pool with certain probability distribution. Goal: Find that gives the most likely probability distribution underlying x. N. Max likelihood function ML can be found by Medical Imaging Informatics 2009, Nschuff Course # 170. 03 Slide 14/31 UCSF VA Department of Radiology & Biomedical Imaging

Example I: ML of Normal Distribution ML function of a normal distribution log ML function 1 st log ML equation MLE of the mean 2 nd log ML equation MLE of the variance Medical Imaging Informatics 2009, Nschuff Course # 170. 03 Slide 15/31 UCSF VA Department of Radiology & Biomedical Imaging

Example II: Binominal Distribution (Coin Toss) Probability density function: n= number of tosses w= probability of success f(y|n=10, w) Medical Imaging Informatics 2009, Nschuff Course # 170. 03 Slide 16/31 y UCSF VA Department of Radiology & Biomedical Imaging

Likelihood Function Of Coin Tosses Given the observed data f (y|w=0. 7, n=10) (and model), find the parameter w that most likely produced the data. Medical Imaging Informatics 2009, Nschuff Course # 170. 03 Slide 17/31 UCSF VA Department of Radiology & Biomedical Imaging

ML Estimation Of Coin Toss Compute log likelihood function Evaluate ML equation According to the MLE principle, the PDF f(y|w=y/n) for a given n is the distribution that is most likely to have generated the observed data of y. Medical Imaging Informatics 2009, Nschuff Course # 170. 03 Slide 18/31 UCSF VA Department of Radiology & Biomedical Imaging

Connection between ML and LSE Assume: are independent of v. N ML and v. N have the same distribution v. N is zero mean and gaussian ML function of a normal distribution Clearly, p(x| ) is maximized when LSE is minimized Medical Imaging Informatics 2009, Nschuff Course # 170. 03 Slide 19/31 UCSF VA Department of Radiology & Biomedical Imaging

Properties Of The ML Estimator • is consistent: the MLE recovers asymptotically the true parameter values that generated the data for N inf; • Is efficient: The MLE achieves asymptotically the minimum error (= max. information) Medical Imaging Informatics 2009, Nschuff Course # 170. 03 Slide 20/31 UCSF VA Department of Radiology & Biomedical Imaging

Maximum A-Posteriori (MAP) Estimator We have random sample: We also have random parameters: Goal: Find the most likely (max. posterior density of ) given x. N. Maximize joint density MAO can be found by Medical Imaging Informatics 2009, Nschuff Course # 170. 03 Slide 21/31 UCSF VA Department of Radiology & Biomedical Imaging

MAP Of Normal Distribution We have random sample: The sample mean of MAP is: If we do not have prior information on , inf or T inf Medical Imaging Informatics 2009, Nschuff Course # 170. 03 Slide 22/31 UCSF VA Department of Radiology & Biomedical Imaging
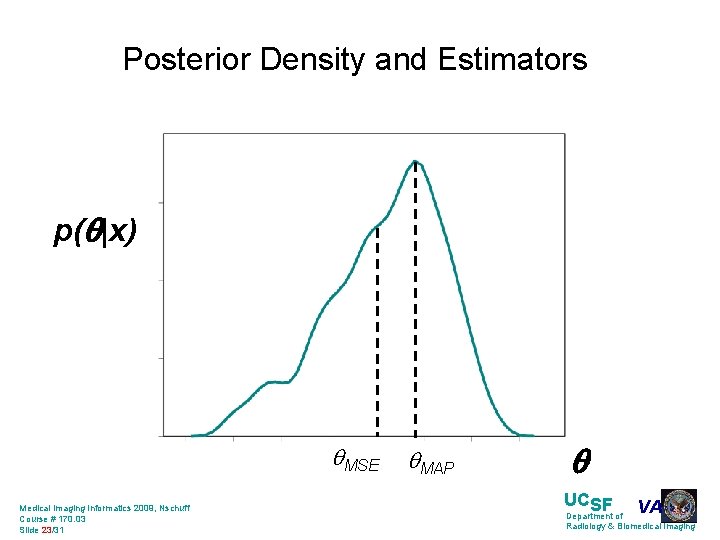
Posterior Density and Estimators p( |x) MSE Medical Imaging Informatics 2009, Nschuff Course # 170. 03 Slide 23/31 MAP UCSF VA Department of Radiology & Biomedical Imaging

Summary • LSE is a descriptive method to accurately fit data to a model. • MLE is a method to seek the probability distribution that makes the observed data most likely. • MAP is a method to seek the most probably parameter value given prior information about the parameters and the observed data. • If the influence of prior information decreases, i. e. many measurements, MAP approaches MLE Medical Imaging Informatics 2009, Nschuff Course # 170. 03 Slide 24/31 UCSF VA Department of Radiology & Biomedical Imaging

Some Priors in Imaging • • • Smoothness of the brain Anatomical boundaries Intensity distributions Anatomical shapes Physical models – Point spread function – Bandwidth limits • Etc. Medical Imaging Informatics 2009, Nschuff Course # 170. 03 Slide 25/31 UCSF VA Department of Radiology & Biomedical Imaging

Imaging Software Using MLE And MAP Medical Imaging Informatics 2009, Nschuff Course # 170. 03 Slide 26/31 UCSF VA Department of Radiology & Biomedical Imaging

Segmentation Using MLE A: Raw MRI B: SPM 2 C: EMS D: HBSA from Habib Zaidi, et al, Neuro. Image 32 (2006) 1591 – 1607 Medical Imaging Informatics 2009, Nschuff Course # 170. 03 Slide 27/31 UCSF VA Department of Radiology & Biomedical Imaging
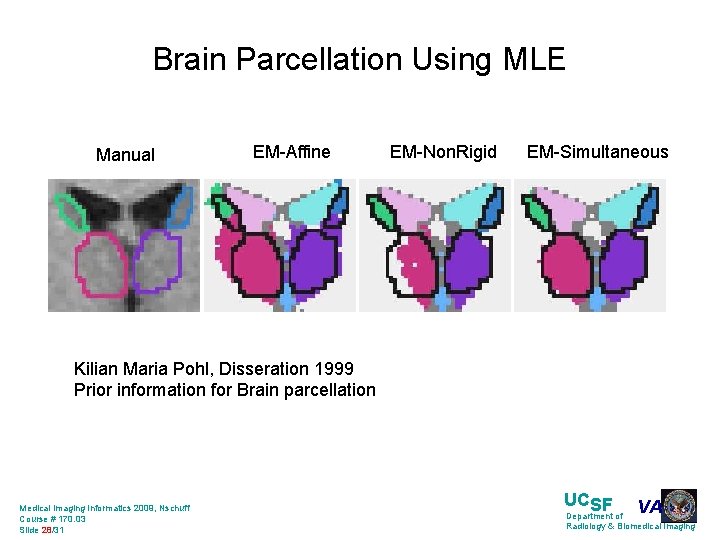
Brain Parcellation Using MLE Manual EM-Affine EM-Non. Rigid EM-Simultaneous Kilian Maria Pohl, Disseration 1999 Prior information for Brain parcellation Medical Imaging Informatics 2009, Nschuff Course # 170. 03 Slide 28/31 UCSF VA Department of Radiology & Biomedical Imaging
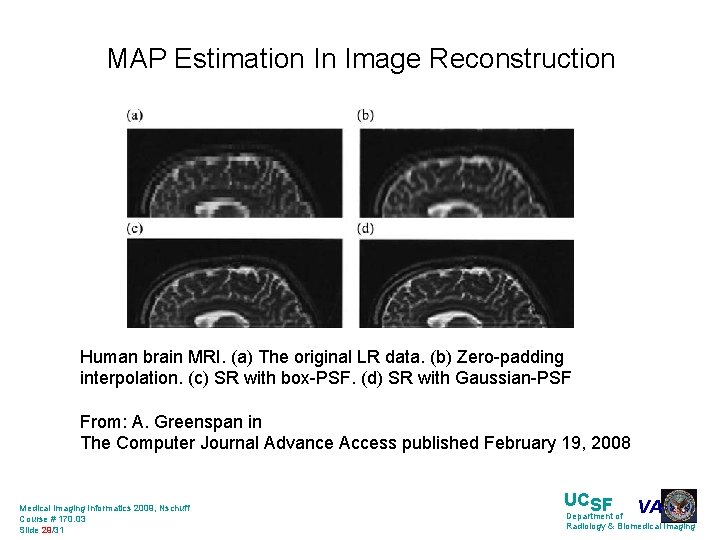
MAP Estimation In Image Reconstruction Human brain MRI. (a) The original LR data. (b) Zero-padding interpolation. (c) SR with box-PSF. (d) SR with Gaussian-PSF. From: A. Greenspan in The Computer Journal Advance Access published February 19, 2008 Medical Imaging Informatics 2009, Nschuff Course # 170. 03 Slide 29/31 UCSF VA Department of Radiology & Biomedical Imaging

Literature Mathematical • H. Sorenson. Parameter Estimation – Principles and Problems. Marcel Dekker (pub)1980. Signal Processing • S. Kay. Fundamentals of Signal Processing – Estimation Theory. Prentice Hall 1993. • L. Scharf. Statistical Signal Processing: Detection, Estimation, and Time Series Analysis. Addison-Wesley 1991. Statistics: • A. Hyvarinen. Independent Component Analysis. John Wileys & Sons. 2001. • New Directions in Statistical Signal Processing. From Systems to Brain. Ed. S. Haykin. MIT Press 2007. Medical Imaging Informatics 2009, Nschuff Course # 170. 03 Slide 30/31 UCSF VA Department of Radiology & Biomedical Imaging
- Slides: 30