Mecnica vectorial para ingeniera Capitulo 1 Capitulo 2

Mecánica vectorial para ingeniería Capitulo 1 Capitulo 2 Vargas Barrera Ramón Yael S

Capitulo 1: introducción S ¿Qué es la mecánica? S La mecánica es la ciencia que describe y predice las condiciones de reposo o movimiento de los cuerpos bajo la acción de fuerzas. Se divide en tres partes : S Mecánica cuerpo rígido: estática y dinámica S Mecánica de cuerpos deformables: estudia la deformaciones S Mecánica de fluidos: fluidos compresibles y fluidos incompresibles

Capitulo 1 S Conceptos y principios fundamentales S Conceptos básicos: S Espacio: posición de un punto S Masa: comparar los cuerpos con base en ciertos experimentos mecánicos fundamentales. S Fuerza : acción de un cuerpo sobre otro.

Capitulo 1 S Vector : ente matemático que consta de magnitud, sentido y dirección. S Ley del paralelogramo para adición de fuerzas: dos fuerzas que actúan sobre una partícula puede sustituirse por una sola fuerza llamada resultante, que se obtiene al trazarla diagonal del paralelogramo que tiene los lados iguales a las fuerzas dadas.

Capitulo 1 Principio de transmisibilidad S establece que las condiciones de equilibrio o movimiento de un sólido rígido permanecerán inalterables si una fuerza F, ejercida sobre un punto dado, se reemplaza por otra fuerza F’ de igual magnitud, dirección y sentido, que actúa sobre un punto diferente, siempre que las fuerzas tengan la misma línea de acción

Capitulo 1 Tres leyes fundamentales de newton S Primera: un objeto permanece en reposo hasta que se le aplique una fuerza. S Segunda: F=ma S Tercera: toda fuerza le corresponde una reaccion de igual magnitud y dirección pero diferente sentido

Capitulo 1 Sistema de unidades SI Sistema Ingles g slug m ft N lb

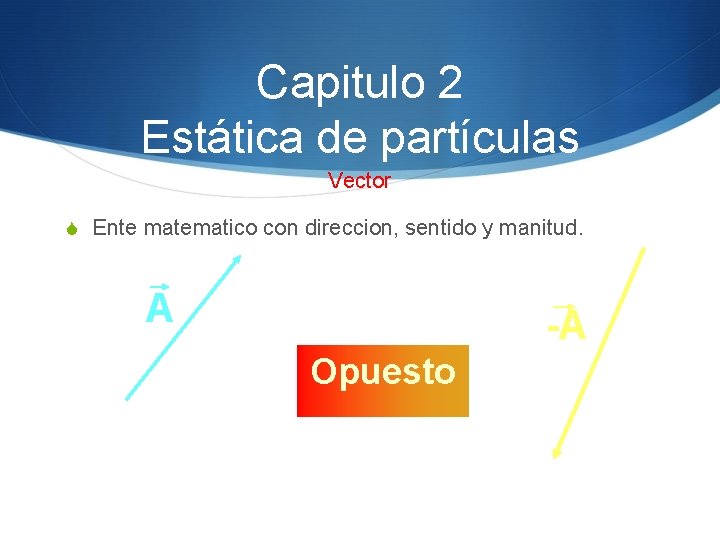
Capitulo 2 Estática de partículas Vector S Ente matematico con direccion, sentido y manitud. A -A Opuesto

Capitulo 2 Vectores Nulo 0 = A + ( -A )

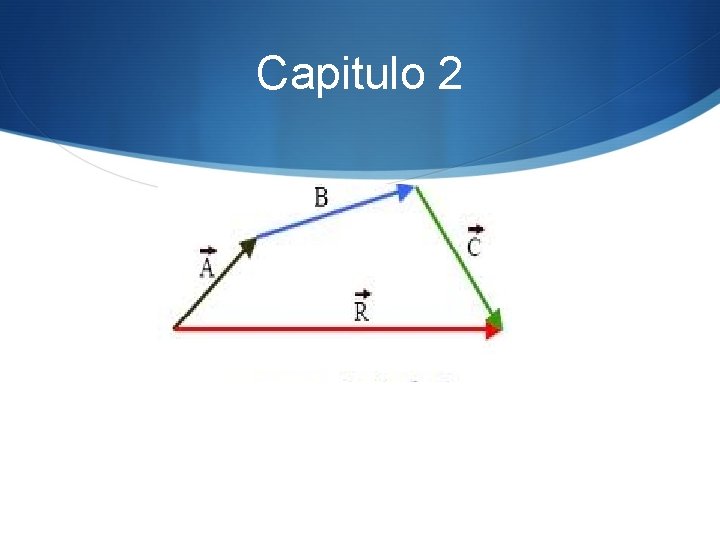
Capitulo 2 Suma de vectores Puesto que el paralelogramo construido con los vectores P y Q se seleccionen, se concluye que la adición de los vectores conmitativa y se escribe: P+Q=Q+P A partir de la ley del paralelogramo se puede obtener otro metodo. Este metodo llamado regla del triangulo

Capitulo 2 Los pasos a dar para obtener el vector suma son: S 1. Tomar un representante de uno de ellos ( a→ por ejemplo) que tenga por origen el extremo del otro ( b → en este caso). S 2. Formar el vector suma uniendo el origen del primero con el extremo del segundo. S Este procedimiento empleado para obtener la suma se denomina "REGLA DEL TRIÁNGULO"

Capitulo 2 Resta de un vector Se define como la adicion del vector negativo correspondiente. De manera que el vector V-W que representa la diferencia de los vectore V y W se obtiene agregandole a V el vector negativo –W. Se ecribe: V-W=V+(-W)

Capitulo 2 Método del polígono Este método es simplemente la extensión del método del triángulo. Es decir, se van desplazando los vectores para colocarlos la "cabeza" del uno con la cola del otro y la resultante final es el vector que cierra el polígono desde la "cola" quedo libre hasta la "cabeza" quedo también libre. Nuevamente el orden en que se realice la suma no interesa, pues aunque el polígno resultante tiene forma diferente en cada caso, la resultante final conserva su magnitud, su dirección y su sentido.

Capitulo 2

Capitulo 2 Producto de un escalar y un vector Se define el rpoducto k. P de un escalar k y un vector P como un vector que tiene la misma dirección y sentido que P (si k es positivo), o la misma dirección pero sentido opuesto a P(si k es negativo) y una magnitud igual al producto de P y el valor absoluto de k.

Capitulo 2 Descomposición de una fuerza en sus componentes Una sola fuerza F que actua sobre una particula puede reempazarse por dos o más fuerzas que produscan el mismo efecto sobre la particula , a estas fuerzas se le llaman componentes. El nuemro de formas en que la fuerza F se puede descomponerse en sus componentes es ilimitado. Dos casos son especiales: 1. Una de las componentes P se conoce. La segunada componente de Q se obtiene aplicando la regla del triangulo y uniendo la punta de P a la punta de F 2. Se conoce la linea de acción de cada una de las componentes. La magnitud y el sentido de las componentes se obtiene al aplicar la ley del palalelogramo y tarzando lineas.

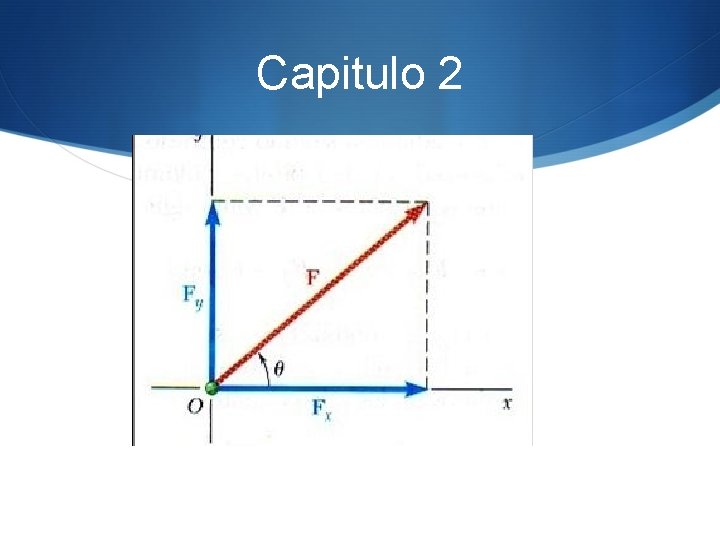
Componentes rectangulares de una fuerza. Vectores unitarios En muchos problemas será conveniente descomponer una fuerza en sus componentes perpendiculares entre sí. En la figura 2. 18, la fuerza F se ha descompuesto en una componente Fx a lo largo del eje x y una componente Fy a lo largo del eje y. El paralelogramo trazado para obtener las dos componentes es un rectangulo, y las fuerzas Fx y Fy se llaman componentes rectangulares.

Capitulo 2

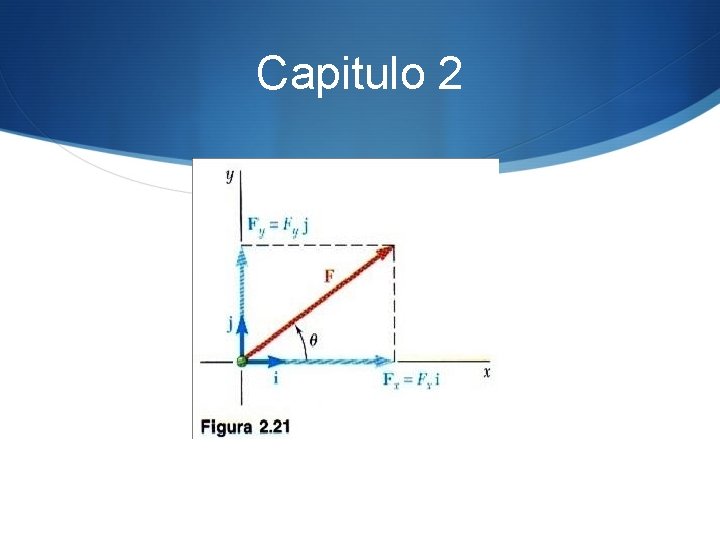
Capitulo 2 S E n este punto se introducirán dos vectores de magnitud unitaria dirigidos a lo largo de los ejes positivos x y y. A estos vectores se les llama vectores unitarios y se representan por i y j, respectivamente. Se observa que las componentes rectangulares Fx y Fy de una fuerza F pueden obtenerse con la multiplicación de sus respectivos vectores unitarios i y j por escalares apropiados (figura 2. 21). Se escribe S Fx = Fxi ------ Fy = Fy j S F = Fxi + Fyj

Capitulo 2

Capitulo 2 S Entonces se representa: