Mecnica dos Fluidos Dinmica dos Fluidos Programa da

Mecânica dos Fluidos Dinâmica dos Fluidos

Programa da aula ◦ ◦ Conservação de Massa (Continuidade) Equação da Conservação da Energia Equação de Bernoulli Exercícios.

Mecânica dos Fluidos Conservação de massa (Equação da Continuidade)

Equação da Continuidade • É a equação que mostra a conservação da massa de líquido no conduto, ao longo de todo o escoamento; • Pela condição de escoamento em regime permanente, podemos afirmar que entre as seções (1) e (2), não ocorre nem acúmulo, nem falta de massa: m 1 = m 2 = m = cte

Equação da Continuidade ρ = Δm/V Δm=ρ. V V = A. Δl Qm= Δm/Δt = ρ. V/ Δt = ρ. A. Δl /Δt = ρ. A. v

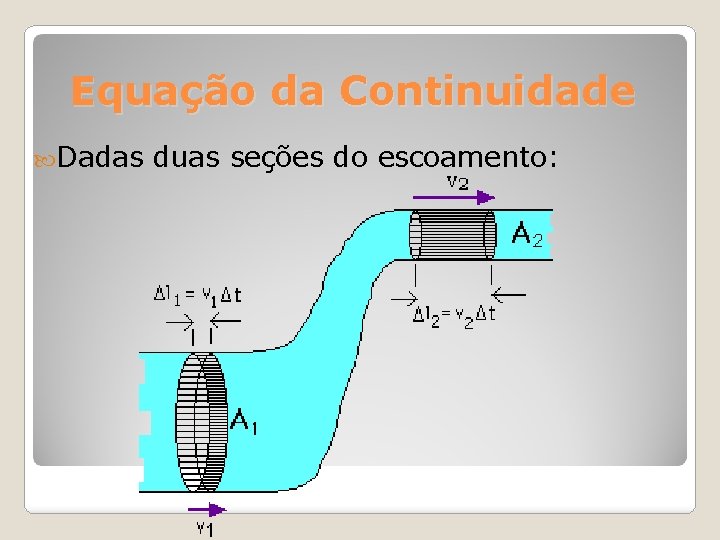
Equação da Continuidade Dadas duas seções do escoamento:

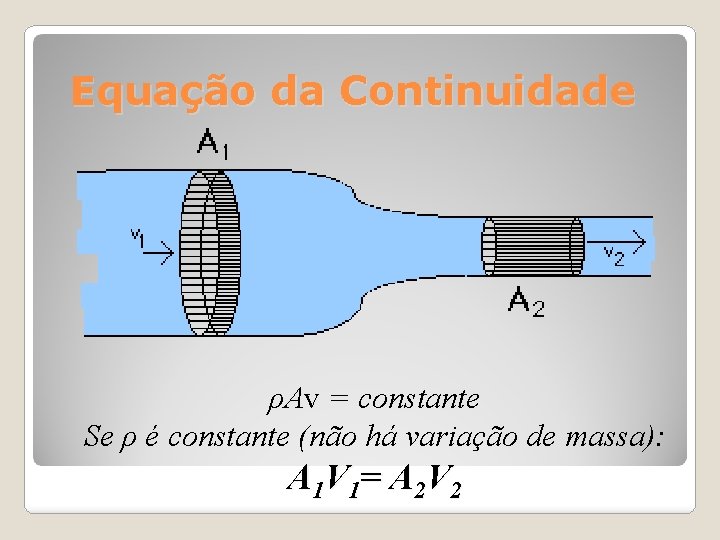
Equação da Continuidade ρAv = constante Se ρ é constante (não há variação de massa): A 1 V 1= A 2 V 2

Equação da Continuidade A equação da continuidade estabelece que: • o volume total de um fluido incompressível (fluido que mantém constante a densidade apesar das variações na pressão e na temperatura) que entra em um tubo será igual aquele que está saindo do tubo; • a vazão medida num ponto ao longo do tubo será igual a vazão num outro ponto ao longo do tubo, apesar da área da seção transversal do tubo em cada ponto ser diferente. Q = A 1 v 1 = A 2 v 2 = constante

Equação da Continuidade Isto equivale a dizer que: • No escoamento de fluidos incompressíveis em regime permanente, a vazão em volume, ou simplesmente a vazão, que passa através de qualquer seção do tubo de corrente é constante. • De forma genérica: Q = A 1 v 1 = A 2 v 2 = constante Q=A. V, onde: V=velocidade média

Problema Resolvido 1 Uma mangueira de diâmetro de 2 cm é usada para encher um balde de 20 litros. a)Se leva 1 minuto para encher o balde. Qual é a velocidade com que a água passa pela mangueira? b)Um brincalhão aperta a saída da mangueira até ela ficar com um diâmetro de 5 mm, e acerta o vizinho com água. Qual é a velocidade com que a água sai da mangueira?

Problema Resolvido 1 Solução: a) A área da seção transversal da mangueira será dada por A 1 = πr 2 = π(2 cm /2)2 = π cm 2. Para encontrar a velocidade, v 1 , usamos Taxa de escoamento (vazão)= A 1 v 1 = 20 L / min = 20 x 103 cm 3 / 60 s v 1= (20 x 103 cm 3 / 60 s) / (π cm 2) = 106, 1 cm/s. b) A taxa de escoamento ( A 1 v 1 ) da água que se aproxima da abertura da mangueira deve ser igual a taxa de escoamento que deixa a mangueira ( A 2 v 2 ). Isto resulta em: v 2= A 1 v 1 / A 2 = (π. 106, 1) / (π. (0, 5/2)2) = 1698 cm/s.

Problema Resolvido 2 Num sistema de drenagem, um tubo de 25 cm de diâmetro interno drena para outro tubo conectada de 22 cm de diâmetro interno. Se a velocidade da água através do tubo maior é 5 cm/s, determine a velocidade média no tubo menor.

Problema Resolvido 2 SOLUÇÃO Usando a equação da continuidade, temos A 1 v 1 = A 2 v 2 π(12, 5 cm)2 (5 cm/s) = π(11, 0 cm)2 (v 2) Resolvendo para v 2: v 2 = 6, 42 cm/s.

Problema Resolvido 3 Assumindo o fluxo de um fluido incompressível como o sangue, se a velocidade medida num ponto dentro de um vaso sanguíneo é 40 cm/s, qual é a velocidade num segundo ponto que tem um terço do raio original?

Problema Resolvido 3 Este problema pode ser resolvido usando a equação da continuidade: ρ1 A 1 v 1= ρ2 A 2 v 2 onde: ρ é a densidade do sangue A é a área da seção transversal v é a velocidade e os subscritos 1 e 2 referem-se às localizações dentro do vaso. Desde que o fluxo sangüíneo é incompressível, temos ρ1= ρ2 v 1 = 40 cm/s A 1=πr 12 A 2 = πr 22 r 2=r 1/3, A 2= π(r 1/3)2 = (π r 12)/9 ou A 2=A 1/9 A 1/A 2 = 9 Resolvendo: v 2 = (A 1 v 1)/A 2 = 9 v 1 = 9 x 40 cm/s = 360 cm/s

Mecânica dos Fluidos Equação de Bernoulli para fluidos ideais

O que são “Fluidos Ideais”? Por definição: “Escoamento ideal ou escoamento sem atrito, é aquele no qual não existem tensões de cisalhamento atuando no movimento do fluido”.

O que são “Fluidos Ideais”? De acordo com a lei de Newton, para um fluido em movimento esta condição é obtida - Quando a viscosidade do fluido é nula (ou desprezível): ou µ=0 -Quando os componentes da velocidade do escoamento não mais exibem variações de grandeza na direção perpendicular ao componente da velocidade considerada: =0

Condições Ideais de Escoamento Um fluido que quando em escoamento satisfaz as condições acima, é chamado de fluido ideal

Fluidos Incompressíveis � Compressíveis: ρ→ varia � Incompressíveis: ρ→ é constante

Relembrando. . . Classificação do Escoamento Quanto à variação no tempo: ◦ Permanente: quando as propriedades em uma dada seção do escoamento não se alteram com o decorrer do tempo. Linhas de corrente, trajetórias e linhas de emissão coincidem; ◦ Não Permanente: quando as propriedades do fluido mudam no decorrer do escoamento;

Equação da Continuidade É a equação que mostra a conservação da massa de líquido no conduto, ao longo de todo o escoamento; Pela condição de escoamento em regime permanente, podemos afirmar que entre as seções (1) e (2), não ocorre nem acúmulo, nem falta de massa: m 1 = m 2 = m = cte

Equação de Bernoulli A equação de Bernoulli é um caso particular da equação da energia aplicada ao escoamento, onde adotam-se as seguintes hipóteses:

Equação de Bernoulli Escoamento em regime permanente Escoamento incompressível Escoamento de um fluido considerado ideal, ou seja, aquele onde a viscosidade é considerada nula, ou aquele que não apresenta dissipação de energia ao longo do escoamento Escoamento apresentando distribuição uniforme das propriedades nas seções Escoamento sem presença de máquina hidráulica, ou seja, sem a presença de um dispositivo que forneça, ou retira energia do fluido Escoamento sem troca de calor

Equação de Bernoulli A energia presente em um fluido em escoamento sem troca de calor pode ser separada em três parcelas: ◦ Energia de pressão (piezocarga); ◦ Energia cinética (taquicarga); ◦ Energia de posição (hipsocarga);

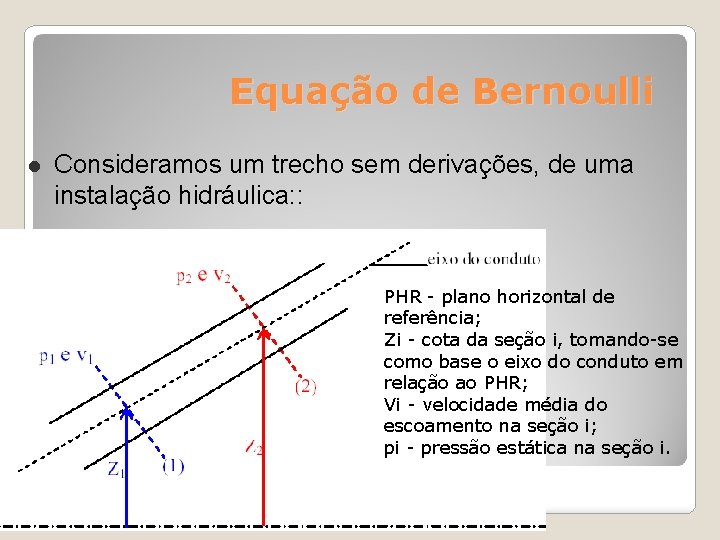
Equação de Bernoulli Consideramos um trecho sem derivações, de uma instalação hidráulica: : PHR - plano horizontal de referência; Zi - cota da seção i, tomando-se como base o eixo do conduto em relação ao PHR; Vi - velocidade média do escoamento na seção i; pi - pressão estática na seção i.

Equação de Bernoulli Pela condição do escoamento em regime permamente, pode-se afirmar que entre as seções (1) e (2) não ocorre, nem acúmulo, nem falta de massa, ou seja: A mesma massa m que atravessa a seção (1), atravessa a seção (2).

Equação de Bernoulli Relembrando os conceitos de energia: Energia Cinética: Energia Potencial de posição: Energia Potencial de Pressão:

Equação de Bernoulli Energia Mecânica Total em uma Seção do Escoamento Unidirecional, Incompressível em Regime Permanente: A energia total representa a somatória da energia cinética , energia potencial de posição e energia potencial de pressão:

Equação de Bernoulli Carga Mecânica Total em uma Seção do Escoamento Unidirecional, Incompressível em Regime Permanente (Hi): Pela condição do escoamento se dar em regime permanente podemos afirmar que tanto a massa (m), como o peso (G) do fluido, que atravessa uma dada seção do escoamento, é constante ao longo do mesmo; Por este motivo, é comum considerar a energia, ou por unidade de massa, ou por unidade de peso do fluido, além disto, esta consideração origina uma unidade facilmente visualizada: a carga.

Equação de Bernoulli Carga Mecânica Total em uma Seção do Escoamento Unidirecional, Incompressível em Regime Permanente (Hi): Define-se carga como sendo a relação da energia pelo peso do fluido, portanto a carga total em uma seção i (Hi), pode ser definida como mostramos a seguir:

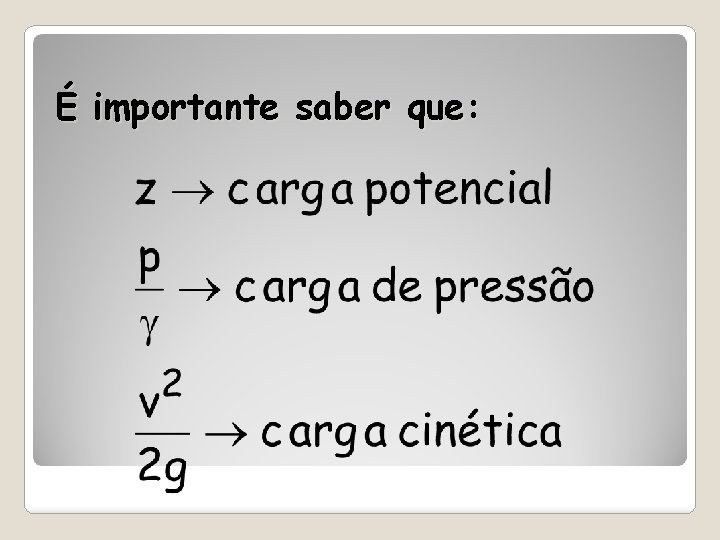
É importante saber que:

Conservação da Energia Partindo do Teorema do Transporte de Reynolds: Para deduzir a formulação para o volume de controle da conservação da quantidade de movimento, fazemos:

Conservação da Energia Variação da Energia no Sistema Variação da Energia com o tempo no V. C. Fluxos de entrada e saída de Energia através da S. C. Conservação da Energia em um volume de controle

Conservação da Energia Os estados inicial e final de energia de um sistema dependem do calor adicionado ou retirado e do trabalho realizado sobre ou pelo o sistema: d. Q = Calor agregado ou retirado ao sistema d. W = Trabalho realizado d. E = Variação da Energia

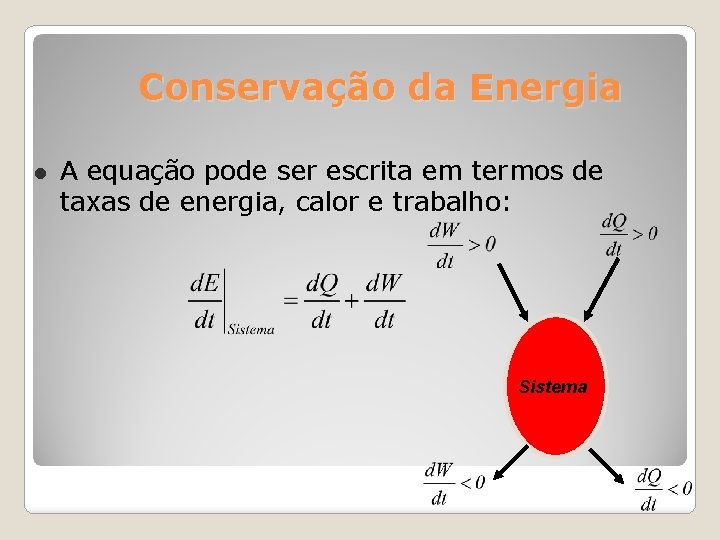
Conservação da Energia A equação pode ser escrita em termos de taxas de energia, calor e trabalho: Sistema

Conservação da Energia Examinando cada termo: Condução, convecção e radiação (considerado como um termo único) Realizado por um eixo, pressão e tensões Viscosas (o trabalho das forças gravitacionais é incluido na energia potencial)

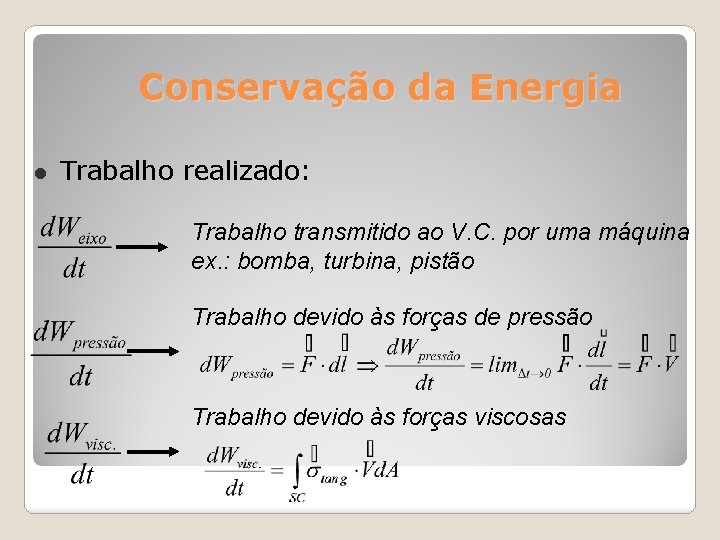
Conservação da Energia Trabalho realizado: Trabalho transmitido ao V. C. por uma máquina ex. : bomba, turbina, pistão Trabalho devido às forças de pressão Trabalho devido às forças viscosas

Conservação da Energia Variação da Energia no Sistema Variação da Energia com o tempo no V. C. Fluxos de entrada e saída de Energia através da S. C. Conservação da Energia em um volume de controle

Casos Especiais Escoamento permanente: 0

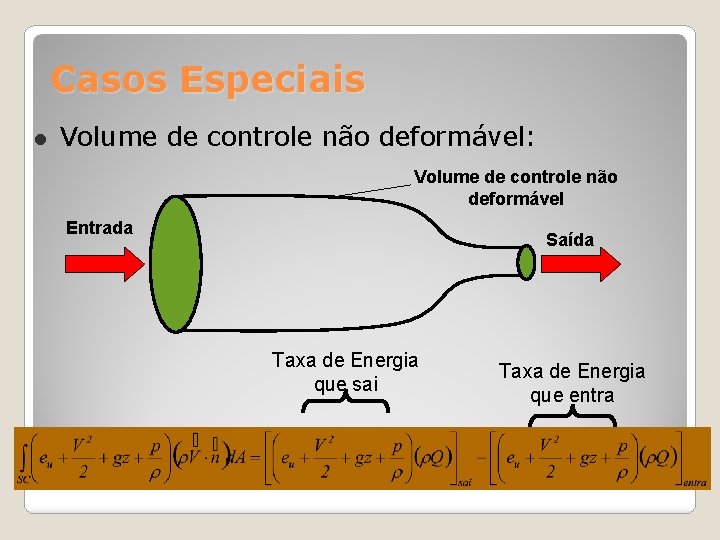
Casos Especiais Volume de controle não deformável: Volume de controle não deformável Entrada Saída Taxa de Energia que sai Taxa de Energia que entra

Equação de Bernoulli Caso particular da Equação da Conservação de Energia; Aplicada à um tubo de corrente.

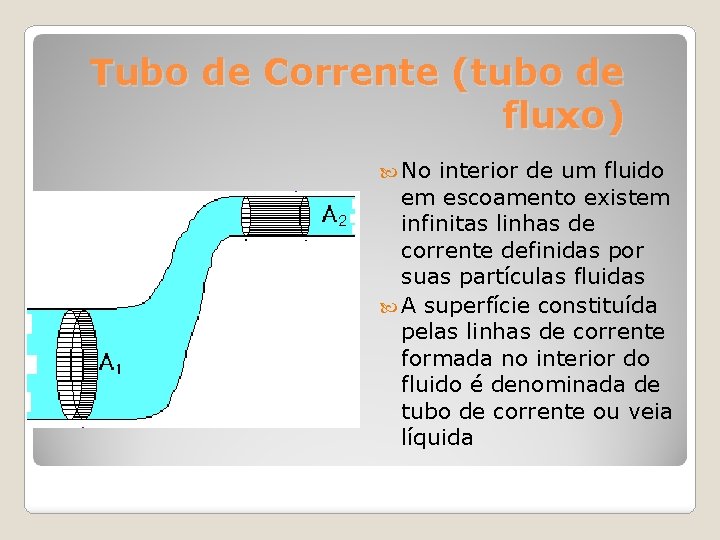
Tubo de Corrente (tubo de fluxo) No interior de um fluido em escoamento existem infinitas linhas de corrente definidas por suas partículas fluidas A superfície constituída pelas linhas de corrente formada no interior do fluido é denominada de tubo de corrente ou veia líquida

Equação de Bernoulli Partindo da Equação da Conservação de Energia, considerando escoamento permanente:

Equação de Bernoulli Em um tubo de corrente não deformável (escoamento laminar):

Equação de Bernoulli Dividindo todos os termos por: e considerando ρ constante:

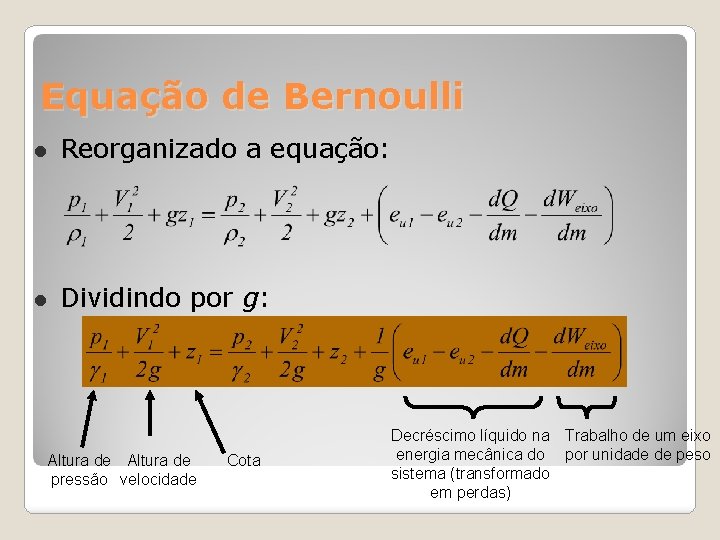
Equação de Bernoulli Reorganizado a equação: Dividindo por g: Altura de pressão velocidade Cota Decréscimo líquido na Trabalho de um eixo energia mecânica do por unidade de peso sistema (transformado em perdas)

Equação de Bernoulli A equação pode ser escrita em termos de cotas: Energia em 1 Energia em 2 Energia Perdida por fornecida (+) ou atrito e calor retirada (-) por um eixo Equação de Bernoulli modificada

Equação de Bernoulli Considerando as seguintes suposições: Escoamento permanente e laminar; Não há perdas por atrito; Não há eixo realizando ou fornecendo trabalho; Não há transformação de calor; A energia interna é constante em dois pontos. Equação de Bernoulli “A energia ao longo de um tubo de corrente é constante”

É importante saber que:

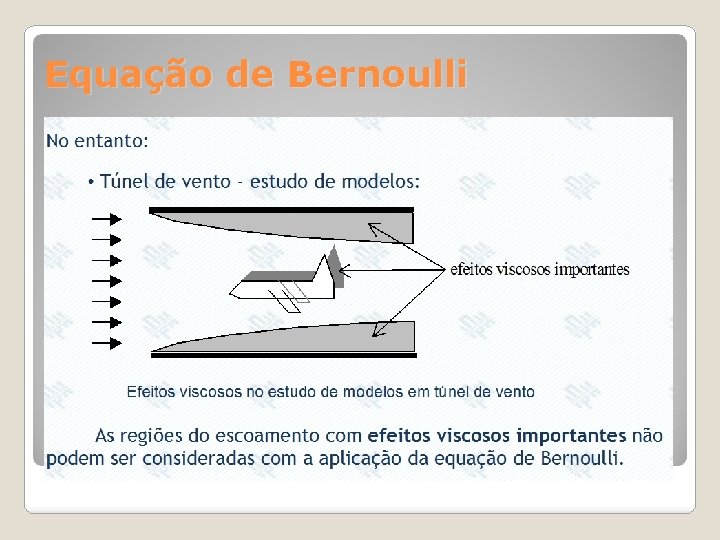
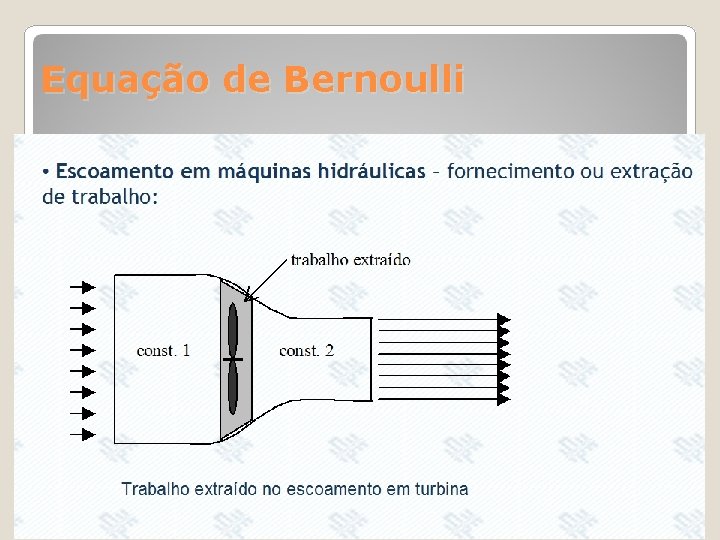
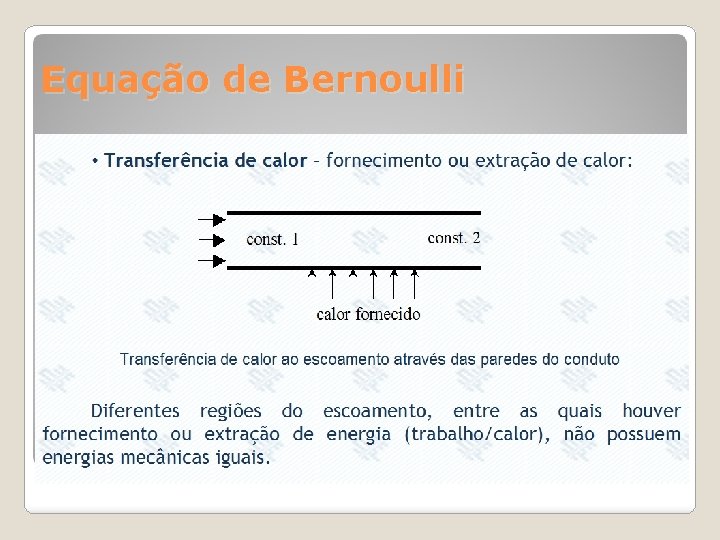
Equação de Bernoulli

Equação de Bernoulli

Equação de Bernoulli

Equação de Bernoulli

Equação de Bernoulli Linha de energia

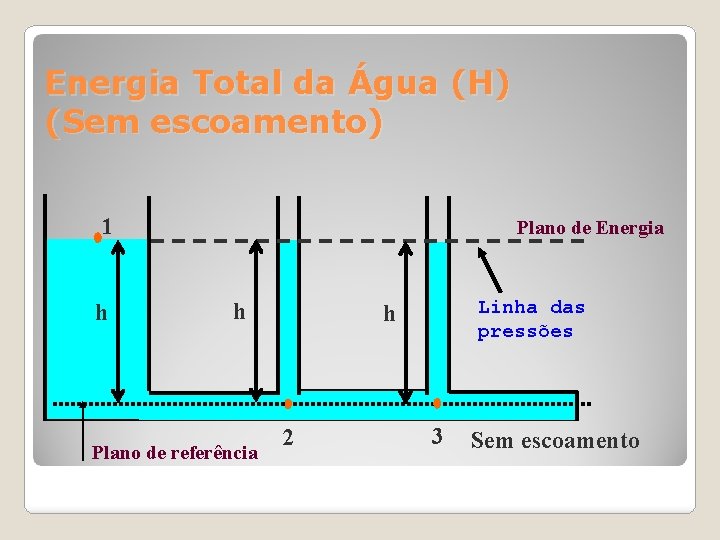
Energia Total da Água (H) (Sem escoamento) 1 h Plano de Energia h Plano de referência Linha das pressões h 2 3 Sem escoamento

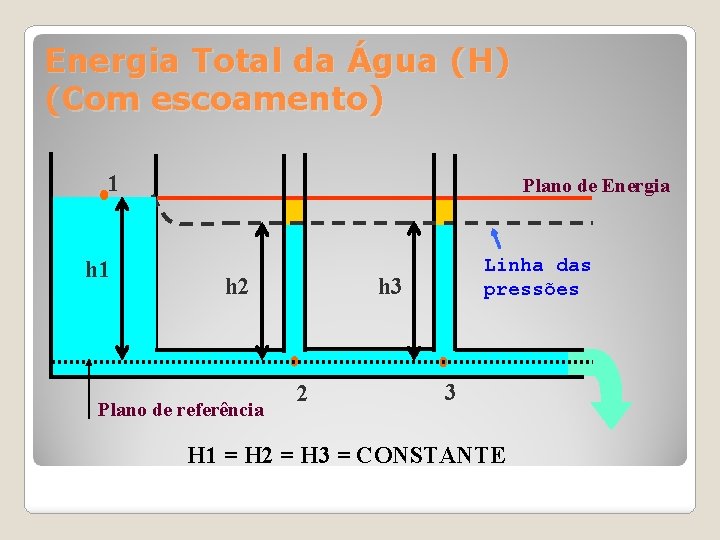
Energia Total da Água (H) (Com escoamento) 1 h 1 Plano de Energia h 2 Plano de referência Linha das pressões h 3 2 3 H 1 = H 2 = H 3 = CONSTANTE

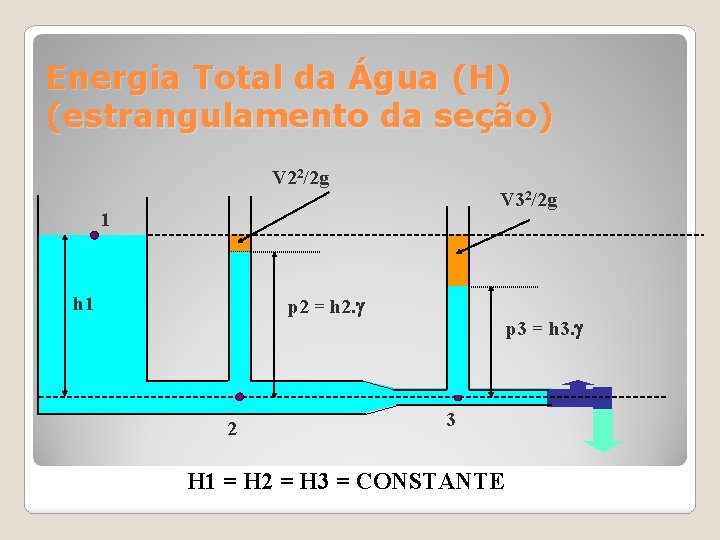
Energia Total da Água (H) (estrangulamento da seção) V 22/2 g V 32/2 g 1 h 1 p 2 = h 2. p 3 = h 3. 2 3 H 1 = H 2 = H 3 = CONSTANTE

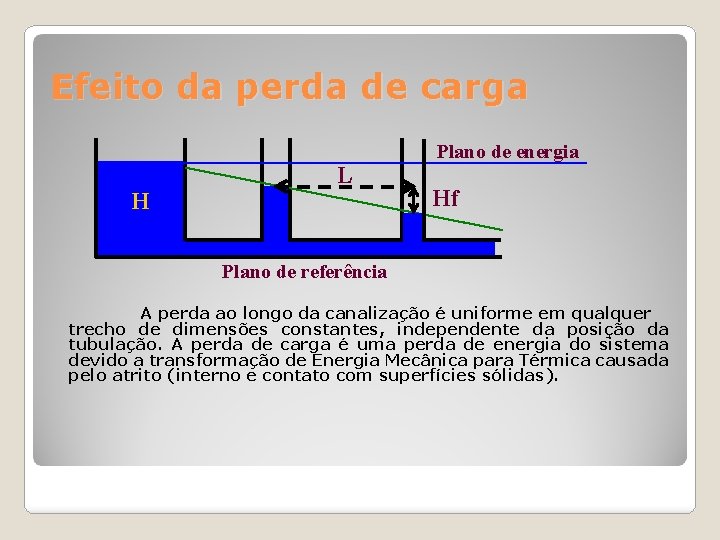
Efeito da perda de carga L H Plano de energia Hf Plano de referência A perda ao longo da canalização é uniforme em qualquer trecho de dimensões constantes, independente da posição da tubulação. A perda de carga é uma perda de energia do sistema devido a transformação de Energia Mecânica para Térmica causada pelo atrito (interno e contato com superfícies sólidas).

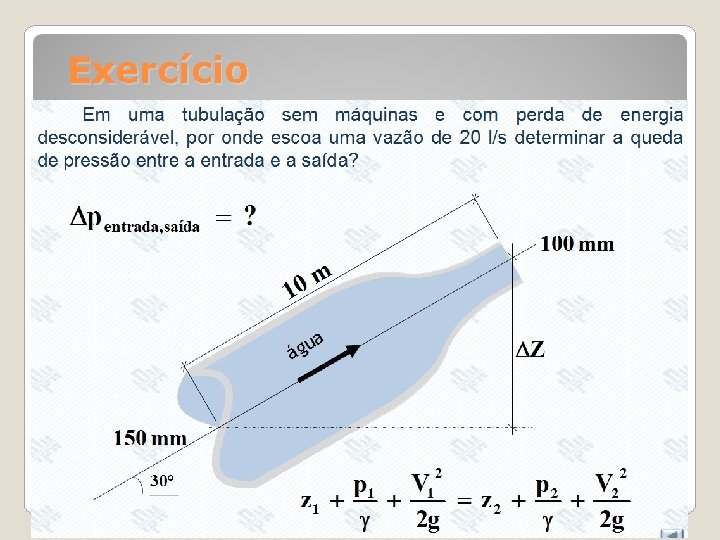
Exercício

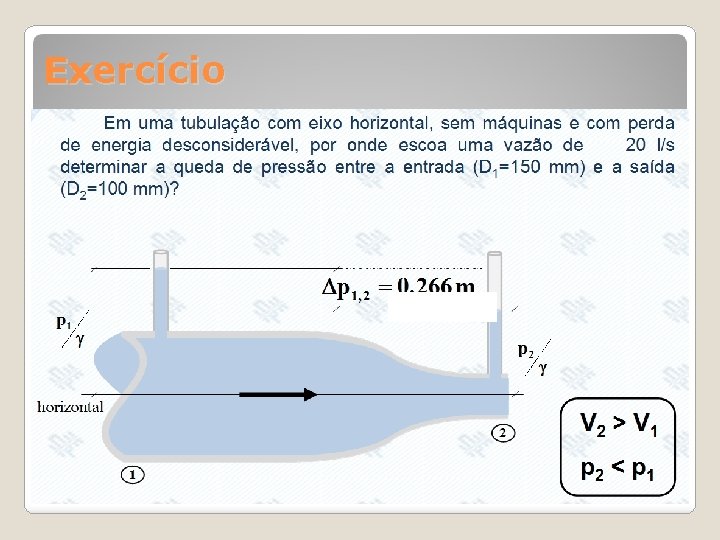
Exercício

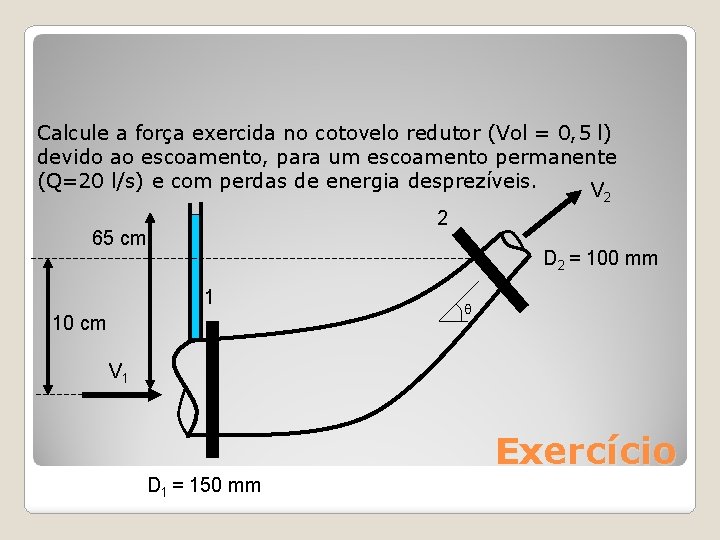
Calcule a força exercida no cotovelo redutor (Vol = 0, 5 l) devido ao escoamento, para um escoamento permanente (Q=20 l/s) e com perdas de energia desprezíveis. V 2 2 65 cm D 2 = 100 mm 1 10 cm θ V 1 Exercício D 1 = 150 mm