MechatronicsGreen Energy Lab Lecture 1 ECE 842 Online

Load Flow Equations • Given: Schedule of generations, loads and the system model The power balance equation for a power system network can be written as S=P+j. Q (1) = T. * = T. ( Y )* Where S is the complex power injection vector P is real power injection vector Q is reactive power injection vector is the current injection vector is the bus voltage vector Y = G + j B is the system admittance matrix

• In polar coordinate system, the complex voltage and the calculated real and reactive powers can be written as (2) i = Vi (cos i + j sin i) (3) (4) Where, ij i - j In Cartesian coordinate system, Eq. (2), Eq. (3) and Eq. (4) can be rewritten as i = ei + j f i (5) (6) (7) Where, n: is the number of buses in the system.

Solution Methods Newton-Raphson (NR) Method • The load flow equations given by equations (3) and (4) can be expanded into Taylor series and the following first order approximation can be obtained: (8) (9)

• Where, J is the Jacobian matrix whose elements are listed in [9]. The Jacobian matrix is evaluated at V = Vk and = k. Vk = Vk+1 - Vk. k = k+1 - k. Pk = PSp – PCal, k. Qk = QSp – QCal, k. PSp , QSp are the specified net active and reactive power injection vectors. PCal, k , QCal, k are the calculated net active and reactive power injection vectors at iteration k, using Vk and k. k: iteration count • For swing bus, Vi and Qi are set equal to zero. For P-V buses, the Vi are set equal to zero. • Notice that for a P-V bus, the reactive power generation has to be calculated and checked for violation of Q-limits. • In case of limit violations, the bus type has to be switched from PV to PQ type on order to maintain the reactive generation within the specified limits. • This procedure is intentionally delayed until after the first little iteration, in order to avoid the unnecessary bus type switching [6].

Fast Decoupled Load Flow (FDLF) Method • • • The fast decoupled load flow algorithm is a modified version of the NR method. The FDLF algorithm takes advantage of the weak coupling between the real and reactive powers and uses two constant matrices to approximate and decouple the Jacobian matrix. The FDLF algorithm can be summarized as: (10) (11) • Where B`` is the imaginary part of the Y matrix and B` is the same as B`` except for the line resistances and shunt elements which are neglected. The order of B` is one less than the system size while the order B`` is determined by the number of PQ buses in the system.

Second Order Load Flow (SOLF) Method • Notice that Eq. (1) is a second order complex equation in and so are Eq. (6) and Eq. (7) in Cartesian coordinate system. If we expand Eq. (6) and Eq. (7), into Taylor series: (12) (13) • In more compact form, we have (14) (15)

• Where elements is the second term vector, and J, is the Jacobian matrix, the of which are listed in [10]. It can be shown that [7] the second order term can be simplified as (16) • • (17) For Eq. (14), an important observation is that no third or higher order terms are present. Thus if we can solve f and e in Eq. (14), we would expect to obtain the exact solution in one iteration. However, the second order terms are functions of e and f and we are confronted with the same problem. If we ignore the second order terms, we will have the NR algorithm in rectangular coordinates. Instead of ignoring the second order terms completely, we estimate them based on the previous iteration e and f increments. Therefore, the [ P Q] is corrected by the second order term as: (18)

• For a P-V bus, the voltage magnitude is fixed, thus the increments of ei and fi must satisfy: • • (19) Therefore the reactive power equation for a P-V bus will be replaced by the above equation. Moreover, the arrangement of Eq. (15) makes the Jacobian matrix nearly diagonally dominant, which improves the condition number for the Jacobian matrix. The Second Order Load Flow (SOLF) algorithm is thus summarized as: • 1. Initialize all the arrays. 2. Set SP and SQ vectors equal to zero. 3. Compute the PCal and QCal vectors. If a PV bus Qg violates the limit, then set Qg at the limit. 4. Compute the power mismatches P, Q. If the maximum P , stop. 5. Calculate J matrix. 6. Calculate e and f using: 7. Update the voltages: 8. 9. , Calculate the second order terms SP and SQ using e and f. Go to step 3.

• Notice that in step (3), the Qg for PV buses is calculated by: • Moreover in computing QCal and PCal, Eq. (6) and Eq. (7) are only used in the first iteration when QCal and PCal need to be computed. After that, the new PCal and QCal are computed recursively using Eq. (14) that is: (20) • Since is calculated in the last iteration by: (21) • Substituting into Eq. (2): (22)

Gauss-Seidel (GS) Method • The Gauss-Seidel method uses the original power balance equations to successively improve the accuracy of the bus voltages starting from an initial guess. Eq. (1) can be rewritten in the following form by rearranging the terms: (23) • The right hand side of the equation is evaluated using the most recent updates of the voltages at the rest of the buses. For P-V type buses, Qk is substituted by its calculated value and the magnitude of the updated voltage is corrected according to the specified bus voltage.

Performance Comparisons Memory Requirements • • Using the sparsity storage scheme for the admittance and the Jacobian matrices, the memory requirements (in Bytes) are listed in table I. The given figures assume that double precision arithmetic is employed all through out the calculations. Although the exact memory requirements depend heavily on the programming techniques, they are not expected to deviate considerably from the estimates given in table I. it can be observed that the memory requirements for the GS, FDLF, NR and SOLF algorithms are increasing in the respective order. Table I indicates that, large electric power systems of over 1000 buses can be readily solved using such personal computers. The PC used in this study has 30 MB hard disk, 1. 2 MB floppy disk and 1 MB of working memory available for processing.

CPU – time Requirements • • • The CPU time requirements of the four algorithms under full load conditions recorded on the PC computer are shown in table II. The X’s appearing in this and some of the following tables indicate that the runs for these cases took significantly longer CPU times than the ones corresponding to the other methods when solving the same test system. Therefore, these runs were terminated and dismissed for practical purposes. Both NR and SOLF methods re-factorize the complete Jacobian at each iteration and thus slow down the computational speed considerably. The input data for the IEEE test systems used in this study are published. Generally speaking, the CPU time also depends on the programming techniques as well as the system under study. Among the systems tested, P-V bus voltages had to be adjusted only for the case of 30 and 118 bus systems. The base case power flows converged without requiring any adjustments in the remaining test cases. For P-V type buses, Qk is substituted by its calculated value and the

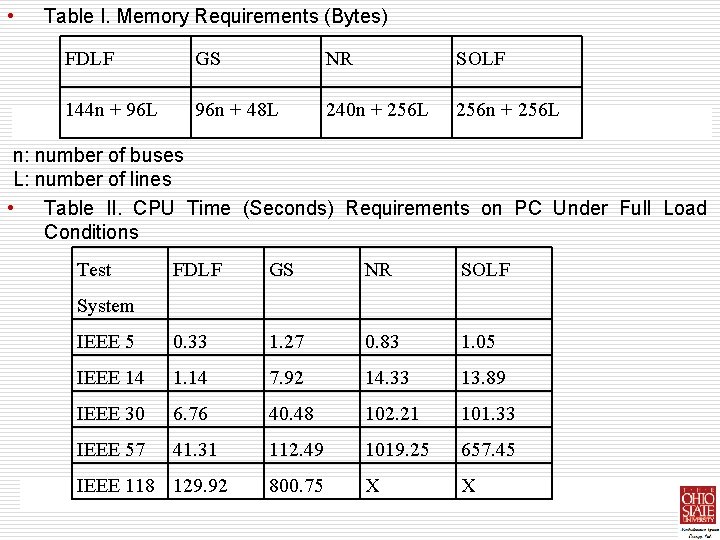
• Table I. Memory Requirements (Bytes) FDLF GS NR SOLF 144 n + 96 L 96 n + 48 L 240 n + 256 L 256 n + 256 L n: number of buses L: number of lines • Table II. CPU Time (Seconds) Requirements on PC Under Full Load Conditions Test FDLF GS NR SOLF IEEE 5 0. 33 1. 27 0. 83 1. 05 IEEE 14 1. 14 7. 92 14. 33 13. 89 IEEE 30 6. 76 40. 48 102. 21 101. 33 IEEE 57 41. 31 112. 49 1019. 25 657. 45 800. 75 X X System IEEE 118 129. 92

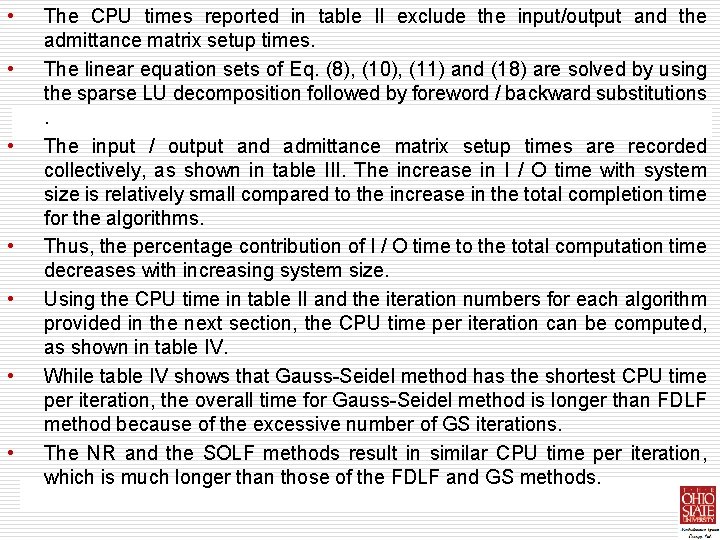
• • The CPU times reported in table II exclude the input/output and the admittance matrix setup times. The linear equation sets of Eq. (8), (10), (11) and (18) are solved by using the sparse LU decomposition followed by foreword / backward substitutions. The input / output and admittance matrix setup times are recorded collectively, as shown in table III. The increase in I / O time with system size is relatively small compared to the increase in the total completion time for the algorithms. Thus, the percentage contribution of I / O time to the total computation time decreases with increasing system size. Using the CPU time in table II and the iteration numbers for each algorithm provided in the next section, the CPU time per iteration can be computed, as shown in table IV. While table IV shows that Gauss-Seidel method has the shortest CPU time per iteration, the overall time for Gauss-Seidel method is longer than FDLF method because of the excessive number of GS iterations. The NR and the SOLF methods result in similar CPU time per iteration, which is much longer than those of the FDLF and GS methods.

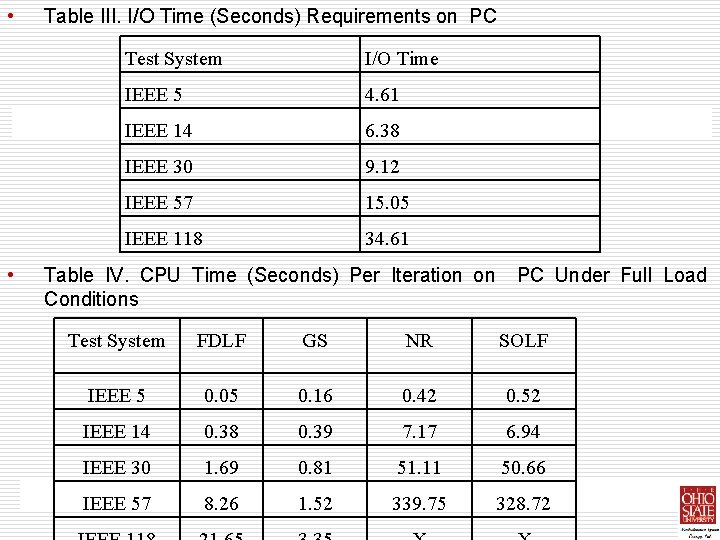
• • Table III. I/O Time (Seconds) Requirements on PC Test System I/O Time IEEE 5 4. 61 IEEE 14 6. 38 IEEE 30 9. 12 IEEE 57 15. 05 IEEE 118 34. 61 Table IV. CPU Time (Seconds) Per Iteration on Conditions PC Under Full Load Test System FDLF GS NR SOLF IEEE 5 0. 05 0. 16 0. 42 0. 52 IEEE 14 0. 38 0. 39 7. 17 6. 94 IEEE 30 1. 69 0. 81 51. 11 50. 66 IEEE 57 8. 26 1. 52 339. 75 328. 72

• Table V. Iteration Numbers Under Full Load Conditions For PC Test FDLF GS NR SOLF IEEE 5 7 8 2 2 IEEE 14 3 20 2 2 IEEE 30 4 50 2 2 IEEE 57 5 74 3 2 239 X X System IEEE 118 6

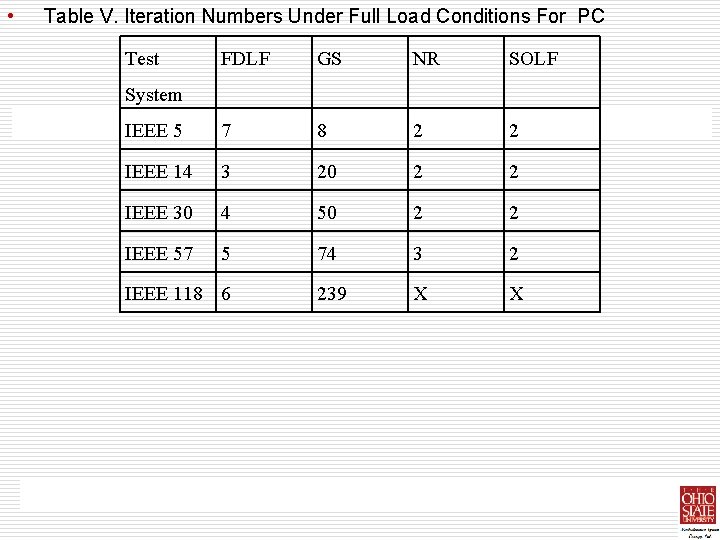
Iteration Requirements • • • Table V shows the total number of iterations needed for the four algorithms to converge, under full load conditions. The mismatch tolerances for the active and reactive power are assumed 0. 01 p. u. As seen from table V, the GS method needs a large number of iterations to converge to a given power mismatch tolerance, compared to the other methods. The FDLF method needs more iteration to converge than the NR and SOLF methods. But as indicated in the last section, the CPU time requirement for FDLF method per iteration is much less than the NR and SOLF methods.

Convergence Characteristics • • • The convergence characteristics of an algorithm is best described by plotting the maximum mismatch at each iteration versus the number of iterations. The mismatch plots give more insights allowing the user to improve the algorithm. Figure 1 through figure 7 show the maximum real (the solid lines) and reactive (the dotted lines) power mismatches of the IEEE 14 bus system as functions of the number of iterations for the FDLF, GS, NR, and SOLF algorithms. For the other test systems the convergence characteristics are very similar and are not shown. The curves are obtained for the full load case. As seen in figures 1 -4 that the mismatches monotonously decrease for all cases under the full load conditions, and the NR method and SOLF method exhibit fastest convergence rate. For FDLF and GS algorithms, the reactive power mismatch decrease faster than the active power mismatch, therefore the convergence rate depends on the real power mismatches. This fact also indicates that the Q-limit adjustments for the PV buses are very effective with these two algorithms. On the other hand, the convergence rates of the real and reactive problems are about the same for the NR and SOLF methods.

Ill-Conditioned Systems with Large R/X Ratios • • • The FDLF algorithm requires one to three extra iterations to converge when the line R/X ratios are increased. The effect of large R/X ratios on the convergence of the GS algorithm varies, depending on the type of system under study. The convergence characteristics The reliability of the four algorithms are studied by increasing the line resistances of the best systems up to 150% of their base values. Depending on the number of lines having large R/X ratios, the convergence pattern changes. Tables VI, VII and VIII show the required number of iterations for convergence of the four algorithms when two, four and all the system lines R/X ratios are increased respectively. The convergence characteristics of all four algorithms for the 14 bus system with all the lines having increased R/X ratios are given in figures 5 -8 of the NR and SOLF algorithms are not affected much with the increased line R/X ratios. In addition to these tests, a 13 bus test system is also used to test the convergence characteristics of the four algorithms under sever ill-conditioning. The system contains long transmission lines as well as lines with R/X ratios chose to unity, causing the system equations to be ill-conditioned. All algorithms expect for the GS, converged as given in Table IX. The convergence characteristics are also shown in

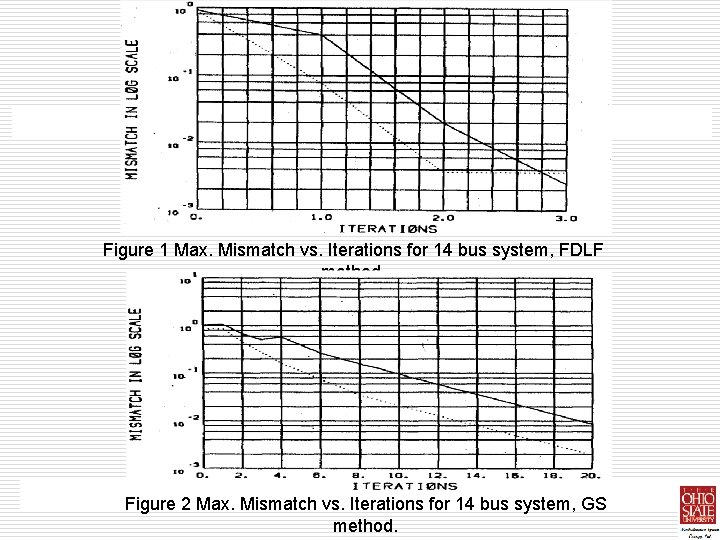
Figure 1 Max. Mismatch vs. Iterations for 14 bus system, FDLF method. Figure 2 Max. Mismatch vs. Iterations for 14 bus system, GS method.

Initial Voltage profiles • • From the convergence characteristics of the GS algorithm, it is observed that at the early stages of iterations, the maximum mismatches decrease monotonously but later on, this rate of decrease slows down. However, as discussed in former section, each GS iteration takes extremely short CPU time per iteration and needs very small amount of memory. Thus the idea of using GS method to set up the favorable initial starting conditions for the FDLF, NR and SOLF algorithms is very attractive. After some experiments, it is found that n iterations by the GS algorithm (n is the system size) will generally give a good starting voltage profiles for the FDLF, NR and SOLF algorithms.

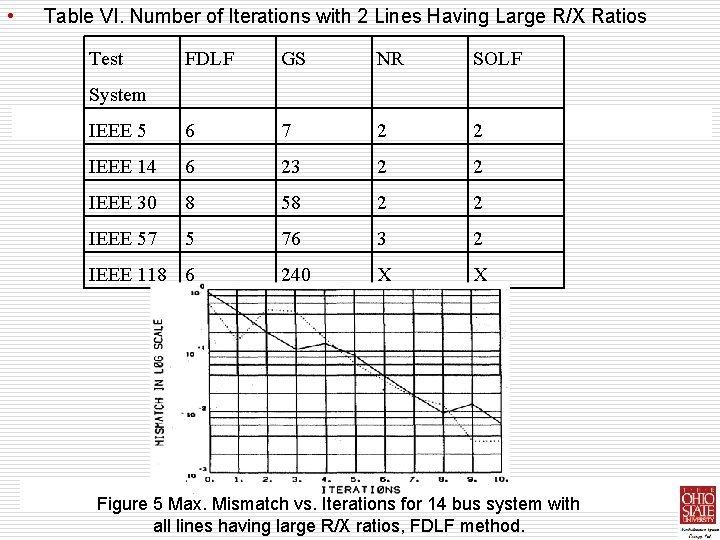
• Table VI. Number of Iterations with 2 Lines Having Large R/X Ratios Test FDLF GS NR SOLF IEEE 5 6 7 2 2 IEEE 14 6 23 2 2 IEEE 30 8 58 2 2 IEEE 57 5 76 3 2 240 X X System IEEE 118 6 Figure 5 Max. Mismatch vs. Iterations for 14 bus system with all lines having large R/X ratios, FDLF method.

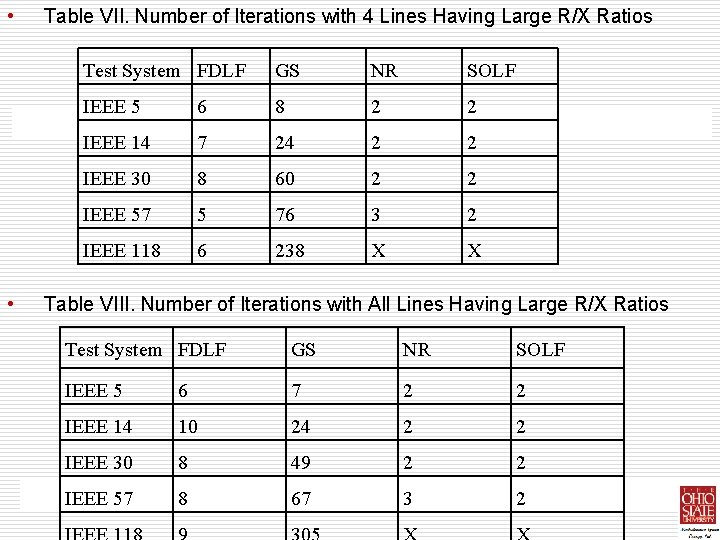
• • Table VII. Number of Iterations with 4 Lines Having Large R/X Ratios Test System FDLF GS NR SOLF IEEE 5 6 8 2 2 IEEE 14 7 24 2 2 IEEE 30 8 60 2 2 IEEE 57 5 76 3 2 IEEE 118 6 238 X X Table VIII. Number of Iterations with All Lines Having Large R/X Ratios Test System FDLF GS NR SOLF IEEE 5 6 7 2 2 IEEE 14 10 24 2 2 IEEE 30 8 49 2 2 IEEE 57 8 67 3 2

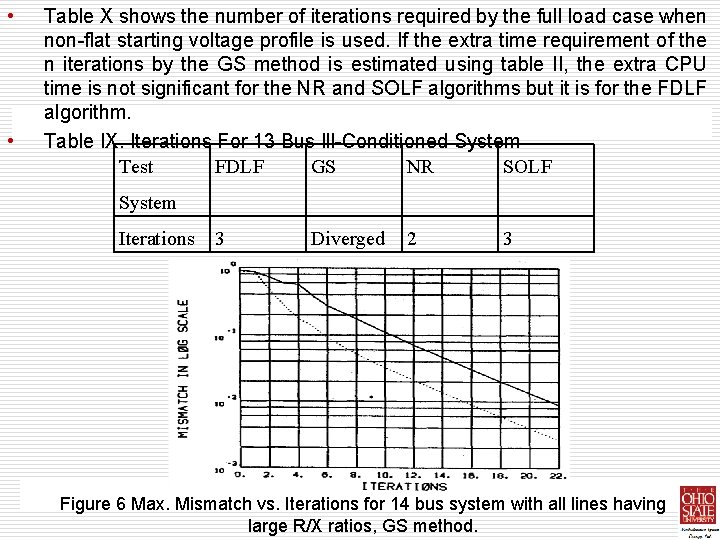
• • Table X shows the number of iterations required by the full load case when non-flat starting voltage profile is used. If the extra time requirement of the n iterations by the GS method is estimated using table II, the extra CPU time is not significant for the NR and SOLF algorithms but it is for the FDLF algorithm. Table IX. Iterations For 13 Bus Ill-Conditioned System Test FDLF GS NR SOLF System Iterations 3 Diverged 2 3 Figure 6 Max. Mismatch vs. Iterations for 14 bus system with all lines having large R/X ratios, GS method.

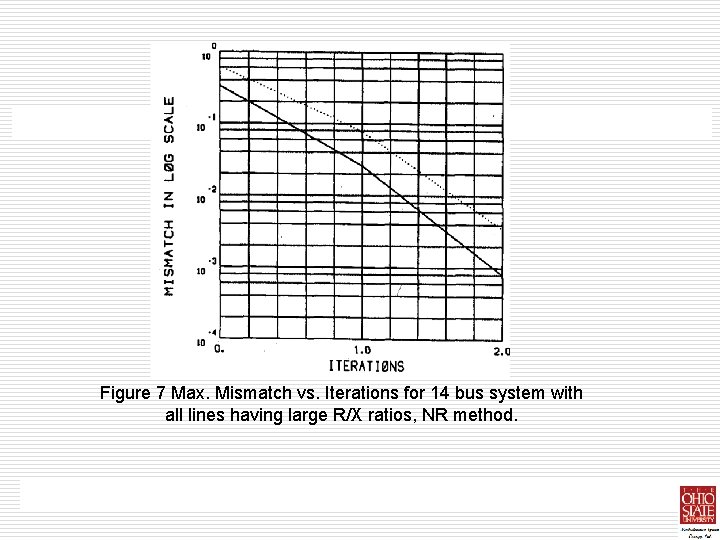
Figure 7 Max. Mismatch vs. Iterations for 14 bus system with all lines having large R/X ratios, NR method.

• • • Figure 12 -14 show the convergence characteristic of the FDLF, NR, and SOLF algorithms using non-flat starting voltages for full load case of the IEEE 14 bus system. These simulations imply that the favorable initial starting voltages reduce the iteration requirements as well as the total solution times for the NR and SOLF algorithms. For instance, the solution time for the 57 bus system can be reduced from over 1000 seconds to about 400 seconds when non-flat starting voltages are used. However, this approach is not suitable for the FDLF algorithm since the extra CPU time needed is much longer than a single iteration of a FDLF algorithm. Figure 8 Max. Mismatch vs. Iterations for 14 bus system with all lines having large R/X ratios, SOLF method.

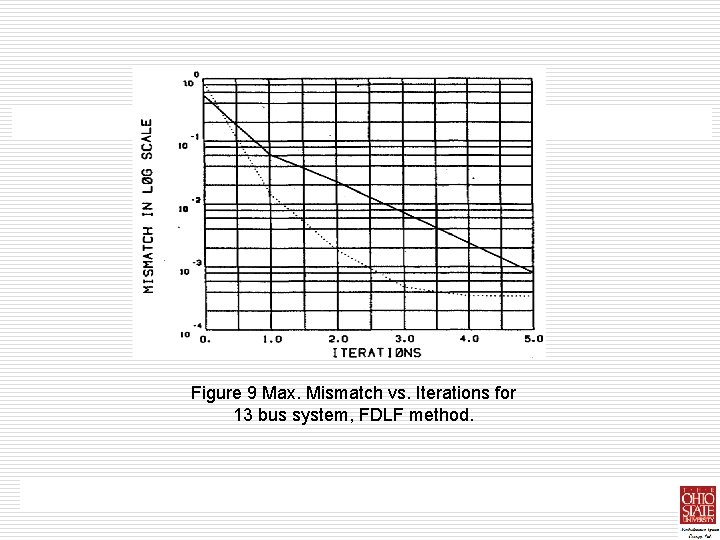
Figure 9 Max. Mismatch vs. Iterations for 13 bus system, FDLF method.

The Precision Effect on The Number of Iterations • • When solving large systems on a PC which has a limited memory, the use of single precision arithmetic may be necessary. In order to assess the effects of such a constraint on the performance of one of the studied algorithms, namely FDLF, the same program was run using both double and single precision for the 5, 14, 30, 57 and 118 bus test systems. The results indicate that the precision does not affect the convergence patterns significantly. Table XI and XII show the maximum mismatch vs. iterations for the 14 bus test system usingle and double precision. The mismatches calculated for the two cases do not differ more than 10 -6 p. u. which is negligible for most power system applications.

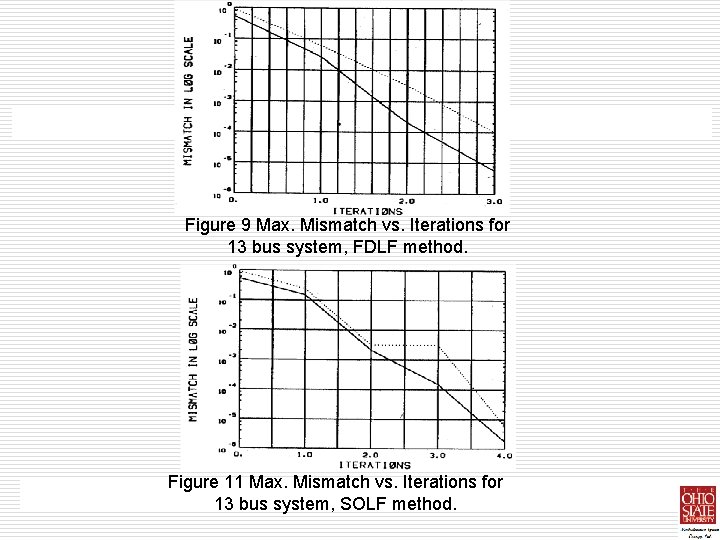
Figure 9 Max. Mismatch vs. Iterations for 13 bus system, FDLF method. Figure 11 Max. Mismatch vs. Iterations for 13 bus system, SOLF method.

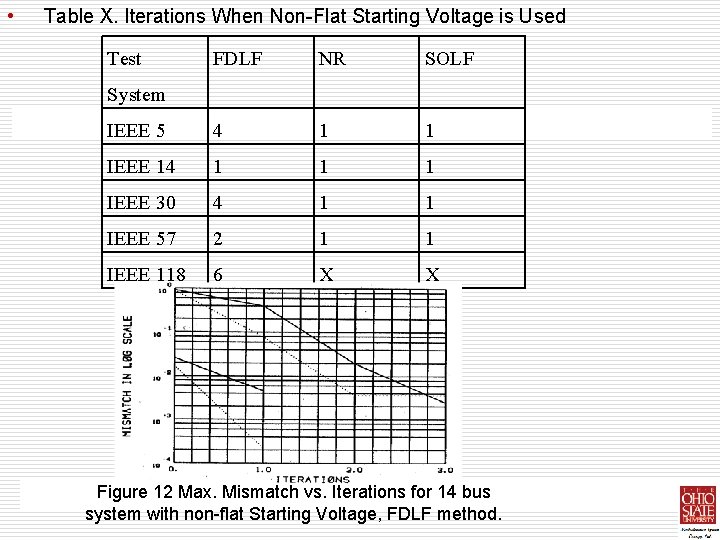
• Table X. Iterations When Non-Flat Starting Voltage is Used Test FDLF NR SOLF IEEE 5 4 1 1 IEEE 14 1 1 1 IEEE 30 4 1 1 IEEE 57 2 1 1 IEEE 118 6 X X System Figure 12 Max. Mismatch vs. Iterations for 14 bus system with non-flat Starting Voltage, FDLF method.

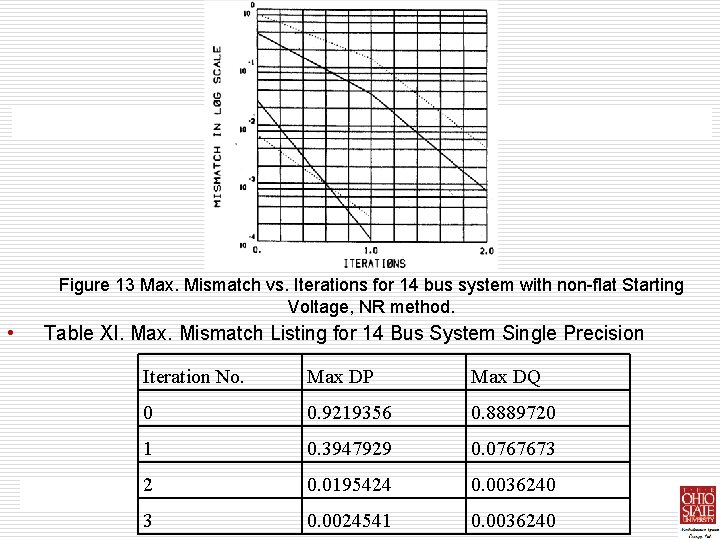
Figure 13 Max. Mismatch vs. Iterations for 14 bus system with non-flat Starting Voltage, NR method. • Table XI. Max. Mismatch Listing for 14 Bus System Single Precision Iteration No. Max DP Max DQ 0 0. 9219356 0. 8889720 1 0. 3947929 0. 0767673 2 0. 0195424 0. 0036240 3 0. 0024541 0. 0036240

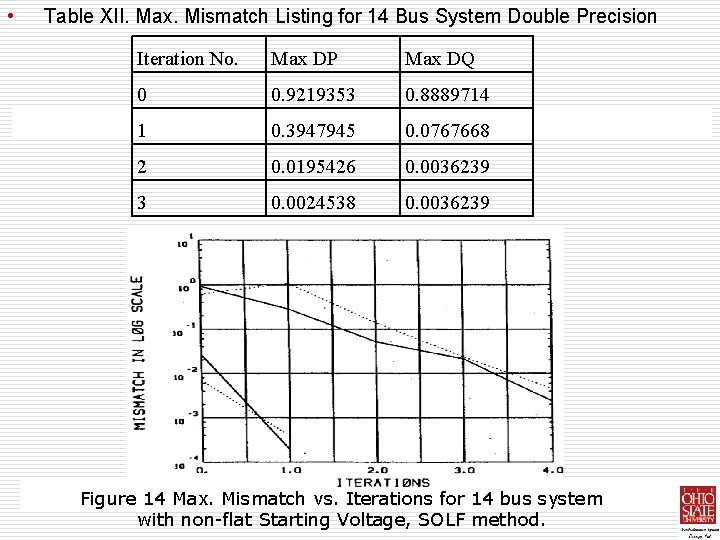
• Table XII. Max. Mismatch Listing for 14 Bus System Double Precision Iteration No. Max DP Max DQ 0 0. 9219353 0. 8889714 1 0. 3947945 0. 0767668 2 0. 0195426 0. 0036239 3 0. 0024538 0. 0036239 Figure 14 Max. Mismatch vs. Iterations for 14 bus system with non-flat Starting Voltage, SOLF method.

Conclusions • • • A performance evaluation of the PC for running power flow programs is presented. Four different algorithm namely FDLF, GS, NR and SOLF are implemented and case studies are carried out for 5, 14, 30, 57 and 118 bus test power systems. The data gathered via simulations are analyzed with regard to the run times, convergence patterns, initial conditions, employed arithmetic precision and illconditioning of the system equations. The well known properties of these algorithms are confirmed by the case study results. The NR method is reliable and rapid in convergence, whereas the GS is slower and may even fail to converge under severe ill-conditioning. Experimenting with the algorithms indicated that favorable starting values for other algorithms could be obtained by initially running n GS iterations, where n is the system size. This resulted in convergence speed-ups for the NR and SOLF algorithms. In general the SOLF algorithm seemed to take the least number of iterations to converge due to the corrections accounting for the second order terms at each iteration. Also, the overall computation load for Pcal, Qcal calculations is reduced via the recursive formulations employed as described in the chapter.