MECHANIKA KERESZTMETSZETI JELLEMZK SZCHENYI EGYETEM Szerkezetptsi Tanszk MECHANIKA

MECHANIKA KERESZTMETSZETI JELLEMZŐK SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék MECHANIKA I. Keresztmetszeti jellemzők

A KERESZTMETSZETI JELLEMZŐK A rúdszerkezetek méretezése során nem elegendő ismerni a keresztmetszet egészére ható erőket (igénybevételeket), hanem az anyagi kapcsolatot pontonként helyettesítő fajlagos belső erőket (feszültségeket) kell összehasonlítani az alkalmazott anyag ellenállásával, terhelhetőségével, szilárdságával. Ehhez a keresztmetszeti síkidom jellemző mennyiségeire (is) szükség van. A következőkben a legfontosabb keresztmetszeti jellemzők definícióit, tulajdonságait és előállításuk algoritmusait tárgyaljuk. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék MECHANIKA I. Keresztmetszeti jellemzők 2

A TÁRGYALT KERESZTMETSZETI JELLEMZŐK • NULLADRENDŰ NYOMATÉK – TERÜLET • ELSŐRENDŰ NYOMATÉK – STATIKAI NYOMATÉK • MÁSODRENDŰ NYOMATÉK – TEHETETLENSÉGI/INERCIA NYOMATÉK – CENTRIFUGÁLIS/DEVIÁCIÓS NYOMATÉK SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék MECHANIKA I. Keresztmetszeti jellemzők 3

A KERESZTMETSZETI JELLEMZŐK ELŐÁLLÍTÁSI MÓDSZERE Dy Dx SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék A gondolatmenetet a terület meghatározása kapcsán mutatjuk be, de a többi jellemző előállítása során is alkalmazzuk. Készítsünk egyenletes osztású négyzet (téglalap) hálózatot, és jelöljük meg azokat az elemeket, amelyek teljes egészükben a vizsgálandó síkidom kontúrvonalán belül vannak. Ezeket összegezve a síkidom területének alsó korlátját kapjuk meg. MECHANIKA I. Keresztmetszeti jellemzők 4

A KERESZTMETSZETI JELLEMZŐK ELŐÁLLÍTÁSI MÓDSZERE Dy Dx A gondolatmenetet a terület meghatározása kapcsán mutatjuk be, de a többi jellemző előállítása során is alkalmazzuk. Készítsünk egyenletes osztású négyzet (téglalap) hálózatot, és jelöljük meg azokat az eleme-ket, amelyekkel a teljes vizsgálandó síkidom lefedhető, úgy hogy annak kontúrvonala mindenütt a lépcsősábrán belül marad. Ezeket összegezve a síkidom területének felső korlátját kapjuk meg. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék MECHANIKA I. Keresztmetszeti jellemzők 5

A KERESZTMETSZETI JELLEMZŐK ELŐÁLLÍTÁSI MÓDSZERE Dy Dx A gondolatmenetet a terület meghatározása kapcsán mutatjuk be, de a többi jellemző előállítása során is alkalmazzuk. A belülről közelítő és a kívülről közelítő lefedettséget egy ábrába rajzolva láthatjuk, ez az eljárás meglehetősen pontatlan, az alsó és a felső korlát között nagy a távolság. Ha a pontosságot e módszer alkalmazása mellett kívánjuk növelni, sűrűbb, finomabb felosztásra lesz szükség. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék MECHANIKA I. Keresztmetszeti jellemzők 6

A KERESZTMETSZETI JELLEMZŐK ELŐÁLLÍTÁSI MÓDSZERE Dx A háló felosztását finomítva látható, hogy a kék színű, minoráns és a piros színű majoráns terület mennyivel jobban közelíti a valódi terület nagyságát. A felosztás minden határon túli finomításával a minoráns és a majoráns terület határértéke megegyezik, és pontosan adja meg a görbe vonallal határolt terület nagyságát. Dy SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék MECHANIKA I. Keresztmetszeti jellemzők 7

A KM. SÍKIDOM TERÜLETE A terület meghatározása történhet a síkidom. BA ill. a síkidom KÖRÉ rajzolható, ismert területű téglalapok területösszegének meghatározásával. Így a tényleges terület alsó ill. felső korlátja állítható elő. Ha az elemi téglalap területét minden határon túl csökkentjük, határátmenetben a síkidom TÉNYLEGES területét kapjuk meg. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék MECHANIKA I. Keresztmetszeti jellemzők 8

A KM. JELLEMZŐK MATEMATIKAI DEFINÍCIÓI Az általános helyzetű elemi síkidom területösszegének, első- ill. másodrendű nyomatékai összegének szummázása az elemi síkidom oldalainak mindenhatáron túli csökkentésével a keresett mennyiségek matematikai definícióját, az elvi meghatározás integrálkifejezését szolgáltatja. (A tényleges számításban általában nem lesz szükség az integrálásra, csak az integrálás, mint összegzés tulajdonságait használjuk ki. ) SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék MECHANIKA I. Keresztmetszeti jellemzők 9

A POLÁRIS INERCIANYOMATÉK r x y Dx Dy Dx×Dy=DA SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék A tehetetlenségi nyomatékokat mindig egy tengelyre (x, y, x, h, . . . ) számítjuk. A síkból kitekintve értelmezhető a sík normálisára, a z tengelyre vonatkozó tehetetlenségi nyomaték is, amiben a négyzetesen szereplő távolságot a z tengely döféspontjától (a síkbeli koordinátarendszer origójától) mérjük. Az r 2=x 2+y 2, összefüggés alapján pedig általánosan igaz, hogy: MECHANIKA I. Keresztmetszeti jellemzők 10

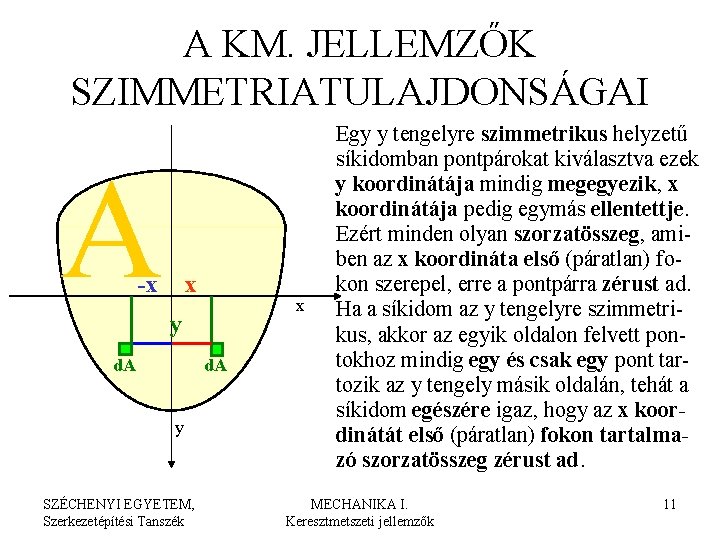
A KM. JELLEMZŐK SZIMMETRIATULAJDONSÁGAI A -x x x y d. A y SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék Egy y tengelyre szimmetrikus helyzetű síkidomban pontpárokat kiválasztva ezek y koordinátája mindig megegyezik, x koordinátája pedig egymás ellentettje. Ezért minden olyan szorzatösszeg, amiben az x koordináta első (páratlan) fokon szerepel, erre a pontpárra zérust ad. Ha a síkidom az y tengelyre szimmetrikus, akkor az egyik oldalon felvett pontokhoz mindig egy és csak egy pont tartozik az y tengely másik oldalán, tehát a síkidom egészére igaz, hogy az x koordinátát első (páratlan) fokon tartalmazó szorzatösszeg zérust ad. MECHANIKA I. Keresztmetszeti jellemzők 11

A KM. JELLEMZŐK ELŐJELTULAJDONSÁGAI A síkidom teljes területének (a feladat lényege alapján) pozitívnak kell lennie (részterület lehet negatív, ha a kiegészített területet ezzel kompenzáljuk). A matematikai definíció alapján (és a szimmetria-tulajdonságok körében kifejtett gondolatmenetnek megfelelően) a statikai nyomaték bármilyen előjelű lehet (ha zérus, a tengely súlyponti tengely!), a centrifugális nyomaték bármilyen előjelű lehet (ha zérus, a tengelyek tehetetlenségi főtengelyek!), az inerciák viszont bármely tengelyre (létező síkidomra!) csak pozitív előjelűek lehetnek. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék MECHANIKA I. Keresztmetszeti jellemzők 12

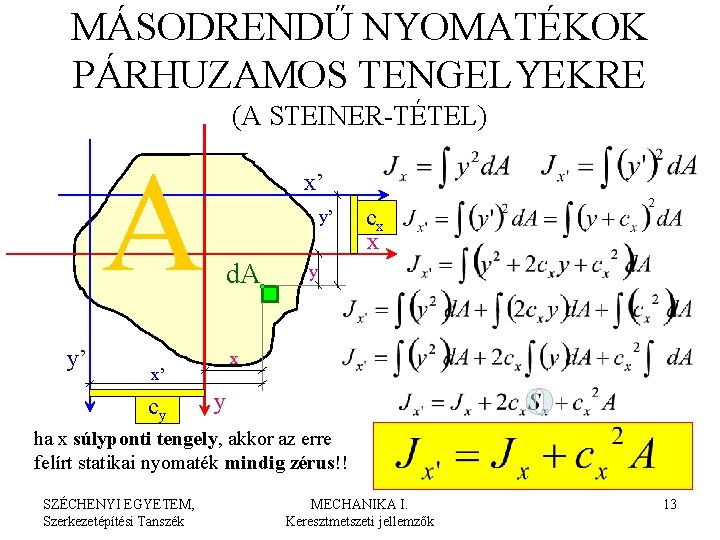
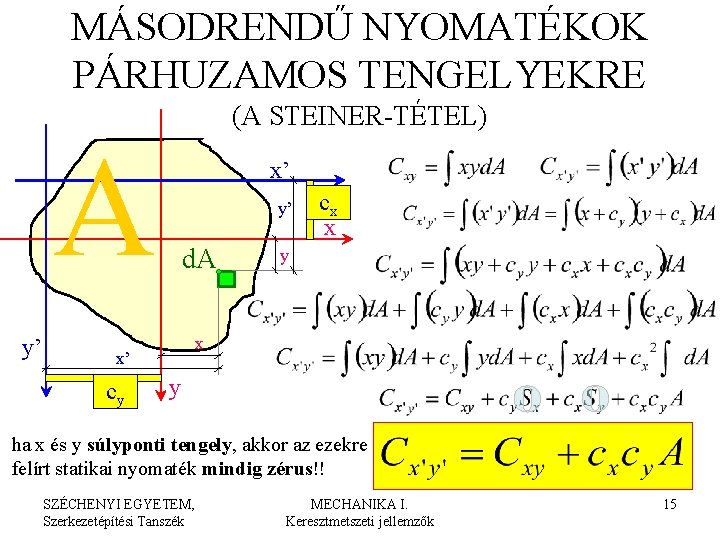
MÁSODRENDŰ NYOMATÉKOK PÁRHUZAMOS TENGELYEKRE (A STEINER-TÉTEL) A y’ x’ y’ d. A y x x’ cy cx x y ha x súlyponti tengely, akkor az erre felírt statikai nyomaték mindig zérus!! SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék MECHANIKA I. Keresztmetszeti jellemzők 13

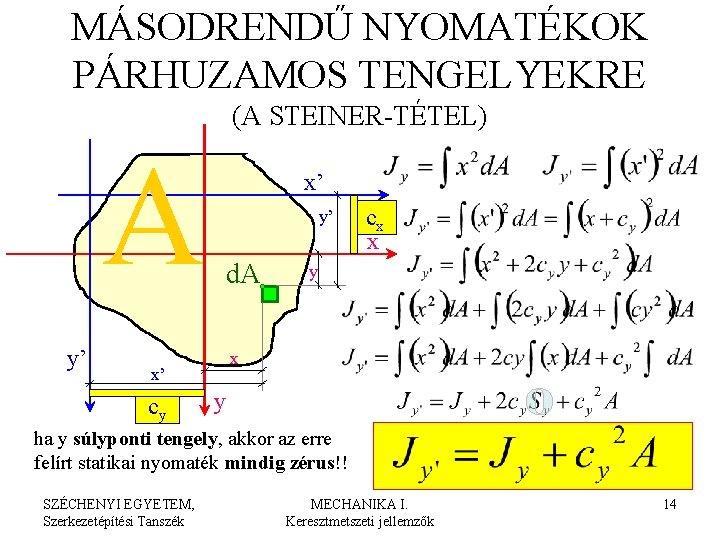
MÁSODRENDŰ NYOMATÉKOK PÁRHUZAMOS TENGELYEKRE (A STEINER-TÉTEL) A y’ x’ y’ d. A y x x’ cy cx x y ha y súlyponti tengely, akkor az erre felírt statikai nyomaték mindig zérus!! SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék MECHANIKA I. Keresztmetszeti jellemzők 14

MÁSODRENDŰ NYOMATÉKOK PÁRHUZAMOS TENGELYEKRE (A STEINER-TÉTEL) A y’ x’ y’ d. A y x x’ cy cx x y ha x és y súlyponti tengely, akkor az ezekre felírt statikai nyomaték mindig zérus!! SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék MECHANIKA I. Keresztmetszeti jellemzők 15

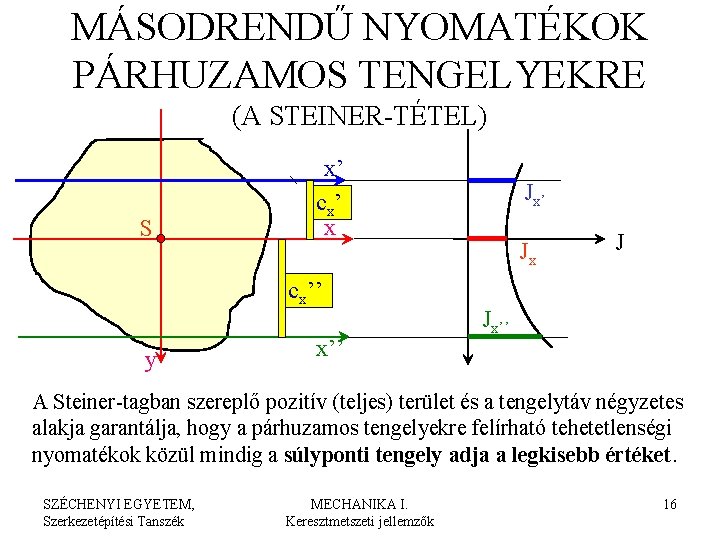
MÁSODRENDŰ NYOMATÉKOK PÁRHUZAMOS TENGELYEKRE (A STEINER-TÉTEL) S x’ c x’ x cx’’ y x’’ Jx J Jx’’ A Steiner-tagban szereplő pozitív (teljes) terület és a tengelytáv négyzetes alakja garantálja, hogy a párhuzamos tengelyekre felírható tehetetlenségi nyomatékok közül mindig a súlyponti tengely adja a legkisebb értéket. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék MECHANIKA I. Keresztmetszeti jellemzők 16

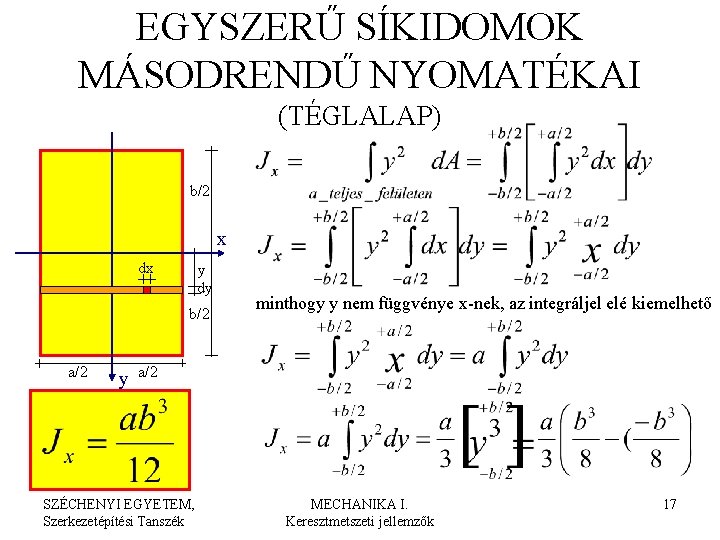
EGYSZERŰ SÍKIDOMOK MÁSODRENDŰ NYOMATÉKAI (TÉGLALAP) b/2 x dx y dy b/2 a/2 y minthogy y nem függvénye x-nek, az integráljel elé kiemelhető a/2 SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék MECHANIKA I. Keresztmetszeti jellemzők 17

EGYSZERŰ SÍKIDOMOK MÁSODRENDŰ NYOMATÉKAI (TÉGLALAP) A téglalap oldalegyenesére a tehetetlenségi nyomaték a STEINER tétel alkalmazásával állítható elő: b/2 x b/2 a/2 y a/2 SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék x’ MECHANIKA I. Keresztmetszeti jellemzők 18

EGYSZERŰ SÍKIDOMOK MÁSODRENDŰ NYOMATÉKAI DERÉKSZÖGŰ HÁROMSZÖG x y d. A=dx×dy x’’ x=a/m×y m y’’ a a derékszögű háromszög tehetetlenségi nyomatéka a csúcson átmenő, és a szemközti befogóval párhuzamos tengelyre: SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék MECHANIKA I. Keresztmetszeti jellemzők 19

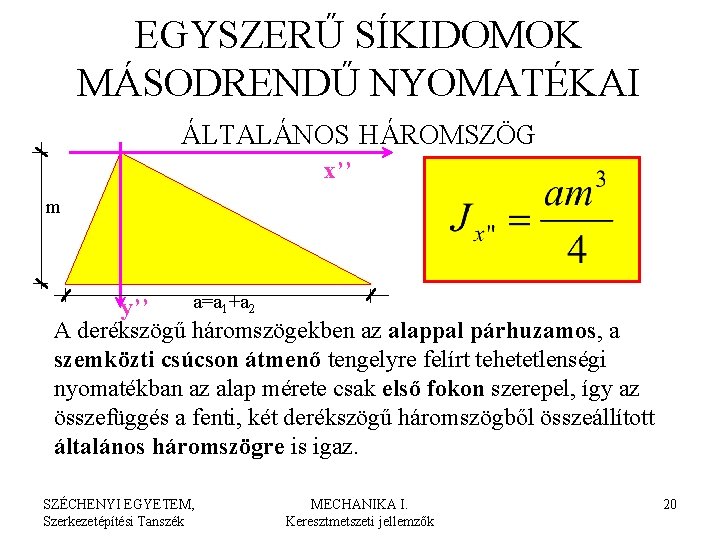
EGYSZERŰ SÍKIDOMOK MÁSODRENDŰ NYOMATÉKAI ÁLTALÁNOS HÁROMSZÖG x’’ m a=a 1+a 2 y’’ A derékszögű háromszögekben az alappal párhuzamos, a szemközti csúcson átmenő tengelyre felírt tehetetlenségi nyomatékban az alap mérete csak első fokon szerepel, így az összefüggés a fenti, két derékszögű háromszögből összeállított általános háromszögre is igaz. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék MECHANIKA I. Keresztmetszeti jellemzők 20

EGYSZERŰ SÍKIDOMOK MÁSODRENDŰ NYOMATÉKAI ÁLTALÁNOS HÁROMSZÖG x’’ m cx’’=2/3 m cx’=1/3 m x x’ a=a 1+a 2 y’’ Az általános háromszög egyik oldalegyenesére ill. a vele párhuzamos súlyponti tengelyre a tehetetlenségi nyomaték a STEINER tétel (értelemszerű) alkalmazásával írható fel. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék MECHANIKA I. Keresztmetszeti jellemzők 21

EGYSZERŰ SÍKIDOMOK MÁSODRENDŰ NYOMATÉKAI ÁLTALÁNOS HÁROMSZÖG x. III y. III x. I y. I x ha az elemi síkidomok szimmetrikusak, akkor x. IV y y. IV A szimmetriatengelyt is tartalmazó tengelykeresztre egy síkidom centrifugális nyomatéka mindig zérus. Az eddigi elemi síkidomok esetében mindig lehetett ilyen tengelykeresztet választani, az általános háromszög esetében azonban nem lehet. Ilyenkor csak az a lehetőség marad, hogy az idomot szimmetrikus (éspedig a globális koordinátarendszer valamelyik tengelyével párhuzamos szimmetriatengelyű) elemekre bontjuk, amelyekre a centrifugális nyomaték zérus, majd minden felbontott elemre meghatározzuk a STEINER tagot, és ezek összege szolgáltatja a teljes síkidom centrifugális nyomatékát a globális tengelykeresztre. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék MECHANIKA I. Keresztmetszeti jellemzők 22

EGYSZERŰ SÍKIDOMOK MÁSODRENDŰ NYOMATÉKAI KÖR r dr d. A=dr×rdfrdf f df A kör esetében célszerűen poláris koordinátarendszert alkalmazva a középpontra vonatkozó poláris inercianyomatékot kaphatjuk meg. A kör szimmetriája alapján azonban ebből adódik, hogy bármely tengelyre a tehetetlenségi nyomaték a poláris tehetetlenségi nyomaték fele lesz. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék MECHANIKA I. Keresztmetszeti jellemzők 23

EGYSZERŰ SÍKIDOMOK MÁSODRENDŰ NYOMATÉKAI FÉLKÖR x x x y x’ x’ y’ y’ y y Jx +Jx =Jx ; Jx’ +Jx’ =Jx ; Jy +Jy =Jy +J =J J A félköry’tehetetlenségi y’ y nyomatéka a szimmetriatengelyére ill. az oldalátmérőre a teljes kör inerciájából egyszerűen származtatható. VIGYÁZAT! A vesszős tengelyek NEM SÚLYPONTI TENGELYEK!!! SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék MECHANIKA I. Keresztmetszeti jellemzők 24

A FÉLKÖR SÚLYPONTJA 2/3 R Rcosf x’ f R y’ df d. A=R×Rdf/2 A súlypont-meghatározást polárkoordinátarendszerben végezhetjük. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék MECHANIKA I. Keresztmetszeti jellemzők 25

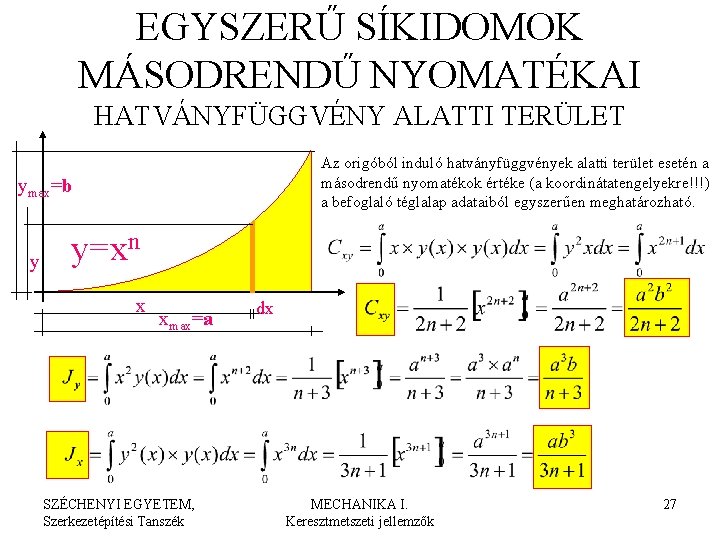
EGYSZERŰ SÍKIDOMOK MÁSODRENDŰ NYOMATÉKAI HATVÁNYFÜGGVÉNY ALATTI TERÜLET ymax=b y y=xn x xmax=a dx Az origóból induló hatványfüggvények alatti terület nagysága és súlypontjának x koordinátája a befoglaló téglalap adataiból egyszerűen meghatározható. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék MECHANIKA I. Keresztmetszeti jellemzők 26

EGYSZERŰ SÍKIDOMOK MÁSODRENDŰ NYOMATÉKAI HATVÁNYFÜGGVÉNY ALATTI TERÜLET Az origóból induló hatványfüggvények alatti terület esetén a másodrendű nyomatékok értéke (a koordinátatengelyekre!!!) a befoglaló téglalap adataiból egyszerűen meghatározható. ymax=b y y=xn x xmax=a SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék dx MECHANIKA I. Keresztmetszeti jellemzők 27

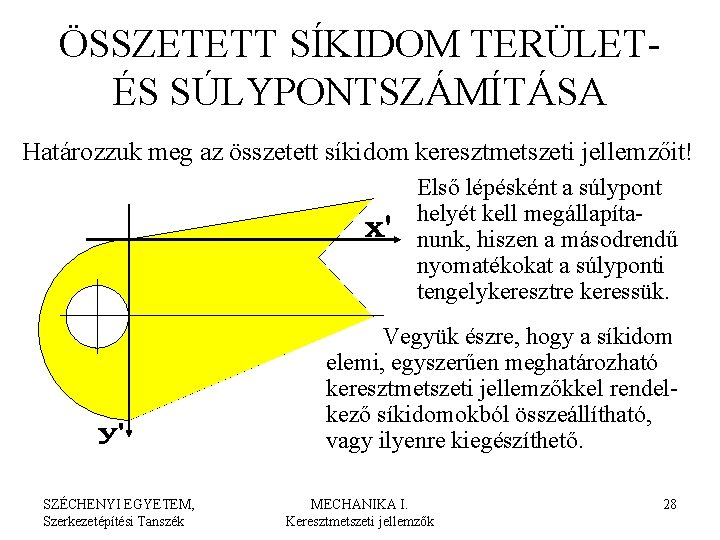
ÖSSZETETT SÍKIDOM TERÜLETÉS SÚLYPONTSZÁMÍTÁSA Határozzuk meg az összetett síkidom keresztmetszeti jellemzőit! Első lépésként a súlypont helyét kell megállapítanunk, hiszen a másodrendű nyomatékokat a súlyponti tengelykeresztre keressük. Vegyük észre, hogy a síkidom elemi, egyszerűen meghatározható keresztmetszeti jellemzőkkel rendelkező síkidomokból összeállítható, vagy ilyenre kiegészíthető. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék MECHANIKA I. Keresztmetszeti jellemzők 28

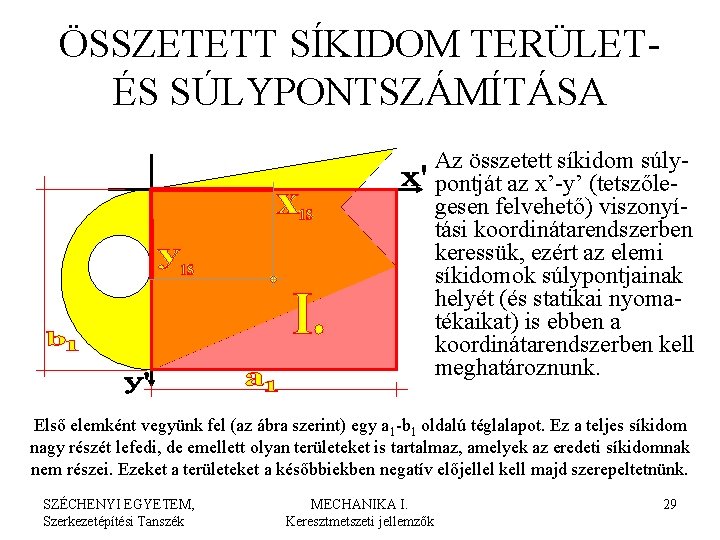
ÖSSZETETT SÍKIDOM TERÜLETÉS SÚLYPONTSZÁMÍTÁSA Az összetett síkidom súlypontját az x’-y’ (tetszőlegesen felvehető) viszonyítási koordinátarendszerben keressük, ezért az elemi síkidomok súlypontjainak helyét (és statikai nyomatékaikat) is ebben a koordinátarendszerben kell meghatároznunk. Első elemként vegyünk fel (az ábra szerint) egy a 1 -b 1 oldalú téglalapot. Ez a teljes síkidom nagy részét lefedi, de emellett olyan területeket is tartalmaz, amelyek az eredeti síkidomnak nem részei. Ezeket a területeket a későbbiekben negatív előjellel kell majd szerepeltetnünk. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék MECHANIKA I. Keresztmetszeti jellemzők 29

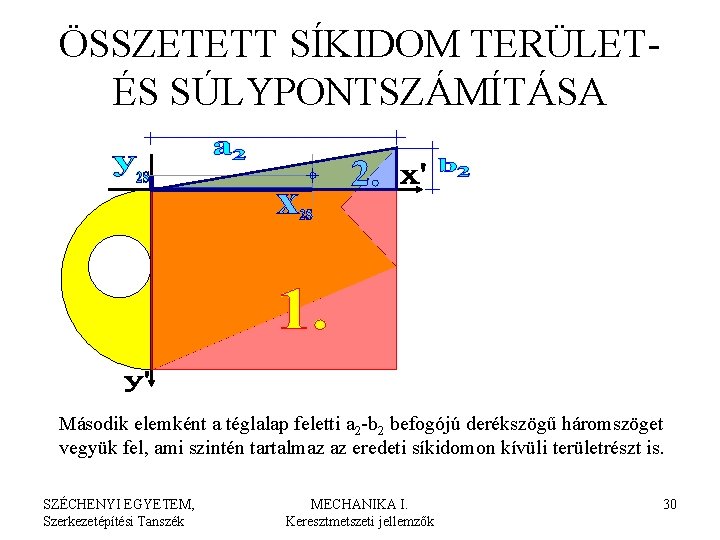
ÖSSZETETT SÍKIDOM TERÜLETÉS SÚLYPONTSZÁMÍTÁSA Második elemként a téglalap feletti a 2 -b 2 befogójú derékszögű háromszöget vegyük fel, ami szintén tartalmaz az eredeti síkidomon kívüli területrészt is. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék MECHANIKA I. Keresztmetszeti jellemzők 30

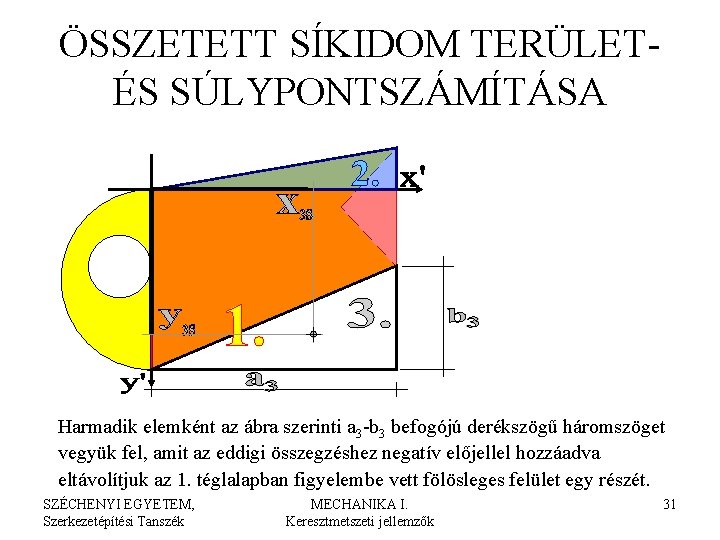
ÖSSZETETT SÍKIDOM TERÜLETÉS SÚLYPONTSZÁMÍTÁSA Harmadik elemként az ábra szerinti a 3 -b 3 befogójú derékszögű háromszöget vegyük fel, amit az eddigi összegzéshez negatív előjellel hozzáadva eltávolítjuk az 1. téglalapban figyelembe vett fölösleges felület egy részét. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék MECHANIKA I. Keresztmetszeti jellemzők 31

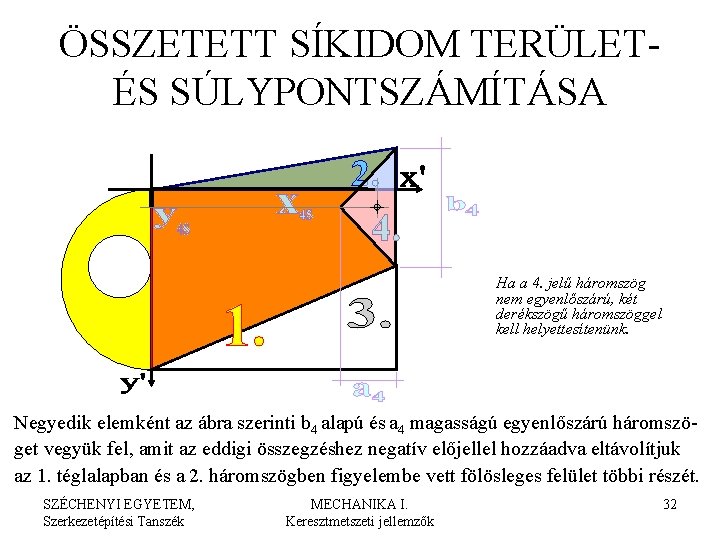
ÖSSZETETT SÍKIDOM TERÜLETÉS SÚLYPONTSZÁMÍTÁSA Ha a 4. jelű háromszög nem egyenlőszárú, két derékszögű háromszöggel kell helyettesítenünk. Negyedik elemként az ábra szerinti b 4 alapú és a 4 magasságú egyenlőszárú háromszöget vegyük fel, amit az eddigi összegzéshez negatív előjellel hozzáadva eltávolítjuk az 1. téglalapban és a 2. háromszögben figyelembe vett fölösleges felület többi részét. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék MECHANIKA I. Keresztmetszeti jellemzők 32

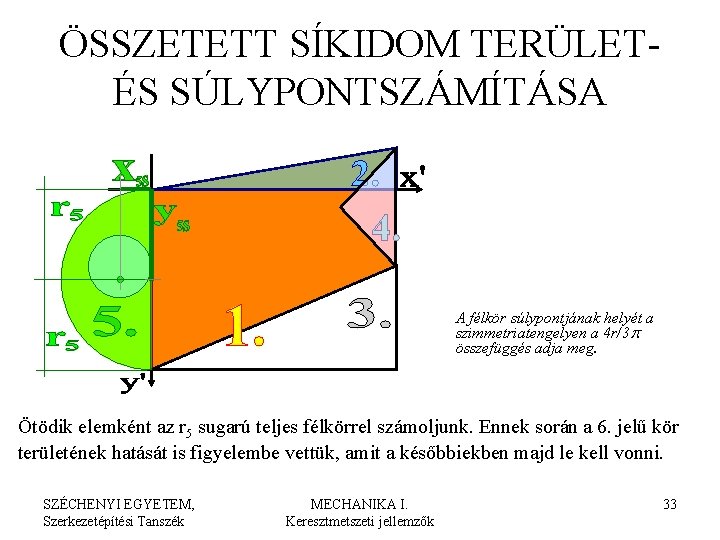
ÖSSZETETT SÍKIDOM TERÜLETÉS SÚLYPONTSZÁMÍTÁSA A félkör súlypontjának helyét a szimmetriatengelyen a 4 r/3 p összefüggés adja meg. Ötödik elemként az r 5 sugarú teljes félkörrel számoljunk. Ennek során a 6. jelű kör területének hatását is figyelembe vettük, amit a későbbiekben majd le kell vonni. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék MECHANIKA I. Keresztmetszeti jellemzők 33

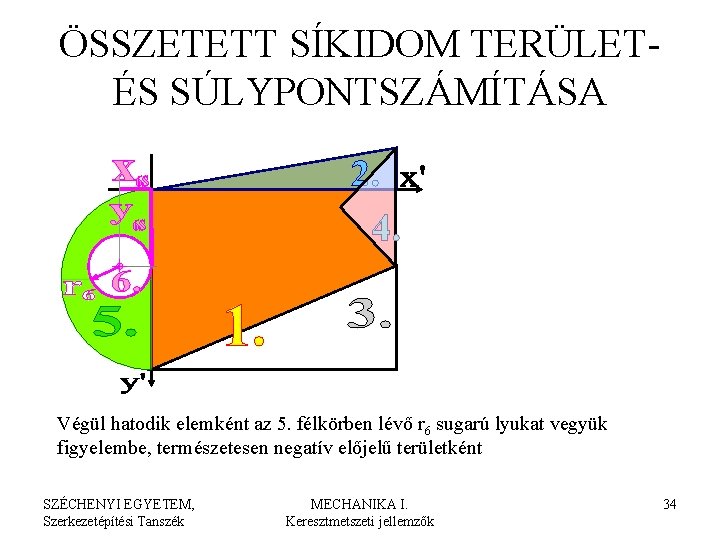
ÖSSZETETT SÍKIDOM TERÜLETÉS SÚLYPONTSZÁMÍTÁSA Végül hatodik elemként az 5. félkörben lévő r 6 sugarú lyukat vegyük figyelembe, természetesen negatív előjelű területként SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék MECHANIKA I. Keresztmetszeti jellemzők 34

ÖSSZETETT SÍKIDOM TERÜLETÉS SÚLYPONTSZÁMÍTÁSA JEL 1 2 3 4 5 6 A xi. S yi. S Sy Sx a 1×b 1 a 1/2 b 1/2 A 1×x 1 S A 1×y 1 S (a 2×b 2)/2 2 a 2/3 -b 2/3 A 2×x 2 S A 2×y 2 S (b 1 -b 3/3) A 3×x 3 S A 3×y 3 S -(a 4×b 4)/2 (a 1 -a 4/3) (-b 2+b 4/2) A 4×x 4 S A 4×y 4 S r 52 p/2 r 5 -4 r 5/3 p A 5×x 5 S A 5×y 5 S -r 62 p b 1 -b 3 - r 6 A 6×x 6 S A 6×y 6 S SSy SSx -(a 3×b 3)/2 2 a 3/3 SA SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék MECHANIKA I. Keresztmetszeti jellemzők 35

ÖSSZETETT SÍKIDOM TERÜLETÉS SÚLYPONTSZÁMÍTÁSA Természetesen más felbontás-kiegészítés is lehetséges, mint pl. a fenti ábra szerinti felbontás. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék MECHANIKA I. Keresztmetszeti jellemzők 36

A SÚLYPONTI TENGELYKERESZT ELFORDÍTÁSÁNAK HATÁSA Az eddigiekben megvizsgáltuk, hogyan lehet egy síkidom másodrendű nyomatékait a súlyponti tengelyekre előállítani. A STEINER tétel segítségével a tengely(ek) transzlációjának (párhuzamos eltolásának) hatását is figyelembe tudjuk venni. A továbbiakban azt nézzük meg, milyen változást okoz a tengelyek (súlypont körüli) elfordítása, rotációja. Ennek ismeretében (egy transzláció és egy rotáció összetételével) bármilyen állású tengelyre elő tudjuk állítani a síkidom másodrendű nyomatékait. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék MECHANIKA I. Keresztmetszeti jellemzők 37

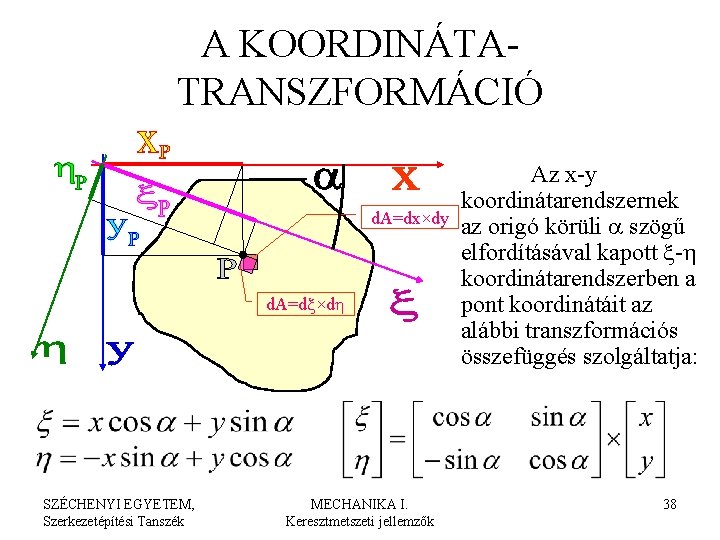
A KOORDINÁTATRANSZFORMÁCIÓ d. A=dx×dy d. A=dx×dh SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék MECHANIKA I. Keresztmetszeti jellemzők Az x-y koordinátarendszernek az origó körüli a szögű elfordításával kapott x-h koordinátarendszerben a pont koordinátáit az alábbi transzformációs összefüggés szolgáltatja: 38

A MÁSODRENDŰ NYOMATÉK AZ ELFORDÍTÁSI SZÖG FÜGGVÉNYÉBEN Az elfordított tengelyekre alkalmazva a másodrendű nyomatékok matematikai definícióját, és az abban szereplő új (x-h) változók helyére beírva az x-y koordináták transzformált összefüggését, az eredeti x-y koordináták és az elfordítási szög függvényében előállíthatók az elfordított tengelykeresztre érvényes másodrendű nyomatékok. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék MECHANIKA I. Keresztmetszeti jellemzők 39

A MÁSODRENDŰ NYOMATÉK AZ ELFORDÍTÁSI SZÖG FÜGGVÉNYÉBEN Az Jx-re kapott összefüggésben a sinacosa a sin(2 a) fele, így felmerül az ötlet, hogy nem lehet-e a Jx és Jy együtthatóit is a kétszeres szögfüggvényével felírni. adjunk hozzá a jelölt kifejezéshez 0 -t, a következő módon: SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék MECHANIKA I. Keresztmetszeti jellemzők 40

A MÁSODRENDŰ NYOMATÉK AZ ELFORDÍTÁSI SZÖG FÜGGVÉNYÉBEN Az Jx-ra kapott összefüggésben a sinacosa a sin(2 a) fele, így felmerül az ötlet, hogy nem lehet-e a Jx és Jy együtthatóit is a kétszeres szögfüggvényével felírni. adjunk hozzá a jelölt kifejezéshez 0 -t, a következő módon: SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék MECHANIKA I. Keresztmetszeti jellemzők 41

A MÁSODRENDŰ NYOMATÉK AZ ELFORDÍTÁSI SZÖG FÜGGVÉNYÉBEN Az elfordított tengelyekre alkalmazva a másodrendű nyomatékok matematikai definícióját, és az abban szereplő új (x-h) változók helyére beírva az x-y koordináták transzformált összefüggését, az eredeti x-y koordináták és az elfordítási szög függvényében előállíthatók az elfordított tengelykeresztre érvényes másodrendű nyomatékok. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék MECHANIKA I. Keresztmetszeti jellemzők 42

A MÁSODRENDŰ NYOMATÉK AZ ELFORDÍTÁSI SZÖG FÜGGVÉNYÉBEN Az Jh-re kapott összefüggésben a sinacosa a sin(2 a) fele, így felmerül az ötlet, hogy nem lehet-e a Jx és Jy együtthatóit is a kétszeres szögfüggvényével felírni. adjunk hozzá a jelölt kifejezéshez 0 -t, a következő módon: SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék MECHANIKA I. Keresztmetszeti jellemzők 43

A MÁSODRENDŰ NYOMATÉK AZ ELFORDÍTÁSI SZÖG FÜGGVÉNYÉBEN Az Jx-ra kapott összefüggésben a sinacosa a sin(2 a) fele, így felmerül az ötlet, hogy nem lehet-e a Jx és Jy együtthatóit is a kétszeres szögfüggvényével felírni. adjunk hozzá a jelölt kifejezéshez 0 -t, a következő módon: SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék MECHANIKA I. Keresztmetszeti jellemzők 44

A MÁSODRENDŰ NYOMATÉK AZ ELFORDÍTÁSI SZÖG FÜGGVÉNYÉBEN Mindezek alapján a x és h tengelyre vonatkozó tehetetlenségi nyomaték a következő egyszerű(bb) alakban írható fel: SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék MECHANIKA I. Keresztmetszeti jellemzők 45

A MÁSODRENDŰ NYOMATÉK AZ ELFORDÍTÁSI SZÖG FÜGGVÉNYÉBEN A centrifugális nyomaték előállítása: SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék MECHANIKA I. Keresztmetszeti jellemzők 46

A TEHETETLENSÉGI FŐIRÁNYOK A x-h koordinátarendszert az origó körül forgatva minden állásban értelmezhetők és előállíthatók a síkidom másodrendű nyomatékai, azaz az Jx, az Jh és a Cxh az a elfordítási szögnek folytonos függvénye. Ugyanakkor 360 fokos elfordítás után a koordinátarendszer az eredeti helyzetbe kerül vissza, tehát az Jx, az Jh és a Cxh az a elfordítási szögnek periodikus függvénye. Ha pedig egy függvény egyidejűleg folytonos és periodikus, akkor korlátos is. Ha pedig a tehetetlenségi nyomatékok elfordítási szög szerinti függvénye korlátos, akkor meg lehet (és meg is kell!) határoznunk a szélső értékeit, és az azokhoz tartozó elfordítási szögek értékeit. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék MECHANIKA I. Keresztmetszeti jellemzők 47

A FŐTEHETETLENSÉGI NYOMATÉKOK Az Jx összefüggésére alkalmazva a d/da differenciáloperátort keressük a derivált függvény zérushelyét. Az átalakítások eredményén látható, hogy az (egy előjelváltástól és egy 2 -es szorzótól eltekintve) a Cxh képletével azonos, azaz a tehetetlenségi nyomaték a tengelykereszt forgatása során abban a tengelyállásban veszi fel a szélső értékeit, amelyben a tengelykeresztre felírható centrifugális nyomaték értéke zérus. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék MECHANIKA I. Keresztmetszeti jellemzők 48

A FŐTEHETETLENSÉGI NYOMATÉKOK 1. 2. A főtehetetlenségi nyomatékok számítási képletei és az inerciák alakulása a különböző elforgatási szögű tengelyekre SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék MECHANIKA I. Keresztmetszeti jellemzők 49

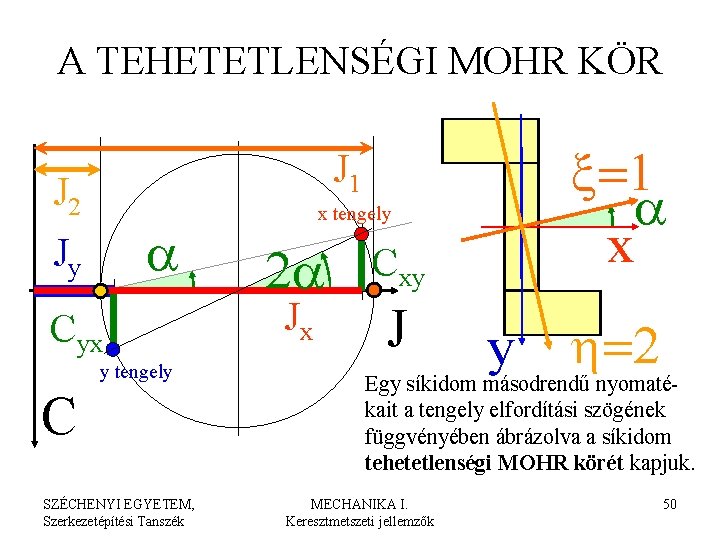
A TEHETETLENSÉGI MOHR KÖR J 1 J 2 a Jy Cyx y tengely C SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék x tengely 2 a Jx Cxy x=1 a x J h=2 y Egy síkidom másodrendű nyomatékait a tengely elfordítási szögének függvényében ábrázolva a síkidom tehetetlenségi MOHR körét kapjuk. MECHANIKA I. Keresztmetszeti jellemzők 50

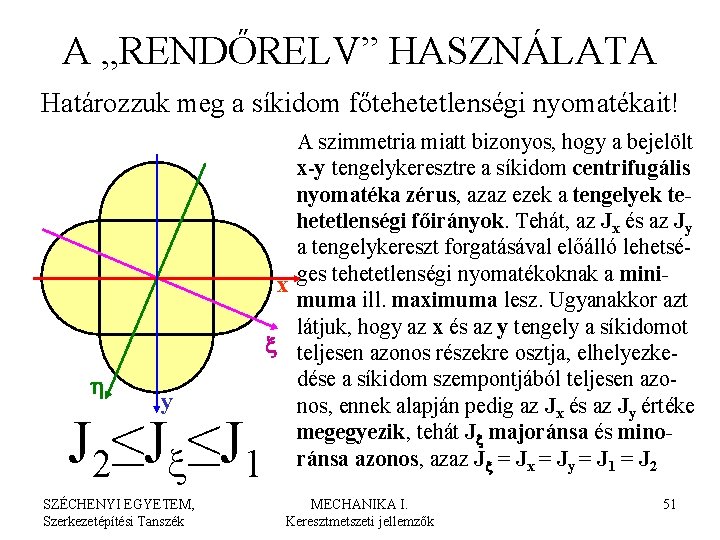
A „RENDŐRELV” HASZNÁLATA Határozzuk meg a síkidom főtehetetlenségi nyomatékait! h y J 2≤Jx≤J 1 SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék A szimmetria miatt bizonyos, hogy a bejelölt x-y tengelykeresztre a síkidom centrifugális nyomatéka zérus, azaz ezek a tengelyek tehetetlenségi főirányok. Tehát, az Jx és az Jy a tengelykereszt forgatásával előálló lehetséx ges tehetetlenségi nyomatékoknak a minimuma ill. maximuma lesz. Ugyanakkor azt látjuk, hogy az x és az y tengely a síkidomot x teljesen azonos részekre osztja, elhelyezkedése a síkidom szempontjából teljesen azonos, ennek alapján pedig az Jx és az Jy értéke megegyezik, tehát Jx majoránsa és minoránsa azonos, azaz Jx = Jy = J 1 = J 2 MECHANIKA I. Keresztmetszeti jellemzők 51

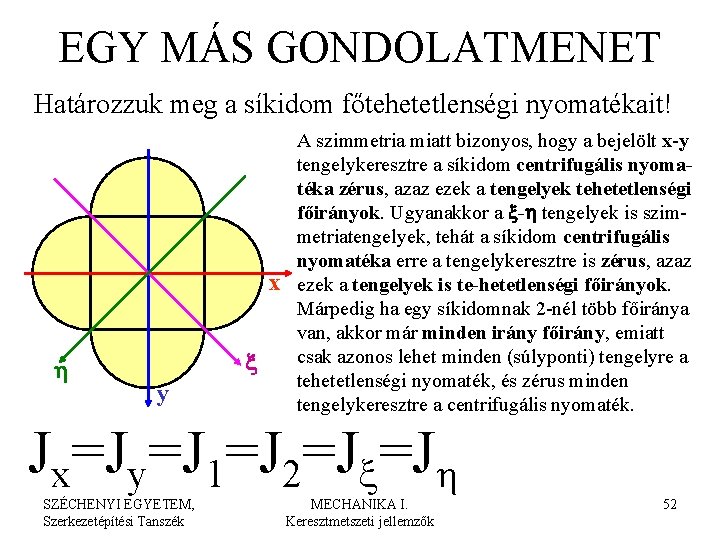
EGY MÁS GONDOLATMENET Határozzuk meg a síkidom főtehetetlenségi nyomatékait! x h x y A szimmetria miatt bizonyos, hogy a bejelölt x-y tengelykeresztre a síkidom centrifugális nyomatéka zérus, azaz ezek a tengelyek tehetetlenségi főirányok. Ugyanakkor a x-h tengelyek is szimmetriatengelyek, tehát a síkidom centrifugális nyomatéka erre a tengelykeresztre is zérus, azaz ezek a tengelyek is te-hetetlenségi főirányok. Márpedig ha egy síkidomnak 2 -nél több főiránya van, akkor már minden irány főirány, emiatt csak azonos lehet minden (súlyponti) tengelyre a tehetetlenségi nyomaték, és zérus minden tengelykeresztre a centrifugális nyomaték. Jx=Jy=J 1=J 2=Jx=Jh SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék MECHANIKA I. Keresztmetszeti jellemzők 52