Mechanics of Materials Internal Forces Distributed Loads I

Mechanics of Materials Internal Forces – Distributed Loads ‘I don't care to belong to a club that accepts people like me as members. ’ Groucho Marx

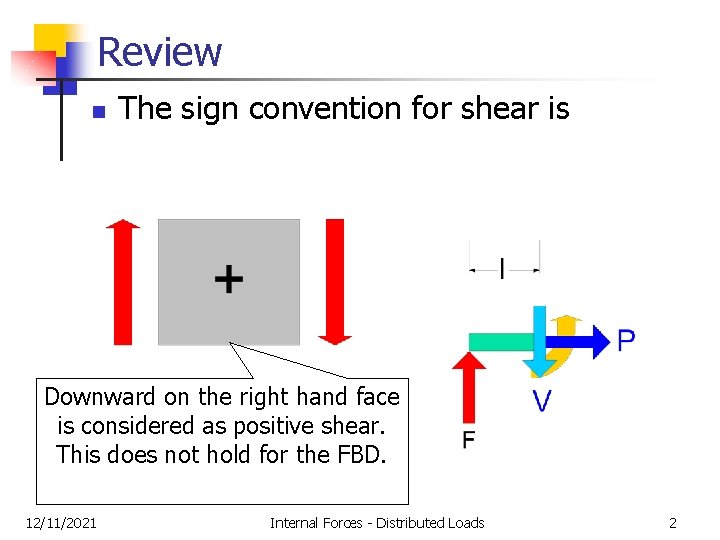
Review n The sign convention for shear is Downward on the right hand face is considered as positive shear. This does not hold for the FBD. 12/11/2021 Internal Forces - Distributed Loads 2

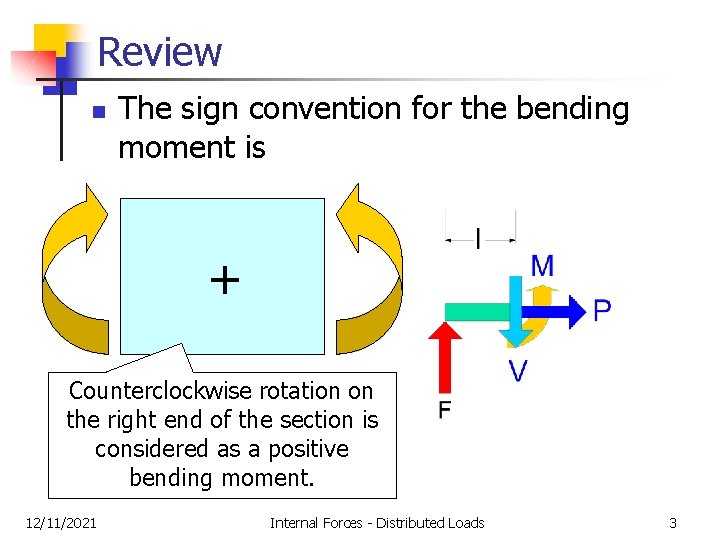
Review n The sign convention for the bending moment is + Counterclockwise rotation on the right end of the section is considered as a positive bending moment. 12/11/2021 Internal Forces - Distributed Loads 3

Review n A general heuristic for finding the internal forces and moments at a point in a simple beam n n n 12/11/2021 Choose one end of the beam as the reference Convert all the distributed loads that act on the beam into forces Solve for the reaction at the reference end of the beam Internal Forces - Distributed Loads 4

Review n A general heuristic for finding the internal forces and moments at a point in a simple beam n n n 12/11/2021 Draw a new FBD of the beam section under consideration including all distributed loads as distributed loads Draw the shear and axial forces, and the bending moment at the cut surface following our sign conventions Solve for these three components using the equations of equilibrium Internal Forces - Distributed Loads 5

Distributed Loads n n 12/11/2021 There is one point that we need to make in determining the internal forces When we have a distributed load that spans the point where we want to calculate the internal forces, we need to be careful that we only include that part of the distributed load which is on the section under consideration. Internal Forces - Distributed Loads 6

Distributed Loads n 12/11/2021 The is best illustrated by working a simple example problem. Internal Forces - Distributed Loads 7

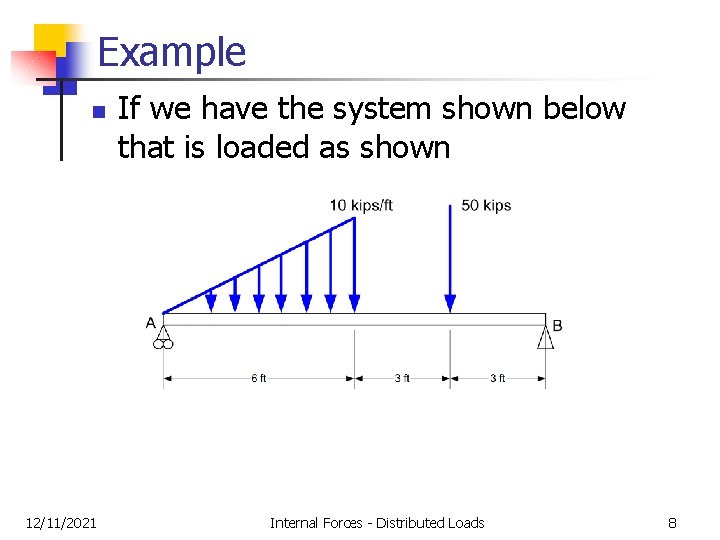
Example n 12/11/2021 If we have the system shown below that is loaded as shown Internal Forces - Distributed Loads 8

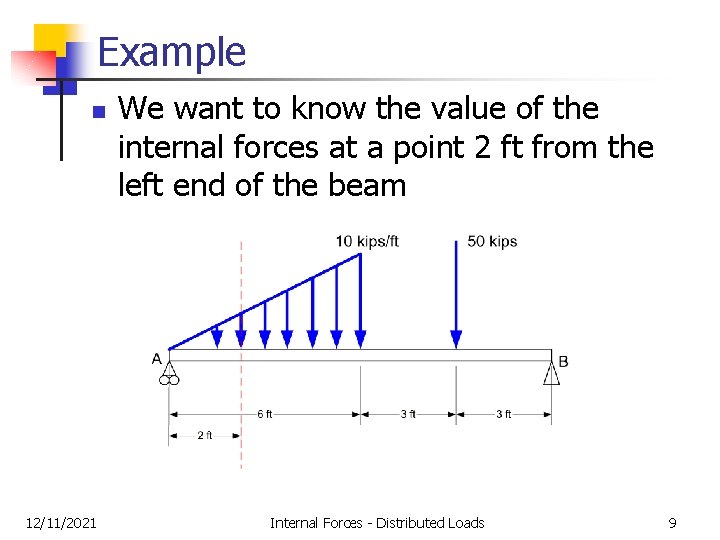
Example n 12/11/2021 We want to know the value of the internal forces at a point 2 ft from the left end of the beam Internal Forces - Distributed Loads 9

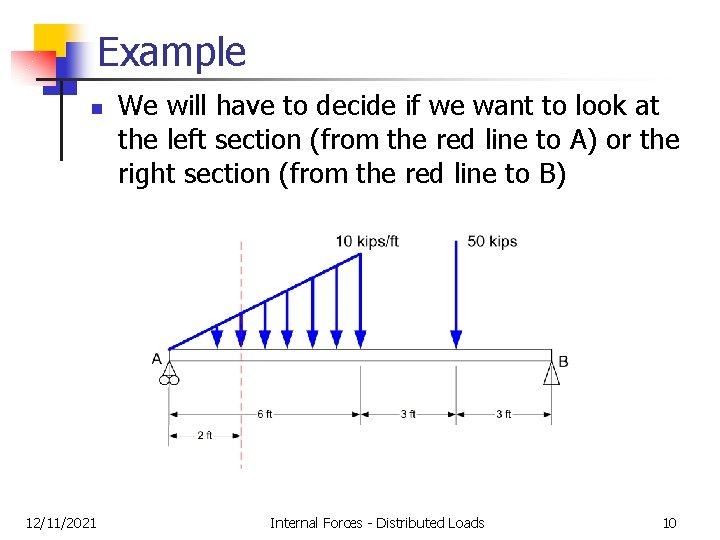
Example n 12/11/2021 We will have to decide if we want to look at the left section (from the red line to A) or the right section (from the red line to B) Internal Forces - Distributed Loads 10

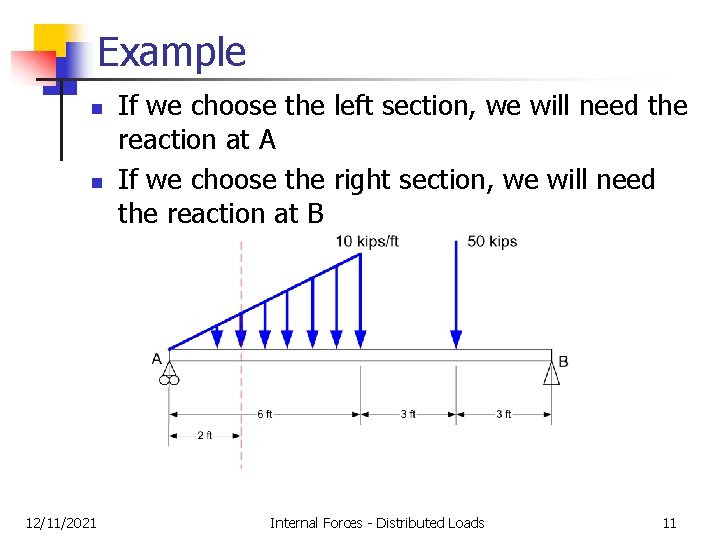
Example n n 12/11/2021 If we choose the left section, we will need the reaction at A If we choose the right section, we will need the reaction at B Internal Forces - Distributed Loads 11

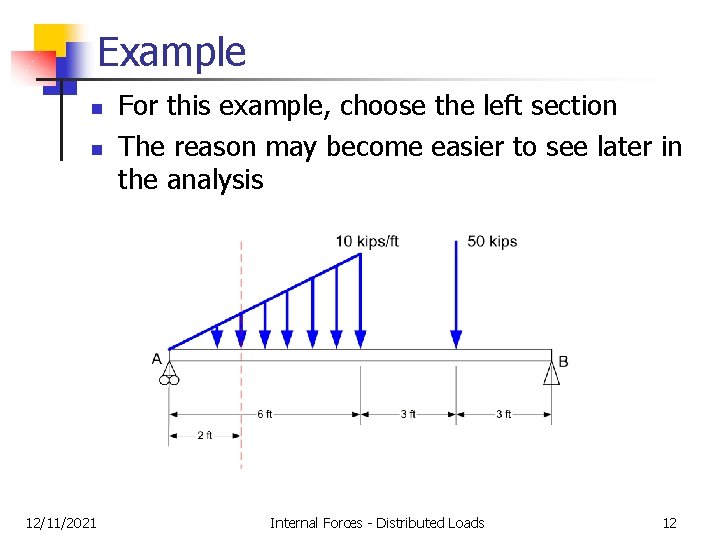
Example n n 12/11/2021 For this example, choose the left section The reason may become easier to see later in the analysis Internal Forces - Distributed Loads 12

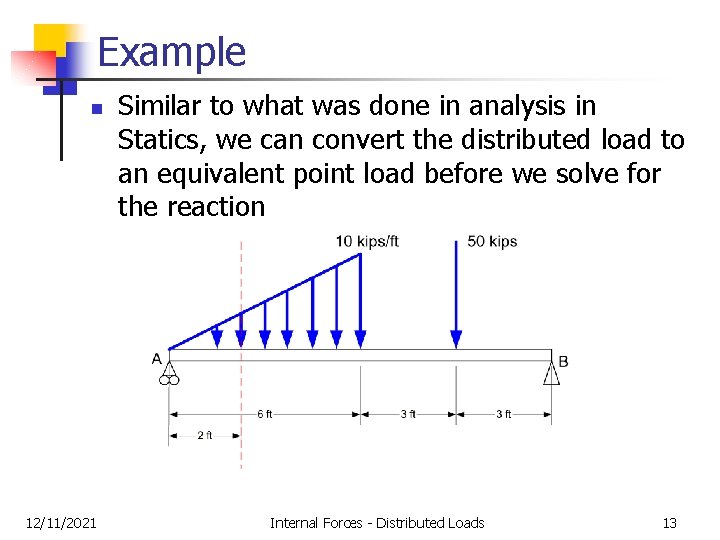
Example n 12/11/2021 Similar to what was done in analysis in Statics, we can convert the distributed load to an equivalent point load before we solve for the reaction Internal Forces - Distributed Loads 13

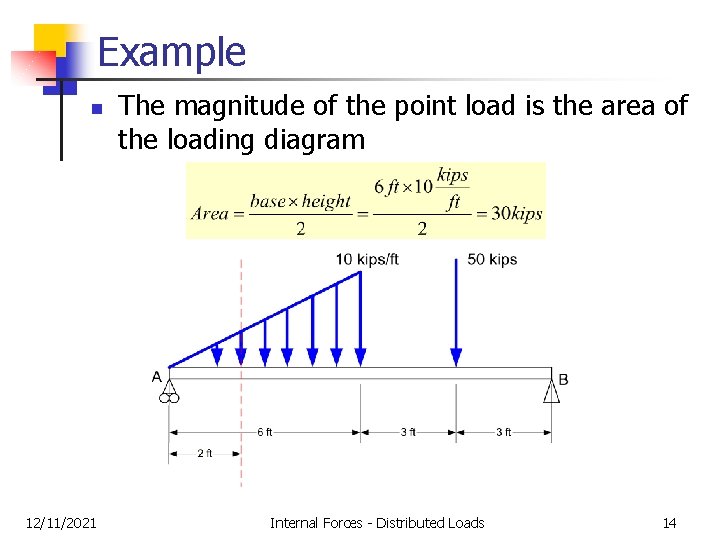
Example n 12/11/2021 The magnitude of the point load is the area of the loading diagram Internal Forces - Distributed Loads 14

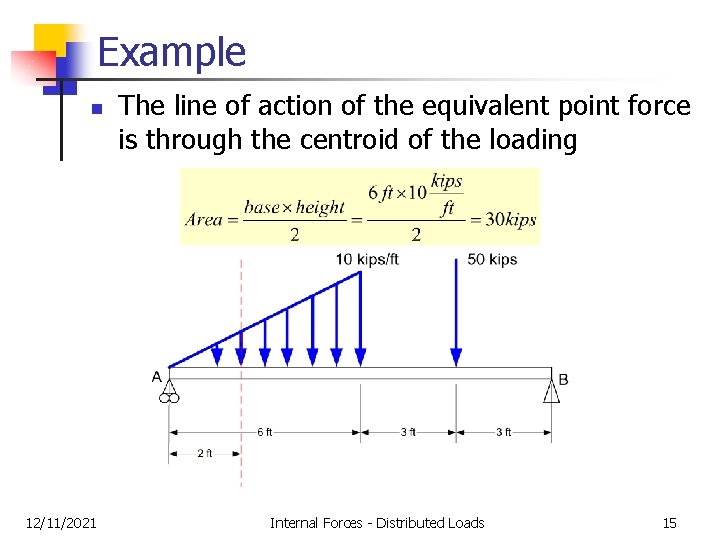
Example n 12/11/2021 The line of action of the equivalent point force is through the centroid of the loading Internal Forces - Distributed Loads 15

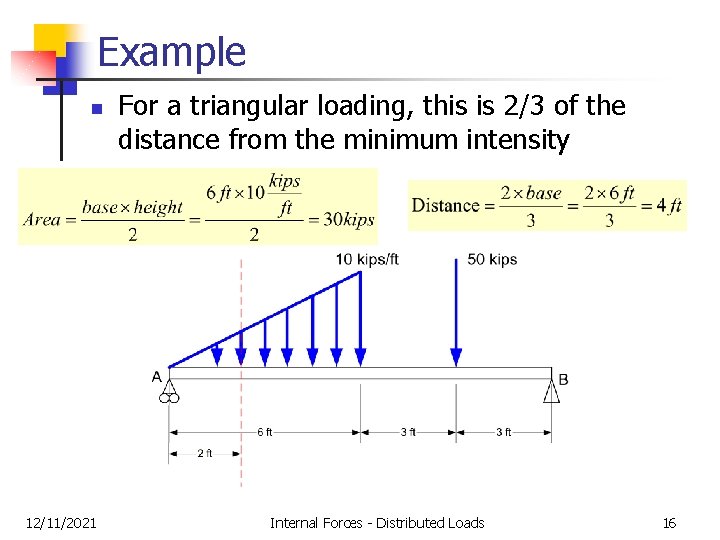
Example n 12/11/2021 For a triangular loading, this is 2/3 of the distance from the minimum intensity Internal Forces - Distributed Loads 16

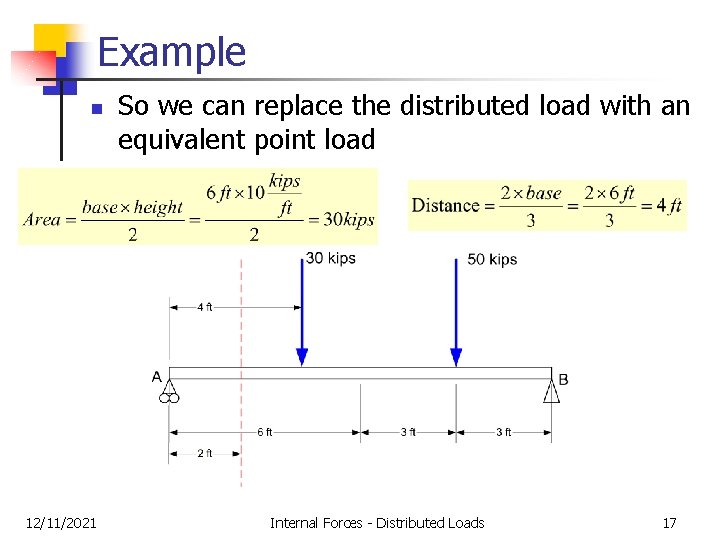
Example n 12/11/2021 So we can replace the distributed load with an equivalent point load Internal Forces - Distributed Loads 17

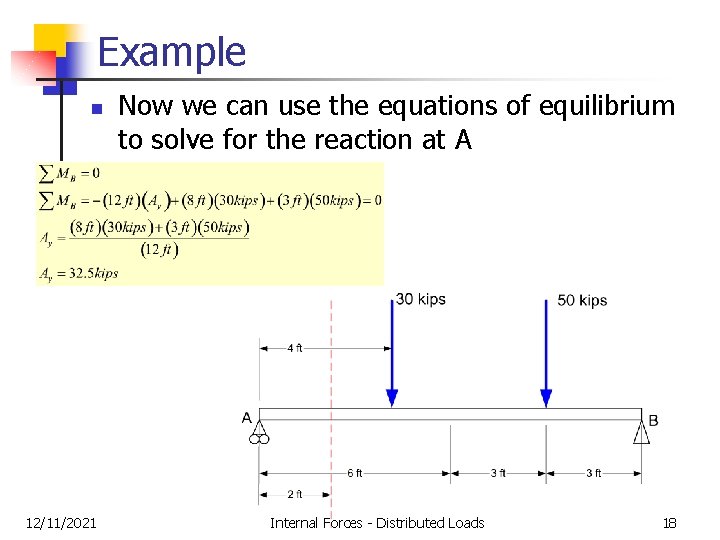
Example n 12/11/2021 Now we can use the equations of equilibrium to solve for the reaction at A Internal Forces - Distributed Loads 18

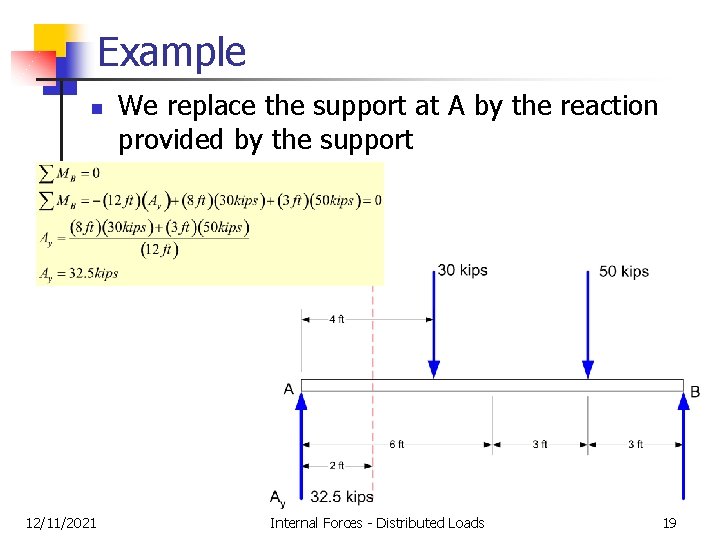
Example n 12/11/2021 We replace the support at A by the reaction provided by the support Internal Forces - Distributed Loads 19

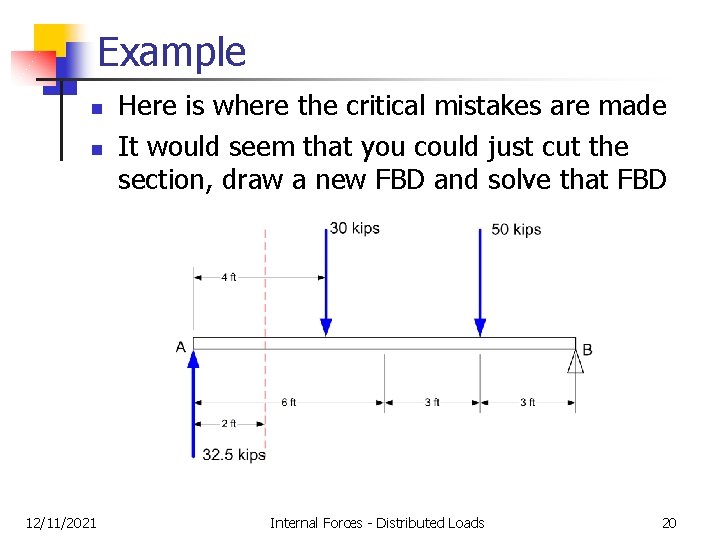
Example n n 12/11/2021 Here is where the critical mistakes are made It would seem that you could just cut the section, draw a new FBD and solve that FBD Internal Forces - Distributed Loads 20

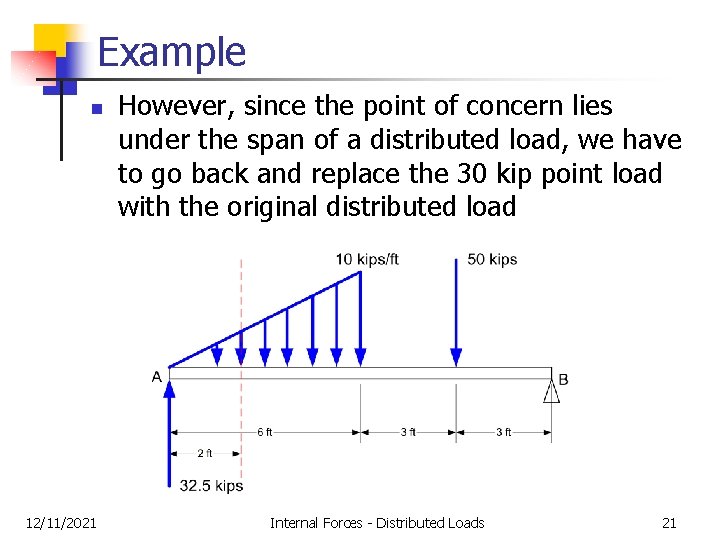
Example n 12/11/2021 However, since the point of concern lies under the span of a distributed load, we have to go back and replace the 30 kip point load with the original distributed load Internal Forces - Distributed Loads 21

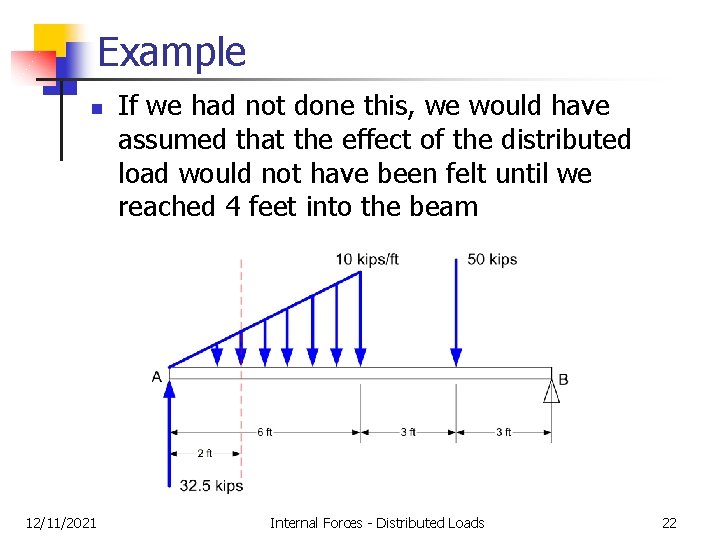
Example n 12/11/2021 If we had not done this, we would have assumed that the effect of the distributed load would not have been felt until we reached 4 feet into the beam Internal Forces - Distributed Loads 22

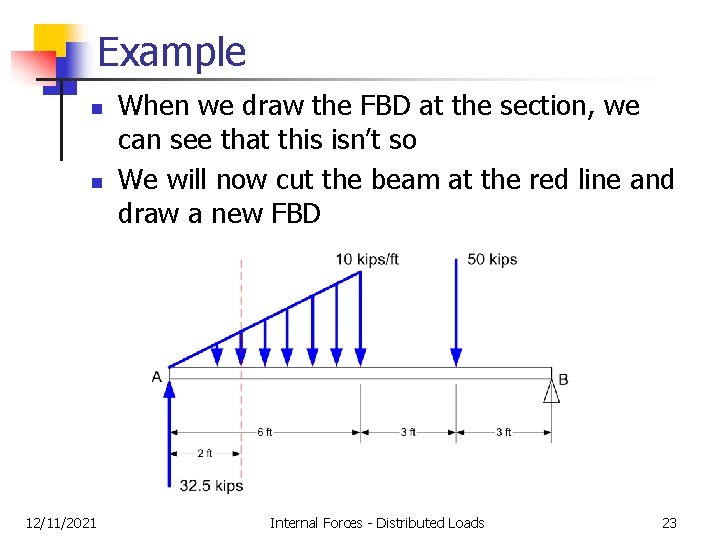
Example n n 12/11/2021 When we draw the FBD at the section, we can see that this isn’t so We will now cut the beam at the red line and draw a new FBD Internal Forces - Distributed Loads 23

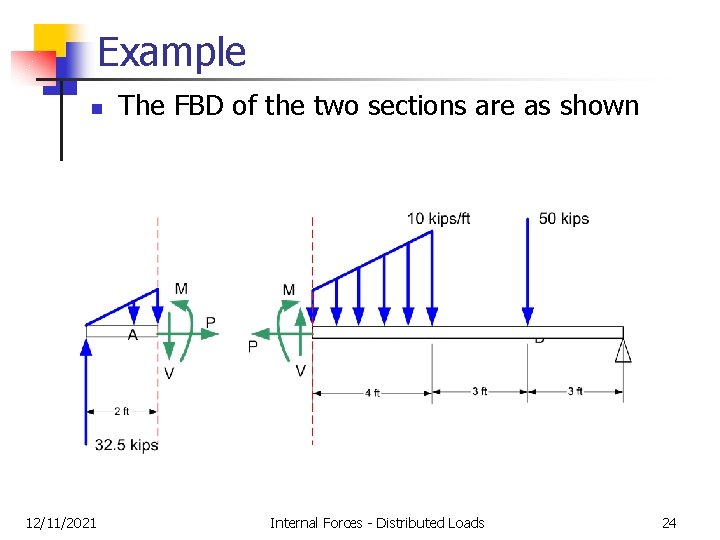
Example n 12/11/2021 The FBD of the two sections are as shown Internal Forces - Distributed Loads 24

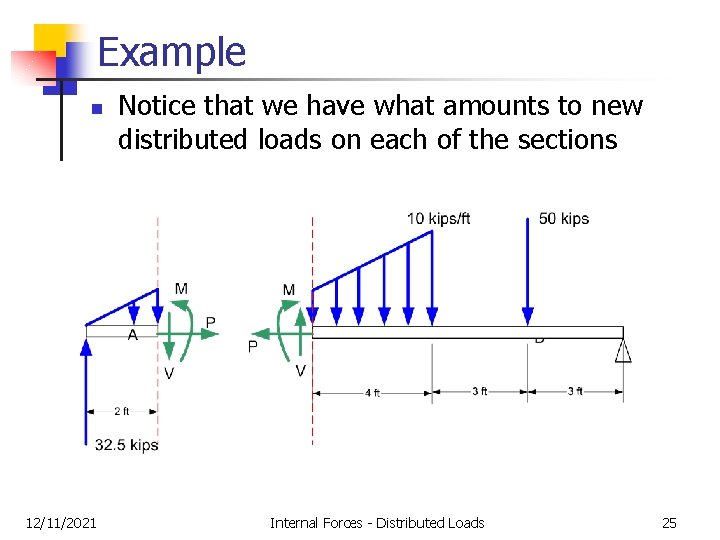
Example n 12/11/2021 Notice that we have what amounts to new distributed loads on each of the sections Internal Forces - Distributed Loads 25

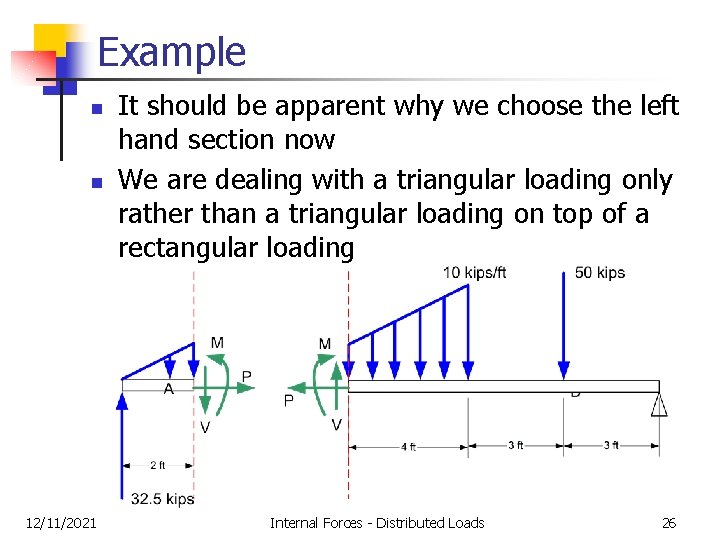
Example n n 12/11/2021 It should be apparent why we choose the left hand section now We are dealing with a triangular loading only rather than a triangular loading on top of a rectangular loading Internal Forces - Distributed Loads 26

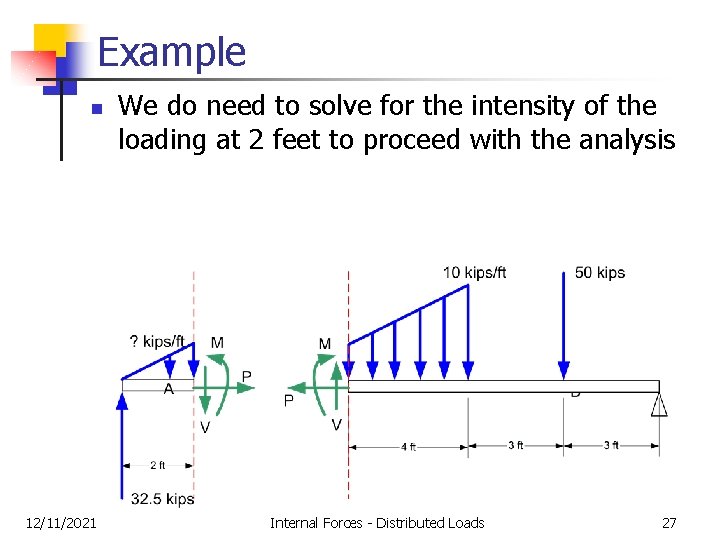
Example n 12/11/2021 We do need to solve for the intensity of the loading at 2 feet to proceed with the analysis Internal Forces - Distributed Loads 27

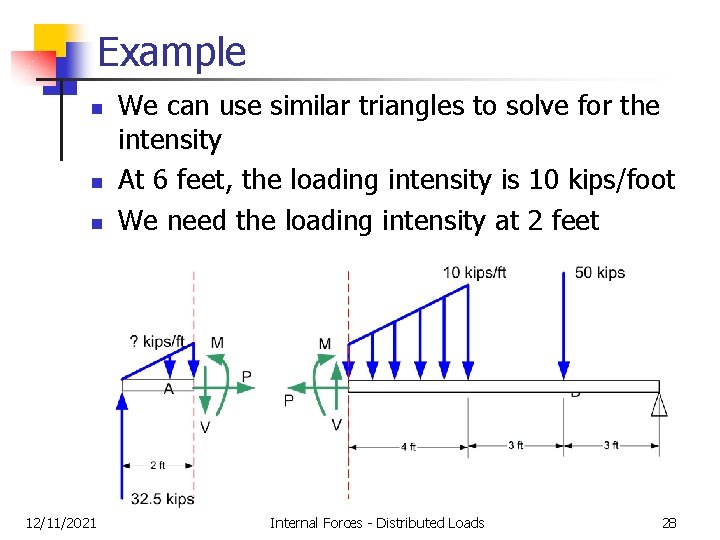
Example n n n 12/11/2021 We can use similar triangles to solve for the intensity At 6 feet, the loading intensity is 10 kips/foot We need the loading intensity at 2 feet Internal Forces - Distributed Loads 28

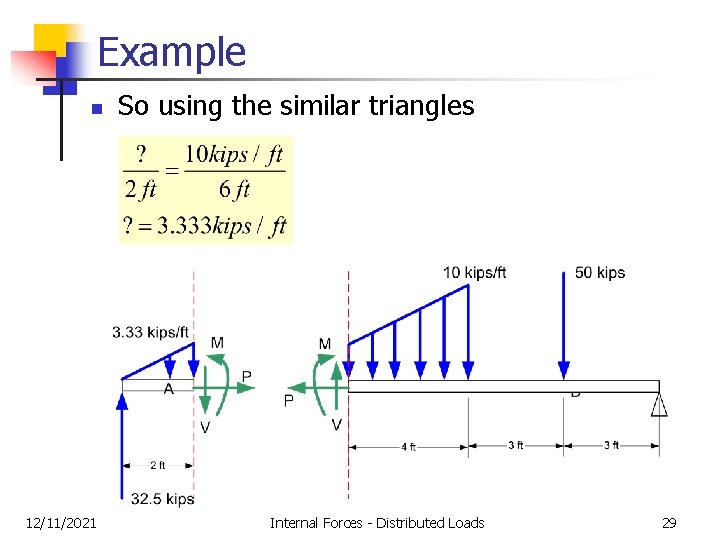
Example n 12/11/2021 So using the similar triangles Internal Forces - Distributed Loads 29

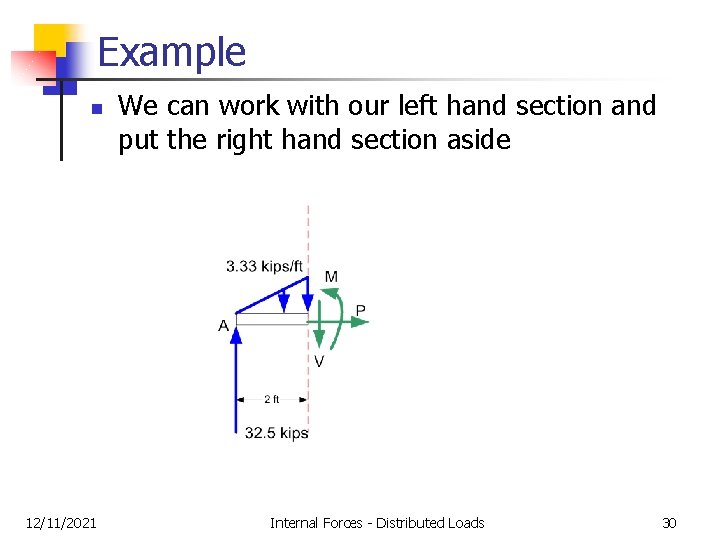
Example n 12/11/2021 We can work with our left hand section and put the right hand section aside Internal Forces - Distributed Loads 30

Example n 12/11/2021 I have assumed that the shear, the axial force, and the bending moment are all positive Internal Forces - Distributed Loads 31

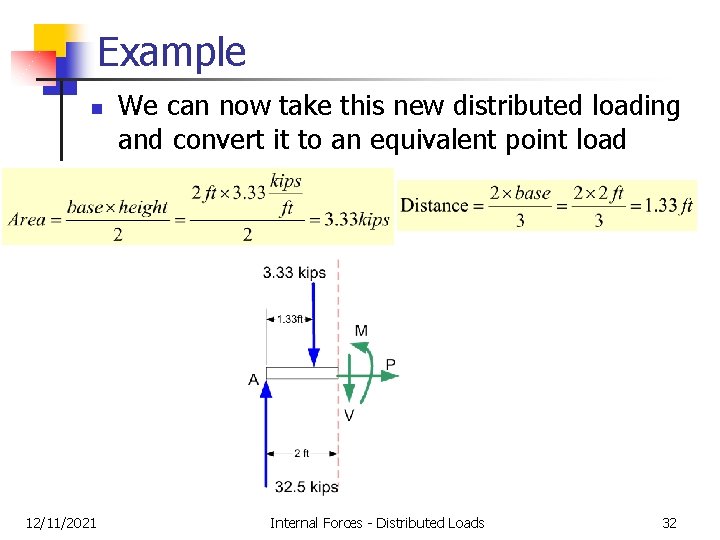
Example n 12/11/2021 We can now take this new distributed loading and convert it to an equivalent point load Internal Forces - Distributed Loads 32

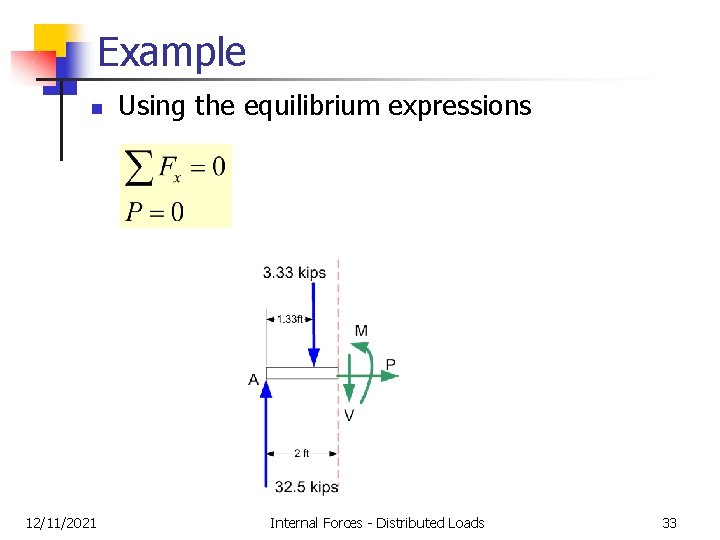
Example n 12/11/2021 Using the equilibrium expressions Internal Forces - Distributed Loads 33

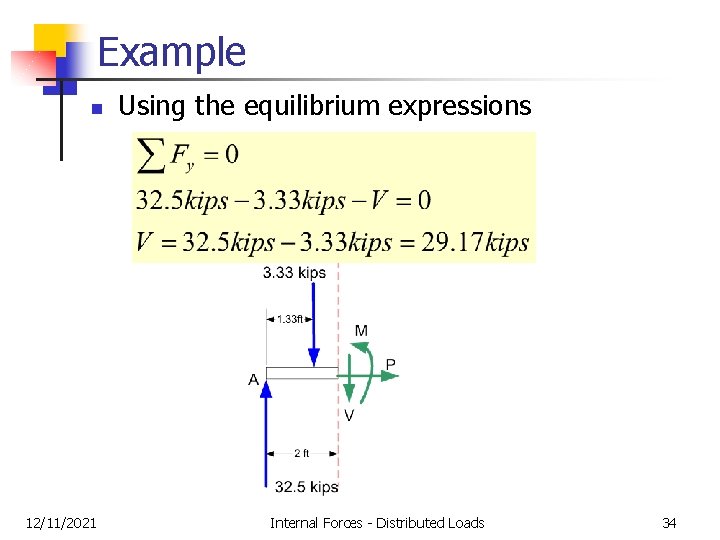
Example n 12/11/2021 Using the equilibrium expressions Internal Forces - Distributed Loads 34

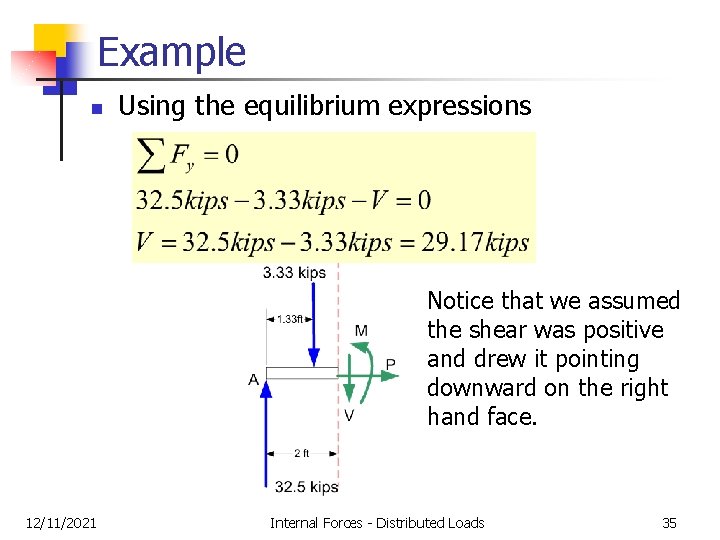
Example n Using the equilibrium expressions Notice that we assumed the shear was positive and drew it pointing downward on the right hand face. 12/11/2021 Internal Forces - Distributed Loads 35

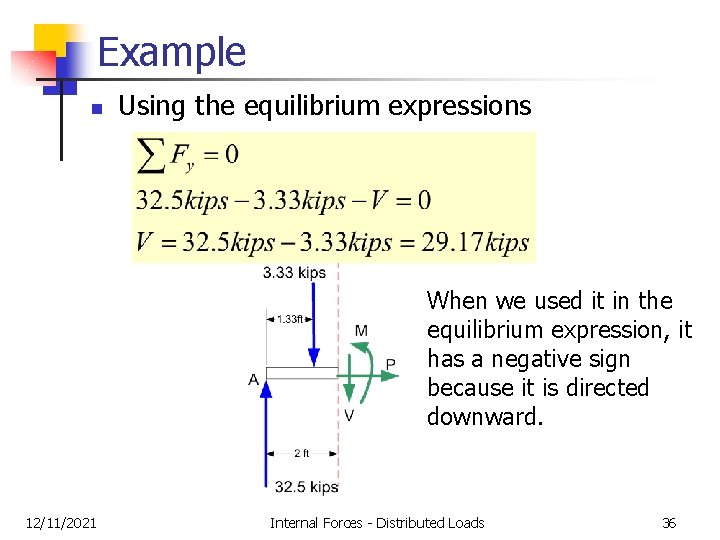
Example n Using the equilibrium expressions When we used it in the equilibrium expression, it has a negative sign because it is directed downward. 12/11/2021 Internal Forces - Distributed Loads 36

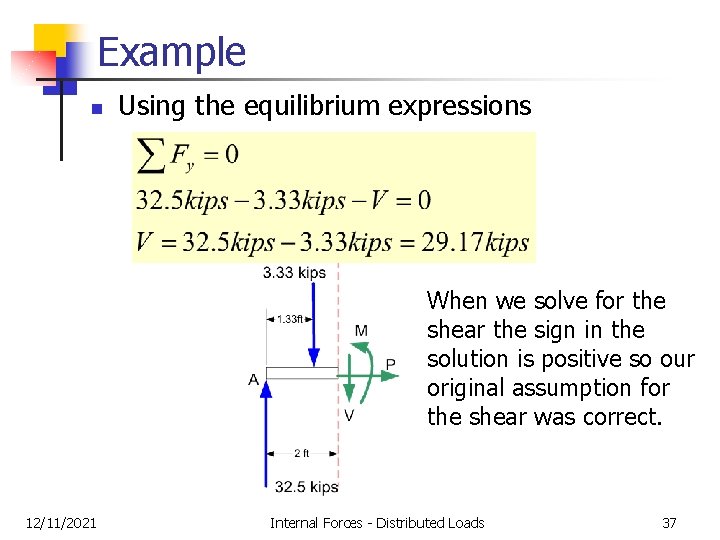
Example n Using the equilibrium expressions When we solve for the shear the sign in the solution is positive so our original assumption for the shear was correct. 12/11/2021 Internal Forces - Distributed Loads 37

Example n 12/11/2021 To solve for the bending moment, we choose a moment center and solve Internal Forces - Distributed Loads 38

Example n 12/11/2021 If you go back now and look at what would have happened if we had not reconsidered the distributed load acting on the section you can see that we would have overstated the shear and understated the moment Internal Forces - Distributed Loads 39

A Final Note n n 12/11/2021 When dealing with a system which has distributed loads acting on it take care when you want to calculate the internal forces on any point within the area covered by the distributed load When dealing with points that are not under the distributed loading, you can treat all the distributed loadings as equivalent point loads Internal Forces - Distributed Loads 40

Homework n 12/11/2021 7 -1. 13, 7 -1. 16, 7 - 1. 20 Internal Forces - Distributed Loads 41