Mechanics Molecular Kinetic Theory Contents Mechanics n Molecular

















- Slides: 25

Mechanics & Molecular Kinetic Theory

Contents Mechanics n Molecular Kinetic Theory n

Mechanics n Linear Motion: speed (m/s) = distance (m) time(s) velocity (m/s) = displacement (m) time (s) acceleration (m/s 2) = change in speed (m/s) time taken (s)

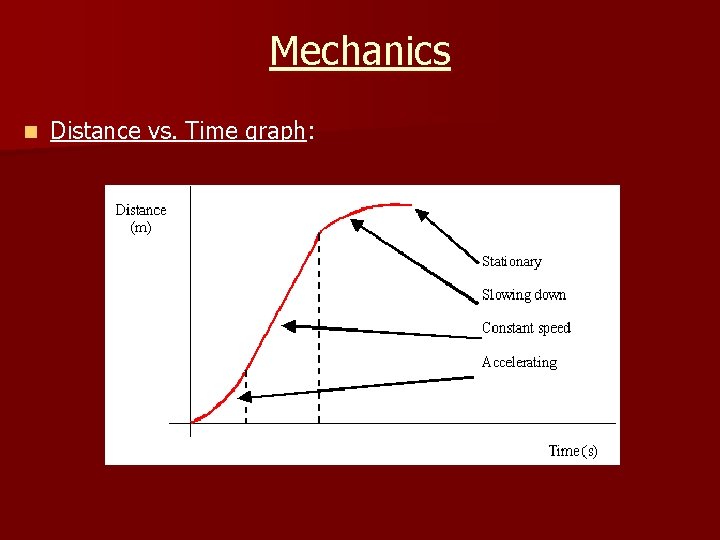
Mechanics n Distance vs. Time graph:

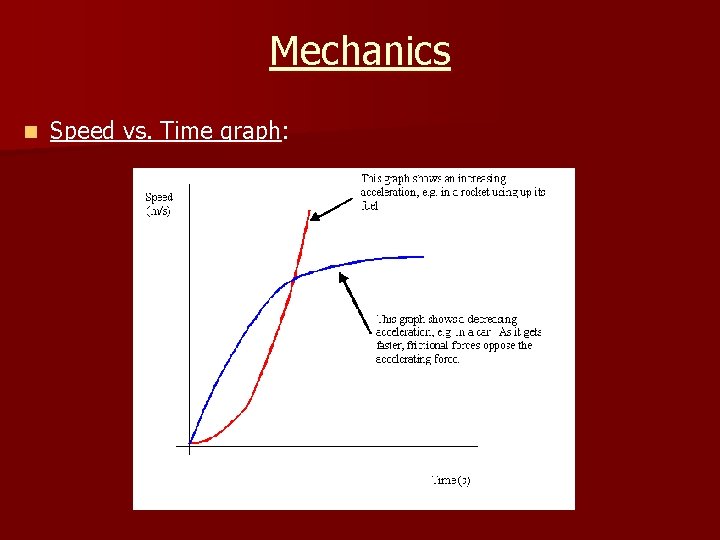
Mechanics n Speed vs. Time graph:

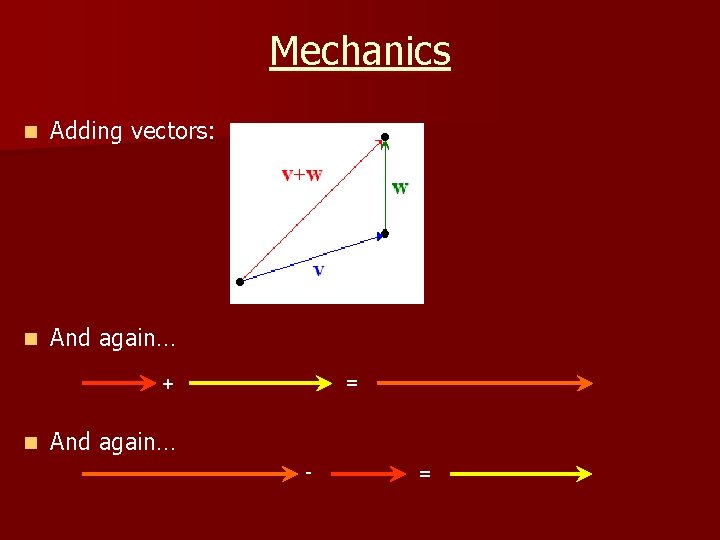
Mechanics n Forces and Vectors: n Examples: - scalar = speed - vector = velocity (1 quantity… no direction) (2 quantities… speed & direction) n Other vector quantities: - displacement - momentum - force n Vectors can be added to produce a resultant quantity

Mechanics n Adding vectors: n And again… = + n And again… - =

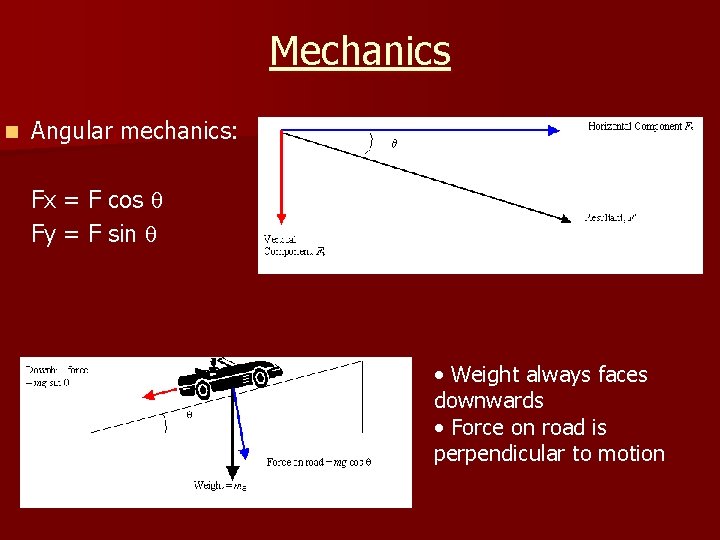
Mechanics n Angular mechanics: Fx = F cos Fy = F sin • Weight always faces downwards • Force on road is perpendicular to motion

Mechanics n Projectiles: - an object upon which the only force acting is gravity e. g. bullet - once projected, its motion depends on its inertia Initial velocity vectors: Vx = Vcos Vy = Vsin Flight time: t = Viy/g Displacement: X = Vxt Max. height: Y = Viyt + ½gt 2

Mechanics Moments: have a direction (clockwise or anti-clockwise) Moment = force × perpendicular distance (Nm) = (N) x (m) n clockwise moment = anti-clockwise moment (equilibrium) - this is used to find the centre of gravity n Work = Force × distance moved in the direction of the force (Nm or J) = (N) x (m) n - When work is done, energy is transferred - Energy comes in many forms; some kinds of energy can be stored, while others cannot - Energy is always conserved

Mechanics n Power: rate at which energy is transferred power (W) = energy (J) / time (secs) energy (work done) = force x distance So… power = (force x distance) / time power = force x speed P = Fv (d/t = speed)

Mechanics n Energy: the ability to do work. When work is done, energy is transferred - Some kinds of energy can be stored, while others cannot - Energy in a system is always conserved n Potential Energy: potential energy = weight × distance moved against gravity (Nm) = (N) x (m) n Kinetic Energy: kinetic energy = ½ mass x velocity 2 (J) = (kg) x (m/s 2)

Heat Capacity n Heat capacity (c): quantity of heat required to raise the temperature of a unit mass by 1°K Heat flow = m (J) = (kg) × c × delta T × (Jkg-1 K-1) × (K) Q = mc delta n specific latent heat: energy to change the state of a unit mass of liquid without a temperature change - fusion, or melting - vaporisation, or boiling delta Q = ml

Newton’s Laws n Newton’s 1 st Law: An object continues in its state of rest or uniform motion in a straight line, unless it has an external force acting on it n Newton’s 2 nd Law: Rate of change of momentum is proportional to the total force acting on a body, and occurs in the direction of the force F = ma n Newton’s 3 rd Law: If body A exerts a force on body B, body B must exert an equal and opposite force on body A

Collisions n Conservation of Momentum: Total momentum before = total momentum after Mu 1 + mu 2 = Mv 1 + mv 2 n Conservation of Energy: Total energy before = total energy after ½Mu 12 + ½mu 22 = ½Mv 12 + ½mv 22 n Elastic collisions: zero energy loss Impulse = Force x time (Ns) = (N) x (secs)

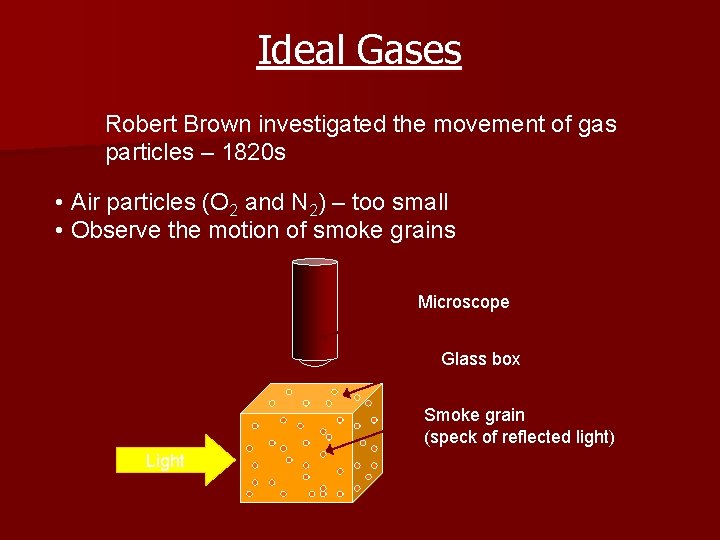
Ideal Gases Robert Brown investigated the movement of gas particles – 1820 s • Air particles (O 2 and N 2) – too small • Observe the motion of smoke grains Microscope Glass box Smoke grain (speck of reflected light) Light

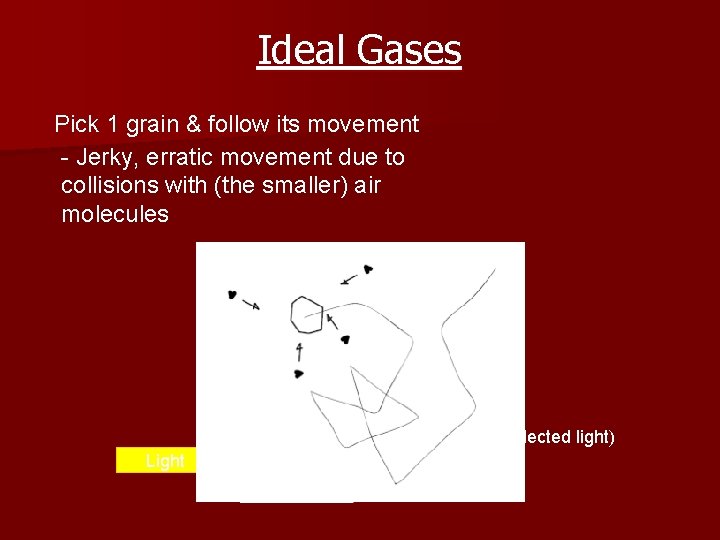
Ideal Gases Pick 1 grain & follow its movement - Jerky, erratic movement due to collisions with (the smaller) air molecules Microscope Glass box Smoke grain (speck of reflected light) Light

Ideal Gases STP = standard temperature and pressure T = 273 K, p = 1 atm Average speed of air molecules = 400 ms-1 Pressure - in terms of movement of particles • Air molecule bounces around inside, colliding with the various surfaces • Each collision exerts pressure on the box

If we have a box filled with gas: We can measure: n Pressure (Nm-2) n Temperature (K) n Volume (m 3) n Mass (kg)

Moles In the periodic table: 8 6 Oxygen = O 16 Carbon = C 12 Helium = He 24 Mass number = bottom number = molar mass • Mass number = mass (g) of 1 mole of that substance • 6. 02 x 1023 particles in 1 mole • e. g. 1 mole of He has a mass of 4 grams 1 mole of O 2 has a mass of 32 grams Mass (g) = number of moles x molar mass

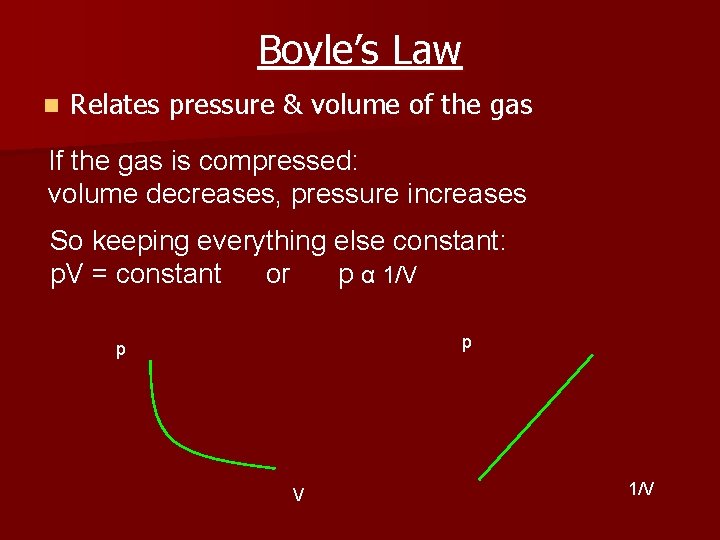
Boyle’s Law n Relates pressure & volume of the gas If the gas is compressed: volume decreases, pressure increases So keeping everything else constant: p. V = constant or p α 1/V p p V 1/V

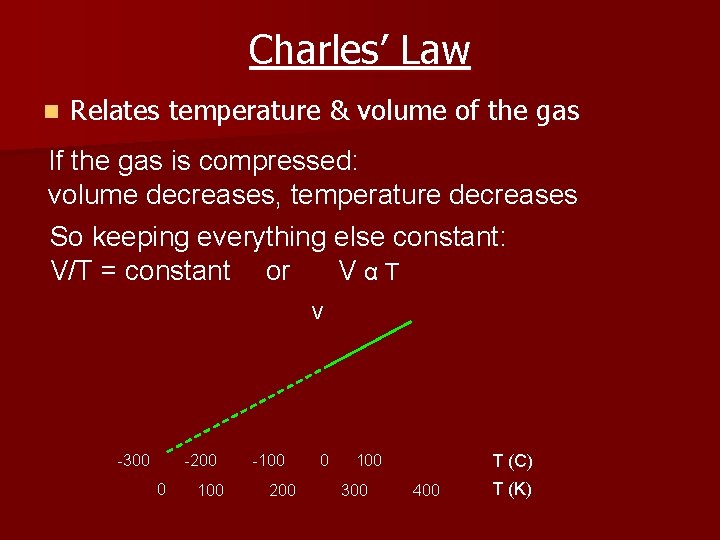
Charles’ Law n Relates temperature & volume of the gas If the gas is compressed: volume decreases, temperature decreases So keeping everything else constant: V/T = constant or VαT V -300 -200 0 100 -100 200 0 100 300 T (C) 400 T (K)

Pressure Law n Relates temperature & pressure of the gas If the gas is heated: temperature increases, pressure increases So keeping everything else constant: p/T = constant or pαT p 0 T (K)

Ideal Gas Equation The 3 gas laws can be written as a single equation which relates the 4 properties mentioned earlier p. V = n. RT where R = universal gas constant = 8. 31 Jmol-1 K-1 n, number of moles = mass (g) / molar mass (g mol-1) e. g. how many moles are there in 1. 6 kg of oxygen? molar mass of O 2 = 32 gmol-1 number of moles, n = 1600 g/32 gmol-1 = 50 mol

Summary n n n n n Vectors Projectiles Moments Power, Energy & Work Energy Changes Heat Capacity Newton’s 3 Laws Collisions Molecular Kinetic Theory
 Kinetic molecular theory of solids
Kinetic molecular theory of solids Kinetic theory for ideal gases
Kinetic theory for ideal gases Kinetic molecular theory volume
Kinetic molecular theory volume Kinetic molecular theory of liquids and solids
Kinetic molecular theory of liquids and solids Kinetic molecular theory of liquids
Kinetic molecular theory of liquids Kinetic energy molecular theory
Kinetic energy molecular theory Kinetic molecular theory def
Kinetic molecular theory def Theory vs hypothesis
Theory vs hypothesis Charles law in terms of kinetic molecular theory
Charles law in terms of kinetic molecular theory Postulates of kinetic molecular theory
Postulates of kinetic molecular theory Ideal gas law examples
Ideal gas law examples Postulates of kinetic theory of gases
Postulates of kinetic theory of gases Kinetic molecular theory formula
Kinetic molecular theory formula Kinetic molecular theory
Kinetic molecular theory Tenets of kinetic molecular theory
Tenets of kinetic molecular theory What is vbt
What is vbt Valence bond theory and molecular orbital theory
Valence bond theory and molecular orbital theory Valence bond theory and molecular orbital theory
Valence bond theory and molecular orbital theory Theories of covalent bonding
Theories of covalent bonding Hcn mo diagram
Hcn mo diagram Covalent bond melting point
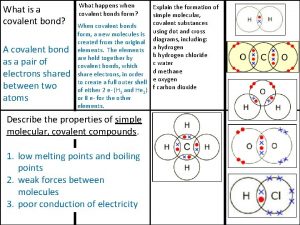
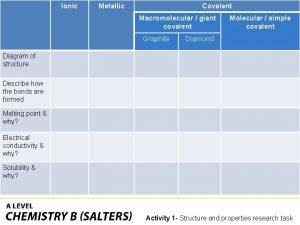
Covalent bond melting point Giant molecular structure vs simple molecular structure
Giant molecular structure vs simple molecular structure Zinc oxide + nitric acid → zinc nitrate + water
Zinc oxide + nitric acid → zinc nitrate + water The kinetic theory of matter states that
The kinetic theory of matter states that Kinetic theory of matter definition
Kinetic theory of matter definition Define kinetic theory of matter
Define kinetic theory of matter