Mechanics 105 Motion in one dimension chapter two

Mechanics 105 Motion in one dimension (chapter two) Motion diagrams, position-time graphs, etc. Average and instantaneous velocity Acceleration Particle under constant acceleration Freefall

Mechanics 105 Motion diagrams Motion diagram:

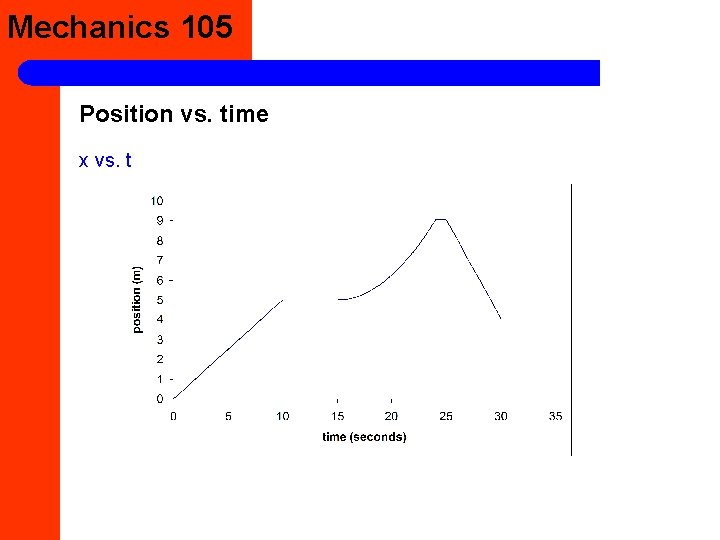
Mechanics 105 Position vs. time x vs. t

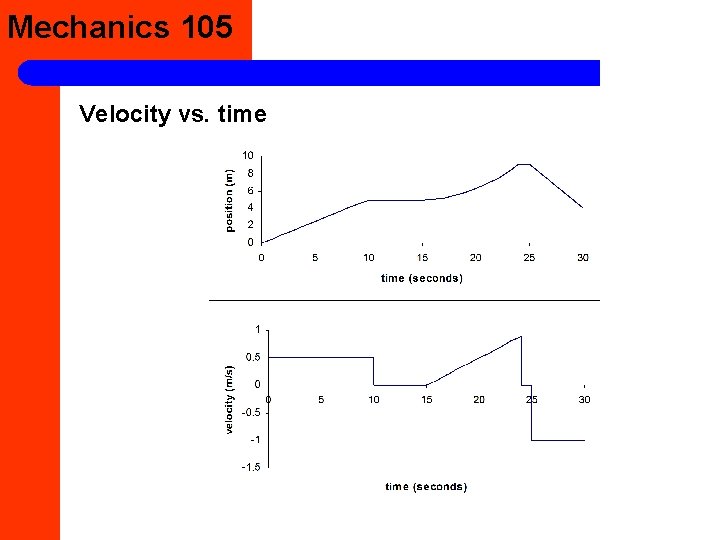
Mechanics 105 Velocity vs. time

Mechanics 105 Position vs. time Demo - ~constant velocity Conceptests http: //webphysics. davidson. edu/physletprob/ch 7_ in_class/in_class 7_1/mechanics 7_1_1. html http: //webphysics. davidson. edu/physletprob/ch 8_ problems/ch 8_1_kinematics/default. html

Mechanics 105 Average velocity l l l only depends on beginning and end points and time interval vector (scalar in 1 -d only) total displacement = integral of v(t)dt examples: A person runs 1 km in 5 minutes, then walks another 2 km in 20 minutes. What is their average velocity over the entire 3 km? Using the velocity vs. time graph shown earlier, find the average velocity and the total displacement l

Mechanics 105 Instantaneous velocity limit of average velocity as interval goes to zero l tangent to x(t) - derivative of x(t) vs. t l examples A ball rolling down a slope has a position described by the equation l What is the equation describing the instantaneous velocity? l Concep. Tests

Mechanics 105 Particle under constant velocity relation between initial and final displacement comes from the definition of average velocity average equals instantaneous

Mechanics 105 Acceleration average instantaneous

Mechanics 105 Particle moving under constant acceleration From definition of average acceleration: Displacement of particle = integral of velocity as a function of time

Mechanics 105 Particle moving under constant acceleration Combining previous two equations (removing a) Or (removing t)

Mechanics 105 Particle moving under constant acceleration Wide range of applications Zero acceleration: Free fall: acceleration due to gravity = 9. 80 m/s 2 downward (be careful about sign) If we define up to be the direction of the positive y axis, the equations of motion for a particle in free fall are: Note that the velocity can be positive or negative

Mechanics 105 Particle moving under constant acceleration Concep. Tests Demo – cart More physlets http: //webphysics. davidson. edu/physletprob/ch 8_problems/ch 8_1_kin ematics/default. html Examples

Mechanics 105 Example - braking distance (from Giancoli, 2 -10) Estimate minimum stopping distance for a car traveling at 60 mph 1) Maximum (negative) acceleration? 5~8 m/s 2 (dry road, good tires) 2) Typcial human response time? 0. 3 ~ 1. 0 sec (sober) part 1 – distance before brakes applied: part 2 – distance until car stops:

Mechanics 105 Example – Air bags (Giancoli 2 -11) If, instead of braking, the car in the previous example hit a tree, estiamte how fast the air bags need to inflate to do any good. estimate a stopping distance ~ 1. 00 m initial velocity = 26. 8 m/s final velocity = 0. 00 m/s first solve for a: then find t

Mechanics 105 Problem solving Choice of coordinate system can simplify problem Be consistent with signs (direction of chosen axis) Often problems involve two or more objects with some common variable (time, final displacement, etc. )