Mechanically Stabilized Earth Wall Structures MSE NZGS Auckland

Mechanically Stabilized Earth Wall Structures (MSE) NZGS Auckland Branch Mini Symposium 30 th November 2018

Mechanically Stabilized Earth Wall Structures (MSE) 1. Introduction MSE consists of three main components; 1. Facing elements 2. Compacted granular fill 3. Horizontal reinforcement Provides the compressive and shear strength Provide tensile strength for the MSE system

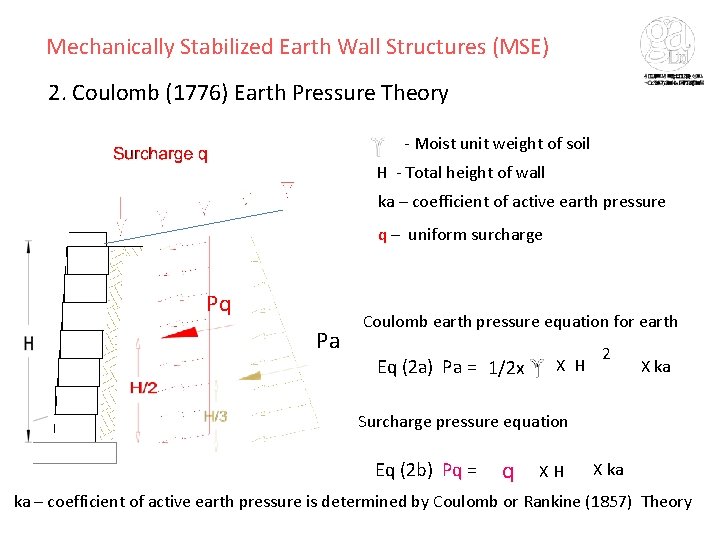
Mechanically Stabilized Earth Wall Structures (MSE) 2. Coulomb (1776) Earth Pressure Theory - Moist unit weight of soil H - Total height of wall ka – coefficient of active earth pressure q – uniform surcharge Pq Pa Coulomb earth pressure equation for earth Eq (2 a) Pa = 1/2 x X H 2 X ka Surcharge pressure equation Eq (2 b) Pq = q XH X ka ka – coefficient of active earth pressure is determined by Coulomb or Rankine (1857) Theory

Mechanically Stabilized Earth Wall Structures (MSE) 3. Determination of ka – coefficient of active earth = angle of internal friction of soil = slope angle above wall = angle of batter of wall from horizontal = batter of wall measured from vertical = angle of friction at back of wall By Rankine By Coulomb Pa = angle of failure plane from the horizontal R Pa = 90 deg Force diagram R Force diagram

Mechanically Stabilized Earth Wall Structures (MSE) 4. Bearing Capacity at base the of MSE 4. 1. 1 Determination by Meyerhof 4. 1. 2 Ultimate Bearing Capacity of soil can be calculated from Meyerhof equation ( Qult ) e Qult e Eq 4. 4 Factor of Safety for bearing= B = Total length of base Mr = sum of resisting moments Mo = sum of overturning moments Mr = q X L + WXL Mo = q X H/2 + Pah x H/3 = calculated applied bearing pressure Limit of eccentricity Qult e >2. 5 < B/6

Mechanically Stabilized Earth Wall Structures (MSE) 5. External Stability Analysis Active Earth Pressure for static 5. 1. External sliding 5. 2 Overturning Live load surcharge is included as Resisting force for the determination of eccentricity and bearing pressure However live load surcharge q is not included as a resisting force in the external sliding and overtuning analysis

Mechanically Stabilized Earth Wall Structures (MSE) 6. External Stability Analysis for seismic (dynamic) Seismic Parameters A = Peak Ground Acceleration Am = Peak Structural acceleration for A < 0. 45, Am = A(1. 45 – A) for A > 0. 45, Am = A kh (ext) = Ext. Hori. Seismic coefficient , for min displacement kh (ext) = Am for “ 10 A” inch displacement kh (ext) = Am/2 kh (int) = Am, Internal horizontal Seismic coefficient kv = Vertical Seismic coefficient, usually assumed zore Surcharge varies from zero to 50% Total earth thrust = dynamic + static based on Mononobe-Okabe (Kae) Inertia Dynamic Forces Total surcharge thrust = dynamic + static Seismic thrust (dynamic) on external

Mechanically Stabilized Earth Wall Structures (MSE) 7. Internal Stability Analysis Failu re p la ne - Rank i ne 7. 1 The tensile elements do not exceed working stress 7. 2 The tensile elements have adequate connection capacity to facing elements 7. 3 The tensile elements have adequate anchorage beyond the potential failure plane to hold the wedge of the soil in place 7. 4 There is no potential surface where the mass can shear internally 7. 5 There is stability of facing elements against shear, bulging and overturning Earth pressure resisted by top reinforcement Earth pressure resisted by second reinforcement Earth pressure resisted by third reinforcement Earth pressure resisted by forth reinforcement Earth pressure resisted by fifth reinforcement Internal Stress Distribution

Mechanically Stabilized Earth Wall Structures (MSE) 8. Internal Stability Analysis 8. 1 Tension Level Calculation For inextensible reinforcement the lateral earth pressure coefficient varies with depth from ko to ka for Coherent Gravity Method. kr ka ka kr Tn Tn Tributary area kr ka Whereas for the Simplified Method the lateral earth pressure coefficient kr varies with depth as well as the type of inextensible reinforcement Tension in each layer of reinforcement Tn ka q* ka extensible ka = coefficient of active earth pressure (Coulomb or Rankine) For extensible reinforcement - Geosynthetic reinforcement Tn kr q*kr Inextensible For Simplified Method

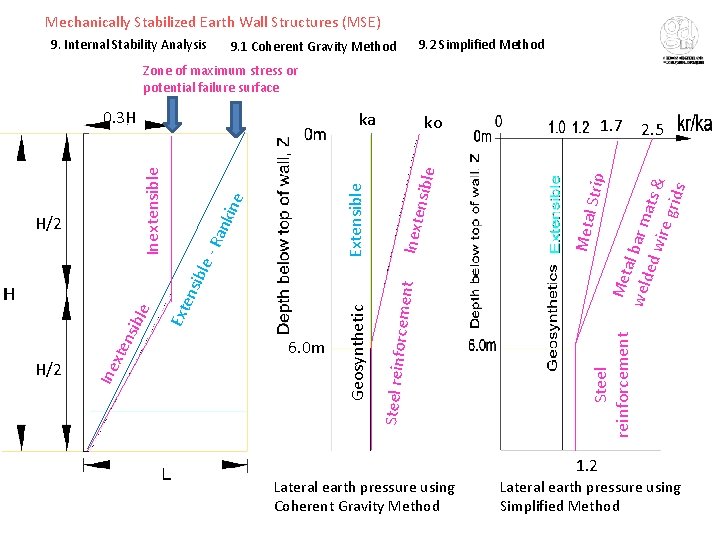
Mechanically Stabilized Earth Wall Structures (MSE) 9. Internal Stability Analysis 9. 2 Simplified Method 9. 1 Coherent Gravity Method Zone of maximum stress or potential failure surface 2. 5 Met a weld l bar m ed w ats & ire g rids Strip 1. 7 Steel reinforcement Inexte nsible ko Steel reinfo Extensible nki - Ra ens Ext 6. 0 m Geosynthetic Ine H/2 xte nsi ble ible H/2 ne Inextensible ka Metal 0. 3 H 1. 2 Lateral earth pressure using Coherent Gravity Method Lateral earth pressure using Simplified Method

Mechanically Stabilized Earth Wall Structures (MSE) 10. Internal Stability Analysis 10. 1. Strip loads 10. 2 Abutment – Simply supported Active Zone reinforcement Failure surface Potential Failure surface for inextensible reinforcement Pv reinforcement Tn Tributary area reinforcement Resistant Zone Distribution of vertical stress 2 V to 1 H profile with depth Strip loads Internal Design for inextensible reinforcement of MSE kr q *kr Tn + Kr *

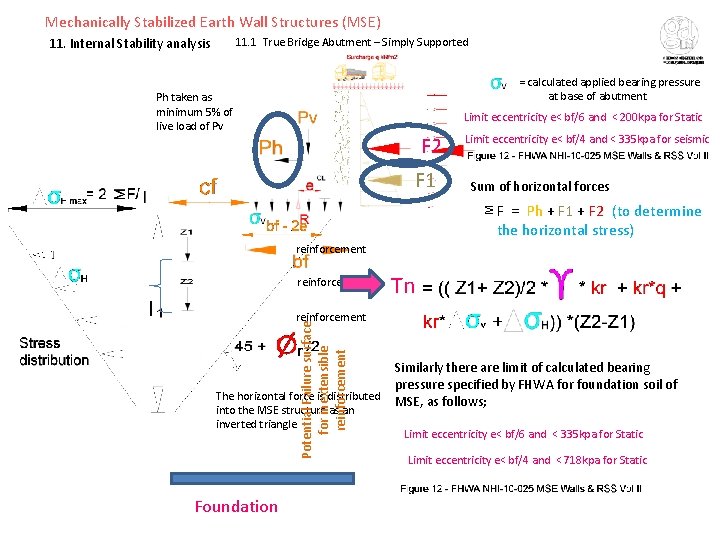
Mechanically Stabilized Earth Wall Structures (MSE) 11. Internal Stability analysis 11. 1 True Bridge Abutment – Simply Supported = calculated applied bearing pressure at base of abutment Ph taken as minimum 5% of live load of Pv Limit eccentricity e< bf/6 and < 200 kpa for Static F 2 Sum of horizontal forces M F 1 Limit eccentricity e< bf/4 and < 335 kpa for seismic F = Ph + F 1 + F 2 (to determine the horizontal stress) reinforcement Tn Potential Failure surface for inextensible reinforcement The horizontal force is distributed into the MSE structure as an inverted triangle Foundation Similarly there are limit of calculated bearing pressure specified by FHWA for foundation soil of MSE, as follows; Limit eccentricity e< bf/6 and < 335 kpa for Static Limit eccentricity e< bf/4 and < 718 kpa for Static

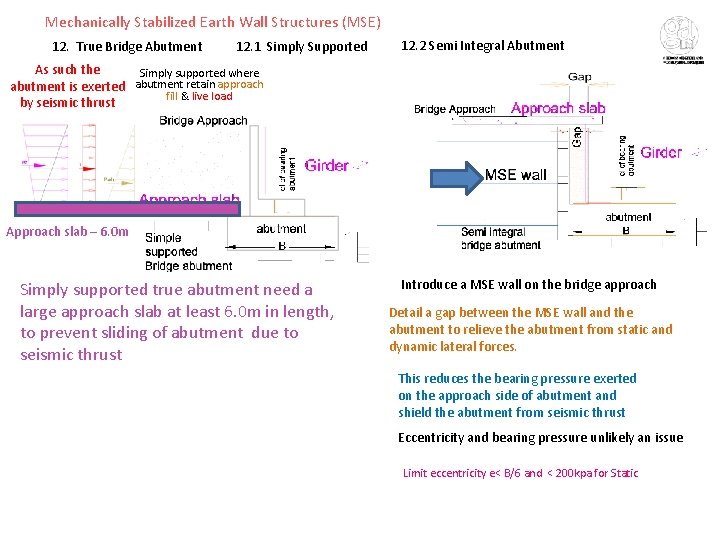
Mechanically Stabilized Earth Wall Structures (MSE) 12. True Bridge Abutment 12. 1 Simply Supported 12. 2 Semi Integral Abutment As such the Simply supported where abutment is exerted abutment retain approach fill & live load by seismic thrust Approach slab – 6. 0 m Simply supported true abutment need a large approach slab at least 6. 0 m in length, to prevent sliding of abutment due to seismic thrust Introduce a MSE wall on the bridge approach Detail a gap between the MSE wall and the abutment to relieve the abutment from static and dynamic lateral forces. This reduces the bearing pressure exerted on the approach side of abutment and shield the abutment from seismic thrust Eccentricity and bearing pressure unlikely an issue Limit eccentricity e< B/6 and < 200 kpa for Static

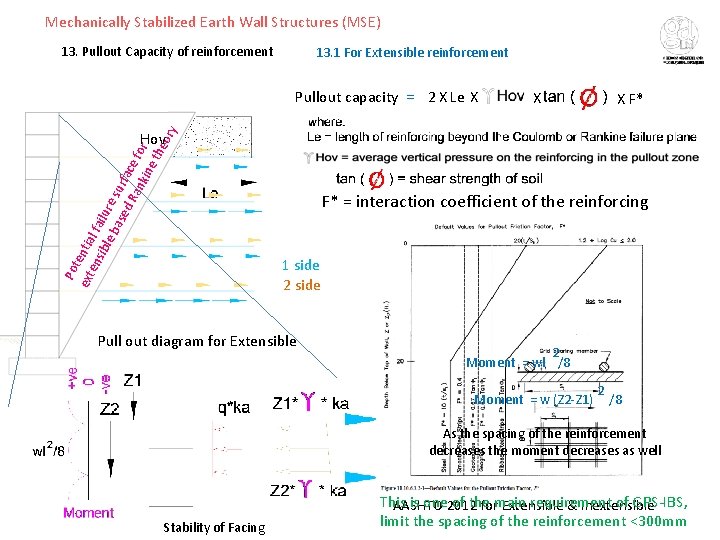
Mechanically Stabilized Earth Wall Structures (MSE) 13. Pullout Capacity of reinforcement 13. 1 For Extensible reinforcement Po t ext entia en sib l failu le b re ase surf d R ace ank fo ine r the ory Pullout capacity = 2 X Le X X X F* Hov F* = interaction coefficient of the reinforcing 1 side 2 side Pull out diagram for Extensible 2 Moment = wl /8 Moment = w (Z 2 -Z 1) 2 /8 As the spacing of the reinforcement decreases the moment decreases as well Stability of Facing This is one 2012 of the requirement of GRS-IBS, AASHTO formain Extensible & Inextensible limit the spacing of the reinforcement <300 mm

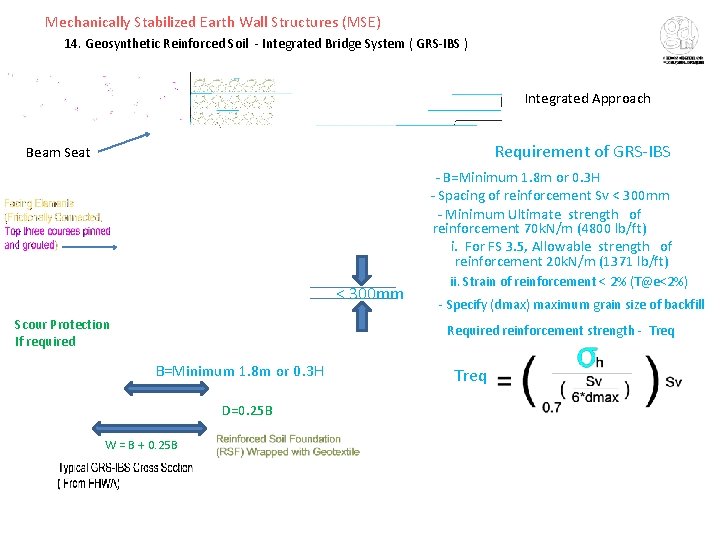
Mechanically Stabilized Earth Wall Structures (MSE) 14. Geosynthetic Reinforced Soil - Integrated Bridge System ( GRS-IBS ) Integrated Approach Requirement of GRS-IBS Beam Seat - B=Minimum 1. 8 m or 0. 3 H - Spacing of reinforcement Sv < 300 mm - Minimum Ultimate strength of reinforcement 70 k. N/m (4800 lb/ft) i. For FS 3. 5, Allowable strength of reinforcement 20 k. N/m (1371 lb/ft) < 300 mm Scour Protection If required ii. Strain of reinforcement < 2% (T@e<2%) - Specify (dmax) maximum grain size of backfill Required reinforcement strength - Treq B=Minimum 1. 8 m or 0. 3 H D=0. 25 B W = B + 0. 25 B Treq

Mechanically Stabilized Earth Wall Structures (MSE) 15. Conclusion 1. The salient feature of MSE structures is the ability to accommodate settlement 2. Though the AASHTO code has specified an allowable of 1% maximum differential settlement, MSE tolerates much higher differential magnitude. As such, MSE structures are excellence option for retaining function. 3. The application of MSE to directly support the bridge, true bridge abutment, the strict adherence of the maximum allowable of 1% differential settlement is desirable to ensure that the serviceability requirement is not compromise. 4. Since a high percentage of total settlement is due to the self-weight of MSE, this phenomena is commonly exploited in the true bridge abutment structures as elevation losses can be compensated prior the construction of the abutment. 6. The emergence of high strength low extensible geosynthetic has allowed accelerated bridge construction, Geosynthetic Reinforced Soil - Integrated Bridge System ( GRS-IBS) to be realised. 7. As MSE structures are economical, simple and environmentally friendly in construction, these structures provide a good solution for retaining as well as load supporting options when site conditions suit their application.

Mechanically Stabilized Earth Wall Structures (MSE) Acknowledgement and References Questions?