Mechanical Unit Operations Chapter 1 PROPERTIES OF PARTICULATE

Mechanical Unit Operations Chapter (1) PROPERTIES OF PARTICULATE SOLIDS • The main properties that characterize solid particles are: • Density • Shape • Size of these particles.

1. 4. Particle Size The “Equivalent diameter” of a particle is the main dimension if the particle is equi-dimensional (Diameter in a sphere, Edge length in a cube etc…). For irregular particles, it is usually taken as the 2 nd largest dimension. Particles are termed coarse if their diameters are in the range of a few centimeters or millimeters, they are considered fine when their diameters are in the range of tens or hundreds of microns and very fine if the particle size is in the range of a few microns or less. A crushed product will usually consist of coarse to fine particles while a ground product will consist only of fine particles.

1. 4. Particle Size 1. 4. 1 Standard screen series (or standard sieves) Standard screens are used to measure the size and size distribution of particles in the size range 80 mm to 40 µm. They are made of woven wire screens, the mesh and dimensions of which are carefully standardized. The openings are square. Each screen is identified by the “mesh size” which represents the number of openings per linear inch. The actual openings are smaller than the mesh size because of the thickness of the wires.

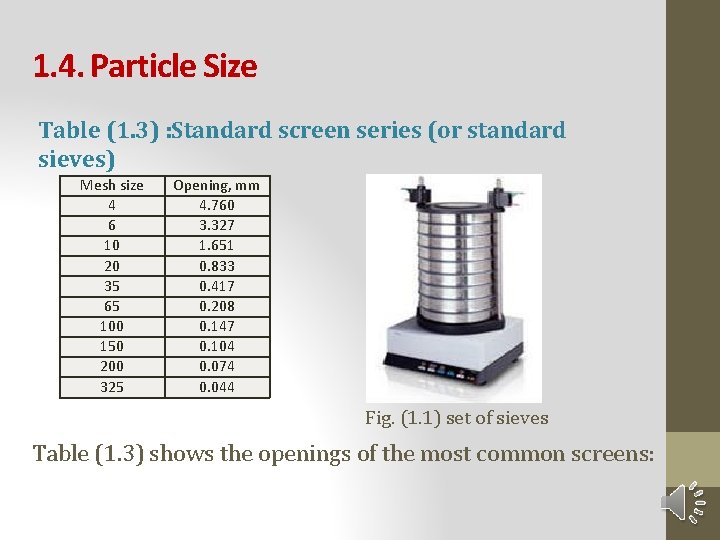
1. 4. Particle Size Table (1. 3) : Standard screen series (or standard sieves) Mesh size 4 6 10 20 35 65 100 150 200 325 Opening, mm 4. 760 3. 327 1. 651 0. 833 0. 417 0. 208 0. 147 0. 104 0. 074 0. 044 Fig. (1. 1) set of sieves Table (1. 3) shows the openings of the most common screens:

1. 4. Particle Size 1. 4. 1 Screen analysis To sort a sample of particles of different sizes, one uses a set of screens arranged vertically in a decreasing order of opening diameter from top to bottom. The upper screen is usually chosen in such a way that no particles will be left on its surface on screening the mixture. Also the bottom screen is chosen such that a minimum amount of fine powder will drop in the pan placed beneath the set of screens. (Fig. 1. 1)

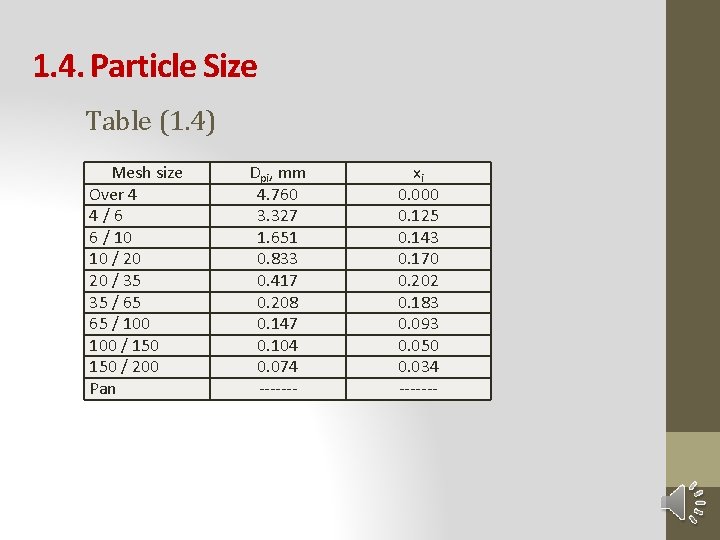
1. 4. Particle Size The mass of particles retained over the screen No. (i), numbered from top, is mi. The total mass is M = m 1 + m 2 + …. + mn The mass fraction of particles retained over this screen is: xi = mi/M (1. 5) • The symbol Dpi will denote the particle diameter corresponding to the opening of the screen No. (i). A table showing the values of xi against those of Dpi is termed “A Differential analysis”. An example of such analysis is shown in Table (1. 4)

1. 4. Particle Size Table (1. 4) Mesh size Over 4 4/6 6 / 10 10 / 20 20 / 35 35 / 65 65 / 100 / 150 / 200 Pan Dpi, mm 4. 760 3. 327 1. 651 0. 833 0. 417 0. 208 0. 147 0. 104 0. 074 ------- xi 0. 000 0. 125 0. 143 0. 170 0. 202 0. 183 0. 093 0. 050 0. 034 -------

1. 4. Particle Size 0. 25 xi 0. 2 0. 15 0. 1 0. 05 0 0 0. 5 1 1. 5 2 2. 5 3 3. 5 Fig. (1. 2) Differential analysis 4 4. 5 Dp mm 5

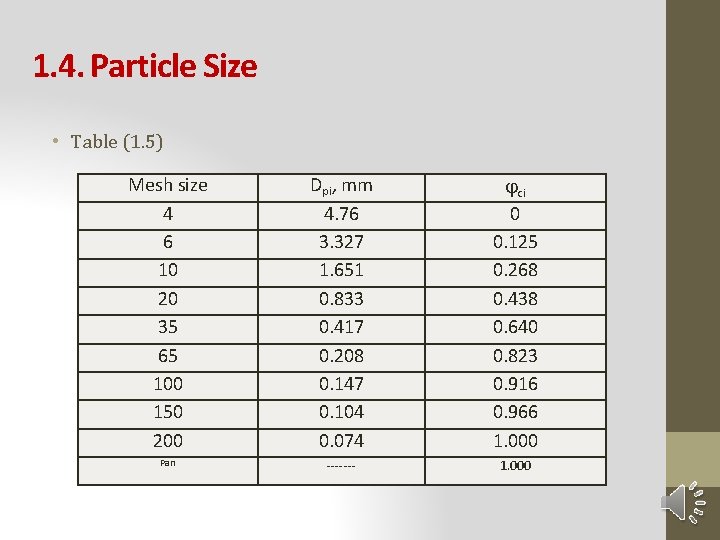
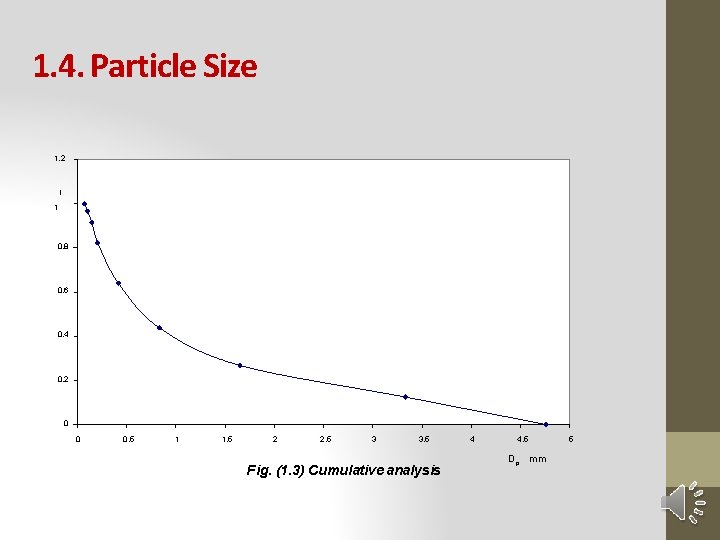
1. 4. Particle Size • Another analysis of interest is the “Cumulative Analysis” showing the cumulative fraction that would rest over a certain screen if all the screens above this screen were removed. • It then gives the fraction of particles that would be retained on any screen (φci). Table (1. 5) shows the cumulative analysis corresponding to the data of Table (1. 4)

1. 4. Particle Size • Table (1. 5) Mesh size 4 6 10 20 35 65 100 150 200 Dpi, mm 4. 76 3. 327 1. 651 0. 833 0. 417 0. 208 0. 147 0. 104 0. 074 ci 0 0. 125 0. 268 0. 438 0. 640 0. 823 0. 916 0. 966 1. 000 Pan ------- 1. 000

1. 4. Particle Size 1. 2 i 1 0. 8 0. 6 0. 4 0. 2 0 0 0. 5 1 1. 5 2 2. 5 3 3. 5 Fig. (1. 3) Cumulative analysis 4 4. 5 Dp mm 5

1. 4. Particle Size 1. 4. 3 Specific surface of a mixture ( Aw ) This is defined as the total surface area of the particles per unit mass and can be obtained for spherical particles of equal diameter Dp by: If the particles are of irregular shape , then: (1. 7) If now the differential screen analysis of the mixture is known, then the total surface area of the particles resting over the ith screen is:

1. 4. Particle Size Where Davi is the average diameter between the (i-1)th and the ith screens. The specific surface area is therefore: (1. 8) If the cumulative analysis is used, the corresponding formula is: (1. 9) This requires plotting (1/Dp) vs. φc and performing graphical integration.

Thank You