Mechanical Mode Damping for Parametric Instability Control Matt

Mechanical Mode Damping for Parametric Instability Control Matt Evans Jonathan Soto Gaviard Dennis Coyne Peter Fritschel

Motivation for focusing on mechanical mode Qs q Recall: parametric gain is proportional to mechanical 10 -100 million mode Qm: q Past work looked at ‘broadband’ dampers on the test mass barrel (Zhao et al. , UWA) Ø Uniform barrel coating; localized damping ring around barrel Ø Not very satisfying effectiveness: thermal noise increased by 10% (100 Hz), but mode Qs still several million q Want a more frequency selective approach Ø Active damping using the test mass actuators (electro-static drive) Ø Passive damping using added tuned mass dampers 2

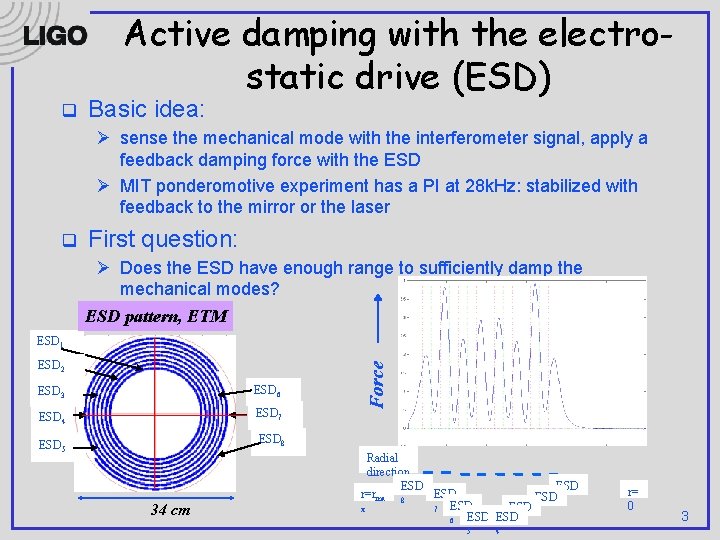
Active damping with the electrostatic drive (ESD) q Basic idea: Ø sense the mechanical mode with the interferometer signal, apply a feedback damping force with the ESD Ø MIT ponderomotive experiment has a PI at 28 k. Hz: stabilized with feedback to the mirror or the laser q First question: Ø Does the ESD have enough range to sufficiently damp the mechanical modes? ESD pattern, ETM ESD 2 ESD 3 ESD 6 ESD 4 ESD 7 ESD 5 ESD 8 34 cm Force ESD 1 Radial direction ESD r=rma 8 ESD 1 ESD 2 x 7 ESD 6 3 5 4 r= 0 3

ESD mode damping q Required force: mode freq. overlap w/ ESD q modal mass rms modal amplitude thermal excitation: damped Q Available ESD force Ø 200 micro-Newton peak, acquisition mode Ø Few micro-Newtons in low-noise mode 4

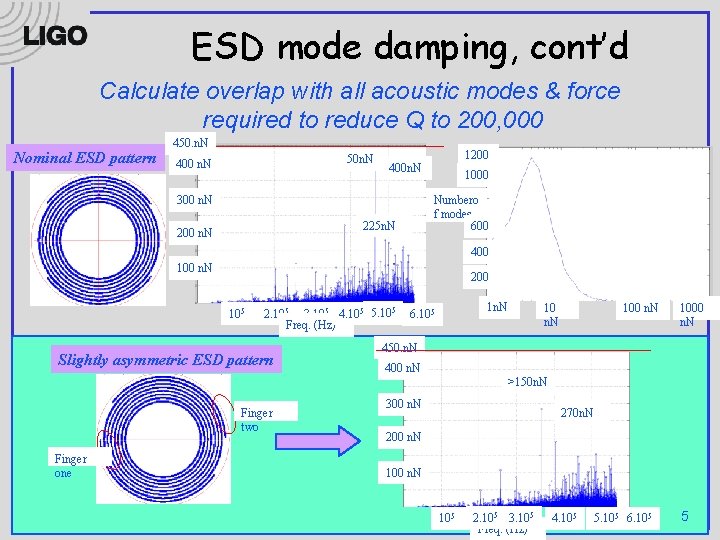
ESD mode damping, cont’d Calculate overlap with all acoustic modes & force required to reduce Q to 200, 000 Nominal ESD pattern 450. n. N 50 n. N 400 n. N 1000 Numbero f modes 600 300 n. N 225 n. N 200 n. N 1200 400 100 n. N 200 105 2. 105 3. 105 4. 105 5. 105 Freq. (Hz) Slightly asymmetric ESD pattern 1 n. N 6. 105 10 n. N 1000 n. N 450. n. N 400 n. N >150 n. N Finger two Finger one 300 n. N 270 n. N 200 n. N 105 2. 105 3. 105 Freq. (Hz) 4. 105 5. 105 6. 105 5

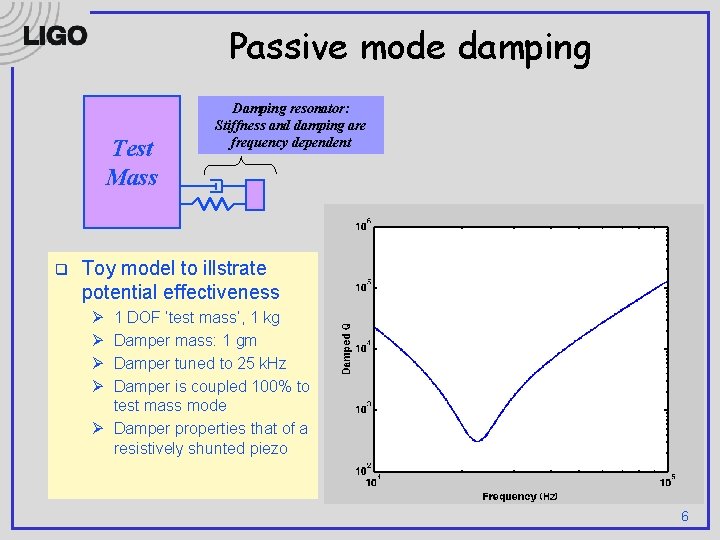
Passive mode damping Test Mass q Damping resonator: Stiffness and damping are frequency dependent Toy model to illstrate potential effectiveness Ø Ø 1 DOF ‘test mass’, 1 kg Damper mass: 1 gm Damper tuned to 25 k. Hz Damper is coupled 100% to test mass mode Ø Damper properties that of a resistively shunted piezo 6

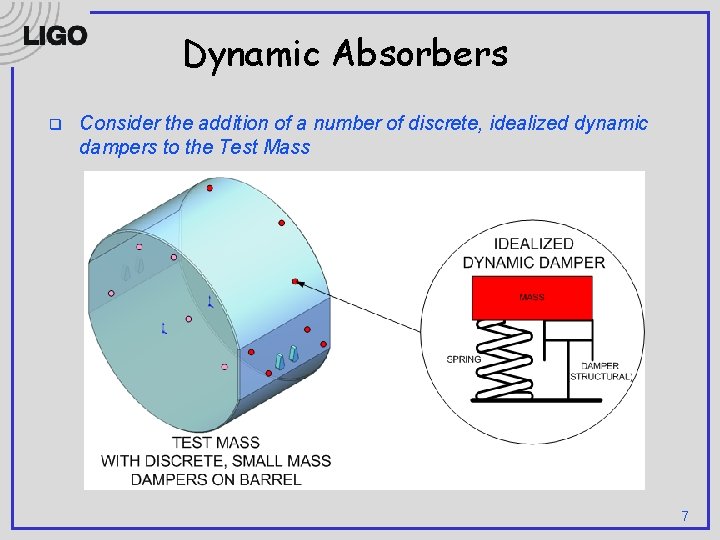
Dynamic Absorbers q Consider the addition of a number of discrete, idealized dynamic dampers to the Test Mass 7

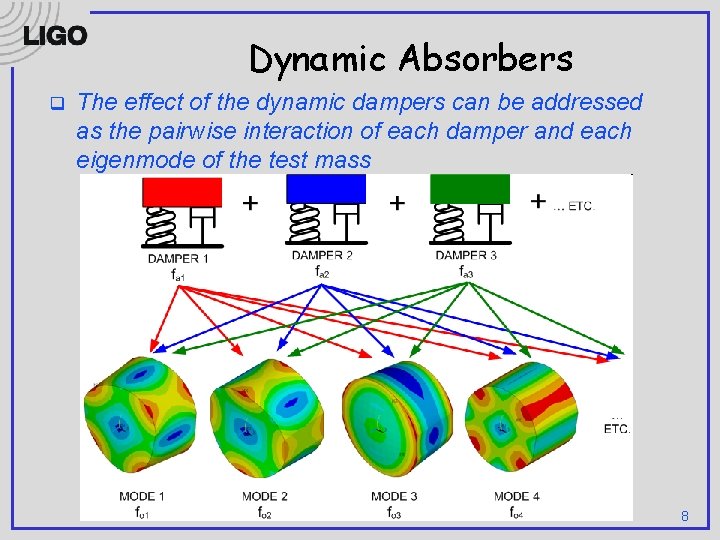
Dynamic Absorbers q The effect of the dynamic dampers can be addressed as the pairwise interaction of each damper and each eigenmode of the test mass 8

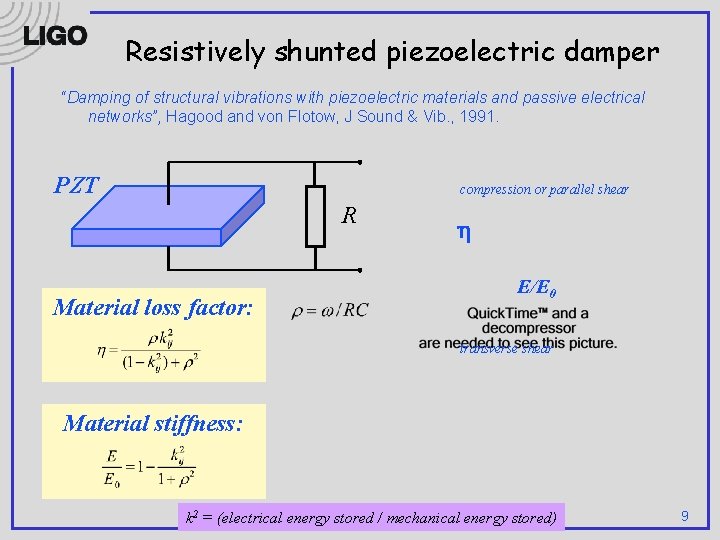
Resistively shunted piezoelectric damper “Damping of structural vibrations with piezoelectric materials and passive electrical networks”, Hagood and von Flotow, J Sound & Vib. , 1991. PZT compression or parallel shear R Material loss factor: E/E 0 transverse shear Material stiffness: k 2 = (electrical energy stored / mechanical energy stored) 9

Selection of acoustical modes q q Determine which acoustical modes might be problematic, so we don’t always have to look at all ~10, 000 modes between 10 -100 k. Hz Calculate parametric gain R for a single arm cavity: Ø Include Hermite-Gauss modes up to order m+n=8 Ø Approximate optical mode diffraction loss as 2 x clipping loss Ø Artificially widen the cavity optical modes (but don’t lower their Q) to account for uncertainty in mirror radii of curvature (used d. R = +/- 10 m) Ø Take acoustic mode Q = 10 million Ø Accept all modes with R greater than 0. 1 Ø End up with 675 modes between 10 -90 k. Hz v Caveat: higher frequencies need to be redone with higher resolution FEA 10

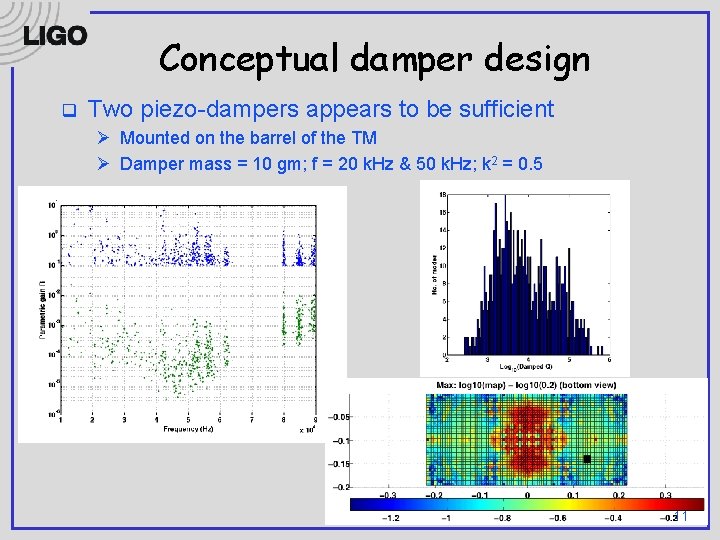
Conceptual damper design q Two piezo-dampers appears to be sufficient Ø Mounted on the barrel of the TM Ø Damper mass = 10 gm; f = 20 k. Hz & 50 k. Hz; k 2 = 0. 5 11

Piezo damper details q Thermal noise impact Ø Combination of resonant design, loss function of the piezo, and the physical location, leads to negligible thermal noise impact due to piezo damping Ø More important with be TM surface strain energy coupling to damper materials and bonds: this needs to be estimated q Practical design: it’s essentially a piezo-electric accelerometer Ø Tri-axial sensitivity may be important Ø Need a rigid, vacuum-compatible structure 12

Plans q Initial LIGO test mass and suspension test Ø Try damping a couple of ~10 k. Hz modes from a Q of a million to a ~100, 000, using a piezo-damper (with a commercial accelerometer) q LASTI test mass, suspended in the quad suspension with glass fibers (to be installed) Ø Measure internal mode Qs Ø Try damping Qs using the electro-static drive Ø Piezo-damper ? ? 13