Meccanica Cinematica del punto materiale Velocit accelerazione moto

Meccanica • Cinematica del punto materiale Velocità, accelerazione, moto rettilineo uniforme, moto uniformemente accelerato, moto circolare uniforme • Dinamica Forza, principi della dinamica, descrizione di diversi tipi di forza, attrito, quantità di moto, momento di una forza • Energia e leggi di conservazione Lavoro di una forza, energia cinetica e potenziale, conservazione dell’energia, rendimento • Statica dei corpi rigidi Condizioni di equilibrio di un corpo rigido, leve

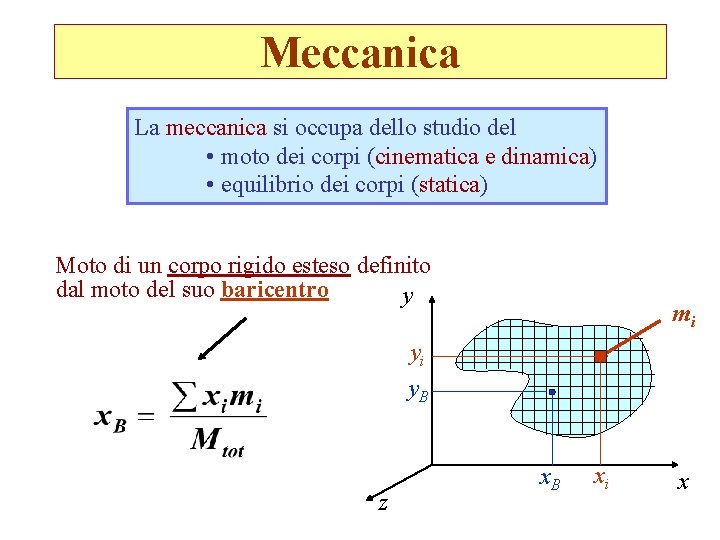
Meccanica La meccanica si occupa dello studio del • moto dei corpi (cinematica e dinamica) • equilibrio dei corpi (statica) Moto di un corpo rigido esteso definito dal moto del suo baricentro y mi yi y. B z x. B xi x

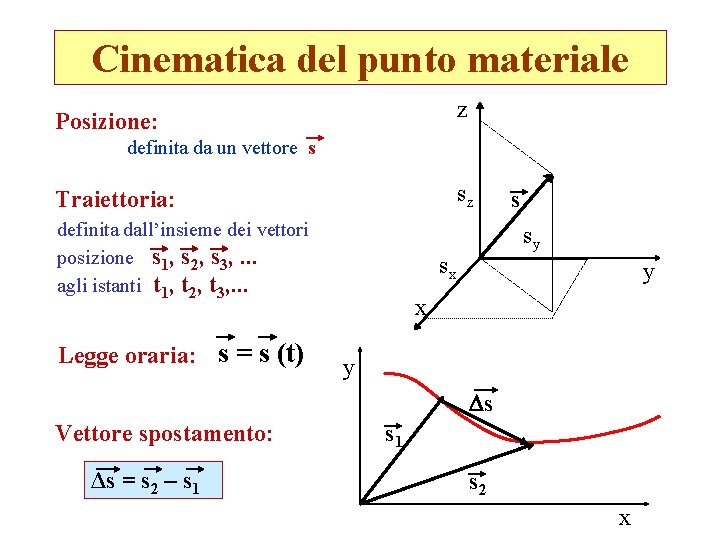
Cinematica del punto materiale z Posizione: definita da un vettore s sz Traiettoria: definita dall’insieme dei vettori posizione s 1, s 2, s 3, . . . agli istanti t 1, t 2, t 3, . . . Legge oraria: s = s (t) s sy sx y s Vettore spostamento: Δs = s 2 – s 1 s 2 x

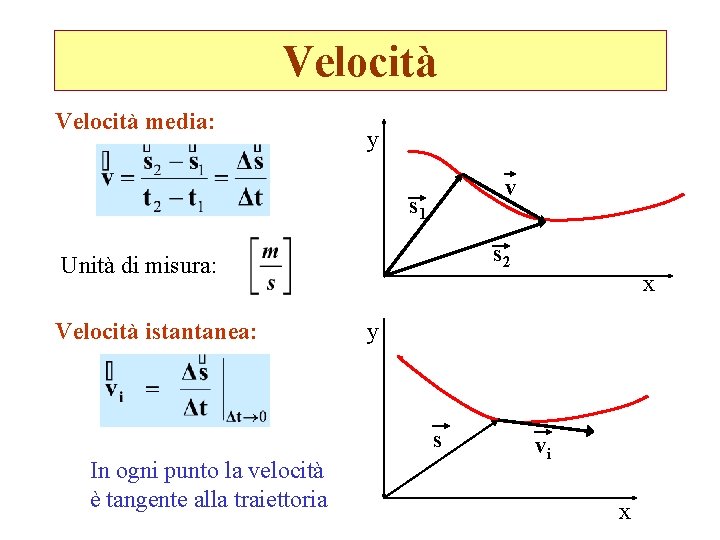
Velocità media: y v s 1 s 2 Unità di misura: Velocità istantanea: y s In ogni punto la velocità è tangente alla traiettoria x vi x

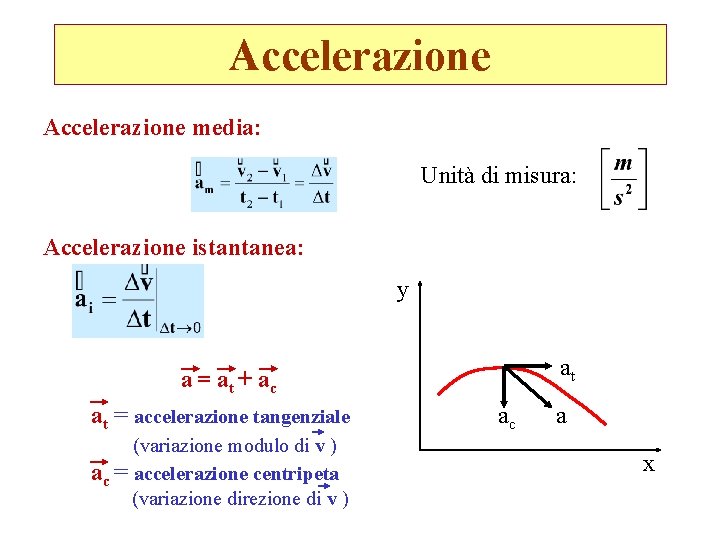
Accelerazione media: Unità di misura: Accelerazione istantanea: y at a = at + ac at = accelerazione tangenziale (variazione modulo di v ) ac = accelerazione centripeta (variazione direzione di v ) ac a x

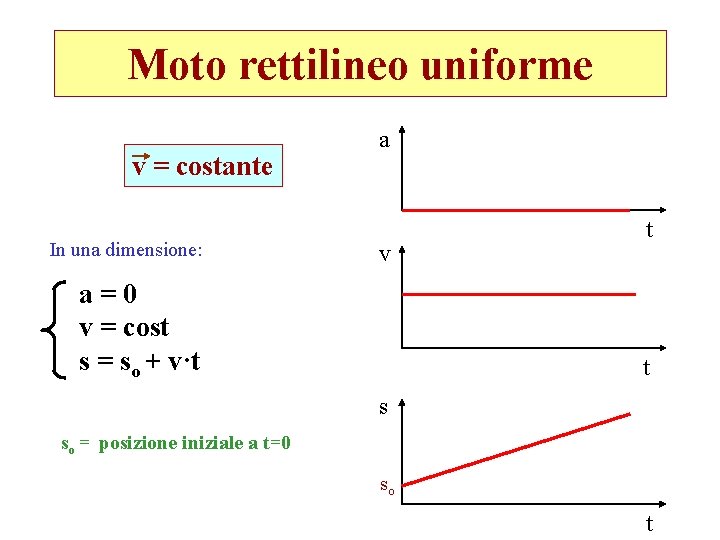
Moto rettilineo uniforme v = costante In una dimensione: a v a=0 v = cost s = so + v·t t t s so = posizione iniziale a t=0 so t

Moto rettilineo uniforme Esempio: Spazio percorso dopo Δt=10 s ? a=0 v = cost s = s 0 + v·t

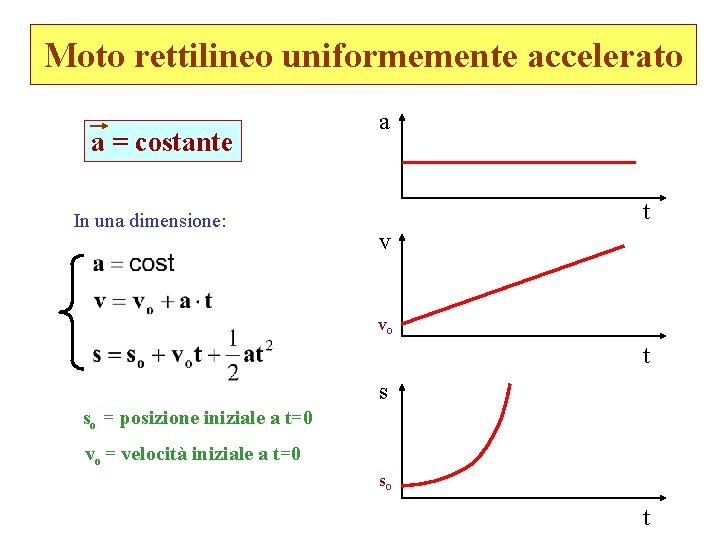
Moto rettilineo uniformemente accelerato a = costante In una dimensione: a t v vo t s so = posizione iniziale a t=0 vo = velocità iniziale a t=0 so t

Moto rettilineo uniformemente accelerato caduta di un grave in assenza di attrito Accelerazione di gravità Vo = 0 h Esempio: h = 10 m

Moto circolare uniforme Velocità angolare v v Velocità lineare ac [s-1 = Hz] Frequenza r [s] Periodo no accelerazione tangenziale at=0 v cambia in direzione acc. centripeta : v

Moto circolare uniforme Esempio: Centrifuga di raggio R = 20 cm, che ruota a 3000 giri/minuto a) frequenza: b) periodo: Tempo per compiere 1 giro completo c) velocità angolare: d) velocità lineare o periferica: Velocità di un punto sul bordo della centrifuga

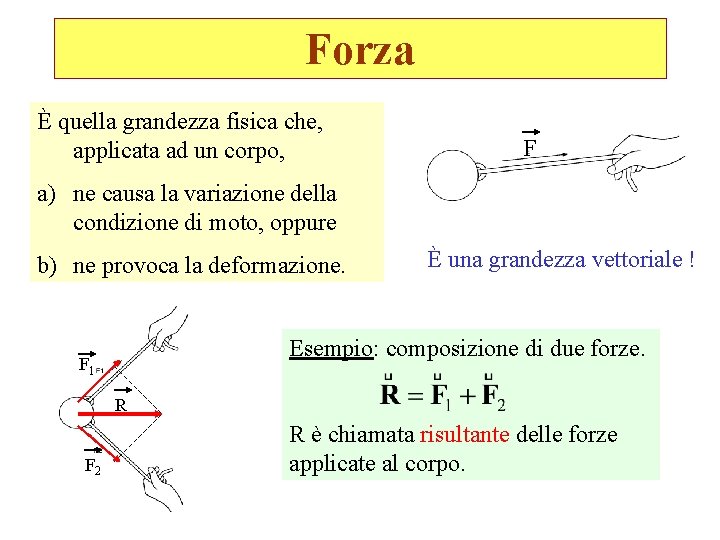
Forza È quella grandezza fisica che, applicata ad un corpo, F a) ne causa la variazione della condizione di moto, oppure b) ne provoca la deformazione. È una grandezza vettoriale ! Esempio: composizione di due forze. F 1 R F 2 R è chiamata risultante delle forze applicate al corpo.

Principi della dinamica 1. Principio di inerzia: un corpo non soggetto a forze permane nel suo stato di quiete o di moto rettilineo uniforme 2. Legge di Newton: Unità di misura (S. I. ): 3. Principio di azione e reazione: ad ogni azione corrisponde una reazione uguale e contraria

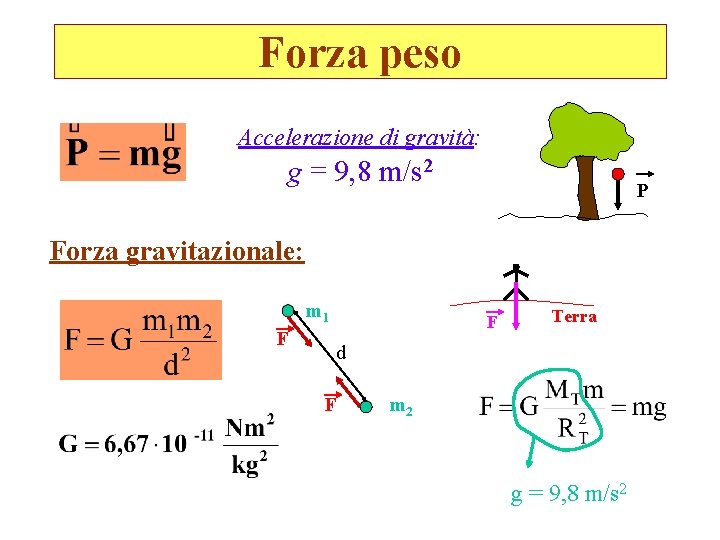
Forza peso Accelerazione di gravità: g = 9, 8 m/s 2 P Forza gravitazionale: m 1 F F Terra d F m 2 g = 9, 8 m/s 2

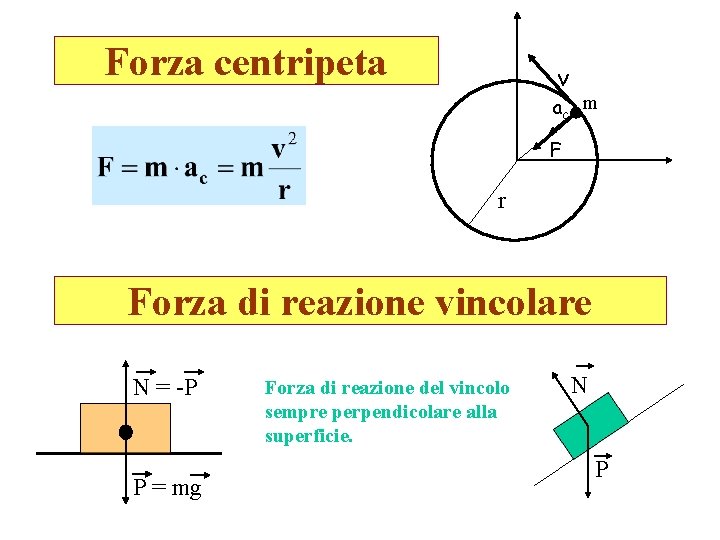
Forza centripeta v ac m F r Forza di reazione vincolare N = -P P = mg Forza di reazione del vincolo sempre perpendicolare alla superficie. N P

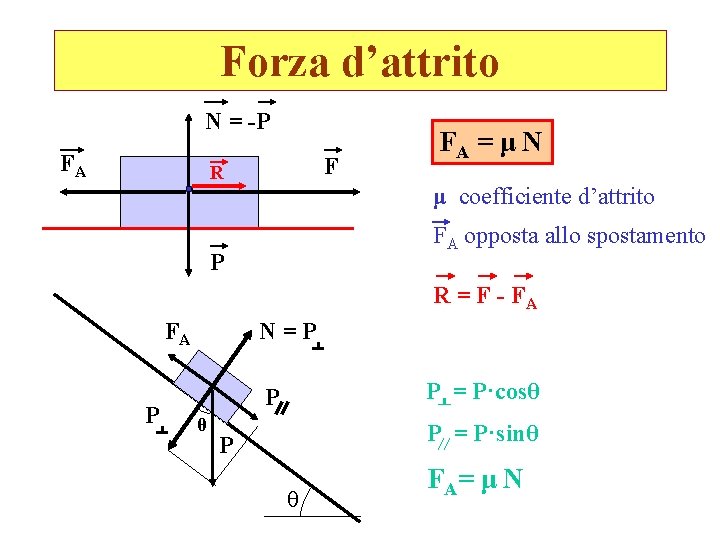
Forza d’attrito N = -P FA F R FA = μ N μ coefficiente d’attrito FA opposta allo spostamento P R = F - FA FA P N=P P = P·cosθ P = P·sinθ P θ F A= μ N

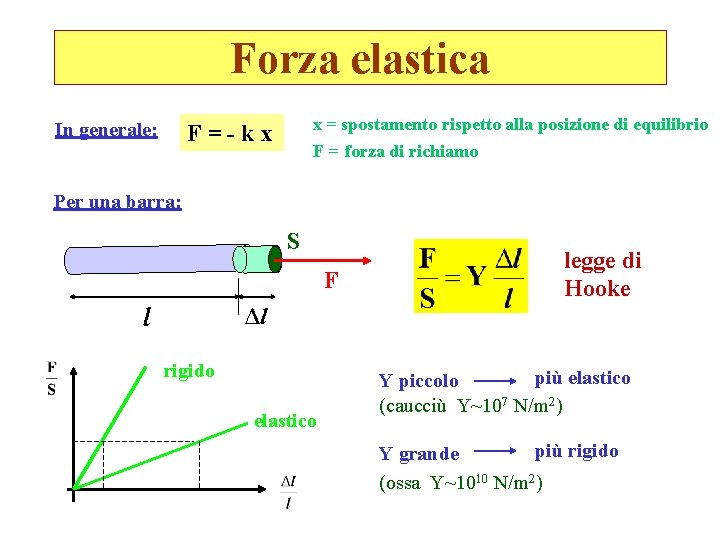
Forza elastica In generale: x = spostamento rispetto alla posizione di equilibrio F=-kx F = forza di richiamo Per una barra: S F l legge di Hooke Δl rigido elastico più elastico Y piccolo (caucciù Y~107 N/m 2) più rigido Y grande (ossa Y~1010 N/m 2)

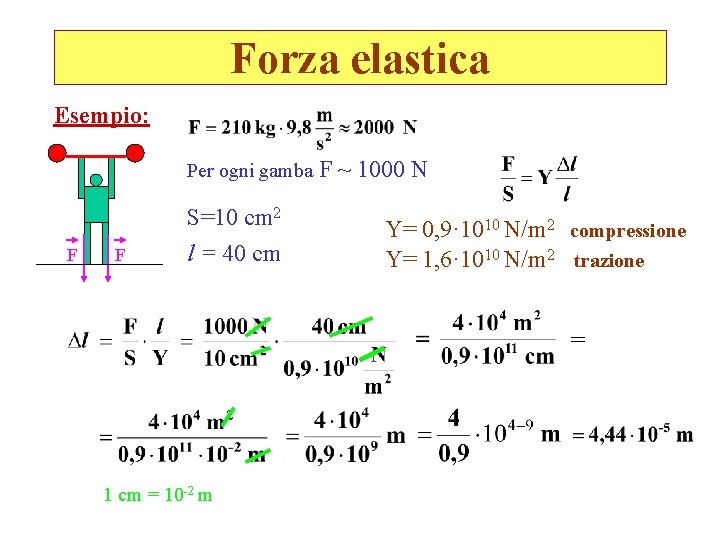
Forza elastica Esempio: Per ogni gamba F F S=10 cm 2 l = 40 cm F ~ 1000 N Y= 0, 9· 1010 N/m 2 compressione Y= 1, 6· 1010 N/m 2 trazione = 1 cm = 10 -2 m

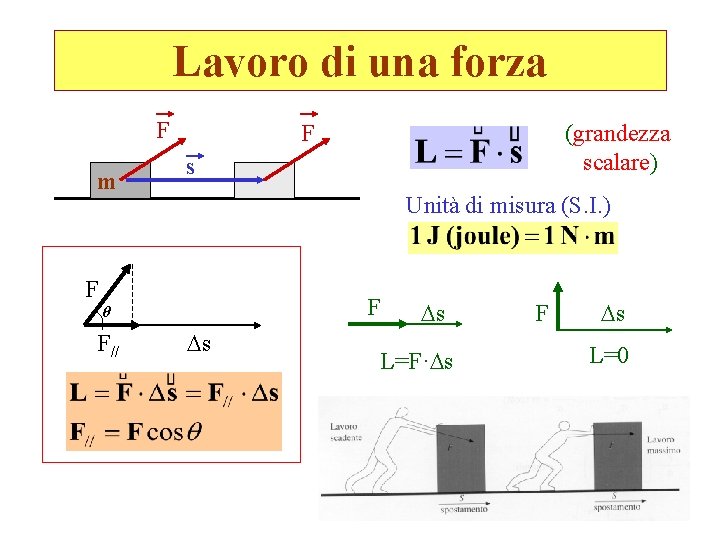
Lavoro di una forza F m F s Unità di misura (S. I. ) F F θ F// (grandezza scalare) s s L=F· s F s L=0

Energia • Rappresenta la capacità che un corpo ha di compiere lavoro. • Concetto comune a molti campi della fisica, può presentarsi in molteplici forme: • energia associata a un corpo in movimento (energia cinetica) • energia associata alla posizione di un corpo (energia potenziale) • energia di legame molecolare (energia chimica) • energia associata alla massa (energia nucleare, E=mc 2) • energia termica e calore • . . • Ogni processo naturale coinvolge trasformazioni di energia. • In un sistema isolato l’energia totale si conserva sempre (principio di conservazione dell’energia).

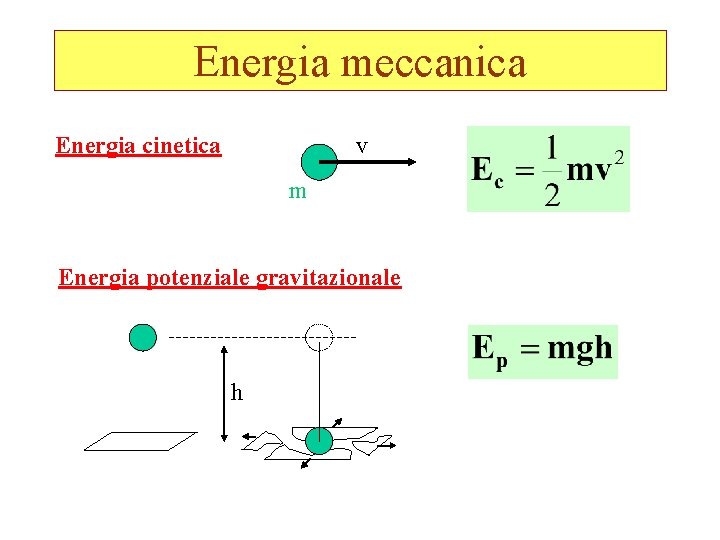
Energia meccanica Energia cinetica v m Energia potenziale gravitazionale h

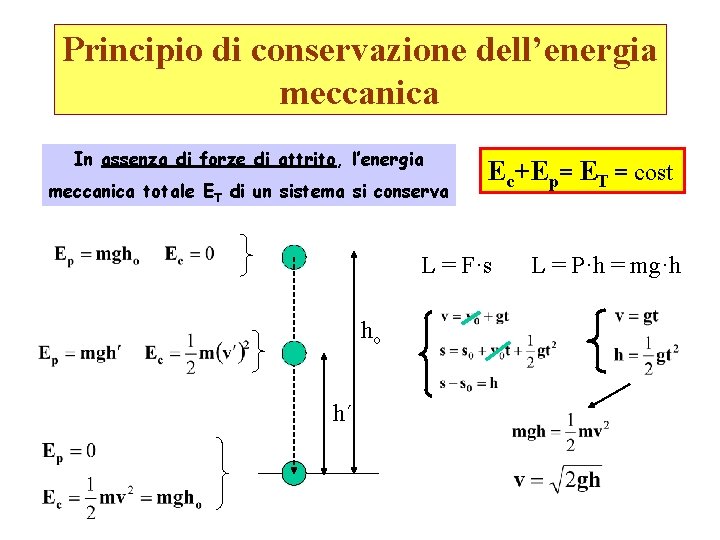
Principio di conservazione dell’energia meccanica In assenza di forze di attrito, l’energia meccanica totale ET di un sistema si conserva Ec+Ep= ET = cost L = F·s ho h´ L = P·h = mg·h

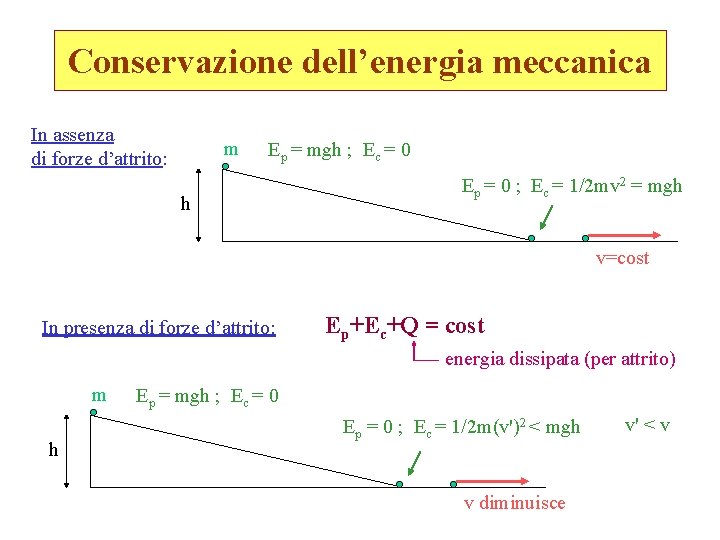
Conservazione dell’energia meccanica In assenza di forze d’attrito: m Ep = mgh ; Ec = 0 h Ep = 0 ; Ec = 1/2 mv 2 = mgh v=cost In presenza di forze d’attrito: Ep+Ec+Q = cost energia dissipata (per attrito) m h Ep = mgh ; Ec = 0 Ep = 0 ; Ec = 1/2 m(v')2 < mgh v diminuisce v' < v

Potenza meccanica La potenza rappresenta il lavoro compiuto da una forza nell’unità di tempo Unità di misura (S. I. ): Esempio: ENEL: Potenza installata: 3 k. W=3· 103 W Si pagano: k. Wh 1 k. Wh = 103 W· 3600 s = = 103 W· 3, 6· 103 s = = 3, 6· 106 W·s = 3, 6· 106 J

Rendimento η di una macchina Macchina: sistema che trasforma energia di vario genere in lavoro meccanico. Nel corpo umano: i muscoli energia chimica lavoro meccanico Rendimento: rapporto tra il lavoro meccanico utile prodotto dalla macchina e l’energia ET impiegata dalla macchina: <1 Esempio: Lutile=25 J η = 20% = 0, 20 = 20/100 Econsumata totale = Lutile/η = 25/0, 2 = 125 J

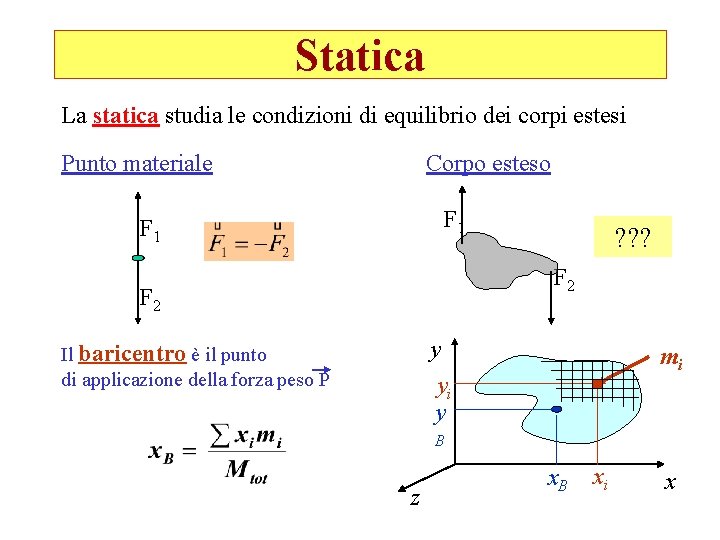
Statica La statica studia le condizioni di equilibrio dei corpi estesi Punto materiale Corpo esteso F 1 ? ? ? F 2 y yi y Il baricentro è il punto di applicazione della forza peso P mi B z x. B xi x

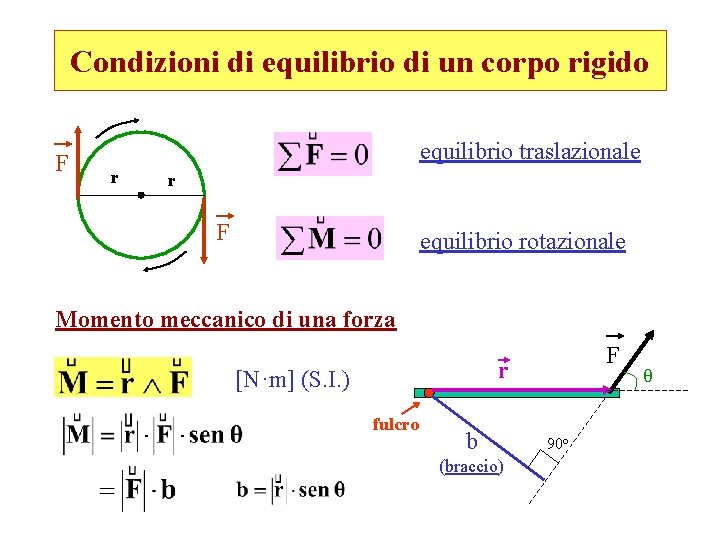
Condizioni di equilibrio di un corpo rigido F equilibrio traslazionale r r F equilibrio rotazionale Momento meccanico di una forza F r [N·m] (S. I. ) fulcro b (braccio) 90 o θ

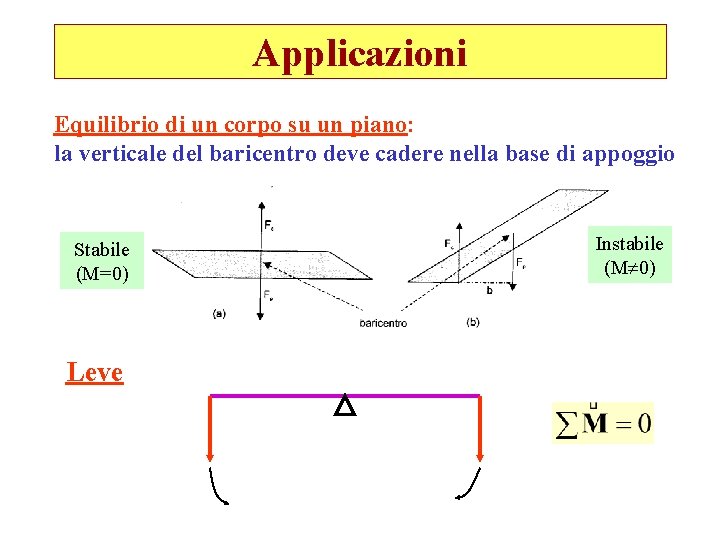
Applicazioni Equilibrio di un corpo su un piano: la verticale del baricentro deve cadere nella base di appoggio Stabile (M=0) Leve Instabile (M 0)

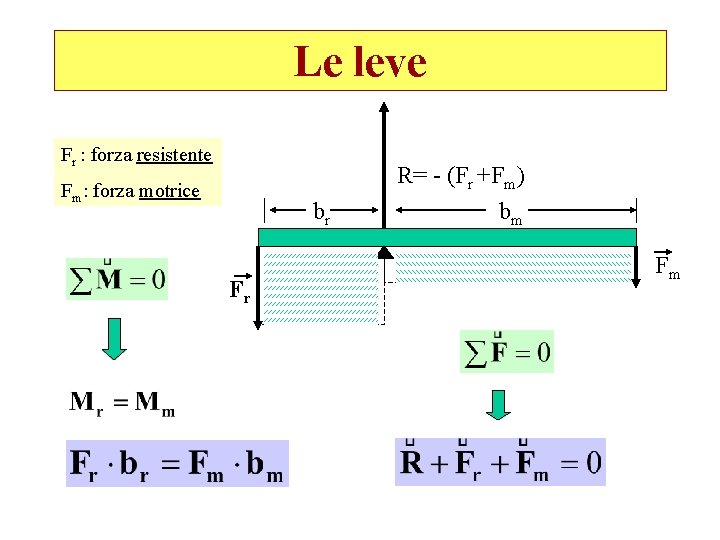
Le leve Fr : forza resistente Fm: forza motrice br Fr R= - (Fr +Fm) bm Fm

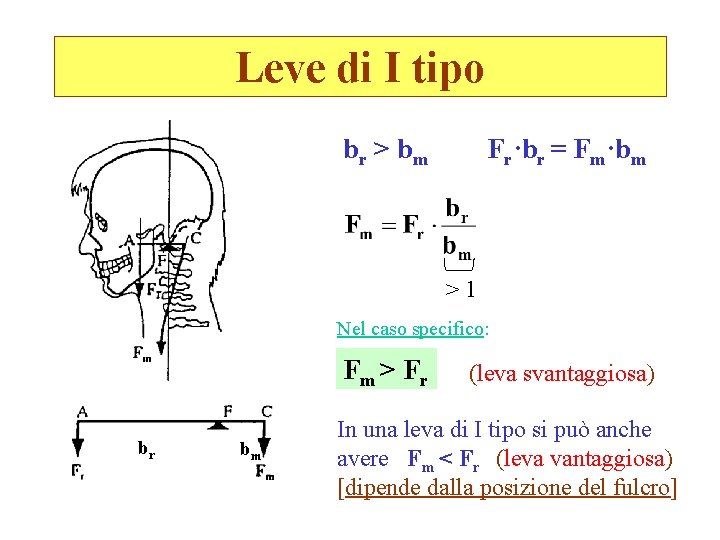
Leve di I tipo br > b m Fr·br = Fm·bm >1 Nel caso specifico: Fm > F r br bm (leva svantaggiosa) In una leva di I tipo si può anche avere Fm < Fr (leva vantaggiosa) [dipende dalla posizione del fulcro]

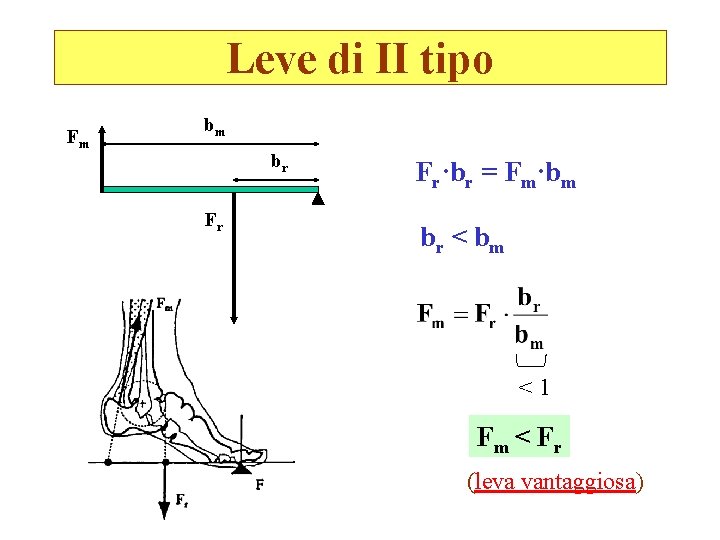
Leve di II tipo Fm bm br Fr Fr·br = Fm·bm br < b m <1 Fm < F r (leva vantaggiosa)

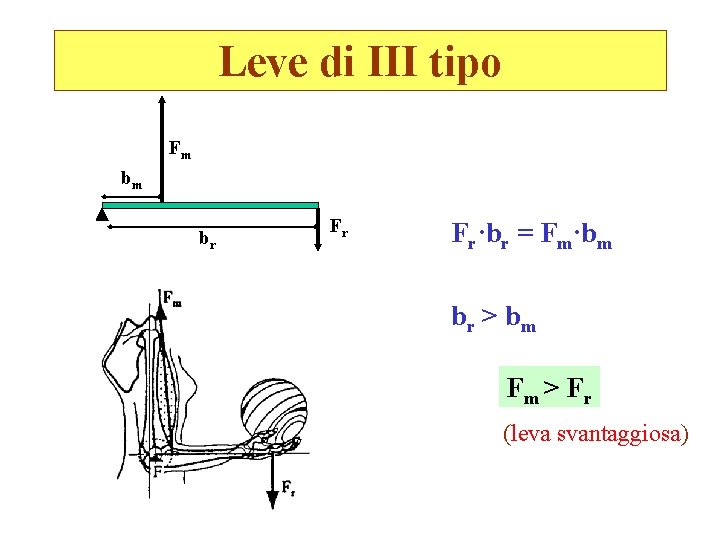
Leve di III tipo Fm bm br Fr Fr·br = Fm·bm br > b m Fm > F r (leva svantaggiosa)

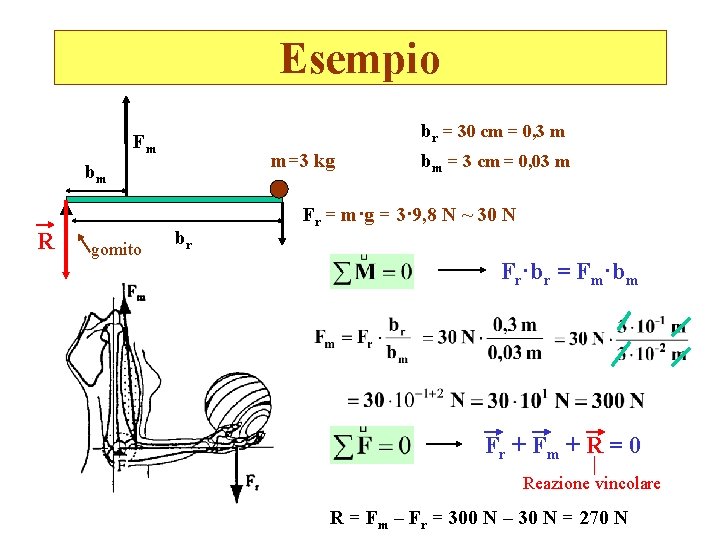
Esempio br = 30 cm = 0, 3 m Fm m=3 kg bm R gomito br bm = 3 cm = 0, 03 m Fr = m·g = 3· 9, 8 N ~ 30 N Fr·br = Fm·bm Fr + F m + R = 0 Reazione vincolare R = Fm – Fr = 300 N – 30 N = 270 N