MECANIQUE DES STRUCTURES PREMIERE PARTIE Analyses au second

MECANIQUE DES STRUCTURES PREMIERE PARTIE Analyses au second ordre J-M Franssen Notes en collaboration avec Prof. R. Maquoi & J-P Jaspart 1

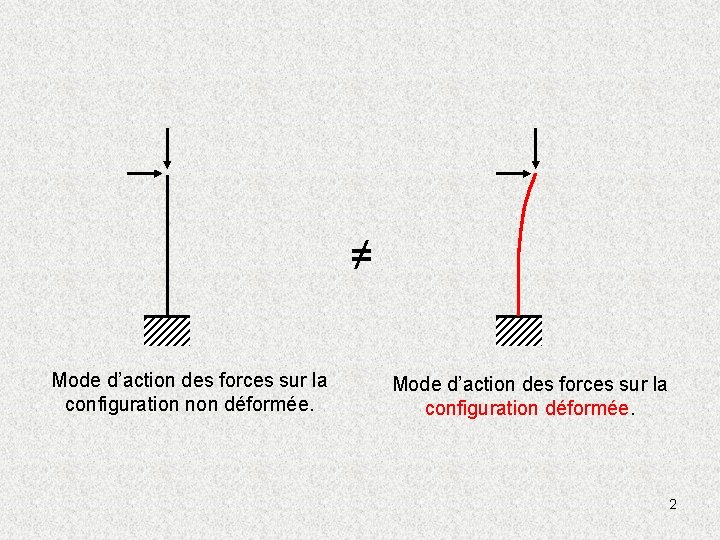
≠ Mode d’action des forces sur la configuration non déformée. Mode d’action des forces sur la configuration déformée. 2

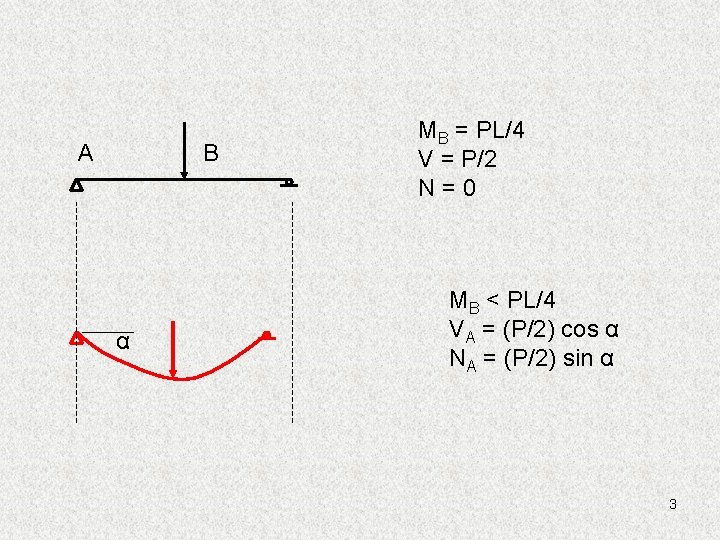
A B α MB = PL/4 V = P/2 N=0 MB < PL/4 VA = (P/2) cos α NA = (P/2) sin α 3

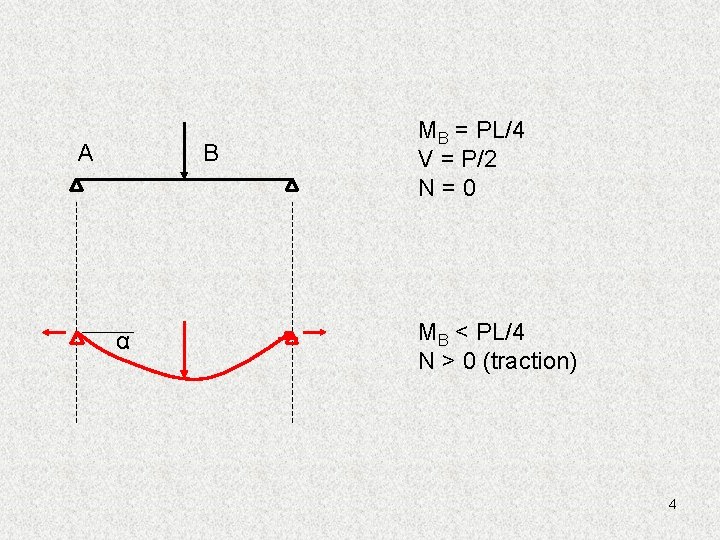
A B α MB = PL/4 V = P/2 N=0 MB < PL/4 N > 0 (traction) 4

Elastique Plastique 1 er ordre 7 premières leçons 2ème ordre Aujourd'hui 5

1. Méthodes d'analyse itératives 1. Globale 2. Partielle 2. Méthode d'analyse directe 3. Evaluation des charges critiques d'instabilité élastique linéaire 6

Analyse au 2ème ordre Détermination des efforts intérieurs SII qui assurent l'équilibre avec les charges extérieures dans la configuration déformée de la structure Analyse au 1 er ordre Détermination des efforts intérieurs SI qui assurent l'équilibre avec les charges extérieures dans la configuration initiale de la structure 7

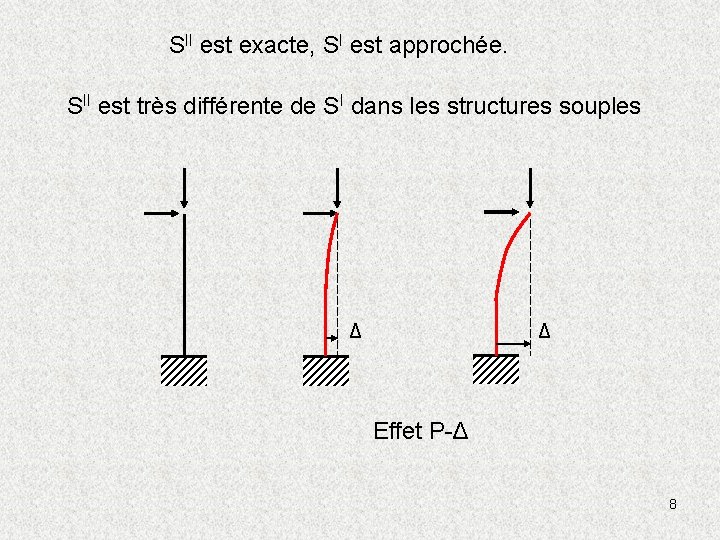
SII est exacte, SI est approchée. SII est très différente de SI dans les structures souples Δ Δ Effet P-Δ 8

Sollicitations S, déplacements v Méthode itérative partielle SI v. I(SI) ΔS 1(v. I) Δv 2(ΔS 1) ΔS 2(Δv 2) Δv 3(ΔS 2) ΔS 3(Δv 3) Δv 4(ΔS 3) ΔS 4(Δv 4) etc Convergence assurée si N < Ncrit SII SI+Σi ΔSi v. II v. I+Σi Δvi !!! Les erreurs ne se répercutent pas 9

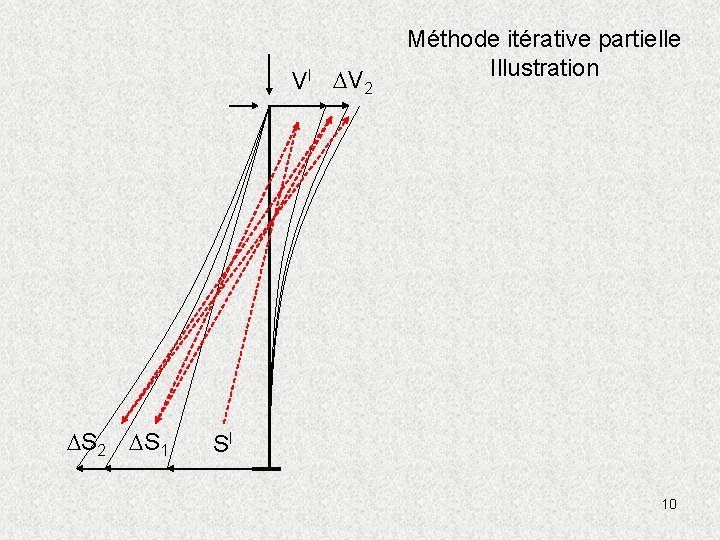
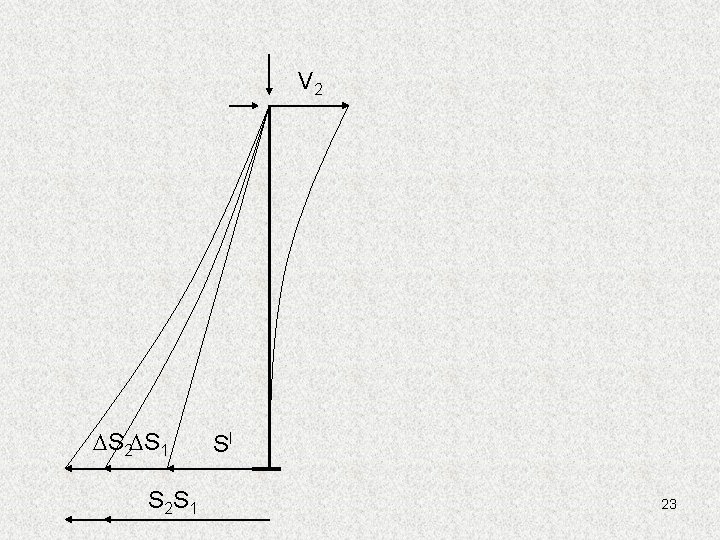
VI DV 2 DS 1 Méthode itérative partielle Illustration SI 10

Exemple: méthode itérative partielle 510 k. N 15 k. N B 9000 EI = A Détermination de SI NI = 510 k. N MI = 15 (h-x) M 1 A = 135 k. Nm x 11

Exemple: méthode itérative partielle 510 k. N 15 k. N NI = 510 k. N MI = 15 (h-x) B 9000 EI = 38. 37 E 6 A Détermination de v. I(SI) x y 1 B = 95 mm 12

Exemple: méthode itérative partielle 510 k. N 15 k. N NI = 510 k. N MI = 15 (h-x) B 9000 EI = 38. 37 E 6 A Détermination de ΔS 1 x 13

Exemple: méthode itérative partielle 510 k. N 15 k. N B 9000 EI = 38. 37 E 6 A Détermination de Δy 1 B (Théorème de la force unité) x Note: en fait, il faudrait calculer Δy 1(x) qui serait en x 5. 14

Exemple: méthode itérative partielle 510 k. N 15 k. N B 9000 EI = 38. 37 E 6 A x A titre d'approximation, on va supposer que Δy 1(x) est parabolique avec une valeur maximale de 40. 96 mm 15

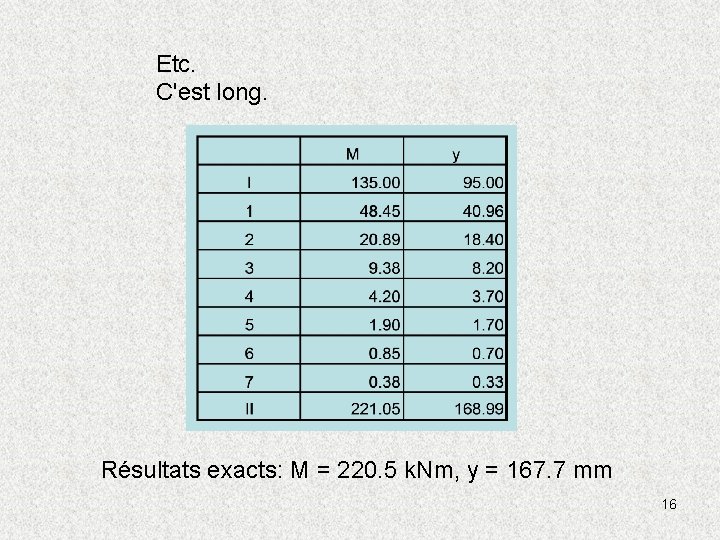
Etc. C'est long. Résultats exacts: M = 220. 5 k. Nm, y = 167. 7 mm 16

17

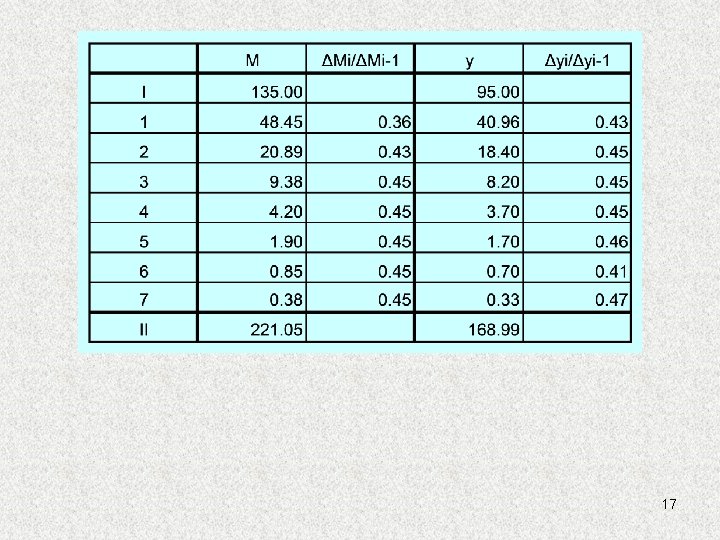
En fait, dépend de x. On choisit en un point particulier (moment à l'encastrement, déplacement à mi-travée). Si on observe 1 = 2 = … = n = , alors; 18

(1) Autre forme de la même formule: (1 b) On peut simplifier en posant 0 = 1 = (2) 19

1: SII = 135 + 48. 45 (1/(1 -0. 43)) = 220 1 b: SII = 135 (1 + 0. 36/(1 -0. 43) ) = 220 2 avec 1 : SII = 135/(1 -0. 43) = 237 2 avec 0 : SII = 135/(1 -0. 36) = 211 20

Sollicitations S, déplacements v Méthode itérative globale SI v. I(SI) ΔS 1(v. I) S 1 = SI+ ΔS 1(v. I) v 2(S 1) ΔS 2(v 2) S 2 = SI+ ΔS 2(v 2) v 3(S 2) ΔS 3(v 3) S 3 = SI+ ΔS 3(v 3) v 4(S 3) ΔS 4(v 4) etc Convergence assurée si N < Ncrit SII SI+ΔSn v. II Vn !!! Les erreurs se répercutent de pas en pas 21

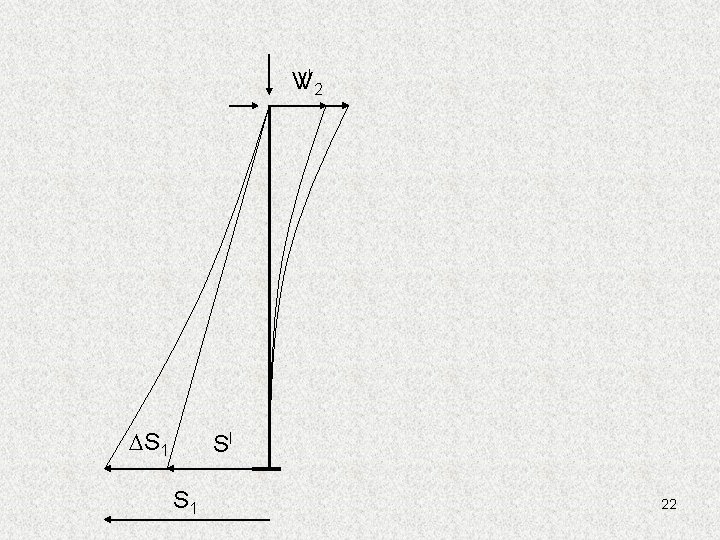
VVI 2 DS 1 SI S 1 22

V 2 DS 2 DS 1 S 2 S 1 SI 23

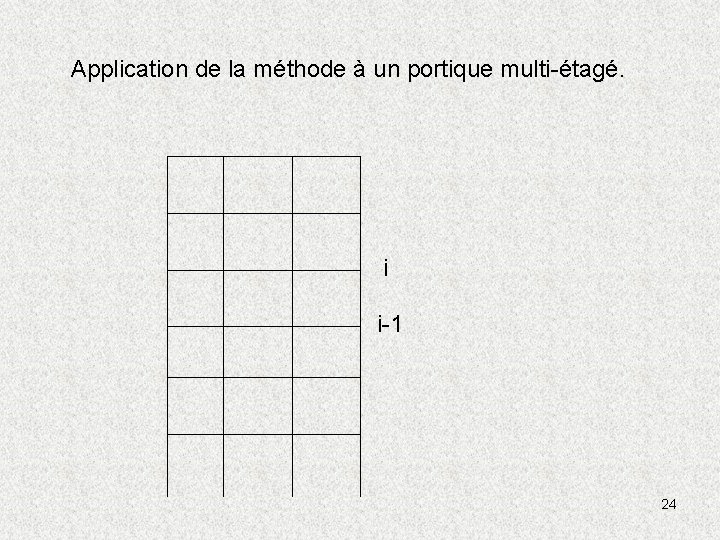
Application de la méthode à un portique multi-étagé. i i-1 24

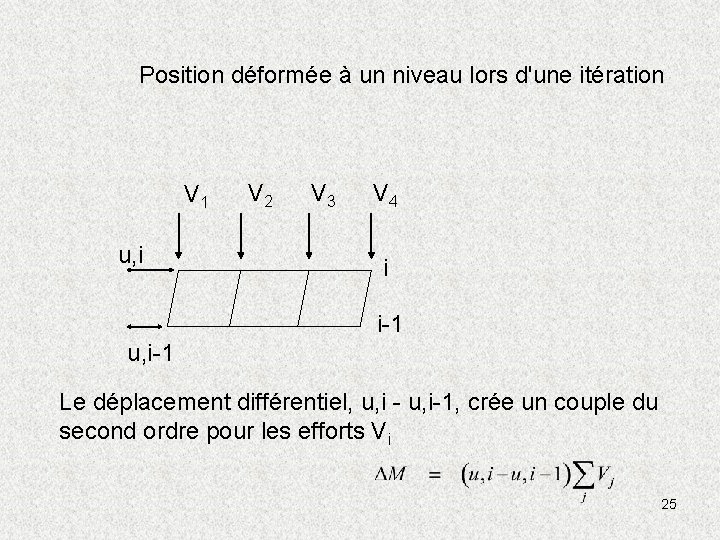
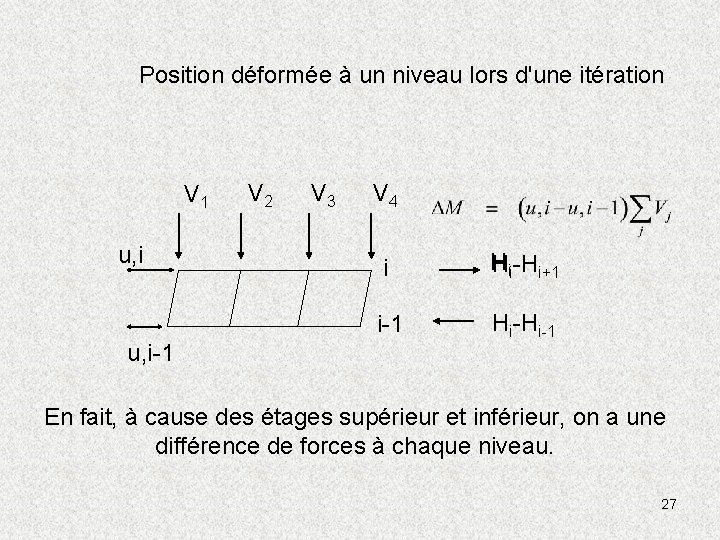
Position déformée à un niveau lors d'une itération V 1 u, i V 2 V 3 V 4 i i-1 u, i-1 Le déplacement différentiel, u, i - u, i-1, crée un couple du second ordre pour les efforts Vi 25

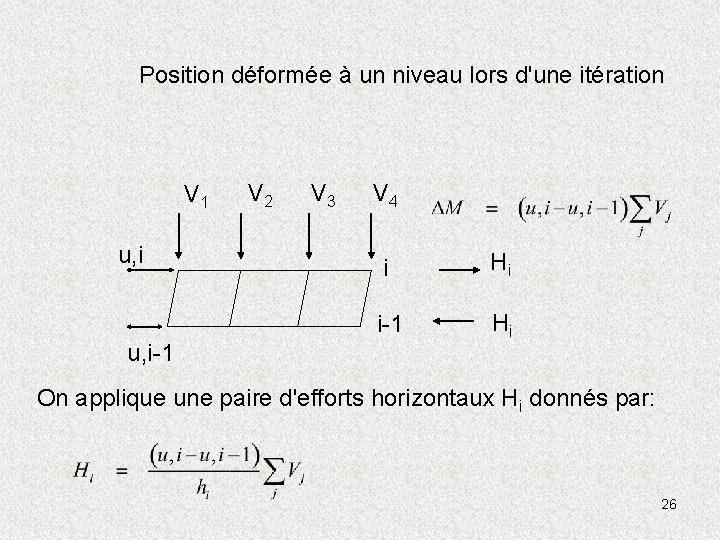
Position déformée à un niveau lors d'une itération V 1 u, i-1 V 2 V 3 V 4 i Hi i-1 Hi On applique une paire d'efforts horizontaux Hi donnés par: 26

Position déformée à un niveau lors d'une itération V 1 u, i-1 V 2 V 3 V 4 i Hii-Hi+1 i-1 Hi-Hi-1 En fait, à cause des étages supérieur et inférieur, on a une différence de forces à chaque niveau. 27

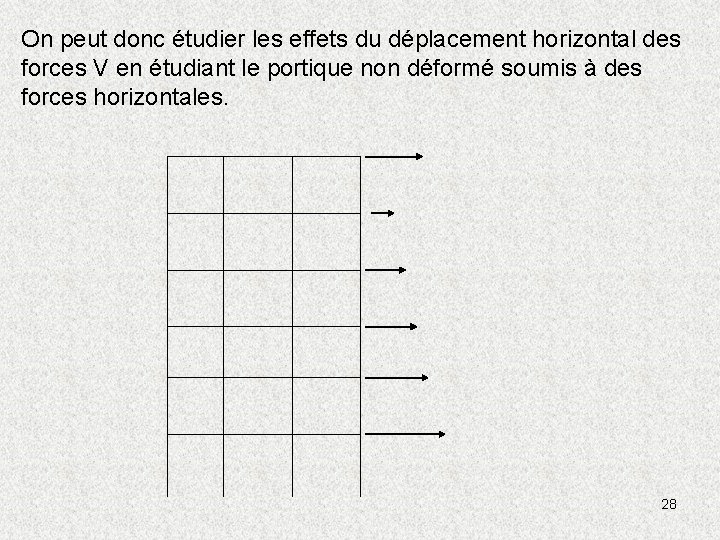
On peut donc étudier les effets du déplacement horizontal des forces V en étudiant le portique non déformé soumis à des forces horizontales. 28

Charge critique élastique linéaire On suppose un état de référence libre de toute flexion. Donc v. I = SI = 0 On ne peut donc avoir instabilité (et v. II 0 et SII 0) que si = 1 En pratique, pour déterminer , on démarre avec une déformée de flexion estimée 29

Exemple: colonne bi-articulée Déformée de flexion estimée: (intégration de v'' = -M/EI) donne 30

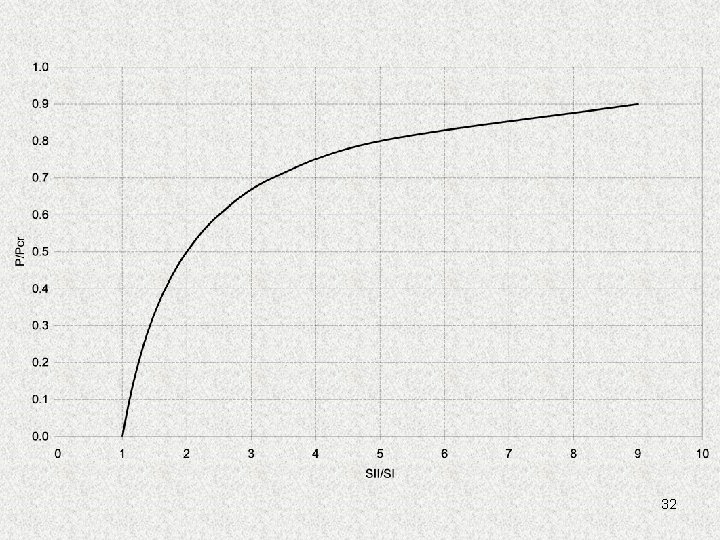
donne donc une mesure de l'éloignement vis-à-vis de la charge critique. Si est petit, P est éloigné de Pcr. Si est proche de 1, P est proche de Pcr. devient => Si on connaît Pcr (et P, bien entendu), on peut avoir une bonne estimation des sollicitations et des déformations au 31 second ordre.

32

Méthode directe Rappel de la méthode des rotations appliquée à un portique multi-étagé Dans chaque barre, on a: Mg = mg + 2 EI/L ( 2Φg+Φd-3ψ) Md = md + 2 EI/L ( 2Φd+Φg-3ψ) avec M: moments d'extrémités dans la barre m: moments d'encastrement parfaits Φ: rotations des nœuds ψ: déviation de la corde de la barre 33

Dans chaque barre, on a: Mg = mg + 2 EI/L ( 2Φg+Φd-3ψ) Md = md + 2 EI/L ( 2Φd+Φg-3ψ) A chaque nœud, on a Σi Mi + Mext = 0 A chaque étage, on a: 34