MECANIQUE APPLIQUEE STATIQUE Principe fondamental de la statique

MECANIQUE APPLIQUEE STATIQUE Principe fondamental de la statique

Généralités LA STATIQUE C’EST L’ETUDE DE L’EQUILIBRE DES CORPS En statique les solides sont supposés : Géométriquement parfaits : Les aspérités et les défauts de formes, les états de surfaces, ne sont pas pris en compte. Les surfaces sont modélisées par des plans, des cylindres… Indéformables : On ne tient pas compte des déformations sous les efforts. Homogènes : Même masse volumique partout (kg. m-3) Isotropes : Chaque morceau de matière a le même comportement dans toutes les directions (contre exemple : le bois assure une meilleure résistance dans le sens des fibres que dans le sens perpendiculaire aux fibres).

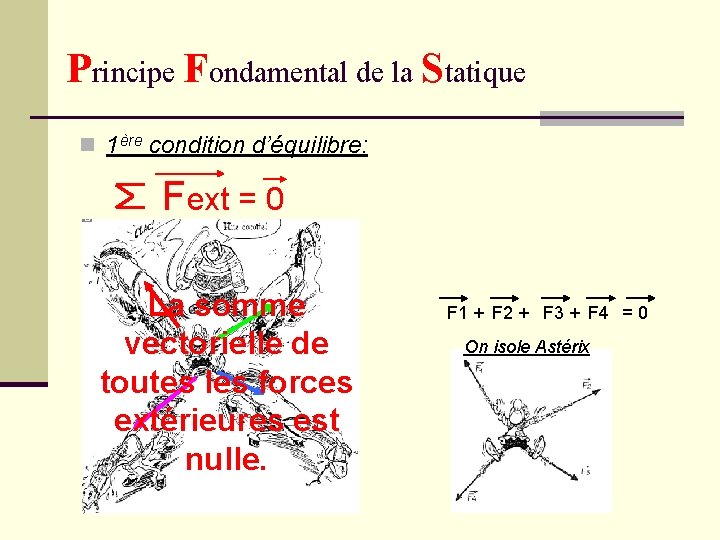
Principe Fondamental de la Statique n 1ère condition d’équilibre: Fext = 0 La somme vectorielle de toutes les forces extérieures est nulle. F 1 + F 2 + F 3 + F 4 = 0 On isole Astérix

Principe Fondamental de la Statique n 2ème condition d’équilibre: Mi(F ext) =0 Mi (F 1) + Mi (F 2) = 0 ou Mi (F 1) = - Mi (F 2) LE MOMENT RESULTANT EN UN MEME POINT DE TOUTES LES FORCES EXTERIEURES EST NULLE.

Principe Fondamental de la Statique n. Vérification: Un moment est une force multipliée par une distance. La distance se mesure du point d’application de la force jusqu’au point I. On prend d 1 = d 2 = 1 mètre Les poids des personnages sont identiques: on prend 700 N Mi (F 1) = F 1 x d 1 Mi (F 2) = F 2 x (-d 2) Mi(F 1)+Mi(F 2)= (F 1 xd 1)+(F 2 x(-d 2))= (700 x 1)+(700 x(-1))= 700 -700= 0 CONDITION D’EQUILIBRE VERIFIEE

CAS PARTICULIERS n Solide soumis à l’action de 2 forces Un solide soumis à l’action de 2 forces reste en équilibre si les 2 forces sont égales et opposées. (Même direction et intensité mais sens opposé) On isole Astérix: Équilibre si: F 1 + F 2 = 0 Donc F 1 = - F 2

CAS PARTICULIERS n Solide soumis à l’action de 3 forces dont 2 //: Un solide soumis à l’action de 3 forces coplanaires dont 2 sont // est en équilibre si la 3ème force est // au 2 autres. On isole Astérix: Équilibre si: F 1 + F 2 + F 3 = 0 ou F 3 = - ( F 1 + F 2)

CAS PARTICULIERS n Solide soumis à l’action de 3 forces concourantes: Un solide soumis à l’action de 3 forces coplanaires et concourantes est en équilibre si: Les 3 forces sont se coupent en un même point I. On isole Astérix: Équilibre si: F 1 + F 2 + F 3 = 0

Exercices Vérifier la condition d’équilibre des différentes sommes de vecteurs forces suivantes : F 1 + + F 3 F 2

Exercices Vérifier la condition d’équilibre des différentes sommes de vecteurs forces suivantes : F 1 + F 2

Exercices Vérifier la condition d’équilibre des différentes sommes de vecteurs forces suivantes : F 1 F 2 + F 3 +

Exercices Vérifier la condition d’équilibre des différentes sommes de vecteurs forces suivantes : F 1 + F 2 + F 3

Exercices Vérifier la condition d’équilibre des différentes sommes de vecteurs forces suivantes : F 2 F 1 +

Exercices 4. 2 – Déterminer les inconnues pour que les conditions d’équilibre soient vérifiées : ? 500 N F 1 0. 8 0. 5 Calculs : F 2

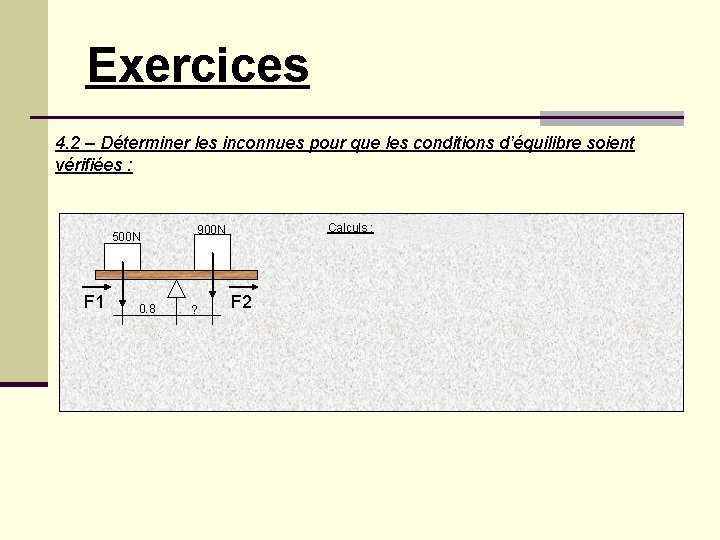
Exercices 4. 2 – Déterminer les inconnues pour que les conditions d’équilibre soient vérifiées : 500 N F 1 0. 8 Calculs : 900 N ? F 2

Exercices 4. 2 – Déterminer les inconnues pour que les conditions d’équilibre soient vérifiées : F 1 0. 8 Calculs : ? 500 N 0. 3 F 2

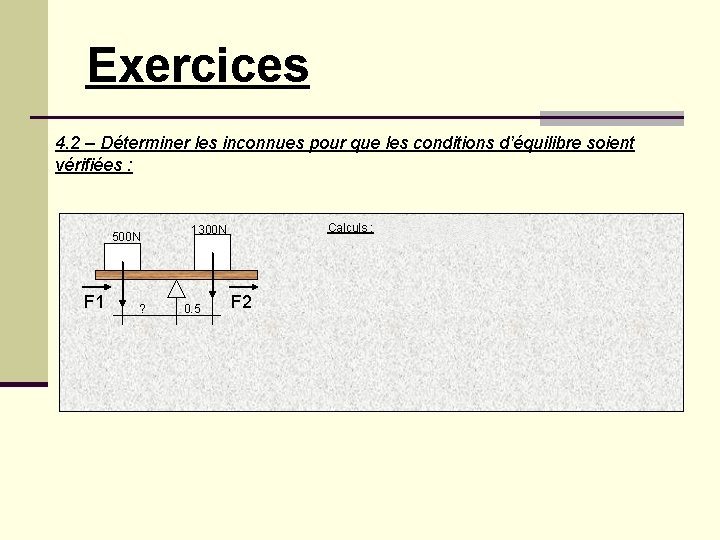
Exercices 4. 2 – Déterminer les inconnues pour que les conditions d’équilibre soient vérifiées : 500 N F 1 ? Calculs : 1300 N 0. 5 F 2