Measuring the Stability of Feature Selection Sarah Nogueira

Measuring the Stability of Feature Selection Sarah Nogueira and Gavin Brown sarah. nogueira@manchester. ac. uk School of Computer Science University of Manchester

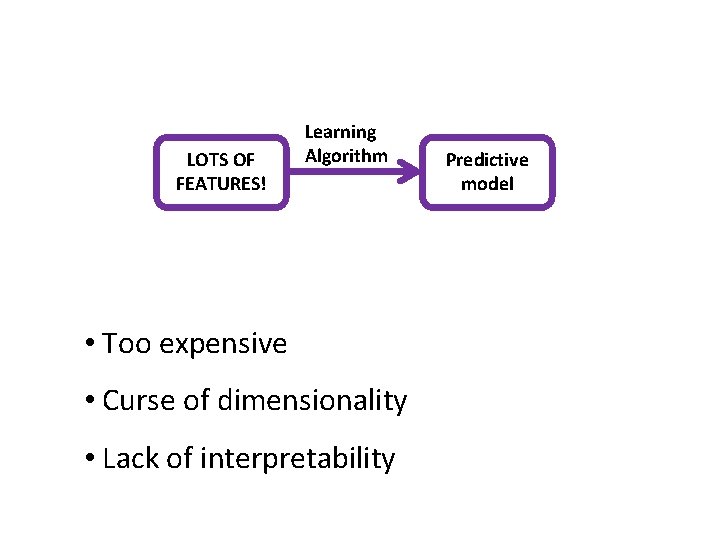
LOTS OF FEATURES! Learning Algorithm • Too expensive • Curse of dimensionality • Lack of interpretability Predictive model

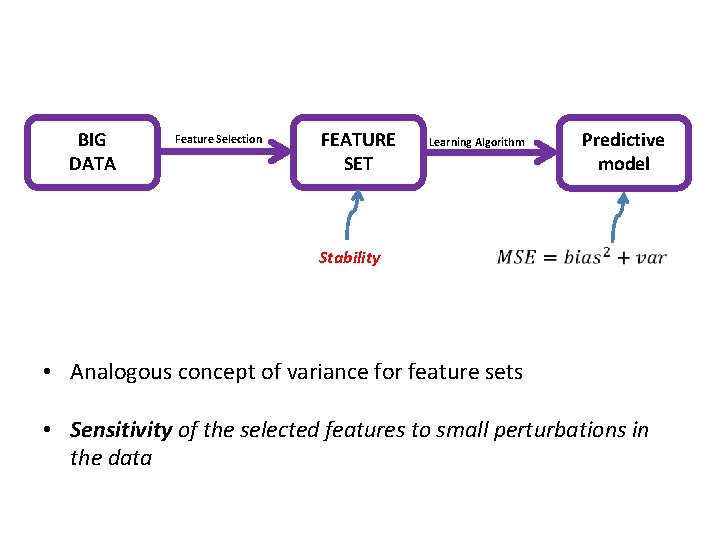
BIG DATA Feature Selection FEATURE SET Stability Learning Algorithm Predictive model • Analogous concept of variance for feature sets • Sensitivity of the selected features to small perturbations in the data

Stability A recent and growing area of research • Indicator of reproducible research • In biomarker identification - stability is said to be as important as predictive power - Instability has been a major obstacle to clinical applications

Literature to quantify stability! Jaccard (2002) POG (2006) Hamming (2007) Kuncheva (2007) Krizek (2007) Dice (2008) n. POG (2009) Lustgarten (2009) CWrel (2010) Wald (2013) Lots of definitions Some statistical, some heuristics Conflicting opinions Different use cases

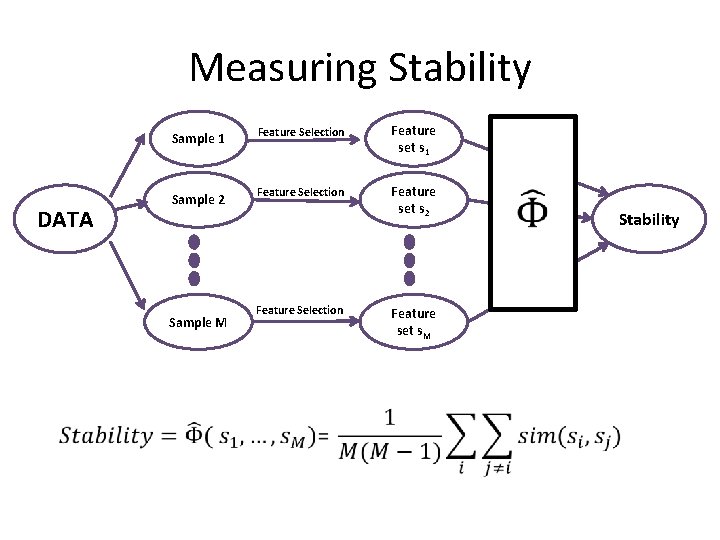
Measuring Stability Sample 1 DATA Sample 2 Sample M Feature Selection Feature set s 1 Feature Selection Feature set s 2 Feature Selection Feature set s. M Stability

What properties/behaviours should a measure have, such that values are interpretable and comparable? Jaccard (2002) Dice (2008) POG (2006) n. POG (2009) Hamming (2007) Lustgarten (2009) Kuncheva (2007) CWrel (2010) Krizek (2007) Wald (2013)

Imagine we had d features…. binary string of length d. 11100 Select features 1, 2, 3 00101 Select features 3, 5

Imagine we had d features…. binary string of length d. 11100 10110 00111. . 11010 Select EXACTLY 3 features, M times. Binary matrix M x d

Desirable property 1: Fully defined 11100 00111. . 10010 Sometimes select 2. Sometimes select 3. Not all measures work in this scenario!

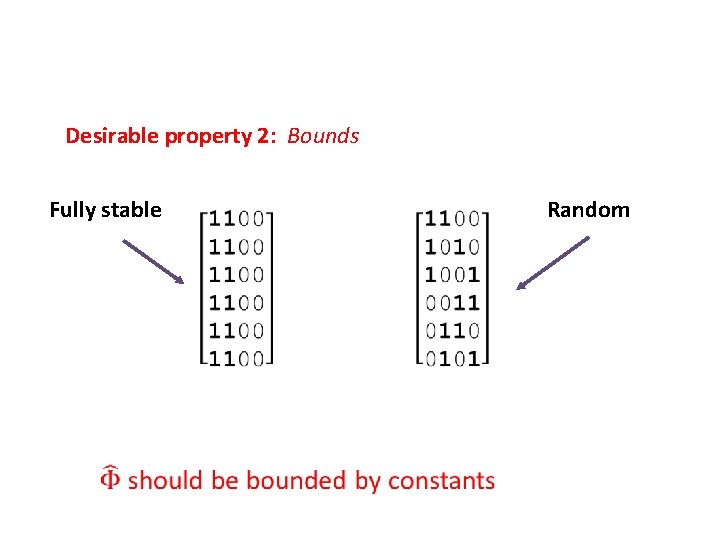
Desirable property 2: Bounds Fully stable Random

Desirable property 3: Maximum Lustgarten (2009) measure

Desirable property 3: Maximum

Desirable property 4: Correction for chance 1 1 000……………… 00 000 110

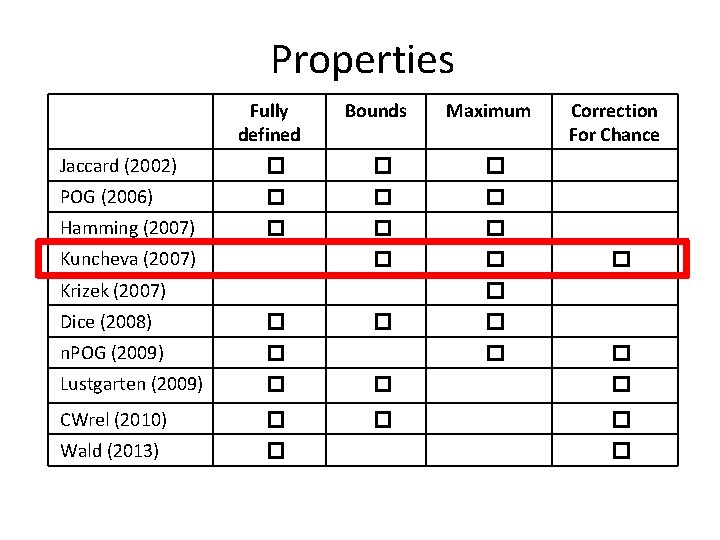
Properties Fully defined Bounds Maximum Jaccard (2002) � � � POG (2006) � � � Hamming (2007) � � � Kuncheva (2007) Krizek (2007) Correction For Chance � � Dice (2008) � n. POG (2009) � Lustgarten (2009) � � � CWrel (2010) � � � Wald (2013) � � �

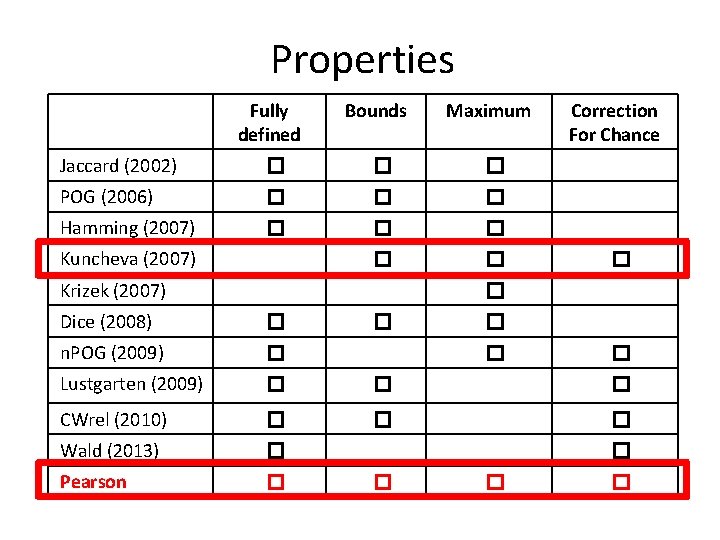
Properties Fully defined Bounds Maximum Jaccard (2002) � � � POG (2006) � � � Hamming (2007) � � � Kuncheva (2007) Krizek (2007) Correction For Chance � � Dice (2008) � n. POG (2009) � Lustgarten (2009) � � � CWrel (2010) � � � Wald (2013) � Pearson � � � � �

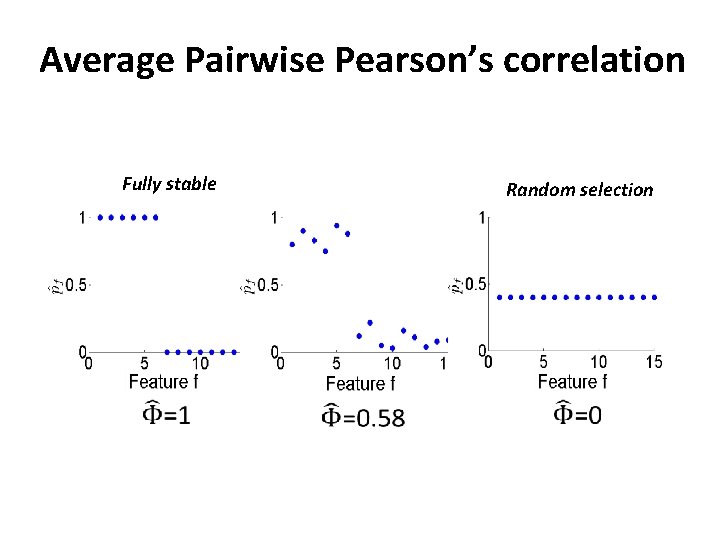
Average Pairwise Pearson’s correlation Fully stable Random selection

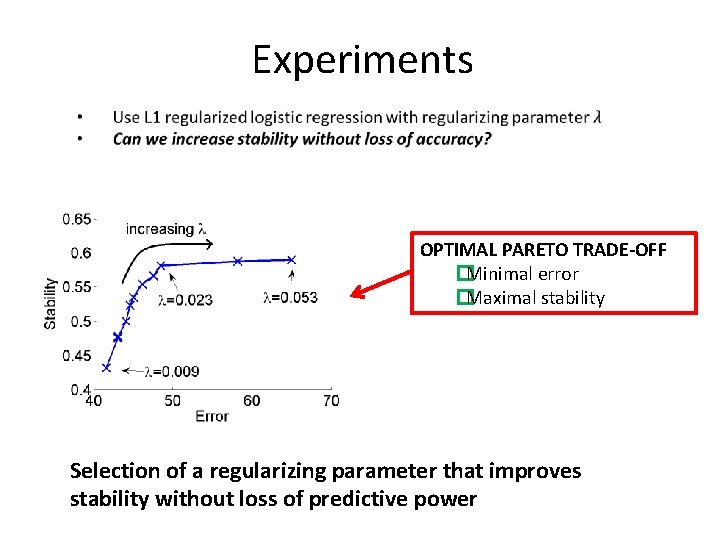
Experiments OPTIMAL PARETO TRADE-OFF �Minimal error �Maximal stability Selection of a regularizing parameter that improves stability without loss of predictive power

Conclusions Increasing stability brings more confidence in the features selected in the model. Pearson’s correlation can do the job, having all desirable properties. Implementation in Matlab available online at: https: //github. com/nogueirs/ECML 2016

Thank you