Measuring Angles Section 1 3 Unit 1 ANGLE

Measuring Angles Section 1. 3 Unit 1

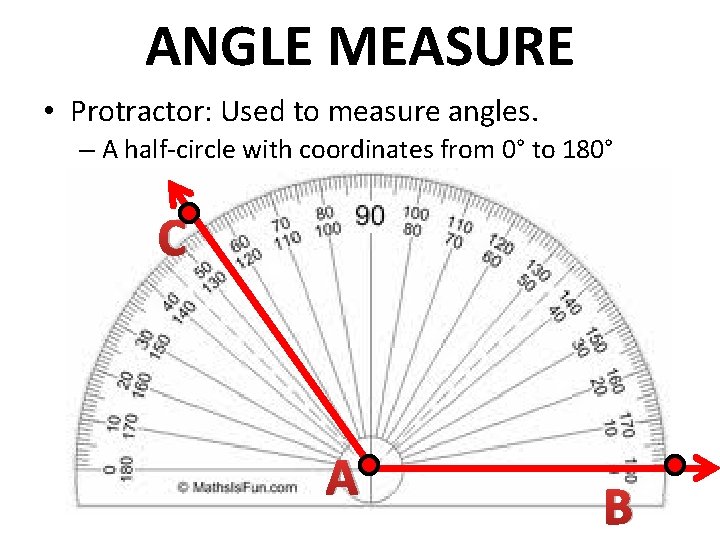
ANGLE MEASURE • Protractor: Used to measure angles. – A half-circle with coordinates from 0° to 180° C A B

How to use a protractor: • 1. Put the center of the protractor at the vertex. • 2. Align the protractor so that ray AB passes through 0 on the protractor. • 3. Read the measure of the angle (in degrees) at the point where ray AC intersects the scale on the protractor

C A B Why isn’t the measure of the angle 55 degrees instead of 125 degrees?

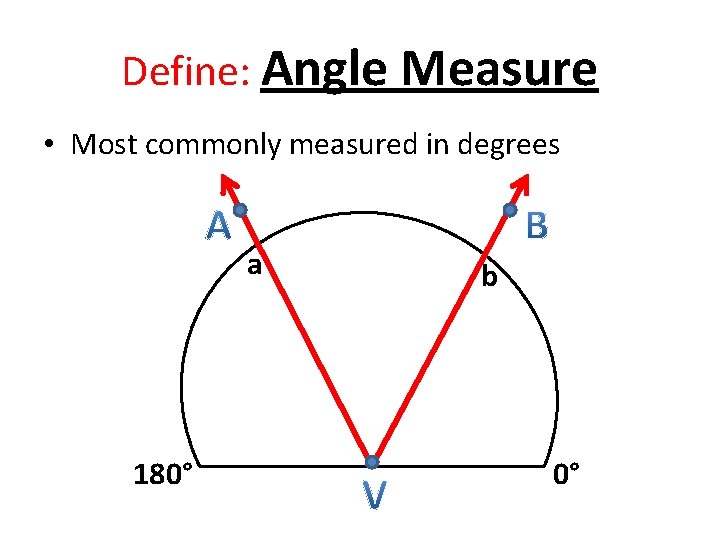
Define: Angle Measure • Most commonly measured in degrees a 180° b 0°

Definition: Measure of an Angle • Suppose that the vertex, V, of <AVB is placed on the center point of a half-circle with coordinates from 0° to 180° so that and intersect the half-circle. Let a & b be the coordinates of the intersections. • Then, the measure of the angle, written as <AVB, is or

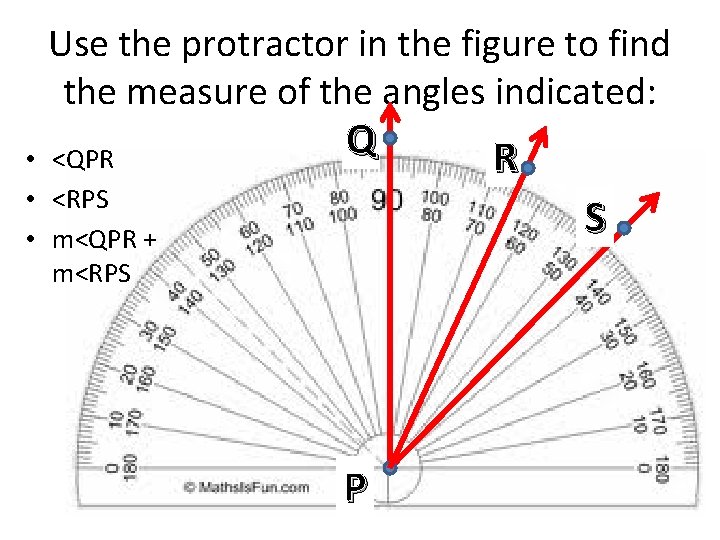
Use the protractor in the figure to find the measure of the angles indicated: • <QPR • <RPS • m<QPR + m<RPS Q R S P

Congruent Angles • Congruent if one can be moved onto the other so that they match exactly. • Tick marks are used to show which angles are known to be congruent • NOTE: Angles are said to match if their sides match. The length of the sides do not matter.

ANGLE CONGRUENCE POSTULATE • If 2 angles have the same measure, then they are congruent. • If 2 angles are congruent, then they have the same measure. • If m<ABC = m<DEF, then _______ • If <ABC <DEF, then ________

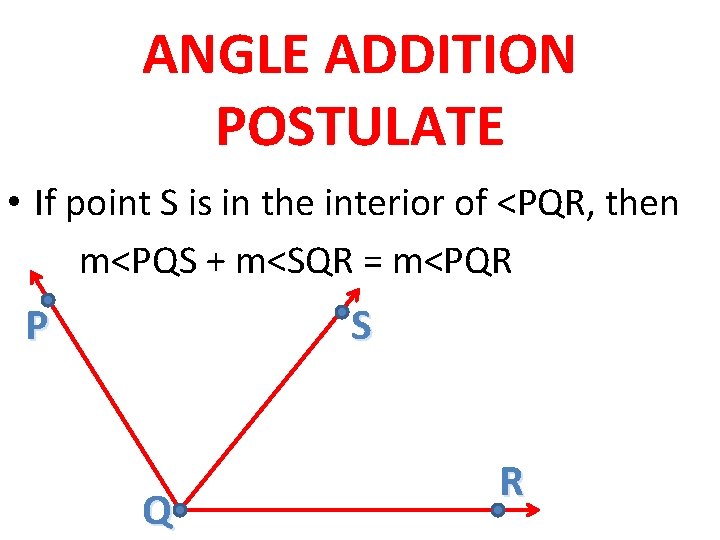
ANGLE ADDITION POSTULATE • If point S is in the interior of <PQR, then m<PQS + m<SQR = m<PQR P S Q R

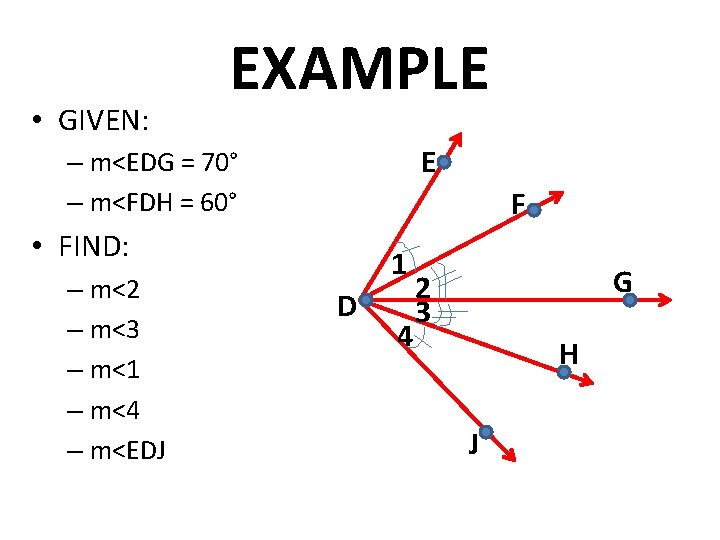
• GIVEN: EXAMPLE E – m<EDG = 70° – m<FDH = 60° F • FIND: – m<2 – m<3 – m<1 – m<4 – m<EDJ 1 D 4 G 2 3 H J

SPECIAL ANGLE PAIRS • Complementary Angles: – 2 angles whose measures have a sum of 90°. – Each angle is called the complement of the other. • Supplementary Angles: – 2 angles whose measures have a sum of 180°. – Each angle is called the supplement of the other.

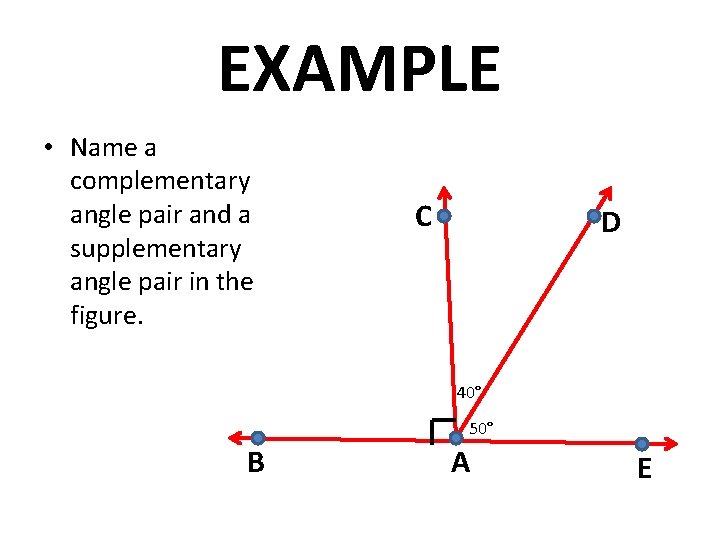
EXAMPLE • Name a complementary angle pair and a supplementary angle pair in the figure. C D 40° 50° B A E

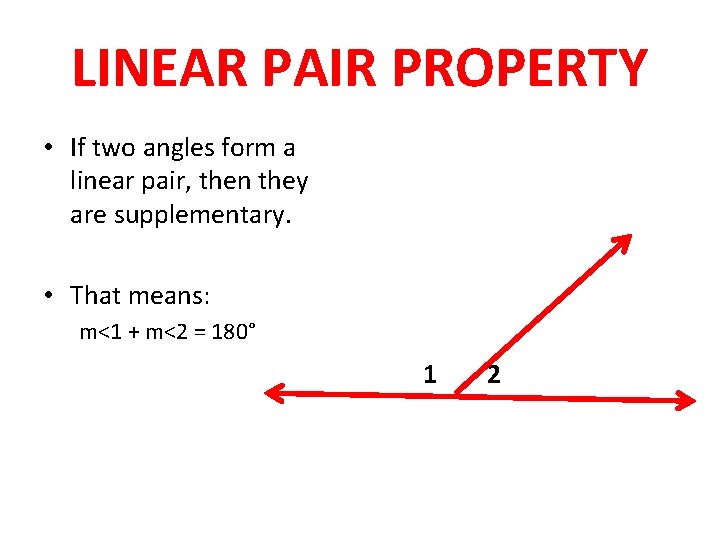
DEFINITION: LINEAR PAIR • If the endpoint of a ray falls on a line so that two angles are formed, then the angles are known as a Linear Pair. 1 2

LINEAR PAIR PROPERTY • If two angles form a linear pair, then they are supplementary. • That means: m<1 + m<2 = 180° 1 2

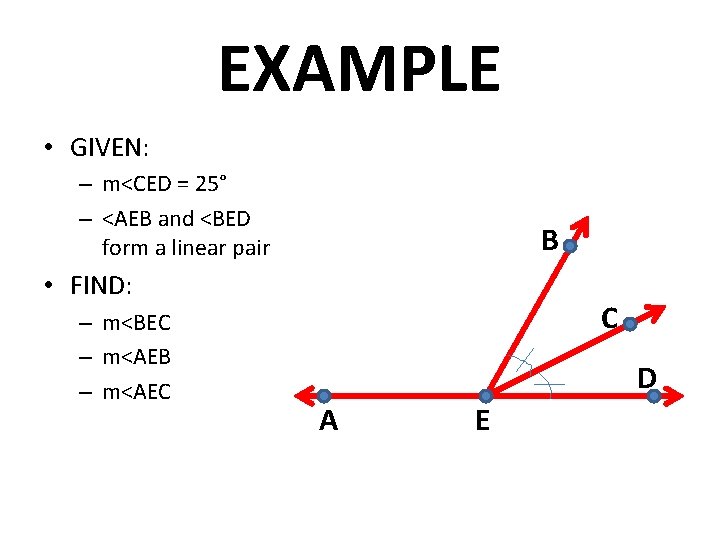
EXAMPLE • GIVEN: – m<CED = 25° – <AEB and <BED form a linear pair B • FIND: – m<BEC – m<AEB – m<AEC C D A E

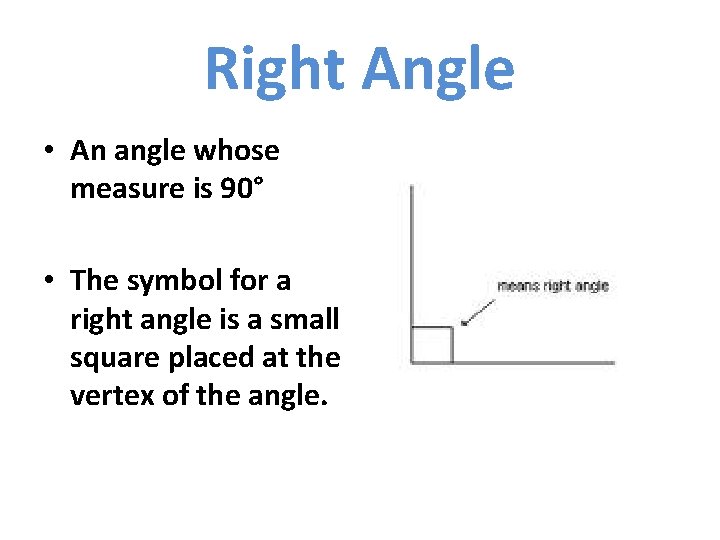
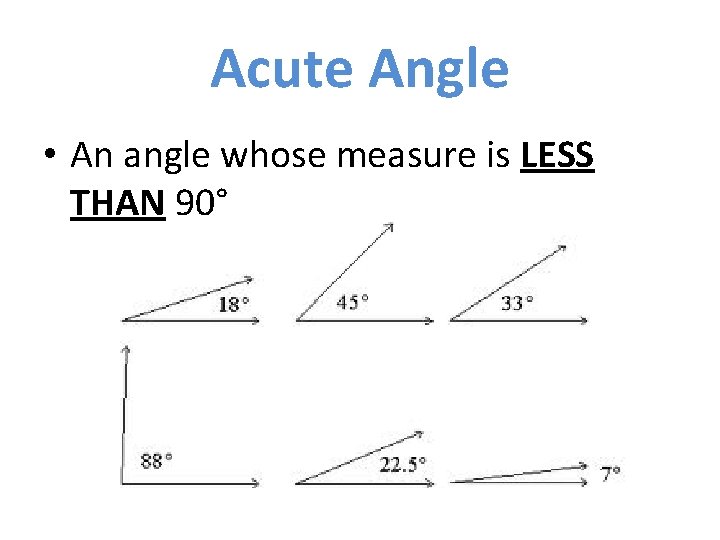
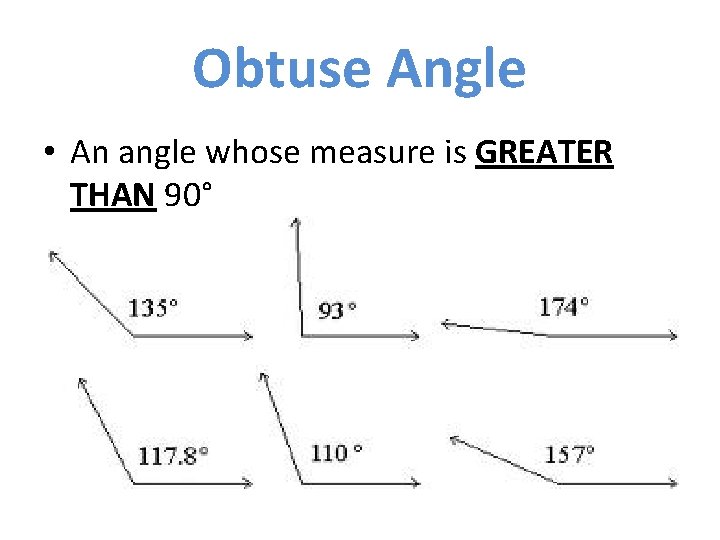
CLASSIFICATION OF ANGLES • Classified according to their measure. • 3 different types of angles: – Right angle – Acute angle – Obtuse angle

Right Angle • An angle whose measure is 90° • The symbol for a right angle is a small square placed at the vertex of the angle.

Acute Angle • An angle whose measure is LESS THAN 90°

Obtuse Angle • An angle whose measure is GREATER THAN 90°