Measuring angle 3 Super Bfactory Sanjay Kumar Swain

Measuring angle 3/ @Super B-factory Sanjay Kumar Swain University of Hawaii • What is the angle 3 ? • Methods to measure 3 DCPK(*)Dcsd. K D(KS )K D(*) K • Conclusion

CKM matrix (Wolfenstein parameterization) Wolfenstein parameterization
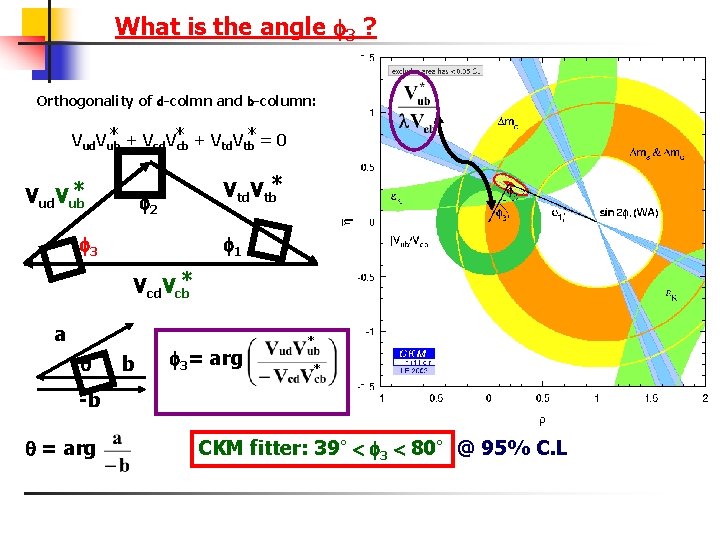
What is the angle 3 ? Orthogonality of d-colmn and b-column: * + V V * = 0 Vud. Vub cd cb td tb 2 � 3 1 Vcd. Vcb* a � Vtd. Vtb* � � * Vud. Vub b 3= arg * * -b = arg CKM fitter: 39° 3 80° @ 95% C. L

Gronau-London-Wyler method to extract 3 -0 ) B- DCPK- where Dcp (D 0 ± D • Amp(B- DCPK-) = Amp(B- D 0 K-) + Amp(B- D 0 K-)- - K+K-, + - 2 diagrams CP + modes s b - Vcb KS 0, KS ’ D 0 and D 0 u K- b 3=arg(V*ub) D - u u Color-favored ~ Vcb Vub B- c o B- CP - modes - u -o -c D s K- - u u Color-suppressed ~Vub
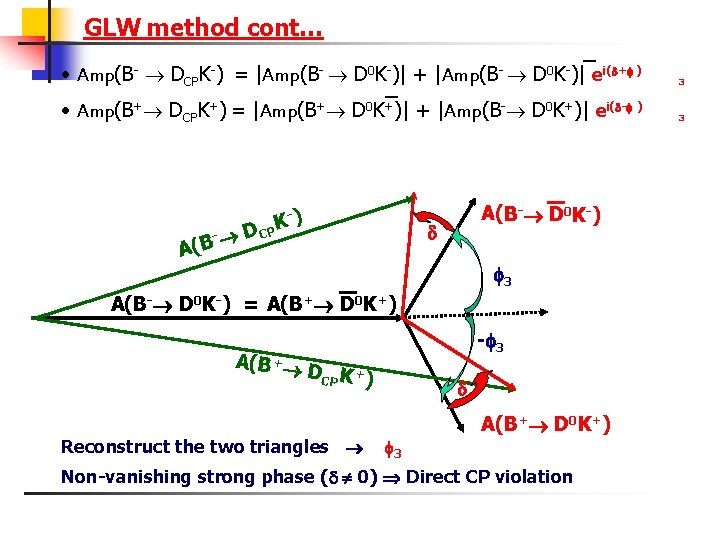
GLW method cont… _ • Amp(B- DCPK-) = |Amp(B- D 0 K-)| + |Amp(B- D 0 K-)| ei( + ) _ • Amp(B+ DCPK+) = |Amp(B+ D 0 K+)| + |Amp(B- D 0 K+)| ei( - ) - A(B -) D CPK — A(B- D 0 K-) 3 — A(B- D 0 K-) = A(B+ D 0 K+) A(B + - 3 DCPK +) Reconstruct the two triangles 3 A(B+ D 0 K+) Non-vanishing strong phase ( 0) Direct CP violation 3 3
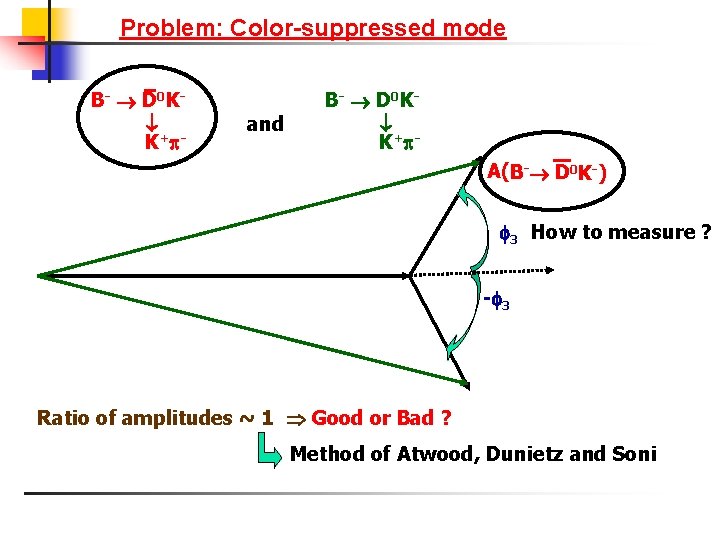
Problem: Color-suppressed mode B- D 0 K K+ - and B- D 0 K K+ - — A(B- D 0 K-) 3 How to measure ? - 3 Ratio of amplitudes ~ 1 Good or Bad ? Method of Atwood, Dunietz and Soni

Theoretical solution One can instead measure: R 1, 2 = RDCP /R Dnon-CP = 1 + r 2 2 r cos( ) 3 where R R 1 + R 2 2 DCP = B (B- D 1, 2 K-) + C. C B (B- D 1, 2 -) + C. C = 2( 1 + r 2) r = |B KD|/|B KD| In principle one can obtain r Useful inequality: Sin 2 3 < R 1, 2 R 1 or R 2 < 1. 0 (assuming small r )
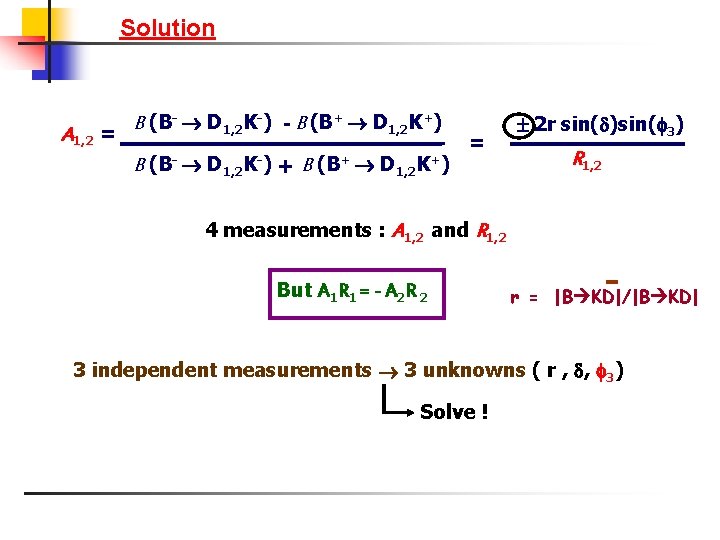
Solution B (B- D 1, 2 K-) - B (B+ D 1, 2 K+) A 1, 2 = = B (B- D 1, 2 K-) + B (B+ D 1, 2 K+) 2 r sin( )sin( 3) R 1, 2 4 measurements : A 1, 2 and R 1, 2 But A 1 R 1 = - A 2 R 2 r = |B KD|/|B KD| 3 independent measurements 3 unknowns ( r , , 3) Solve !
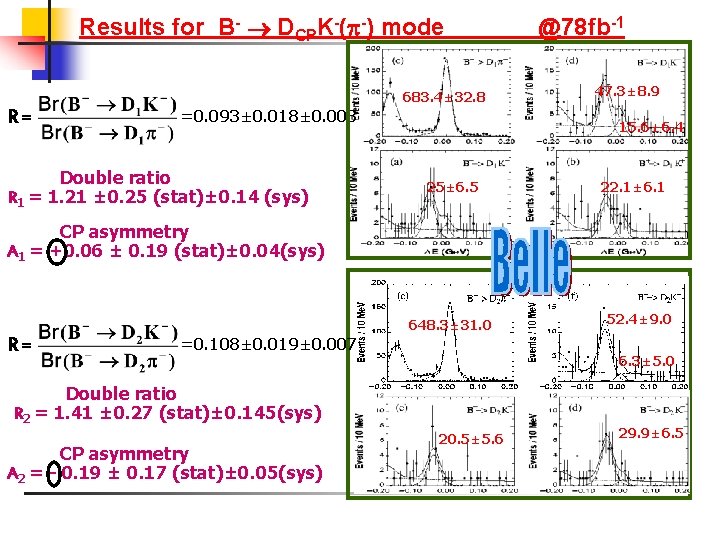
Results for B- DCPK-( -) mode 683. 4± 32. 8 R= =0. 093± 0. 018± 0. 008 Double ratio R 1 = 1. 21 ± 0. 25 (stat)± 0. 14 (sys) @78 fb-1 47. 3± 8. 9 15. 6± 6. 4 25± 6. 5 22. 1± 6. 1 CP asymmetry A 1 = +0. 06 ± 0. 19 (stat)± 0. 04(sys) 648. 3± 31. 0 R= =0. 108± 0. 019± 0. 007 6. 3± 5. 0 Double ratio R 2 = 1. 41 ± 0. 27 (stat)± 0. 145(sys) CP asymmetry A 2 = - 0. 19 ± 0. 17 (stat)± 0. 05(sys) 52. 4± 9. 0 20. 5± 5. 6 29. 9± 6. 5

Measuring 3 using B- DCPK- mode Using the measured value of R 1, 2 and A 1, 2 We find: r 2 = R 1 R 2 = 0. 31 0. 21 r = |B KD|/|B KD| 2 Just 1. 5 away from physical boundary: r 2 =0 otherwise r would be imaginary r is likely to be, r= 0. 1 - 0. 2 ( theory) r 2= 0. 04 @80 fb-1 , r 2=0. 21 At 3 ab-1 , r 2= 0. 034 1 measurement (Super-B factory) Need to find another way to measure “r”
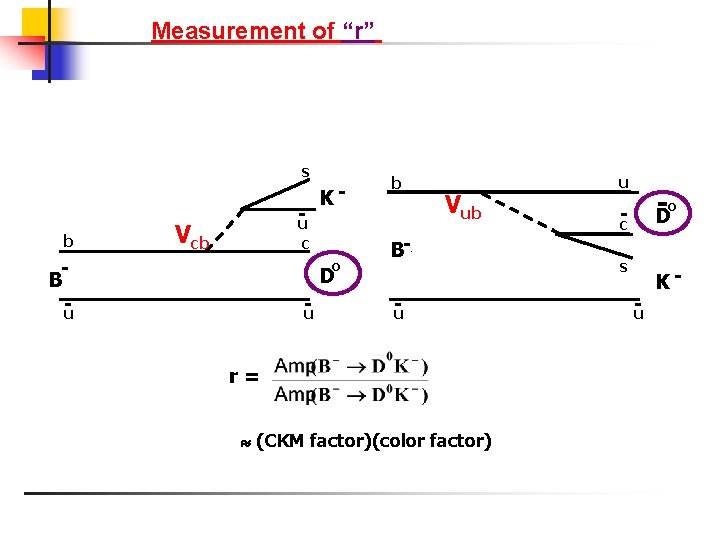
Measurement of “r” s b u Vcb K- c B u o b Vub B- D - u r= (CKM factor)(color factor) u -o -c D s K- - u
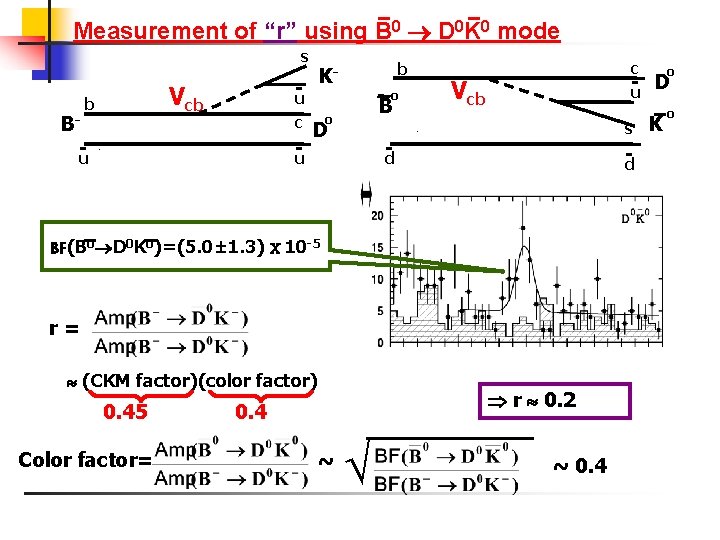
Measurement of “r” using B 0 D 0 K 0 mode s B- -u Vcb b c -u -u b K- o B o D c -u Vcb s -d -d BF(B 0 D 0 K 0)=(5. 0± 1. 3) 10 -5 r= (CKM factor)(color factor) 0. 45 Color factor= r 0. 2 0. 4 ~ ~ 0. 4 o D K o
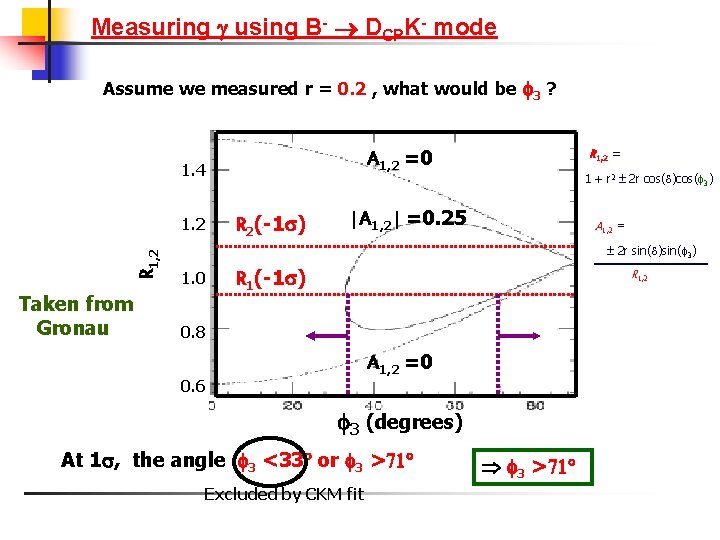
Measuring using B- DCPK- mode Assume we measured r = 0. 2 , what would be 3 ? A 1, 2 =0 1. 4 R 1, 2 1. 2 Taken from Gronau R 2(-1 ) R 1, 2 = 1 + r 2 2 r cos( )cos( 3) |A 1, 2| =0. 25 A 1, 2 = 2 r sin( )sin( 3) 1. 0 R 1(-1 ) R 1, 2 0. 8 A 1, 2 =0 0. 6 3 (degrees) At 1 , the angle 3 <33 or 3 > Excluded by CKM fit 3 >
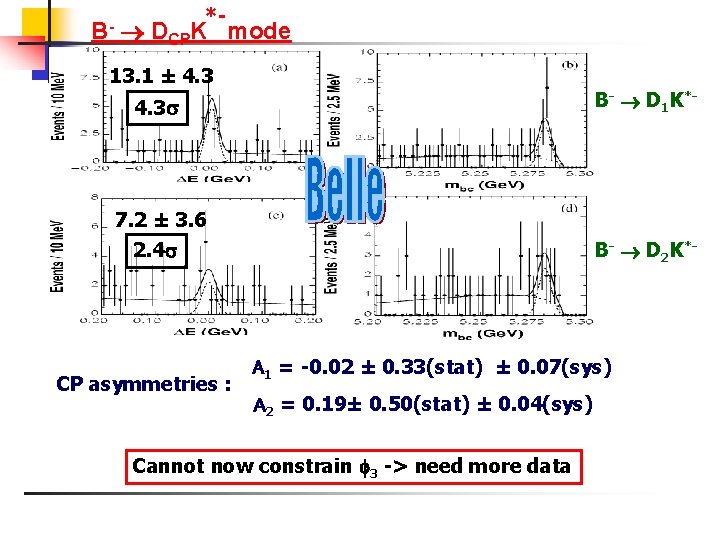
B- *- DCPK mode 13. 1 ± 4. 3 B- D 1 K*- 7. 2 ± 3. 6 2. 4 B- D 2 K*- CP asymmetries : A 1 = -0. 02 ± 0. 33(stat) ± 0. 07(sys) A 2 = 0. 19± 0. 50(stat) ± 0. 04(sys) Cannot now constrain 3 -> need more data
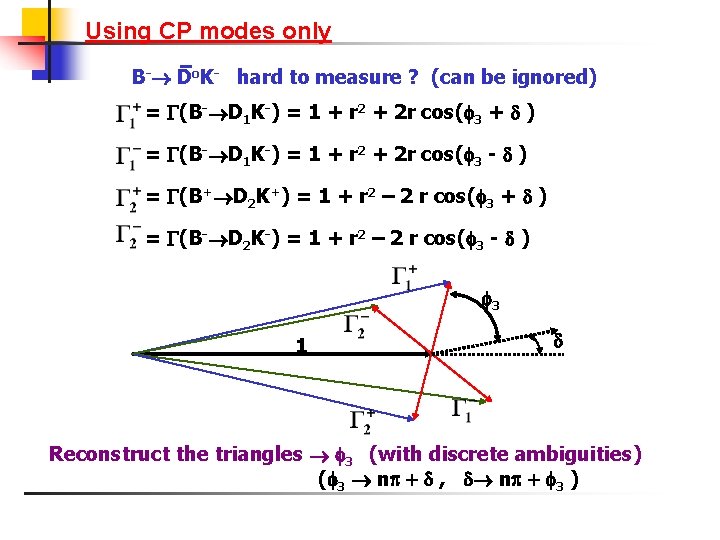
Using CP modes only B- Do. K- hard to measure ? (can be ignored) = (B- D 1 K-) = 1 + r 2 + 2 r cos( 3 + ) = (B- D 1 K-) = 1 + r 2 + 2 r cos( 3 - ) = (B+ D 2 K+) = 1 + r 2 – 2 r cos( 3 + ) = (B- D 2 K-) = 1 + r 2 – 2 r cos( 3 - ) 3 1 Reconstruct the triangles 3 (with discrete ambiguities) ( 3 n , n 3 )
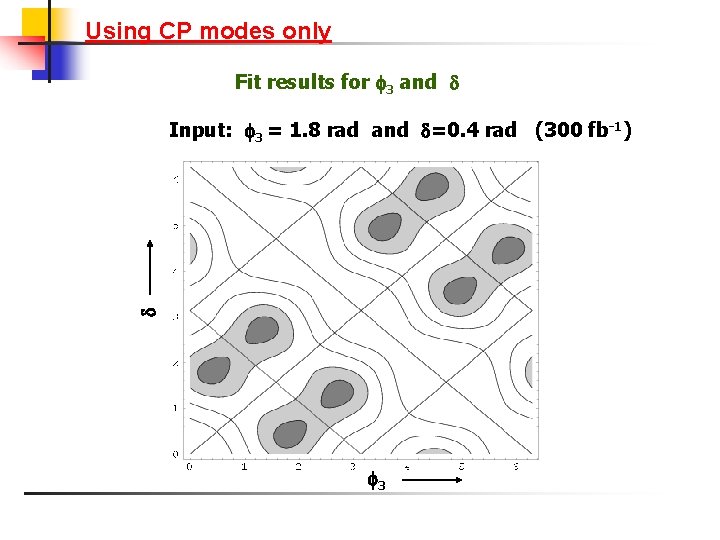
Using CP modes only Fit results for 3 and Input: 3 = 1. 8 rad and =0. 4 rad (300 fb-1) 3
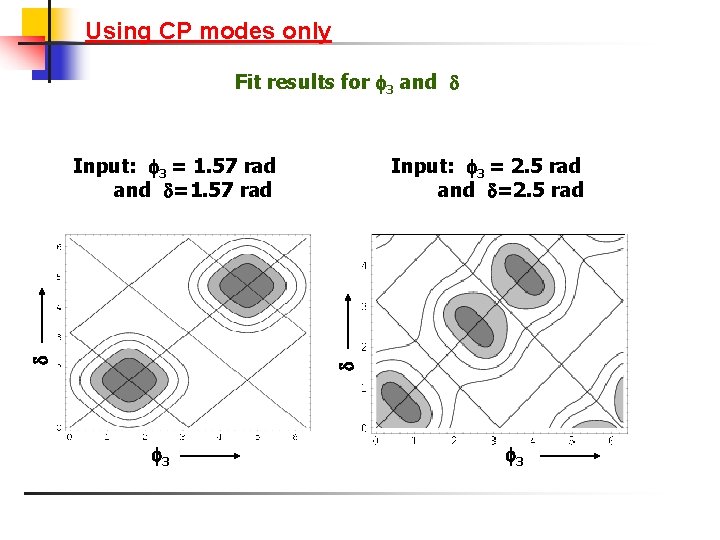
Using CP modes only Fit results for 3 and Input: 3 = 2. 5 rad and =2. 5 rad Input: 3 = 1. 57 rad and =1. 57 rad 3 3
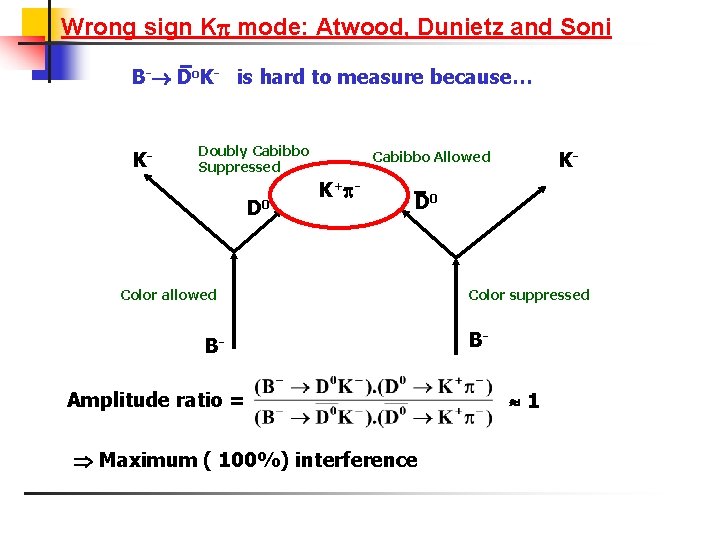
Wrong sign K mode: Atwood, Dunietz and Soni B- Do. K- is hard to measure because… K- Doubly Cabibbo Suppressed D 0 K- Cabibbo Allowed K+ - D 0 Color allowed BAmplitude ratio = Maximum ( 100%) interference Color suppressed B 1

Atwood, Dunietz and Soni method…. . This interference causes maximum CP asymmetry order of unity ( 100%) Measure B- DK- in two decay modes of D: e. g K+ - and KS 0 ( their CP conjugates) [B- (K+ -)K-] [B+ (K- +)K+] [B- (KS 0)K-] [B+ (KS 0)K+] Solve for K , 3 and r + - S 0
![ADS method…. . di: [B- D( fi ) K-] a: [B+ D 0( fi ADS method…. . di: [B- D( fi ) K-] a: [B+ D 0( fi](http://slidetodoc.com/presentation_image_h/1c2b326d3ce053d0d9f729311d733b80/image-20.jpg)
ADS method…. . di: [B- D( fi ) K-] a: [B+ D 0( fi ) K+] di: [B+ D( fi ) K+] b: [B+ D 0( fi ) K+] di ( measured) = di ( 3 , i , b) Eliminate i : Plot 3 vs b : func( 3 -b)=0 One line Two modes intersect: Solution
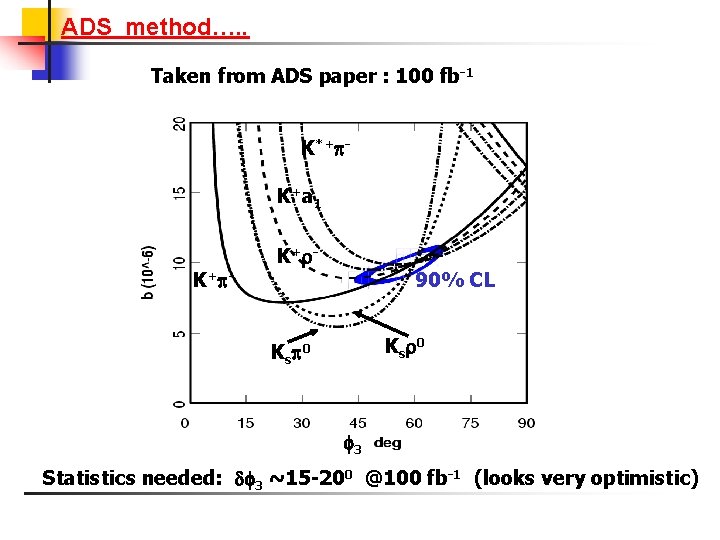
ADS method…. . Taken from ADS paper : 100 fb-1 K*+ K+a 1 K+ - 90% CL Ks 0 3 Statistics needed: 3 ~15 -200 @100 fb-1 (looks very optimistic)
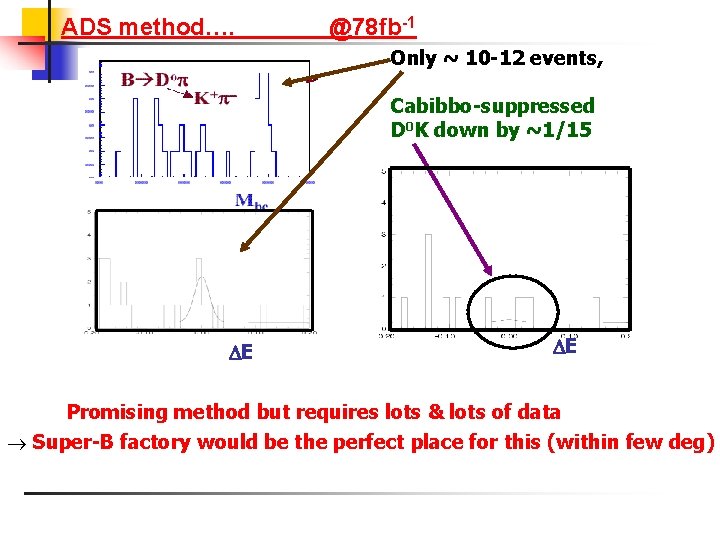
ADS method…. @78 fb-1 Only ~ 10 -12 events, Cabibbo-suppressed D 0 K down by ~1/15 E E Promising method but requires lots & lots of data Super-B factory would be the perfect place for this (within few deg)

B- D 0(KS + -)K- Dalitz analysis Previously: B- DCPK- where DCP =(D 0 ) both D 0 and D 0 decays to CP eigenstates ( K+K-. . ) D 0 K 0 - D KS - 3 ) f(m 2 , m 2 ) Amp(B+ ->DK+) = f(m+2, m-2 ) + r ei( + + where m+/-2= M 2(KS +/-) r = |B KD|/|B KD| f( m+2, m-2) = ak ei Ak(m+2, m-2) + b ei -> both 2 -body resonances and non-res component
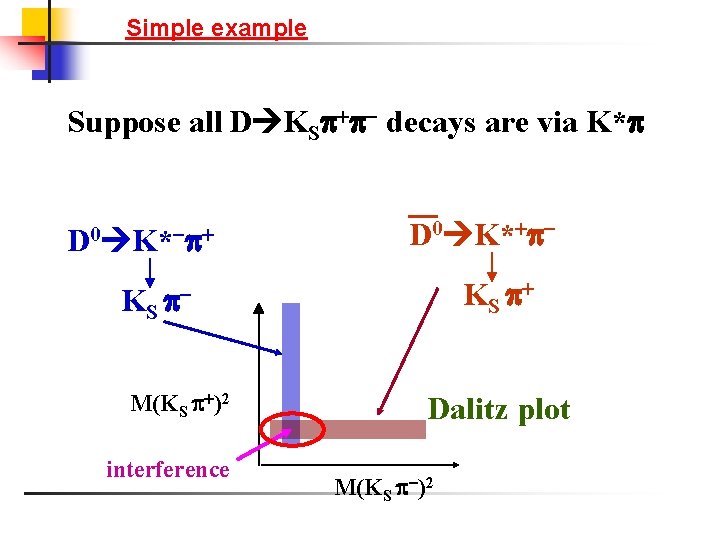
Simple example Suppose all D KS - decays are via K* D 0 K*- D 0 K* - - KS M(KS )2 Dalitz plot KS interference M(KS -)2
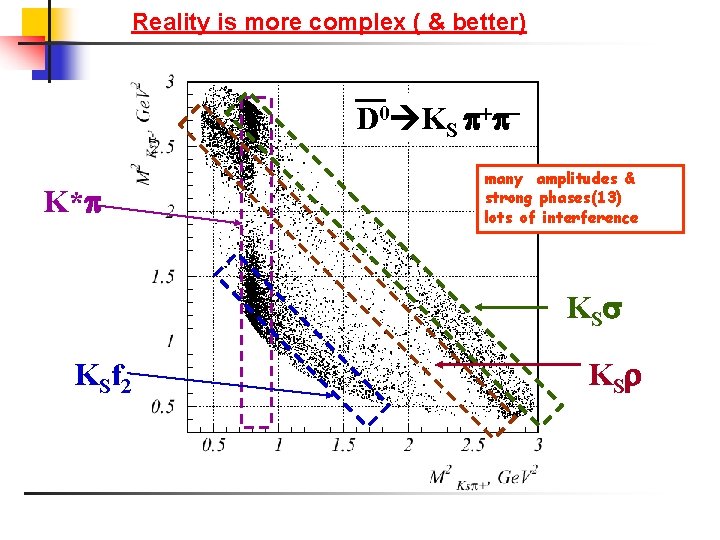
Reality is more complex ( & better) D 0 KS K* many amplitudes & strong phases(13) lots of interference K S f 2 K S
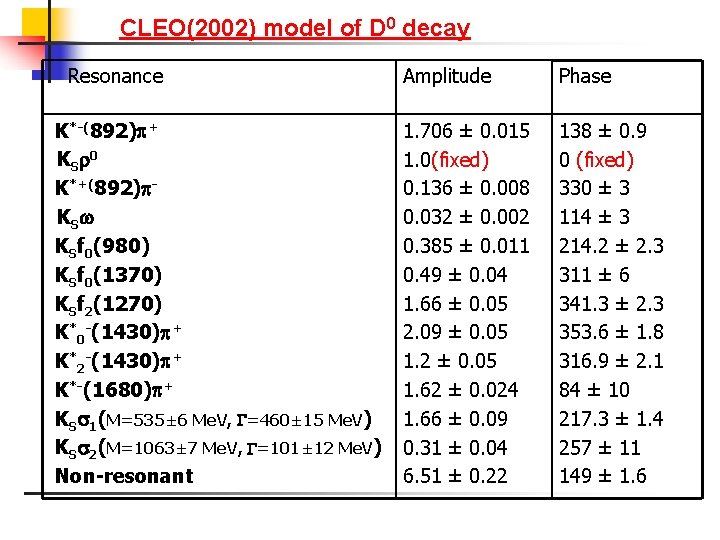
CLEO(2002) model of D 0 decay Resonance K*-(892) + KS 0 K*+(892) KS KSf 0(980) KSf 0(1370) KSf 2(1270) K*0 -(1430) + K*2 -(1430) + K*-(1680) + KS 1(M=535± 6 Me. V, =460± 15 Me. V) KS 2(M=1063± 7 Me. V, =101± 12 Me. V) Non-resonant Amplitude Phase 1. 706 ± 0. 015 1. 0(fixed) 0. 136 ± 0. 008 0. 032 ± 0. 002 0. 385 ± 0. 011 0. 49 ± 0. 04 1. 66 ± 0. 05 2. 09 ± 0. 05 1. 2 ± 0. 05 1. 62 ± 0. 024 1. 66 ± 0. 09 0. 31 ± 0. 04 6. 51 ± 0. 22 138 ± 0. 9 0 (fixed) 330 ± 3 114 ± 3 214. 2 ± 2. 3 311 ± 6 341. 3 ± 2. 3 353. 6 ± 1. 8 316. 9 ± 2. 1 84 ± 10 217. 3 ± 1. 4 257 ± 11 149 ± 1. 6
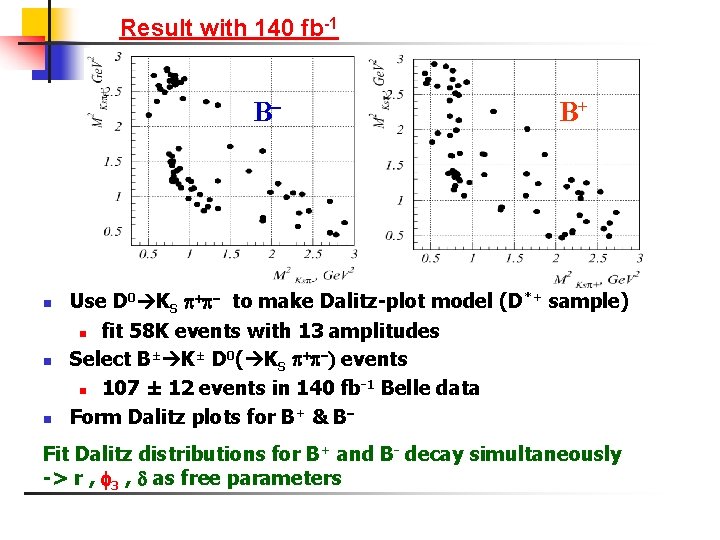
Result with 140 fb-1 B- n n n B+ Use D 0 KS - to make Dalitz-plot model (D*+ sample) n fit 58 K events with 13 amplitudes Select B± K± D 0( KS -) events -1 Belle data n 107 ± 12 events in 140 fb Form Dalitz plots for B+ & B- Fit Dalitz distributions for B+ and B- decay simultaneously -> r , 3 , as free parameters
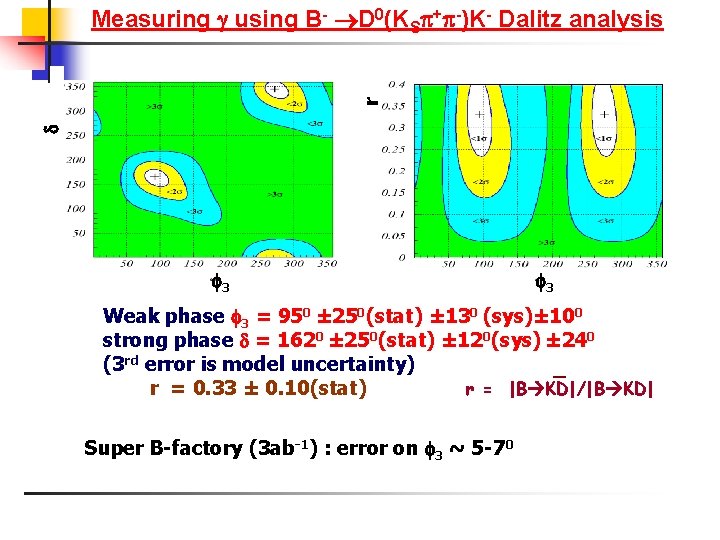
r Measuring using B- D 0(KS + -)K- Dalitz analysis 3 3 Weak phase 3 = 950 ± 250(stat) ± 130 (sys)± 100 strong phase = 1620 ± 250(stat) ± 120(sys) ± 240 (3 rd error is model uncertainty) _ r = |B KD|/|B KD| r = 0. 33 ± 0. 10(stat) Super B-factory (3 ab-1) : error on 3 ~ 5 -70
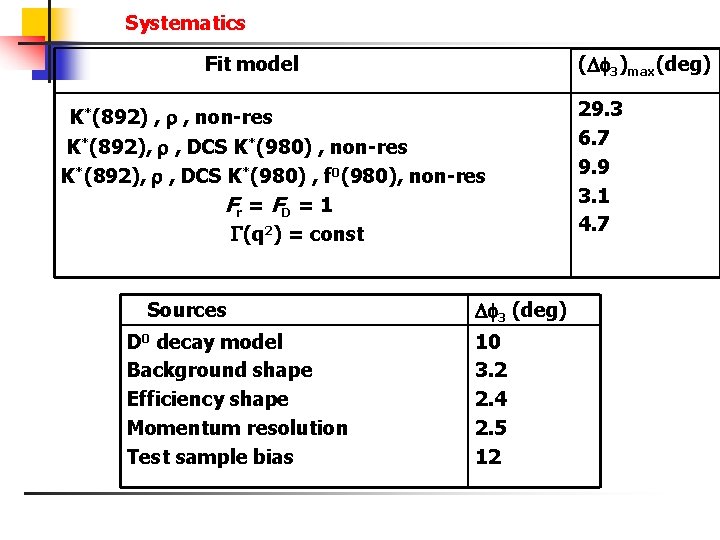
Systematics ( 3)max(deg) Fit model K*(892) , , non-res K*(892), , DCS K*(980) , f 0(980), non-res Fr = FD = 1 (q 2) = const Sources D 0 decay model Background shape Efficiency shape Momentum resolution Test sample bias 3 (deg) 10 3. 2 2. 4 2. 5 12 29. 3 6. 7 9. 9 3. 1 4. 7
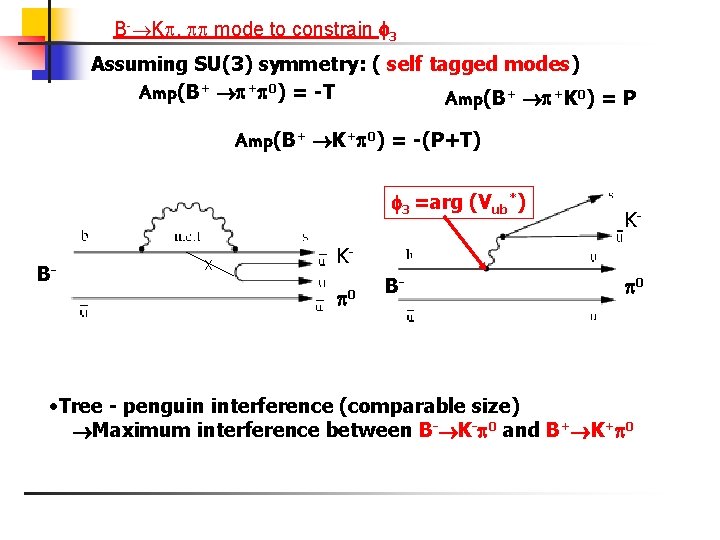
B- K , mode to constrain 3 Assuming SU(3) symmetry: ( self tagged modes) Amp(B+ + 0) = -T Amp(B+ +K 0) = P Amp(B+ K+ 0) = -(P+T) 3 =arg (Vub*) B- X K- K 0 B- 0 • Tree - penguin interference (comparable size) Maximum interference between B- K- 0 and B+ K+ 0
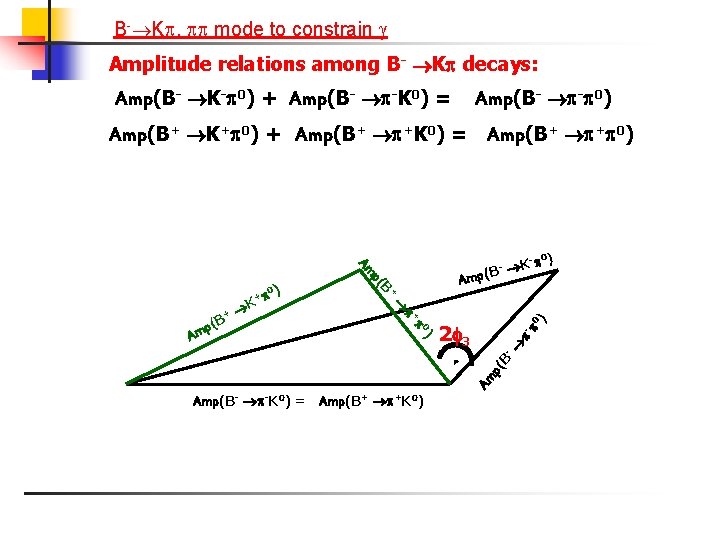
B- K , mode to constrain Amplitude relations among B- K decays: Amp(B- K- 0) + Amp(B- -K 0) = Amp(B- - 0) Amp(B+ K+ 0) + Amp(B+ +K 0) = Amp(B+ + 0) 0 ) Am p( B- ) 2 3 0 + (B + p Am K B + p( Am 0) + - 0) K B ( Amp - Amp(B- -K 0) = Amp(B+ +K 0)

CP asymmetry in K : 7% error @80 fb-1 1% error @3 ab-1 The error will be dominated by theory in Super-B factory Need better understanding HELP (TO THEORISTS) !
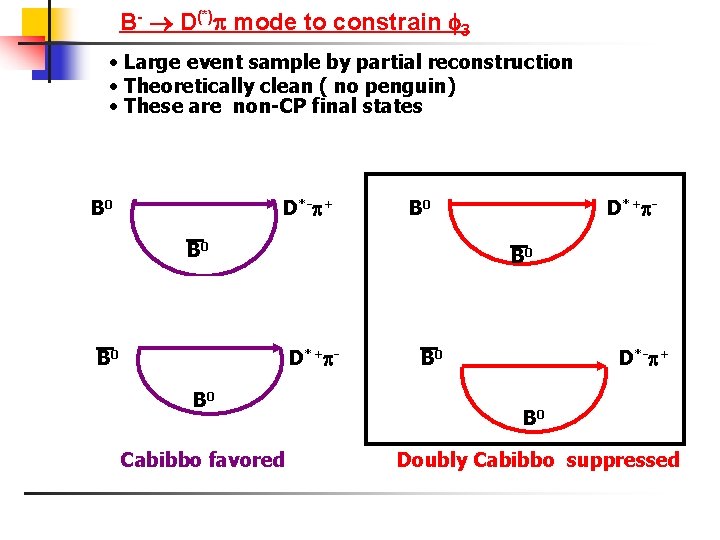
B- D(*) mode to constrain 3 • Large event sample by partial reconstruction • Theoretically clean ( no penguin) • These are non-CP final states D*- + B 0 B 0 D*+ - B 0 Cabibbo favored D*+ - B 0 D*- + B 0 Doubly Cabibbo suppressed
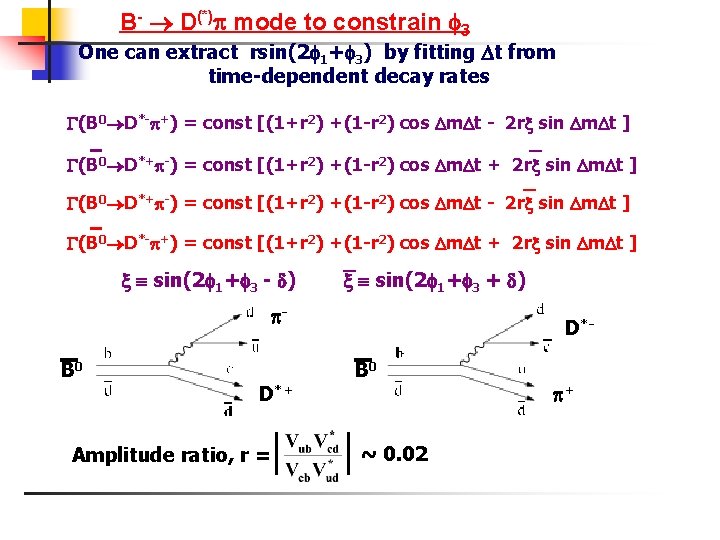
B- D(*) mode to constrain 3 One can extract rsin(2 1+ 3) by fitting t from time-dependent decay rates (B 0 D*- +) = const [(1+r 2) +(1 -r 2) cos m t - 2 r sin m t ] _ (B 0 D*+ -) = const [(1+r 2) +(1 -r 2) cos m t + 2 r sin m t ] _ (B 0 D*+ -) = const [(1+r 2) +(1 -r 2) cos m t - 2 r sin m t ] (B 0 D*- +) = const [(1+r 2) +(1 -r 2) cos m t + 2 r sin m t ] sin(2 1+ 3 - ) _ sin(2 1+ 3 + ) B 0 D*+ Amplitude ratio, r = D*B 0 ~ 0. 02 +
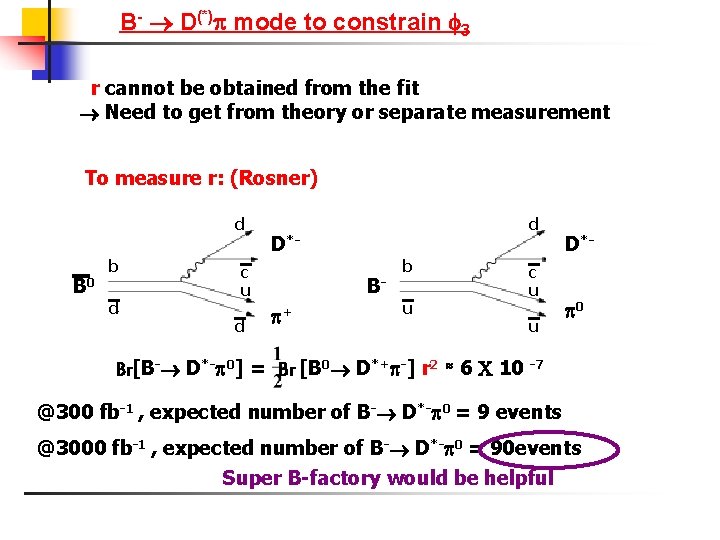
B- D(*) mode to constrain 3 r cannot be obtained from the fit Need to get from theory or separate measurement To measure r: (Rosner) d B 0 b d D*- c u d d B + b c u u Br[B- D*- 0] = Br [B 0 D*+ -] r 2 u D* 0 6 10 -7 @300 fb-1 , expected number of B- D*- 0 = 9 events @3000 fb-1 , expected number of B- D*- 0 = 90 events Super B-factory would be helpful
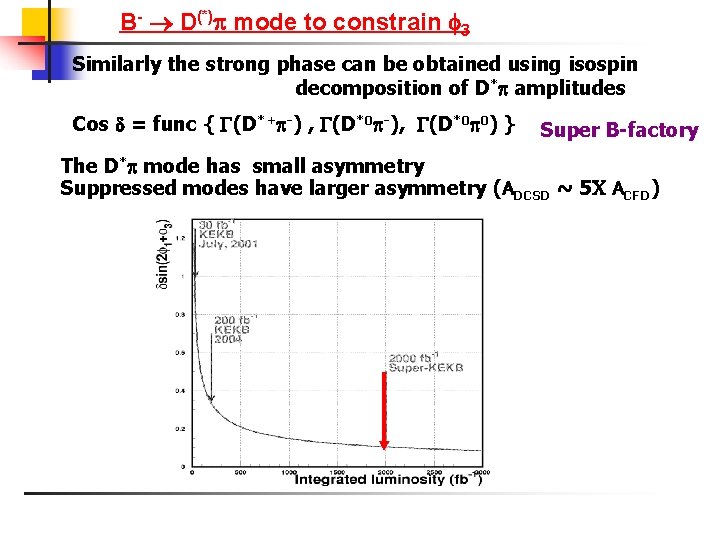
B- D(*) mode to constrain 3 Similarly the strong phase can be obtained using isospin decomposition of D* amplitudes Cos = func { (D*+ -) , (D*0 -), (D*0 0) } Super B-factory The D* mode has small asymmetry Suppressed modes have larger asymmetry (ADCSD ~ 5 ACFD)

Summary • There are many methods to constrain 3 We discussed: • B- DCPK(*)- needs value of “r” as input. r 2 = 0. 31 ± 0. 21 (assuming r =0. 2 r 2 = 0. 04, r 2 = ? ) • B- Ddcsd. K- is promising but need lots and lots of data • B K / has large theory uncertainty • B D* has a small asymmetry, need to measure “r” decay modes with large asymmetry have small BF’s decay modes with large BF’s have small asymmetry • Either way, one needs large data sample to constrain SUPER B-FACTORY IS NEEDED
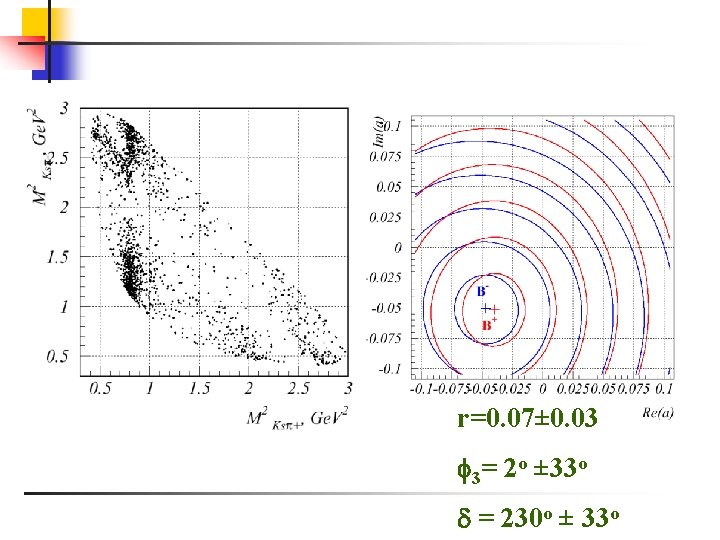
r=0. 07± 0. 03 3= 2 o ± 33 o = 230 o ± 33 o
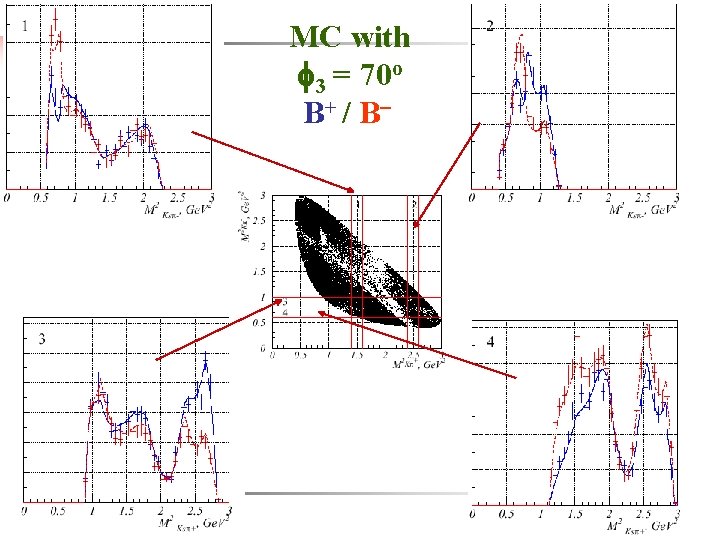
MC with 3 = 70 o B+ / B-
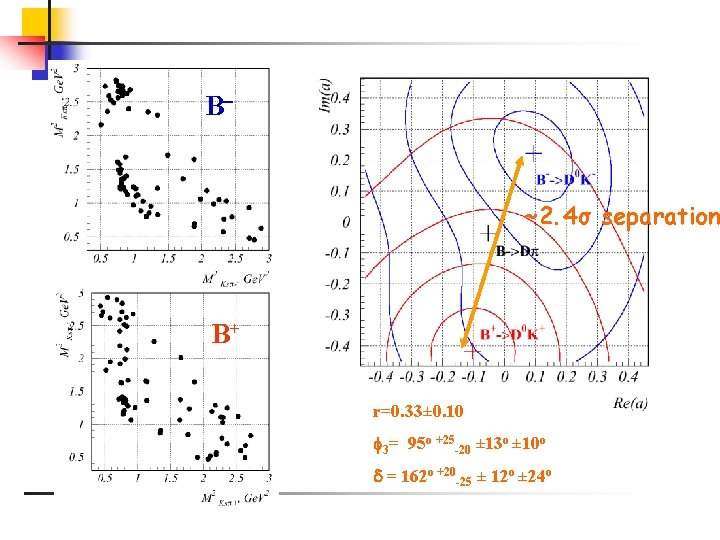
B- ~2. 4σ separation B+ r=0. 33± 0. 10 3= 95 o +25 -20 ± 13 o ± 10 o = 162 o +20 -25 ± 12 o ± 24 o
- Slides: 40