Measures of variation Dispersion According to Bow leys

Measures of variation Dispersion: According to “Bow leys” the dispersion is the measures of variation of the data items from the arithmetic mean. Consider the following three set of values having same average. total mean X 10 10 10 50 10 Y 12 14 8 6 10 50 10 z 28 3 4 10 5 50 10

Measures of variation or dispersion • Dispersion refers to the variation in the size of different values or the degree of scatteredness of the values of the variable. • Some others words or terms used in place of dispersion are spread, scatter, variability, and variation. In table given below two type of data given. In above both series mean =25 How can we check which data is more disperse? X 23 24 24 25 25 26 26 27 y 2 6 15 22 25 25 25 30 40 60

Some important measures of (variation)dispersion are as follow • Range • Deviation(mean deviation) • Standard deviation • variance • Coefficient of variance Note: Standard deviation and variance is used in finance to find out risk of loss or failure in the market in an investment.

Deviation The difference between a number in a data set and mean of the data set is called deviation. The deviation shows how much a number varies from mean. Sum of deviation always zero ∑(xi - µ)= 0
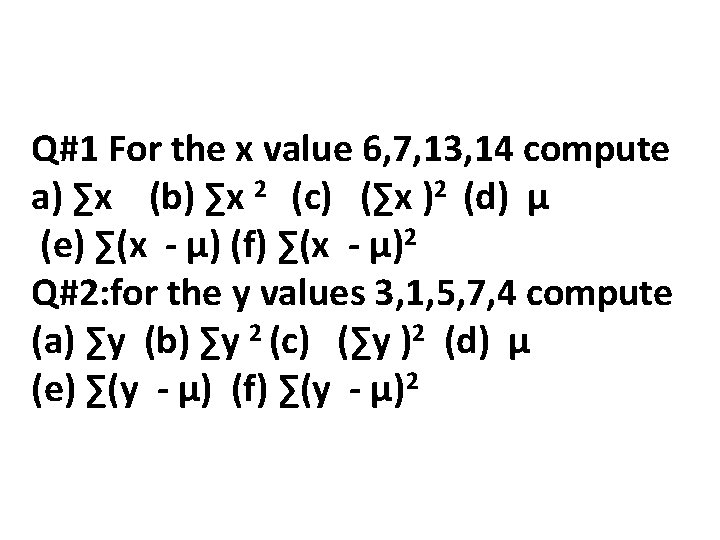
Q#1 For the x value 6, 7, 13, 14 compute a) ∑x (b) ∑x 2 (c) (∑x )2 (d) µ (e) ∑(x - µ) (f) ∑(x - µ)2 Q#2: for the y values 3, 1, 5, 7, 4 compute (a) ∑y (b) ∑y 2 (c) (∑y )2 (d) µ (e) ∑(y - µ) (f) ∑(y - µ)2

Q#3: for the data in table compute x y (a) ∑ x. y 1 17 (b) (∑x). (∑y) (c) ∑(x - µx). (y - µy) 4 6 9 12 2 2 (d) ∑x. y 11 6 5 13 15 9

Q#4: for the following data compute (a) ∑x (b) ∑(x - 4) (c) ∑y (d) ∑(y - 4) x 4 2 9 y 11 5 8

Standard deviation • The arithmetic mean and the variability measure called standard deviation. • Variance : Square of standard deviation is called variance. OR The square root of variance is called standard deviation.


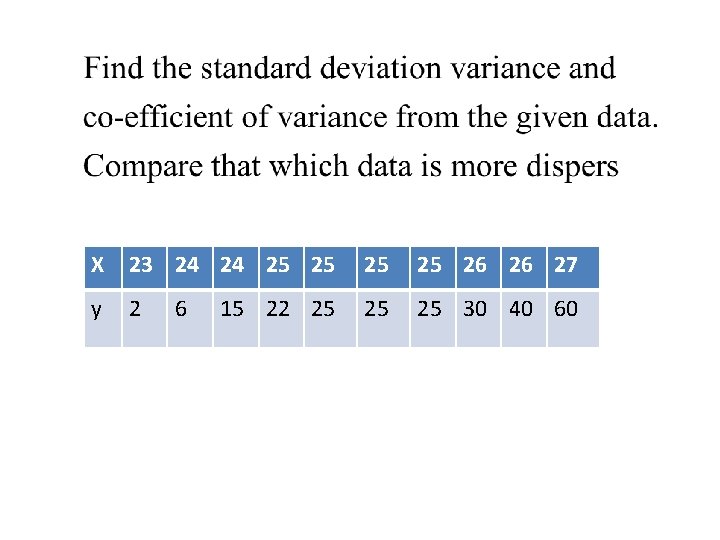
X 23 24 24 25 25 26 26 27 y 2 25 25 30 40 60 6 15 22 25
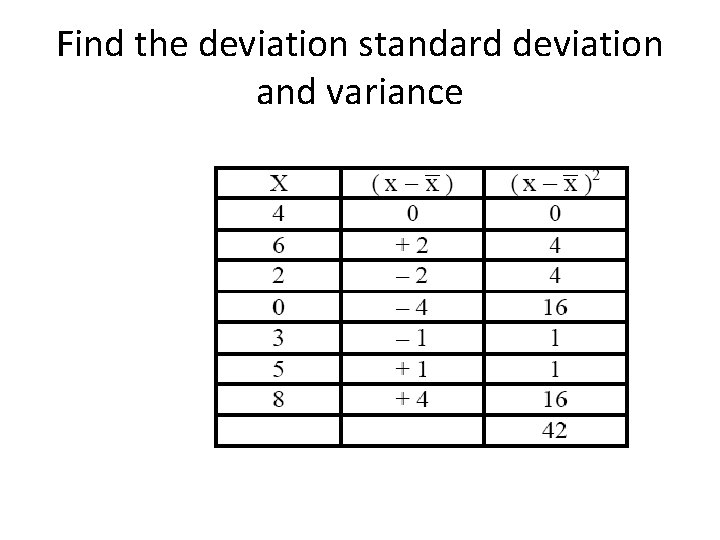
Find the deviation standard deviation and variance

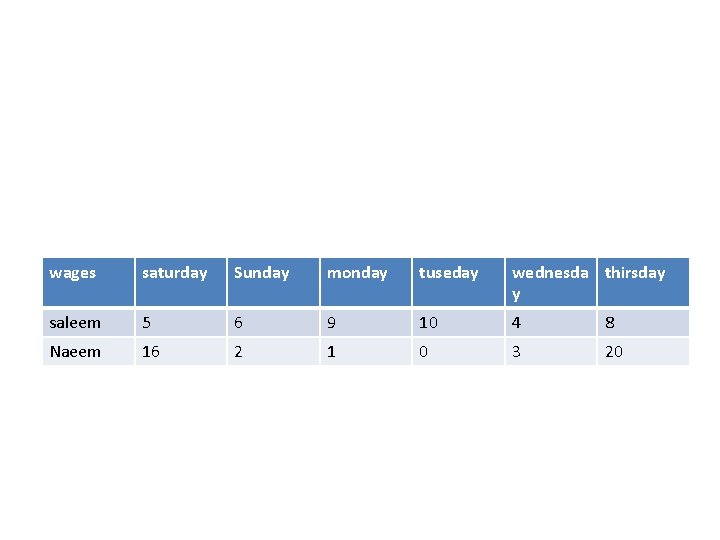
wages saturday Sunday monday tuseday wednesda thirsday y saleem 5 6 9 10 4 8 Naeem 16 2 1 0 3 20

Standard deviation and variance from ungrouped data

Standard deviation and variance from ungrouped data
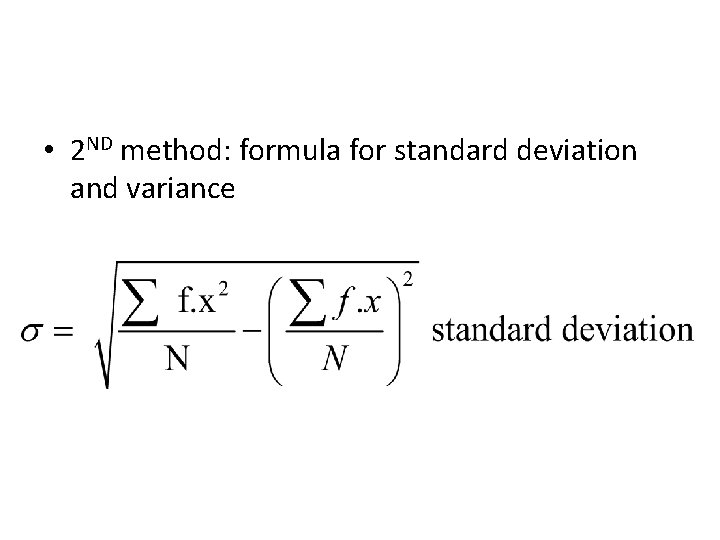
• 2 ND method: formula for standard deviation and variance
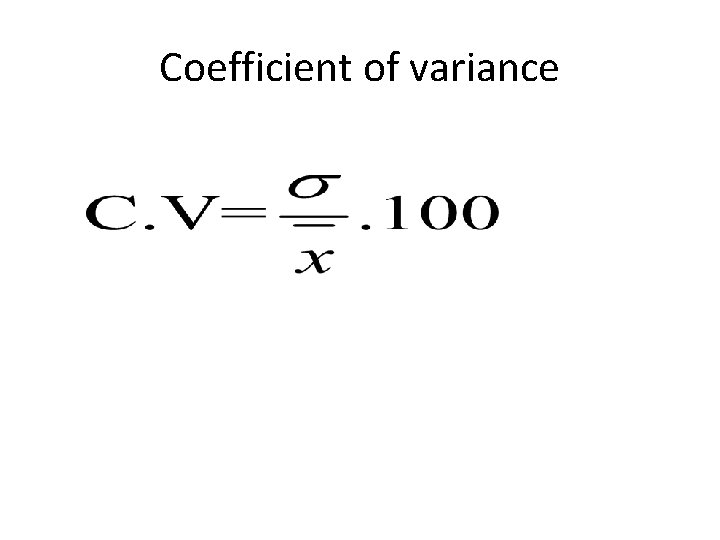
Coefficient of variance

Q: The number of runs scored by a player A and B during a test series of 5 test matches is shown below for each of of 10 innings: A 5 26 97 76 112 80 6 108 24 16 B 51 47 36 60 58 39 44 42 73 50 • Which of the player has shown more consistency?
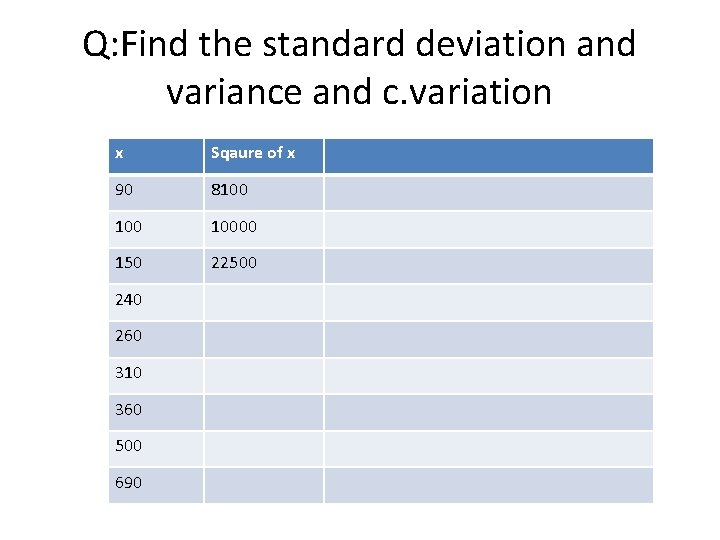
Q: Find the standard deviation and variance and c. variation x Sqaure of x 90 8100 10000 150 22500 240 260 310 360 500 690
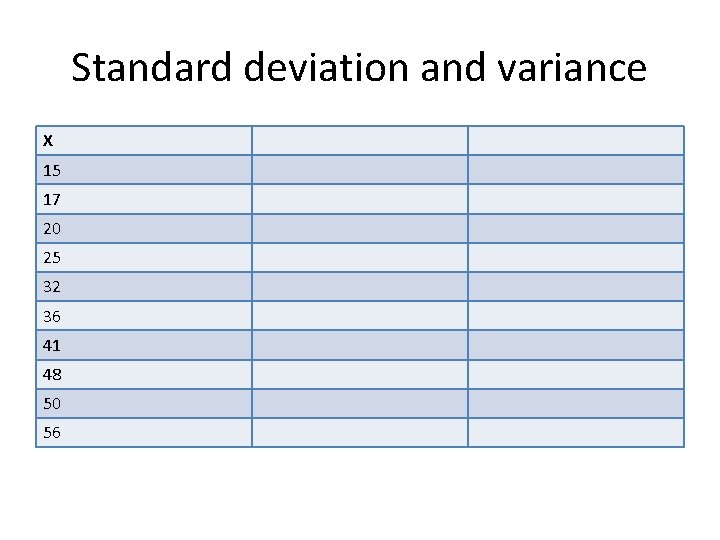
Standard deviation and variance X 15 17 20 25 32 36 41 48 50 56

Find the standard deviation and variance X 12 14 16 18 20 22 F 1 4 6 10 7 2 x 4 6 10 13 14 17 f 2 4 3 5 3 2

Find the standard deviation and variance from the given data X 30 31 32 33 34 35 36 37 38 39 F 4 8 23 35 62 44 18 4 1 1
- Slides: 23