Measures of Variation A measure of variation or

Measures of Variation A measure of variation or a measure of dispersion concerns the spread of the data about the mean. We will be finding measures of variation as well as interpreting those values.

Data Set Think of the one person you have texted the most since you woke up this morning. Count how many texts you have sent them. Record data on separate sheet.

How many texts were sent this morning? Minimum value: Maximum value:

Basic Concepts of Variation Range: the difference between the maximum data value and the minimum data value. Using today’s data set, find the range.

Variance of a Sample and a Population Variance: a measure of variation equal to the square of the standard deviation Sample variance: s 2 Square of the standard deviation s Population variance: σ2 Square of the population standard deviation σ

Basic Concepts of Variation Standard Deviation of a sample: a measure of variation of values about the mean s read “sample standard deviation” or σ read “population standard deviation” The “standard” measure of variation in the study of Statistics.

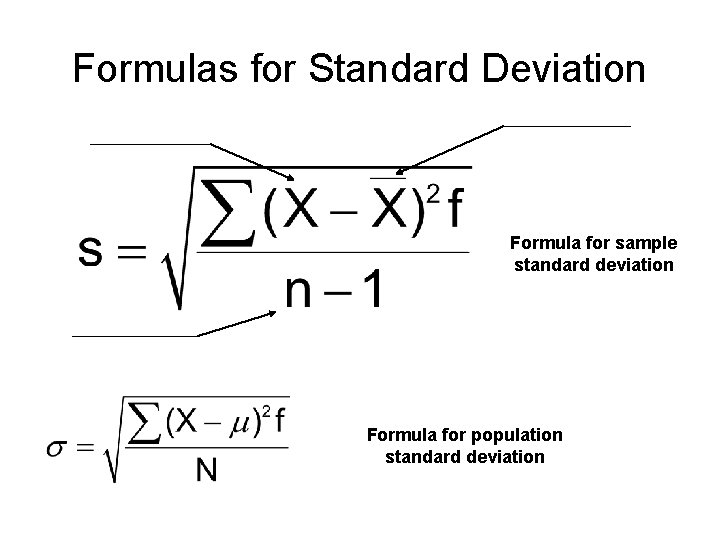
Formulas for Standard Deviation Formula for sample standard deviation Formula for population standard deviation

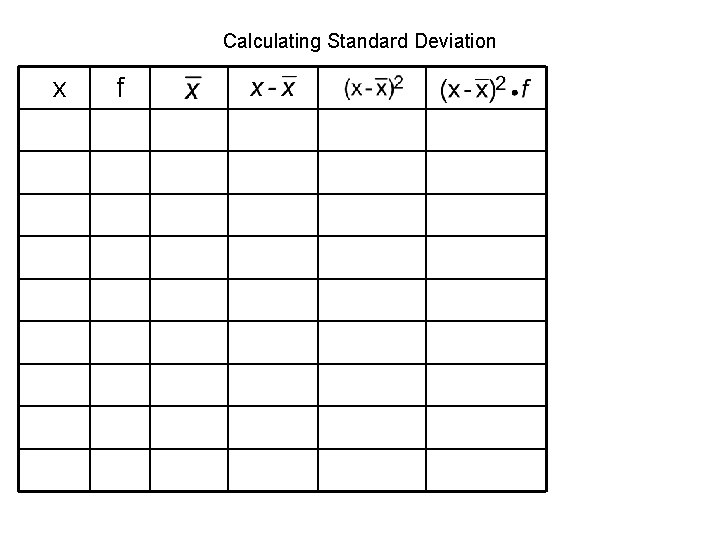
Calculating Standard Deviation x f

Steps to finding standard deviation 1. Compute the mean 2. Subtract the mean from each individual sample value. The result is a list of deviations of the form 3. Square each of the deviations obtained from step 2. This produces numbers of the form 4. Add all of the squares obtained from step 3. The result is 5. Divide the total from step 4 by the number n – 1, which is 1 less than the total number of sample values. 6. Find the square root of the result of step 5. The result is the standard deviation.

Steps to finding standard deviation on calculator • • Enter data into a list Double check your list!! Go to STAT Over to CALC Menu Choose 1. 1 -Var Stats Use appropriate list and hit Enter or Calculate “Sx” = sample standard deviation *NOTE* To calculate Sample Variance, Square the Sample Standard Deviation

Interpreting known Standard Deviation Values Usual values in a data set are those typical and not too extreme. If the standard deviation of a data set is known, use it to estimate the minimum and maximum usual sample values. Minimum “usual” value = (mean) – 2 x (standard deviation) Maximum “usual” value = mean + 2 x (standard deviation)

Heights of Men Previous results from the National Health Survey show that heights of men have a mean of 69. 0 inches and a standard deviation of 2. 8 in. Find the minimum and maximum “usual” heights. a) Daniel Tosh’s height is 6’ 3’’. Is his height unusual? b) How about “Wee-Man” who is 4’ 6’’? Is he unusually short?

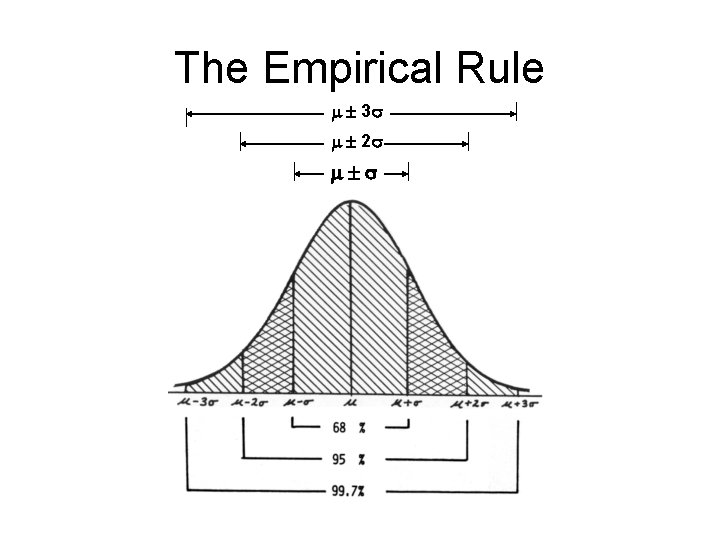
Interpreting Known Standard Deviation Values Empirical (or 68 -95 -99. 7) Rule for Data: Properties for data with an approximate bellshaped distribution are: • About 68% of all values fall within 1 standard deviation of the mean. • About 95% of all values fall within 2 standard deviations of the mean. • About 99. 7 of all values fall within 3 standard deviations of the mean.

The Empirical Rule 3 2

Chebyshev’s Theorem Cheby’s Theorem works for ANY distribution and gives rough estimates for values that are more than one standard deviation above or below the mean. • At least 75% of all values lie within 2 standard deviations of the mean. • At least 89% of all values lie within 3 standard deviations of the mean. • At least 94% of all values lie within 4 standard deviations of the mean

CLASS EXAMPLES: 1. Heights of Men have a bell-shaped distribution and have a mean of 69 in and a standard deviation of 2. 8 in. Using the empirical rule, a) What percentage of men have heights between 60. 6 in and 77. 4 in? b) What percentage of men have heights between 66. 2 in and 71. 8 in? c) What percentage of men have heights between 63. 4 in and 74. 6 in? 2. Cholesterol levels of men have a mean of 178. 1 and a standard deviation of 40. 7. Using Cheby’s Theorem, a) What percentage of men have cholesterol levels between 56 and 300. 2? b) What percentage of men have cholesterol levels between 15. 3 and 340. 9? c) What percentage of men have cholesterol levels between 96. 7 and 259. 5?

How Chebyshev’s Theorem differs from the Empirical Rule • Chebyshev’s Theorem applies to any data set without restriction. • The Empirical Rule applies to data sets with an approximately bell-shaped distribution. • Chebyshev’s Theorem is more general and provides a rougher estimate than the more specific Empirical Rule.

Objective: How do we measure position? Basic Concepts: 1. 2. 3. 4. z scores Percentiles Quartiles Boxplots

z Scores z score (or standardized value): the number of standard deviations a given data value lies above or below the mean for samples for population **Round off rule for z scores to two decimal places**

Classwork Example Comparing Heights Former NBA star Michael Jordan is 78 in. tall, and WNBA basketball player Rebecca Lobo is 76 in. tall. Jordan is obviously taller than Lobo by 2 in. , but which player is relatively taller? Does Jordan’s height among men exceed Lobo’s height among women? Men have heights with a mean of 69. 0 in. and a standard deviation of 2. 8 in. ; women have heights with a mean of 63. 6 in. and a standard deviation of 2. 5 in. (based on data from the National Health Survey). To compare the heights of Jordan and Lobo relative to the populations of men and women, we need to standardize these heights.

Recall: To find a given data value when you have a z-score use the following formula: *Note* Positive z-score has a value above the mean. Negative z-score has a value below the mean. A z-score of zero has the value that is the mean.

Classwork Example Quiz grades have a mean of 78 and a standard deviation of 8. You have been informed that you scored one and a half standard deviations above the mean. YAY! But, what did you get on the test? You know your z-score BUT you don’t know your raw score. You need to “unstandardize” What if you heard your friend scored 2 standard deviations below the mean, what did he get?

Percentiles Quantiles: evenly partitioning sorted data values into percentiles, quartiles, and deciles with approximately equal numbers of data values Percentiles: There are 99 percentiles; P 1, P 2, … , P 99, which partition the data into 100 groups with about 1% of the data values in each group. Deciles: There are 9 deciles; D 1, D 2, … , D 9, which partition the data into 10 groups with about 10% of the data values in each group. Quartiles: There are 3 quartiles; Q 1, Q 2, and Q 3 which partition the data into 4 groups with about 25% of the data values in each group. Q 1 = P 25 Q 2 = P 50 Q 3 = P 75

How to compute a percentile for a given data value 1. Data values must be ordered (sorted). 2. Use the formula: 3. Round to the nearest whole number

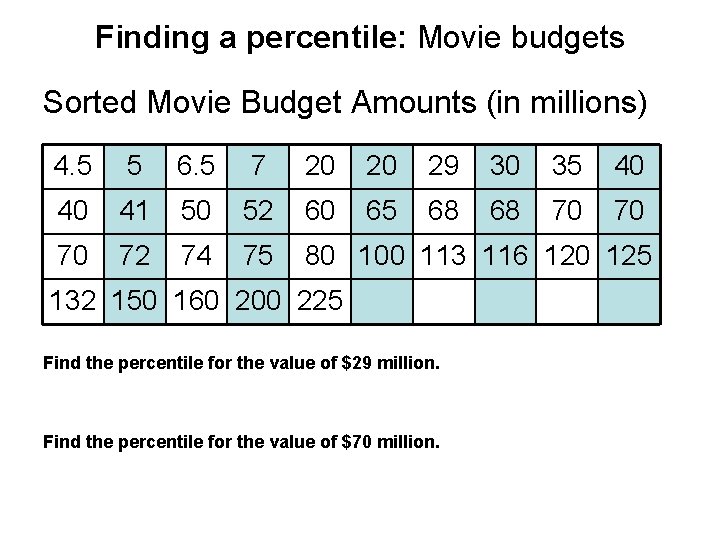
Finding a percentile: Movie budgets Sorted Movie Budget Amounts (in millions) 4. 5 5 6. 5 7 20 20 29 30 35 40 40 41 50 52 60 65 68 68 70 70 70 72 74 75 80 100 113 116 120 125 132 150 160 200 225 Find the percentile for the value of $29 million. Find the percentile for the value of $70 million.

How to compute a data value for a given percentile 1. Data values must be ordered (sorted). 2. Use the formula: 3. If L is a whole number: then use that location! If L is a not a whole number: Choose the next higher data value. k= n= L= Pk =

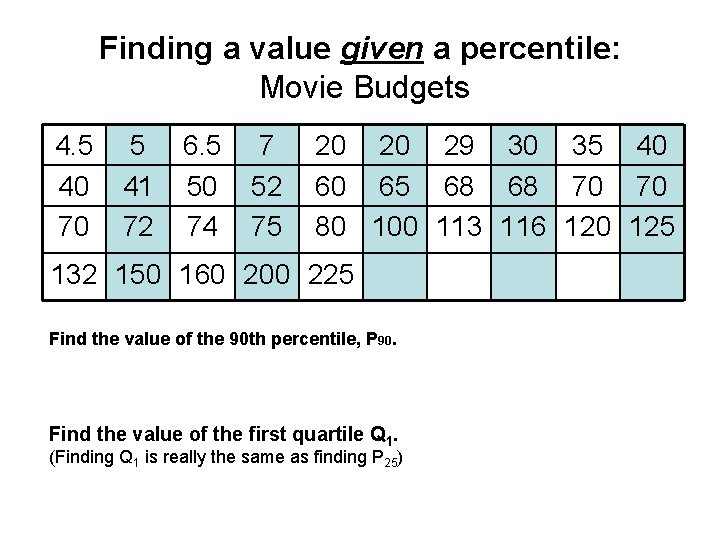
Finding a value given a percentile: Movie Budgets 4. 5 40 70 5 41 72 6. 5 50 74 7 52 75 20 20 29 30 35 40 60 65 68 68 70 70 80 100 113 116 120 125 132 150 160 200 225 Find the value of the 90 th percentile, P 90. Find the value of the first quartile Q 1. (Finding Q 1 is really the same as finding P 25)

Outliers Outlier: a data value that is located very far away from almost all of the other data values. – an outlier can have a dramatic effect on the mean, – an outlier can have a dramatic effect on the standard deviation, – an outlier can have a dramatic effect on the scale of the histogram.

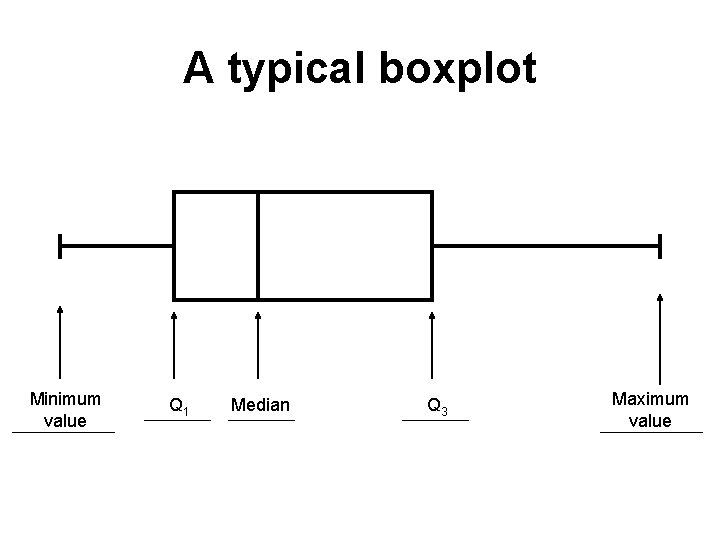
Boxplots 5 -Number Summary: For a set of data, the minimum data value, Q 1, the median, Q 3, and the maximum data value. Boxplot (or box-and-whisker diagram): a graph which contains a line which extends from the minimum data value to the maximum data value and a box with lines drawn at Q 1, the median, and Q 3. Modified Boxplot is a boxplot that displays outliers!!!!

A typical boxplot Minimum value Q 1 Median Q 3 Maximum value