Measures of Variability Ungrouped Data There are six

Measures of Variability Ungrouped Data

There are six measures of variability: 1. Range 2. Mean Average Deviation 3. Interquartile Range 4. Quartile Deviation 5. Variance 6. Standard Deviation

The Range Honestly, it is the most basic of all. You just have to get the difference between the largest number and the smallest number.

Example 1 I am thinking of 10 random numbers: 69, 21, 37, 82, 49, 48, 27, 24, 111, 35. What is my range? 90

Example 2 Now I have another set of numbers: 48, 20, 37, 27, 15, 26, 52 What is my range? 37

Mean Absolute Deviation • It is the average distance between each data value and the mean.

How to solve MAD? Find out the mean For each number, subtract the mean Take the absolute value Work out the average of those.

Example 1 Five random scores in a 50 -item test were taken: 37, 49, 25, 29, 50 Mean = 38

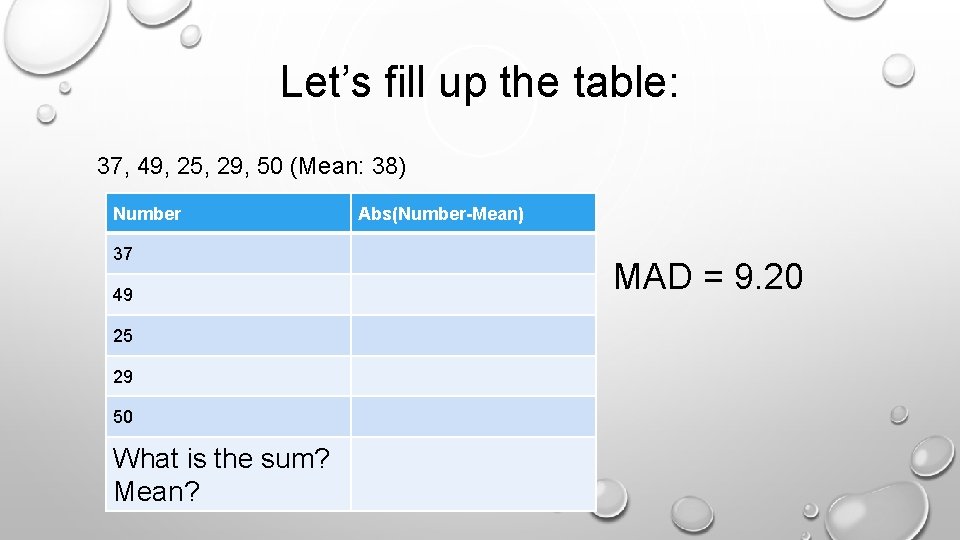
Let’s fill up the table: 37, 49, 25, 29, 50 (Mean: 38) Number 37 49 25 29 50 What is the sum? Mean? Abs(Number-Mean) MAD = 9. 20

Huh? Prove it! The table should look like this: (Mean: 38) Number Abs(Number-Mean) 37 1 49 11 25 13 29 9 50 12 Sum=46 46/5=9. 20 MAD = 9. 20

Example 2 Six bakers were tasked to make as many cookies as they can within an hour: 162, 201, 134, 177, 184, 150 Mean = 168

Let’s fill up the table: 162, 201, 134, 177, 182, 150 (Mean: 168) Number Abs(Number-Mean) 162 201 134 177 182 150 What is the sum? Mean? MAD = 19. 00

How to do this? The table should look like this: (Mean: 168) Number Abs(Number-Mean) 162 6 201 33 134 34 177 9 182 14 150 18 Sum=114 114/6=19 MAD = 19. 00

Quartile Deviation • Basically, it is half the interquartile range.

The Interquartile Range • It is one of the most popular measures of variation. • It is the difference of the third quartile and the first quartile.

Example 1 12 students took a 30 -item test, and here were the results: 17, 28, 9, 15, 20, 3, 20, 15, 22, 29, 17, 30 First, sort them in order: 3, 9, 15, 17, 20, 22, 28, 29, 30

Solution 3, 9, 15, 17, 20, 22, 28, 29, 30 3. 75 th 15 9. 25 th 23. 50 -15 8. 50 Quartile Deviation = 4. 25

Example 2 15 students measured their height, and here were the results (cm): 148, 137, 155, 150, 160, 146, 155, 157, 148, 140, 150, 162, 157, 147, 161 First, sort them in order: 137, 140, 146, 147, 148, 150, 155, 157, 160, 161, 162

Solution 137, 140, 146, 147, 148, 150, 155, 157, 160, 161, 162 4. 50 th 147. 50 11. 50 th 157. 00 -147. 50 9. 50 cm Quartile Deviation = 4. 75 cm

Standard Deviation • It measures the spread of the data about the mean value. • Also useful in comparing sets of data that have the same mean but different range.

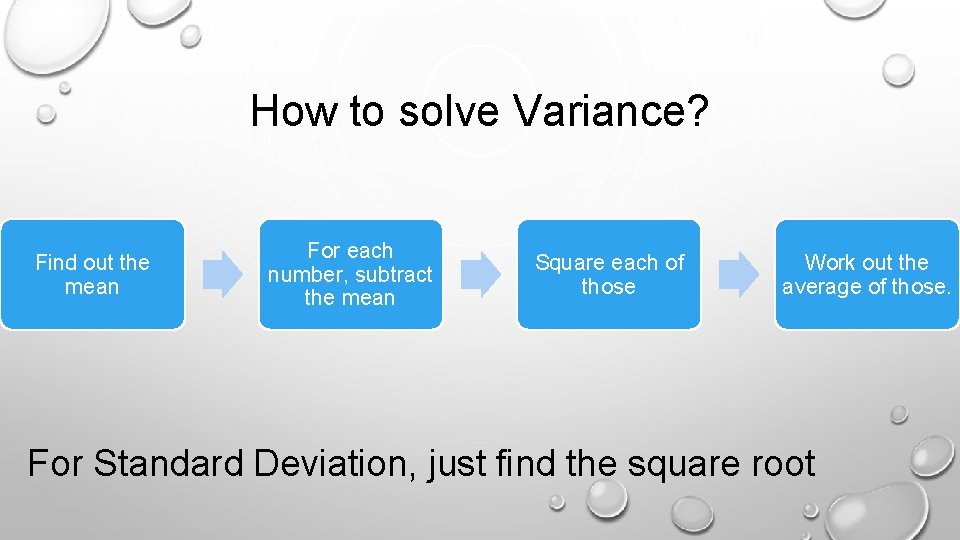
How to solve Variance? Find out the mean For each number, subtract the mean Square each of those Work out the average of those. For Standard Deviation, just find the square root

Example 1 Six random scores in a 100 -item test were taken: 30, 82, 57, 37, 52, 66 Mean = 54

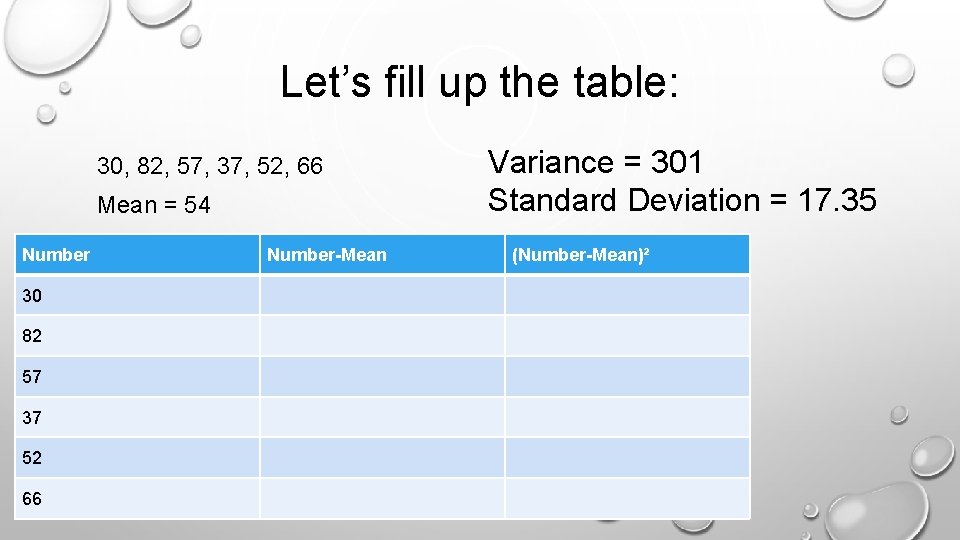
Let’s fill up the table: 30, 82, 57, 37, 52, 66 Mean = 54 Number 30 82 57 37 52 66 Number-Mean Variance = 301 Standard Deviation = 17. 35 (Number-Mean)²

How do you do it? The table should look like this: 30, 82, 57, 37, 52, 66 (Mean: 54) Number-Mean (Number-Mean)² 30 -24 576 82 28 784 57 3 9 37 -17 289 52 -2 4 66 12 144 Variance = 301 Standard Deviation = 17. 35 Sum=1, 806/6=301 Square root of 301 is 17. 35

Example 2 In a week, here were the number of shirts sold in a store: 17, 40, 26, 66, 91, 104, 55 Mean = 57

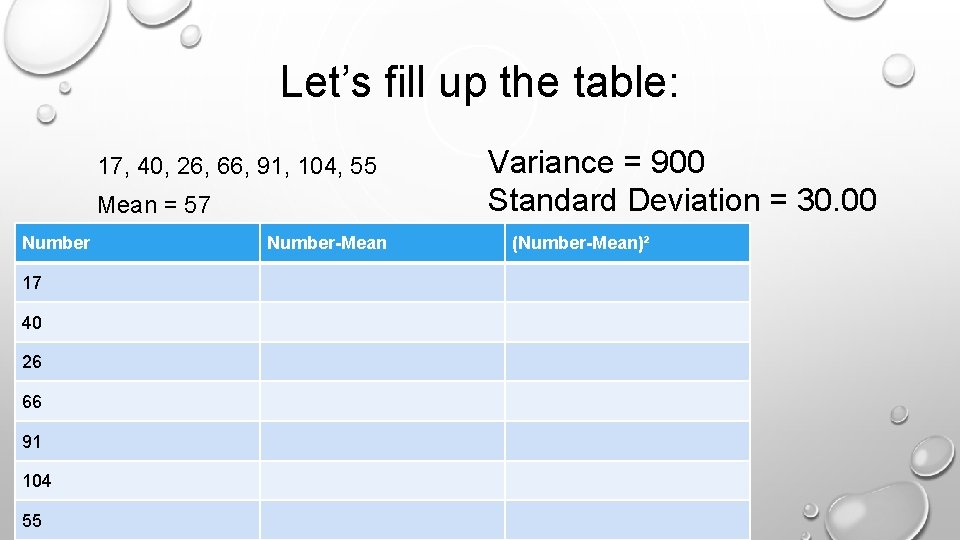
Let’s fill up the table: 17, 40, 26, 66, 91, 104, 55 Mean = 57 Number 17 40 26 66 91 104 55 Number-Mean Variance = 900 Standard Deviation = 30. 00 (Number-Mean)²

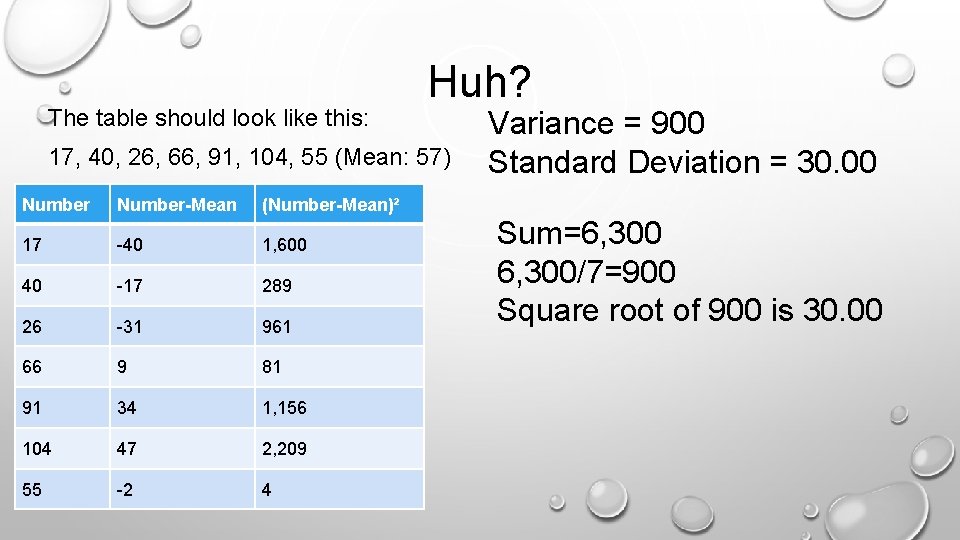
The table should look like this: Huh? 17, 40, 26, 66, 91, 104, 55 (Mean: 57) Number-Mean (Number-Mean)² 17 -40 1, 600 40 -17 289 26 -31 961 66 9 81 91 34 1, 156 104 47 2, 209 55 -2 4 Variance = 900 Standard Deviation = 30. 00 Sum=6, 300/7=900 Square root of 900 is 30. 00

Assigned task! When going home tonight, kindly check out the following website: http: //bit. ly/assignedtask 3 point 4