Measures of Variability Descriptive Statistics Part 2 Cal

Measures of Variability Descriptive Statistics Part 2 Cal State Northridge 320 Andrew Ainsworth Ph. D

Reducing Distributions p. Regardless of numbers of scores, distributions can be described with three pieces of info: n Shape (Normal, Skewed, etc. ) n Central Tendency n Variability Psy 320 - Cal State Northridge 2

How do scores spread out? p. Variability n. Tell us how far scores spread out n. Tells us how the degree to which scores deviate from the central tendency Psy 320 - Cal State Northridge 3

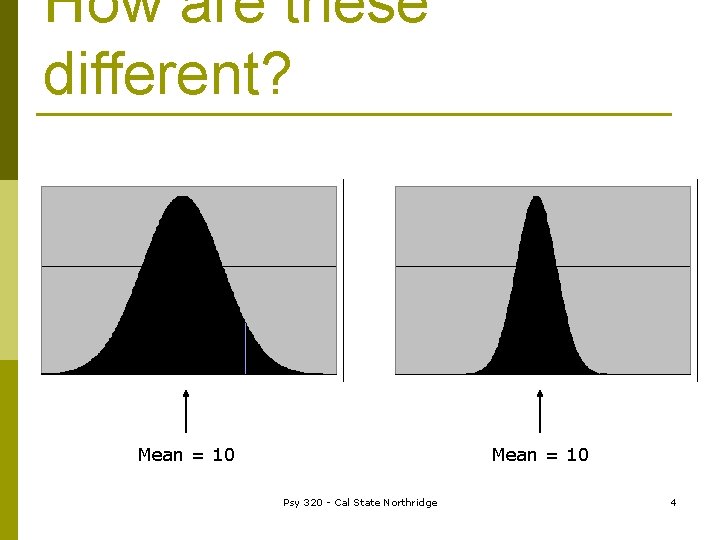
How are these different? Mean = 10 Psy 320 - Cal State Northridge 4

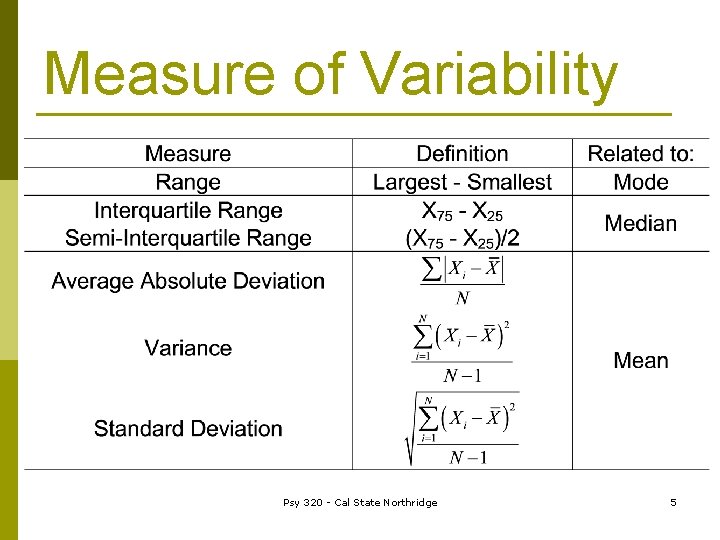
Measure of Variability Psy 320 - Cal State Northridge 5

The Range p The simplest measure of variability n Range (R) = Xhighest – Xlowest n Advantage – Easy to Calculate n Disadvantages p Like Median, only dependent on two scores unstable {0, 8, 9, 9, 11, 53} Range = 53 {0, 8, 9, 9, 11} Range = 11 p Does not reflect all scores 6

Detour: Percentile p A percentile is the score at which a specified percentage of scores in a distribution fall below n p To say a score 53 is in the 75 th percentile is to say that 75% of all scores are less than 53 The percentile rank of a score indicates the percentage of scores in the distribution that fall at or below that score. n Thus, for example, to say that the percentile rank of 53 is 75, is to say that 75% of the scores on the exam are less than 53. Psy 320 - Cal State Northridge 7

Detour: Percentile p Scores which divide distributions into specific proportions n Percentiles = hundredths P 1, P 2, P 3, … P 97, P 98, P 99 n Quartiles = quarters Q 1, Q 2, Q 3 n Deciles = tenths D 1, D 2, D 3, D 4, D 5, D 6, D 7, D 8, D 9 p Percentiles are the SCORES Psy 320 - Cal State Northridge 8

Detour: Percentile Ranks p What percent of the scores fall below a particular score? p Percentile Ranks are the Ranks not the scores Psy 320 - Cal State Northridge 9

Detour: Percentile Rank p Ranking no ties p Ranking to ties with ties – just number them - assign midpoint Psy 320 - Cal State Northridge 10

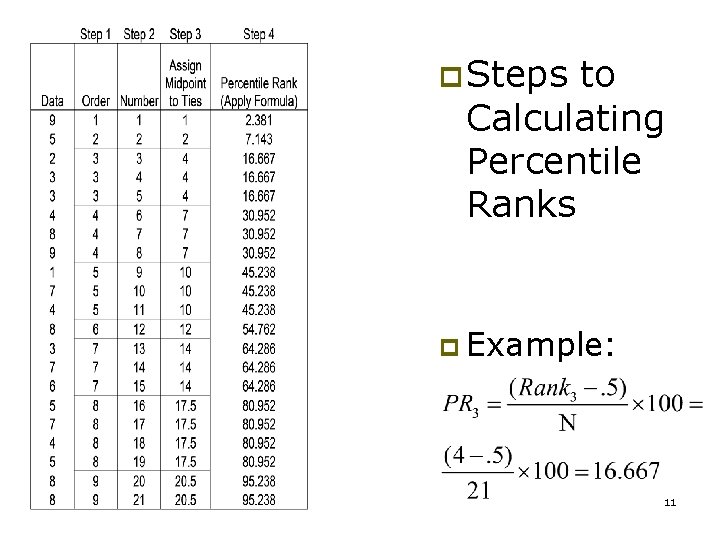
p Steps to Calculating Percentile Ranks p Example: 11

Detour: Finding a Percentile in a Distribution Where XP is the score at the desired percentile, p is the desired percentile (a number between 0 and 1) and n is the number of scores) p If the number is an integer, than the desired percentile is that number p If the number is not an integer than you can either round or interpolate p 12

Detour: Interpolation Method Steps p Apply the formula 1. 2. 3. 4. 5. You’ll get a number like 7. 5 (think of it as place 1. proportion) Start with the value indicated by place 1 (e. g. 7. 5, start with the value in the 7 th place) Find place 2 which is the next highest place number (e. g. the 8 th place) and subtract the value in place 1 from the value in place 2, this distance 1 Multiple the proportion number by the distance 1 value, this is distance 2 Add distance 2 to the value in place 1 and that 13 is the interpolated value

Detour: Finding a Percentile in a Distribution p Interpolation Method Example: p 25 th percentile: {1, 4, 9, 16, 25, 36, 49, 64, 81} p X 25 = (. 25)(9+1) = 2. 5 n place 1 = 2, proportion =. 5 n Value in place 1 = 4 n Value in place 2 = 9 n distance 1 = 9 – 4 = 5 n distance 2 = 5 *. 5 = 2. 5 n Interpolated value = 4 + 2. 5 = 6. 5 n 6. 5 is the 25 th percentile 14

Detour: Finding a Percentile in a Distribution p Interpolation Method Example 2: p 75 th percentile {1, 4, 9, 16, 25, 36, 49, 64, 81} p X 75 = (. 75)(9+1) = 7. 5 n place 1 = 7, proportion =. 5 n Value in place 1 = 49 n Value in place 2 = 64 n distance 1 = 64 – 49 = 15 n distance 2 = 15 *. 5 = 7. 5 n Interpolated value = 49 + 7. 5 = 56. 5 n 56. 5 is the 75 th percentile 15

Detour: Rounding Method Steps p Apply 1. 2. 3. the formula You’ll get a number like 7. 5 (think of it as place 1. proportion) If the proportion value is any value other than exactly. 5 round normally If the proportion value is exactly. 5 p p And the p value you’re looking for is above. 5 round down (e. g. if p is. 75 and Xp = 7. 5 round down to 7) And the p value you’re looking for is below. 5 round up (e. g. if p is. 25 and Xp = 2. 5 round up to 3) Psy 320 - Cal State Northridge 16

Detour: Finding a Percentile in a Distribution p Rounding Method Example: p 25 th percentile {1, 4, 9, 16, 25, 36, 49, 64, 81} p X 25 = (. 25)(9+1) = 2. 5 (which becomes 3 after rounding up), p The 3 rd score is 9, so 9 is the 25 th percentile Psy 320 - Cal State Northridge 17

Detour: Finding a Percentile in a Distribution p Rounding Method Example 2: p 75 th percentile {1, 4, 9, 16, 25, 36, 49, 64, 81} p X 75 = (. 75)(9+1) = 7. 5 which becomes 7 after rounding down p The 7 th score is 49 so 49 is the 75 th percentile Psy 320 - Cal State Northridge 18

Detour: Quartiles p To calculate Quartiles you simply find the scores the correspond to the 25, 50 and 75 percentiles. p Q 1 = P 25, Q 2 = P 50, Q 3 = P 75 Psy 320 - Cal State Northridge 19

Back to Variability: IQR p Interquartile Range n= P 75 – P 25 or Q 3 – Q 1 n This helps to get a range that is not influenced by the extreme high and low scores n Where the range is the spread across 100% of the scores, the IQR is the spread across the middle 50% Psy 320 - Cal State Northridge 20

Variability: SIQR p Semi-interquartile n =(P 75 range – P 25)/2 or (Q 3 – Q 1)/2 n IQR/2 n This is the spread of the middle 25% of the data n The average distance of Q 1 and Q 3 from the median n Better for skewed data Psy 320 - Cal State Northridge 21

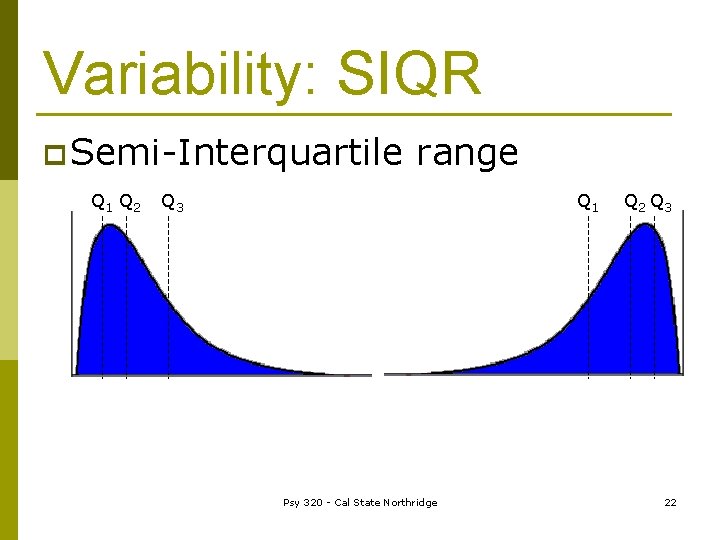
Variability: SIQR p Semi-Interquartile Q 1 Q 2 range Q 3 Q 1 Psy 320 - Cal State Northridge Q 2 Q 3 22

Average Absolute Deviation p Average distance of all scores from the mean disregarding direction. Psy 320 - Cal State Northridge 23

Average Absolute Deviation Psy 320 - Cal State Northridge 24

Average Absolute Deviation p Advantages Uses all scores n Calculations based on a measure of central tendency - the mean. n p Disadvantages Uses absolute values, disregards direction n Discards information n p Cannot be used for further calculations Psy 320 - Cal State Northridge 25

Variance p The average squared distance of each score from the mean p Also known as the mean square p Variance of a sample: s 2 p Variance of a population: s 2 Psy 320 - Cal State Northridge 26

Variance p When calculated for a sample p When calculated for the entire population Psy 320 - Cal State Northridge 27

Variance p Variance Example n Data set = {8, 6, 4, 2} n Step 1: Find the Mean Psy 320 - Cal State Northridge 28

Variance p Variance Example n Data set = {8, 6, 4, 2} n Step 2: Subtract mean from each value 29

Variance p Variance Example n Data set = {8, 6, 4, 2} n Step 3: Square each deviation 30

Variance p Variance Example n Data set = {8, 6, 4, 2} n Step 4: Add the squared deviations and divide by N - 1 31

Standard Deviation p Variance is in squared units p What about regular old units p Standard Deviation = Square root of the variance Psy 320 - Cal State Northridge 32

Standard Deviation p Uses measure of central tendency (i. e. mean) p Uses all data points p Has a special relationship with the normal curve (we’ll see this soon) p Can be used in further calculations p Standard Deviation of Sample = SD or s p Standard Deviation of Population = Psy 320 - Cal State Northridge 33

Why N-1? p When using a sample (which we always do) we want a statistic that is the best estimate of the parameter Psy 320 - Cal State Northridge 34

Degrees of Freedom p Usually referred to as df p Number of observations minus the number of restrictions __+__+__+__=10 - 4 free spaces 2 +__+__+__=10 - 3 free spaces 2 + 4 +__+__=10 - 2 free spaces 2 + 4 + 3 +__=10 Last space is not free!! Only 3 dfs. Psy 320 - Cal State Northridge 35

Boxplots Psy 320 - Cal State Northridge 36

Boxplots with Outliers Psy 320 - Cal State Northridge 37

Computational Formulas p Algebraic Equivalents that are easier to calculate Psy 320 - Cal State Northridge 38