Measures of Regression Prediction Interval Variation About a

Measures of Regression Prediction Interval

Variation About a Regression Line • Three types of variation about a regression line • • • Total variation Explained variation Unexplained variation • To find these variations, you must first calculate • • • The total deviation The explained deviation The unexplained deviation For each ordered pair (xi, yi) in a data set. .

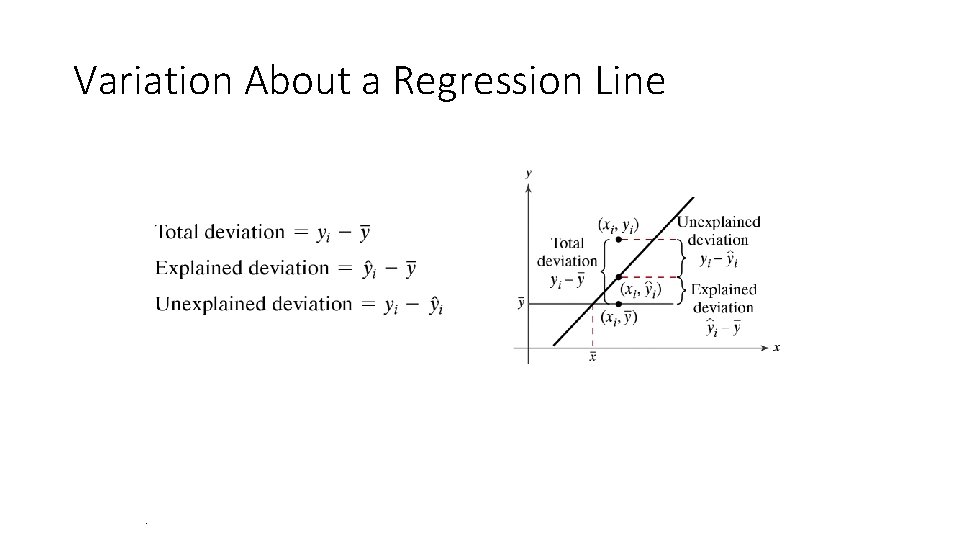
Variation About a Regression Line .

Variation About a Regression Line Total variation • The sum of the squares of the differences between the y-value of each ordered pair and the mean of y. Total variation = Explained variation • The sum of the squares of the differences between each predicted yvalue and the mean of y. Explained variation =.

Variation About a Regression Line Unexplained variation • The sum of the squares of the differences between the y-value of each ordered pair and each corresponding predicted y-value. Unexplained variation = The sum of the explained and unexplained variation is equal to the total variation. Total variation = Explained variation + Unexplained variation.

Coefficient of Determination Coefficient of determination • The ratio of the explained variation to the total variation. • Denoted by r 2 .

Example: Coefficient of Determination The correlation coefficient for the gross domestic products and carbon dioxide emissions data is r ≈ 0. 874. Find the coefficient of determination. What does this tell you about the explained variation of the data about the regression line? About the unexplained variation? About 76. 4% of the variation in the carbon emissions can be explained by the variation in the gross domestic products. About 23. 6% of the variation is unexplained. .

The Standard Error of Estimate Standard error of estimate • The standard deviation of the observed yi -values about the predicted ŷ-value for a given xi -value. It is given by n is the number of ordered pairs in the data set • The closer the observed y-values are to the predicted y-values, the smaller the standard error of estimate will be. .

The Standard Error of Estimate In Words 1. Make a table that includes the column heading shown. 2. Use the regression equation to calculate the predicted y-values. 3. Calculate the sum of the squares of the differences between each observed y-value and the corresponding predicted y-value. 4. Find the standard error of estimate. . In Symbols

Example: Standard Error of Estimate The regression equation for the gross domestic products and carbon dioxide emissions data is ŷ = 199. 535 x + 56. 036 Find the standard error of estimate. Solution: Use a table to calculate the sum of the squared differences of each observed y-value and the corresponding predicted y-value. .

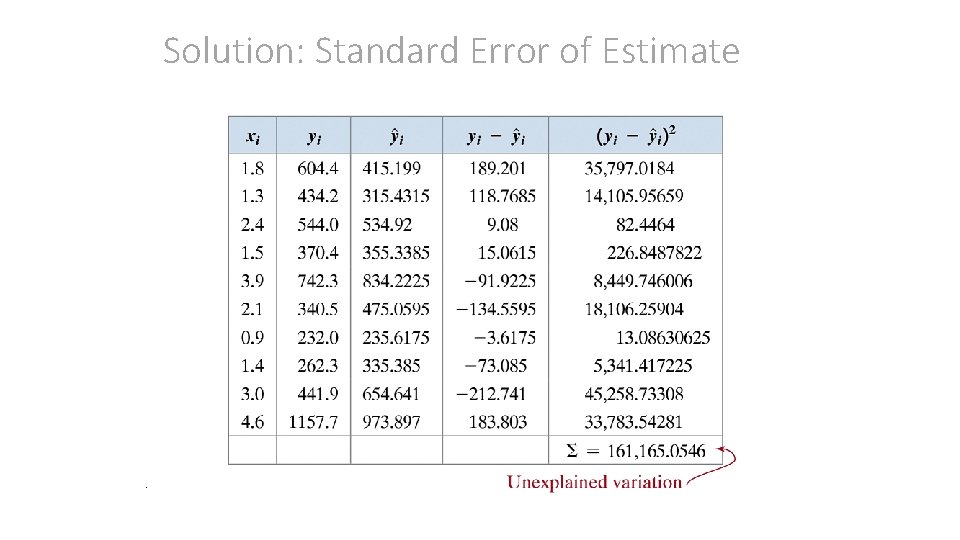
Solution: Standard Error of Estimate .

Solution: Standard Error of Estimate • n = 10, Σ(yi – ŷ i)2 = 161, 165. 0546 The standard error of estimate of the carbon dioxide emissions for a specific gross domestic product is about 141. 935 million metric tons. .

Prediction Intervals • Two variables have a bivariate normal distribution if for any fixed value of x, the corresponding values of y are normally distributed and for any fixed values of y, the corresponding x-values are normally distributed. .

Prediction Intervals • A prediction interval can be constructed for the true value of y. • Given a linear regression equation ŷ = mx + b and x 0, a specific value of x, a c-prediction interval for y is ŷ–E<y<ŷ +E where • The point estimate is ŷ and the margin of error is E. The probability that the prediction interval contains y is c, assuming that the estimation process is repeated a large number of times. .

Constructing a Prediction Interval for y for a Specific Value of x In Words 1. Identify the number of ordered pairs in the data set n and the degrees of freedom. In Symbols d. f. = n – 2 2. Use the regression equation and the given x-value to find the point estimate ŷ. 3. Find the critical value tc that corresponds to the given level of confidence c. . Use Table 5 in Appendix B.

Constructing a Prediction Interval for y for a Specific Value of x In Words In Symbols 4. Find the standard error of estimate se. 5. Find the margin of error E. 6. Find the left and right endpoints and form the prediction interval. . Left endpoint: ŷ – E Right endpoint: ŷ + E Interval: ŷ – E < y < ŷ + E

Example: Constructing a Prediction Interval Construct a 90% prediction interval for the carbon dioxide emission when the gross domestic product is $2. 8 trillion. What can you conclude? Solution: Because n = 10, there are d. f. = 10 – 2 = 8 degrees of freedom. .

Solution: Constructing a Prediction Interval • .

Solution: Constructing a Prediction Interval .

Solution: Constructing a Prediction Interval .