Measures of Central Tendency Measures of Central Tendency

Measures of Central Tendency

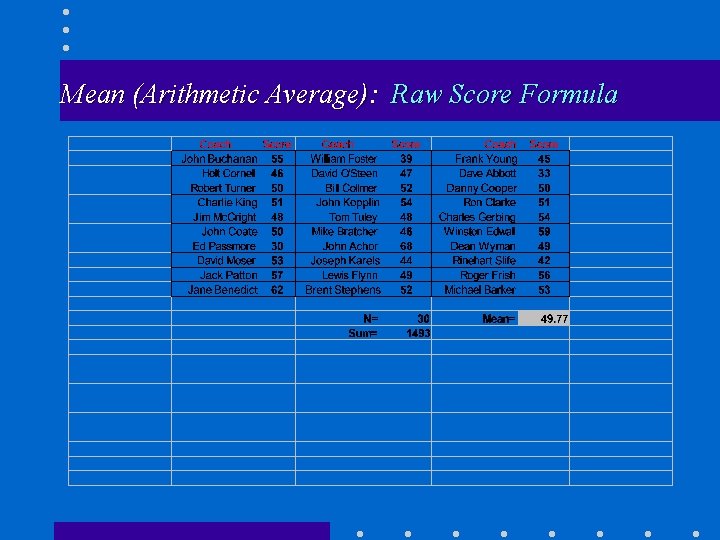
Measures of Central Tendency Mean (Arithmetic Average) Mean Computed from raw scores.

Mean (Arithmetic Average): Raw Score Formula

Measures of Central Tendency Mean (Arithmetic Average) Mean Computed from grouped scores. (A frequency Distribution) = 3408. 5 = 33 103. 29

Measures of Central Tendency Mean (Arithmetic Average) Mean Computed from Guessed Average

Measures of Central Tendency The Mean (Average) • Advantages – Most stable measure – Can perform algebraic operations – Basis for advanced statistics – Gives us the Center of Gravity of a dist. – Value depends on every score in dist. • Disadvantages – Weights extreme scores more than other measures of Central Tendency.

To Summarize: • Calculations for both grouped and ungrouped data. • Use raw scores when possible • Use grouped formula to calculate from freq. . . dist. or graph. Measures of Central Tendency • Guessed Average & Arbitrary Origin methods are seldom used today, but we need to be aware of them. • Raw score methods have the advantage of being more precise, because they use the exact value of every score in the distribution. • Next we will discuss - The Median

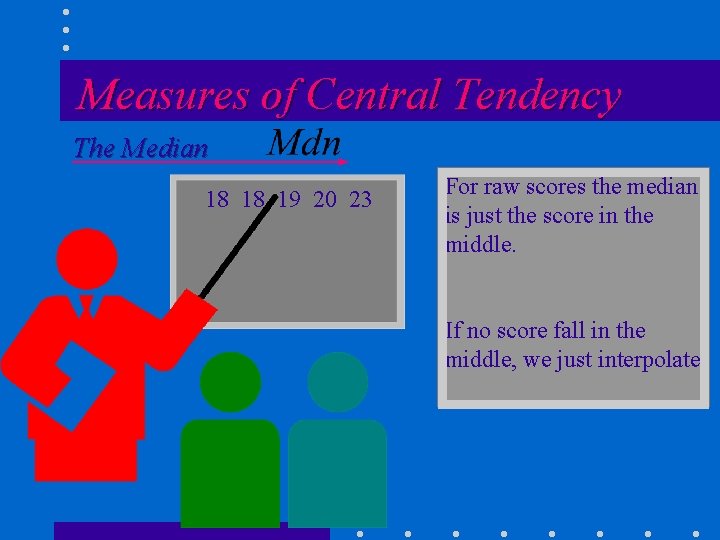
The Median

Measures of Central Tendency The Median The median is the point on the scale of measurement above which, and below which 50% of the scores are located.

Measures of Central Tendency The Median 18 18 19 20 23 For raw scores the median is just the score in the middle. If no score fall in the middle, we just interpolate.

Measures of Central Tendency The Median • Median Computed from Group Data -

Measures of Central Tendency The Median • Median Computed from Group Data - an e Th di e M

Measures of Central Tendency The Median. . . • Advantages – Easy to calculate. – Not influenced by extreme scores, so it can be used when we have extreme values. – The median divides the distribution into two equal groups. • Disadvantages – It is less stable than the mean. – The median will not permit all algebraic operations (addition & subtraction) because we usually have ordinal scales

The Mode

Measures of Central Tendency • The Mode – Ungrouped Data • The mode is the score which occurs most frequently. – Grouped Data • The mode is the midpoint of the class interval containing the largest number of cases. – Estimating the Mode from the Mean and Median • Mo = 3(Mdn)-2(Mean) • For use in skewed distributions. • Also distributions which are bimodal.

Measures of Central Tendency The Mode. . . • Advantages – Easy to calculate. – It is most appropriate for discreet Data. – It gives the most typical case. • Disadvantages – It is the least stable measure of central tendency. – Different size class intervals yield different results – If two non-adjacent class intervals have the same frequency, the distribution is bimodal and the mode is meaningless. • May suggest two distributions. – Can’t perform arithmetic or algebraic expressions with Mo.

Measures of Central Tendency Next: Measures of Variability