Measures of Central Tendency Arithmetic Mean Geometric Mean

Measures of Central Tendency Arithmetic Mean Geometric Mean Harmonic Mean

Meaning of Average An average is a value which can be taken as a representative of the whole distribution. “Average is a value which is typical or representative of a set of data” - Murray R. Spiegal

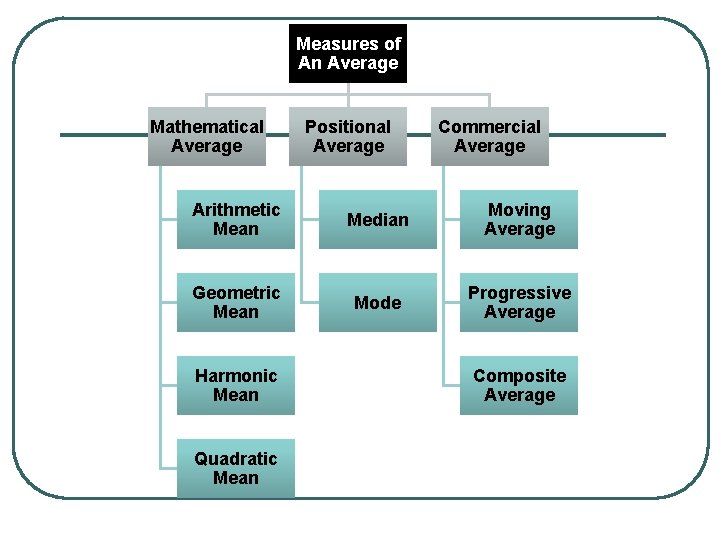
Measures of An Average Mathematical Average Positional Average Commercial Average Arithmetic Mean Median Moving Average Geometric Mean Mode Progressive Average Harmonic Mean Quadratic Mean Composite Average

Requisites of a Good Average Easy to Understand & Simple to compute Based on all the items Not be unduly affected by extreme observations Rigidly Defined Capable of further Algebraic Treatment Sampling Stability

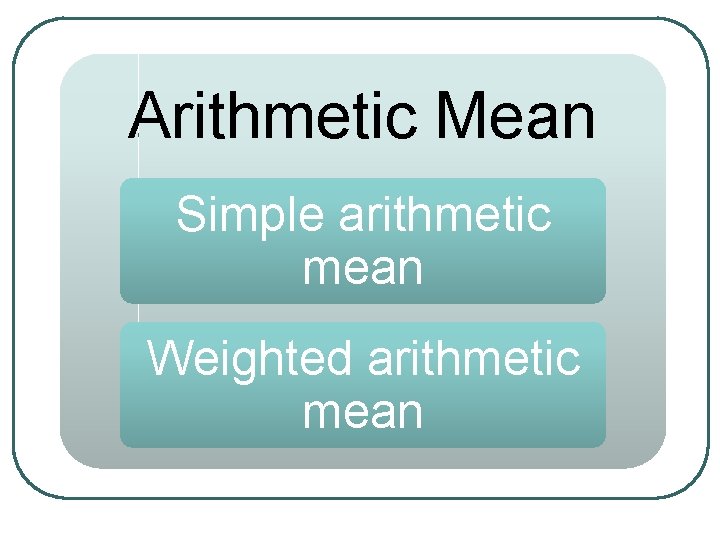
Arithmetic Mean Simple arithmetic mean Weighted arithmetic mean

Mathematical Properties of Arithmetic mean l l l The sum of deviations of the observations from the AM is always zero The sum of the squared deviations of the observations from AM is minimum AM is capable of being treated algebraically

Mathematical Properties of Arithmetic mean l

Mathematical Properties of Arithmetic mean l l If a constant B is added (subtracted) from every observation, the mean of these observations also gets added (subtracted) by it. If every observation is multiplied (divided) by a constant β, the mean of these observations also gets multiplied (divided) by it.

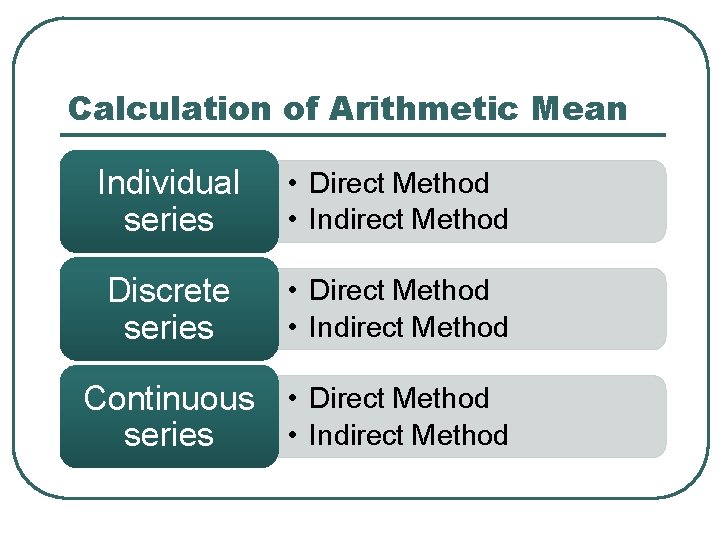
Calculation of Arithmetic Mean Individual series • Direct Method • Indirect Method Discrete series • Direct Method • Indirect Method Continuous • Direct Method • Indirect Method series

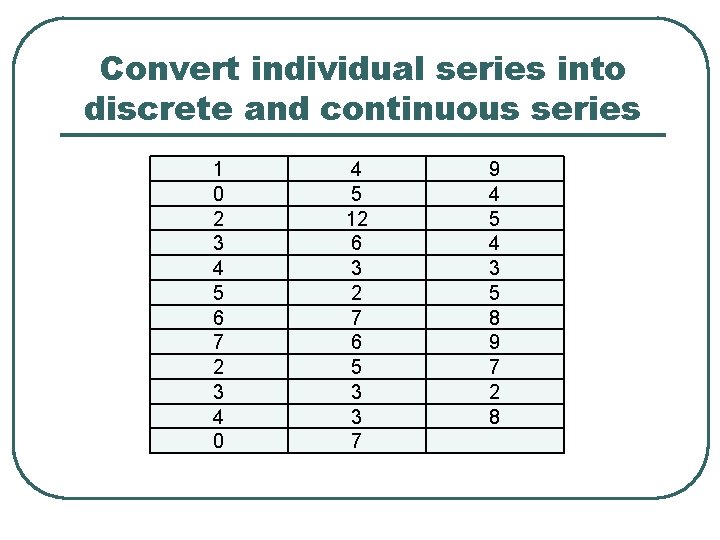
Convert individual series into discrete and continuous series 1 0 2 3 4 5 6 7 2 3 4 0 4 5 12 6 3 2 7 6 5 3 3 7 9 4 5 4 3 5 8 9 7 2 8

Calculate mean (Individual series) Monthly income of 10 employees in an office is given below. Calculate arithmetic mean of monthly income. Inco me (Rs. ) 1780 1760 1690 1750 1840 1920 1100 1810 1050 1950

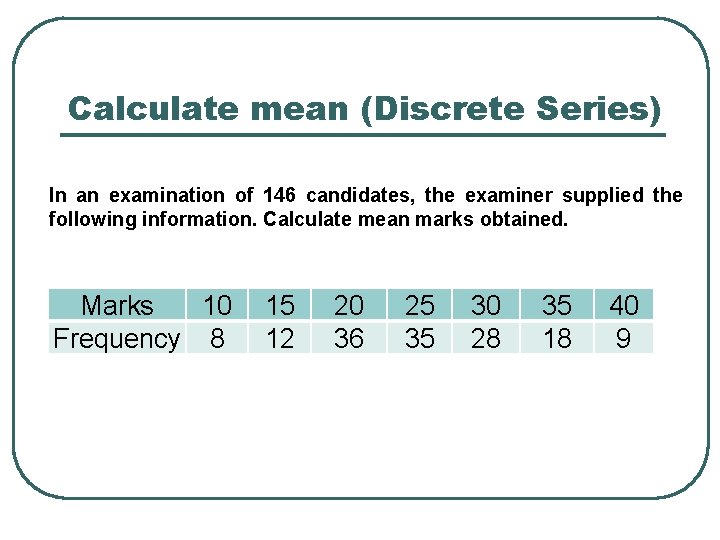
Calculate mean (Discrete Series) In an examination of 146 candidates, the examiner supplied the following information. Calculate mean marks obtained. Marks 10 Frequency 8 15 12 20 36 25 35 30 28 35 18 40 9

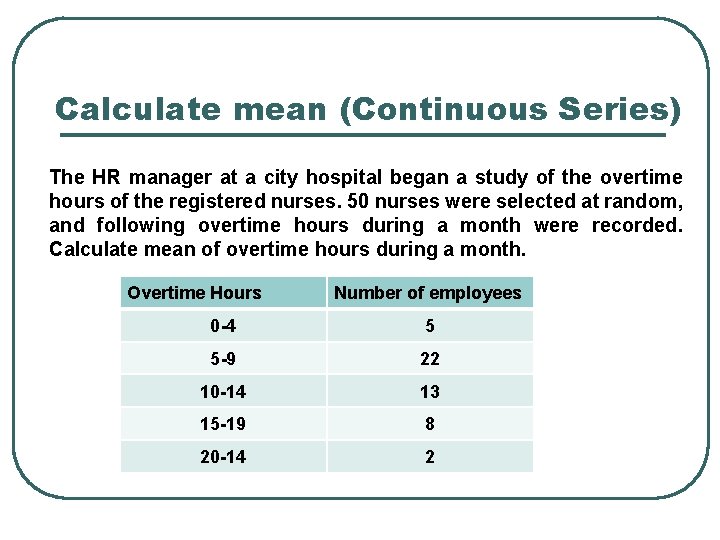
Calculate mean (Continuous Series) The HR manager at a city hospital began a study of the overtime hours of the registered nurses. 50 nurses were selected at random, and following overtime hours during a month were recorded. Calculate mean of overtime hours during a month. Overtime Hours Number of employees 0 -4 5 5 -9 22 10 -14 13 15 -19 8 20 -14 2

Some special types of problems

l l l Unequal class interval Inclusive series Open ended series More than or less than cumulative frequency Correcting incorrect value Combined mean

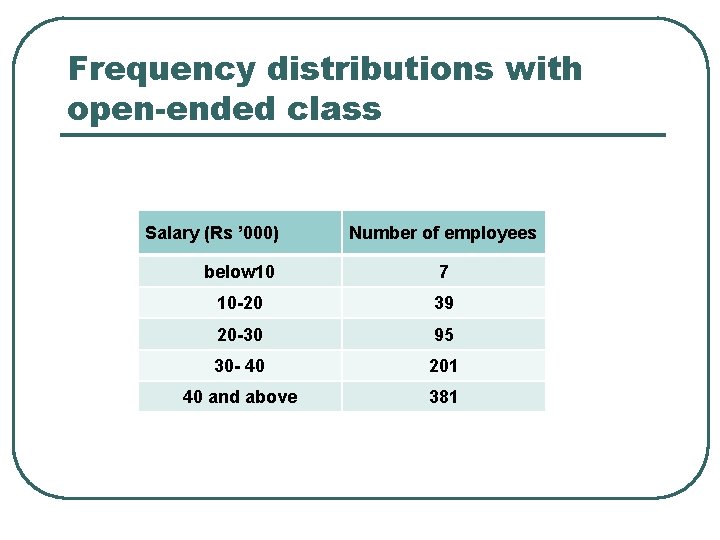
Frequency distributions with open-ended class Salary (Rs ’ 000) Number of employees below 10 7 10 -20 39 20 -30 95 30 - 40 201 40 and above 381

Frequencies are given in cumulative form (either more than type or less than type) Marks obtained Number of students Less than 10 7 Less than 20 39 Less than 30 95 Less than 40 201 Less than 50 381 Less than 60 545 Less than 70 631 Less than 80 675

Correcting Incorrect Values The mean marks of 100 students were found to be 40. Later on it was discovered that a score of 53 was misread as 83. Find the correct mean. •

Combined Arithmetic Mean • • Mean height of 25 male workers in a factory is 61 inches & the mean height of 35 female workers in the same factory is 58 inches. Find Combined mean.

Advantages of Arithmetic mean It is rigidly defined. It is easy to calculate and simple to follow. It is based on all the observations. It is readily put to algebraic treatment. It is least affected by fluctuations of sampling.

Disadvantages of Arithmetic mean The arithmetic mean is highly affected by extreme values. It cannot average the ratios and percentages properly. It cannot be computed accurately if any item is missing. The mean sometimes does not coincide with any of the observed value. It cannot be computed accurately for unequal and openended class intervals.

Weighted Arithmetic Mean It is used where the relative importance of the different items is not same. Useful in problems relating to • Construction of index numbers • Standardized birth and death rates

Weighted Arithmetic Mean A train runs 25 miles at a speed of 30 m. p. h. , another 50 miles at a speed of 40 m. p. h. , then due to repairs of track travels for 6 minutes at a speed of 10 m. p. h. and finally covers the remaining distance of 24 miles at a speed of 24 m. p. h. What is the average speed in miles per hour.

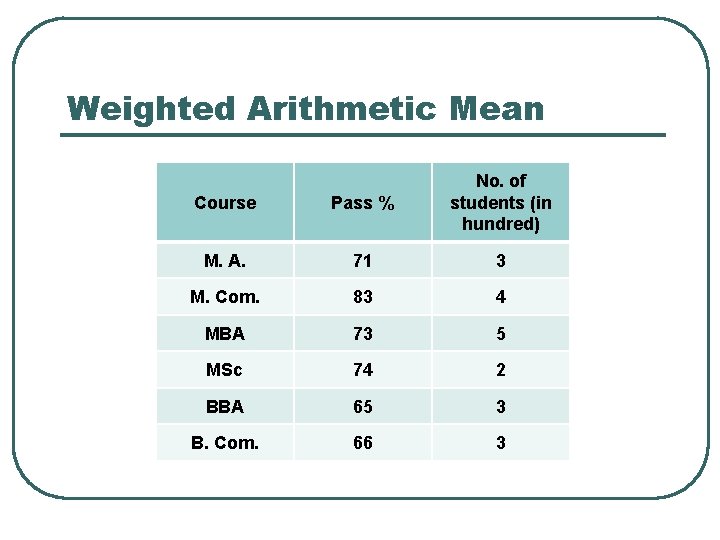
Weighted Arithmetic Mean Course Pass % No. of students (in hundred) M. A. 71 3 M. Com. 83 4 MBA 73 5 MSc 74 2 BBA 65 3 B. Com. 66 3

Geometric mean is defined as the Nth root of the product of N items.

Geometric mean Used to find average per cent increase in sales, production, population, etc. Construction of index numbers

Geometric mean The Price of a commodity increased by 5% from 2006 to 2007, 8% from 2007 to 2008 and 77% from 2008 to 2009. Calculate average increase in Prices.

Harmonic Mean It is defined as the reciprocal of the arithmetic mean of the reciprocal of individual observations.

Harmonic Mean An Aeroplane covers four sides of a square at a speed of 1000, 2000, 3000 and 4000 Km per hour. Calculate average speed.

Relationship between A. M. , G. M. & H. M A. M. > G. M. > H. M.