Measurements Significant figures Scientific Notation Dimensional analysis Significant

Measurements Significant figures Scientific Notation Dimensional analysis

Significant Figures � In the real world, no measurement is exact. The relative exactness of a measurement is its accuracy � In a measured value, all the digits that are known to be exact are called significant digits. Zeros at the end of a whole number are assumed to be nonsignificant.

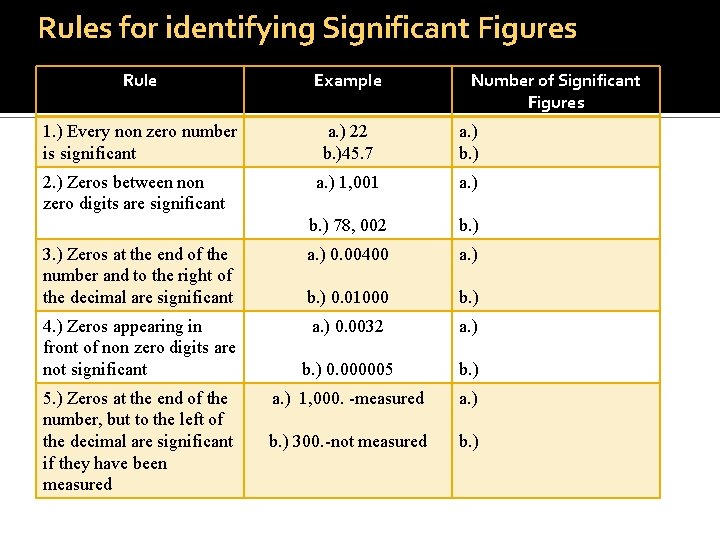
Rules for identifying Significant Figures Rule Example 1. ) Every non zero number is significant a. ) 22 b. )45. 7 a. ) b. ) a. ) 1, 001 a. ) b. ) 78, 002 b. ) a. ) 0. 00400 a. ) b. ) 0. 01000 b. ) a. ) 0. 0032 a. ) b. ) 0. 000005 b. ) a. ) 1, 000. -measured a. ) b. ) 300. -not measured b. ) 2. ) Zeros between non zero digits are significant 3. ) Zeros at the end of the number and to the right of the decimal are significant 4. ) Zeros appearing in front of non zero digits are not significant 5. ) Zeros at the end of the number, but to the left of the decimal are significant if they have been measured Number of Significant Figures

Independent Practice 9004507 m has ___ significant figures 0. 00000860092 s has __ sig. figs. 102. 00 kg has ___ sig. figs. The ruler reads 700 g, so your measurement has ___ sig. figs. 5. 1. 02 x 105 s has ___sig. figs. 1. 2. 3. 4.

Scientific Notation �Used for very large or very small numbers. �Made up of three parts: the coefficient, the base and the exponent. 567 000 in sci. notation is: 5. 67 x 105 coefficient base exponent

Standard to Sci. Notation � Move decimal as many times to make a number between 1 and 10 � Coefficient is always followed by x 10 � Exponent = number of times you move the decimal Large # = ( + )exponent Small # = ( - )exponent �Example: What is 238, 000 in Sci. Notation?

Independent Practice 1) 597800000 2) 0. 00004507 3) 250000 4) 0. 0023

Sci. Notation to Standard �Move the decimal as many times as the exponent is worth Positive exponent = move to the Negative exponent = move to the �Fill spaces with zeros �Example: What is 1. 56 x 105 notation? in Standard

Independent Practice 1) 2. 36 x 108 2) 7. 8 x 10 -3 3) 3. 92 x 10 -5 4) 5. 43 x 105

Dimensional Analysis �It is a method used to convert from one unit to another �Consists of 3 Steps to get your answer 1. ) Identify the Given and the Unknown 2. ) Identify the Conversion factor needed to go from one unit to another 3. ) Set up the problem 4. ) Multiply across at the top and divide by the bottom

Example �How many kg are in 3. 42 grams?

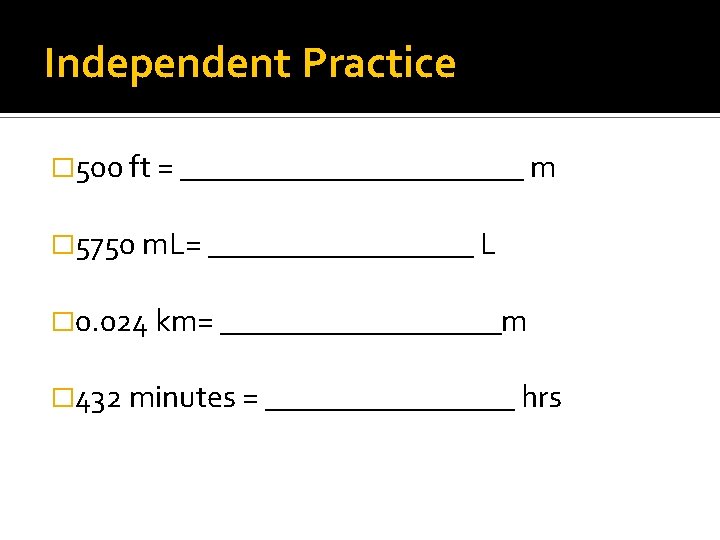
Independent Practice � 500 ft = ___________ m � 5750 m. L= _________ L � 0. 024 km= _________m � 432 minutes = ________ hrs