Measurements in Experiments Measurements in Experiments Scientists perform

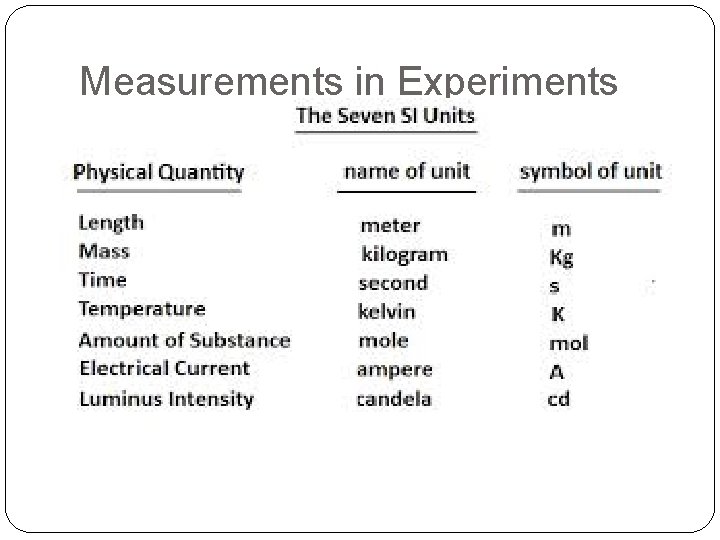
Measurements in Experiments

Measurements in Experiments �Scientists perform experiments to test how changing one variable (Independent) in a situation affects another variable (dependent). �To represent their findings accurately, numerical expression is necessary �In science, a number standing alone can have many meanings… 13 �Thirteen what? Apples? Dollars? Feet? Meters?

Measurements in Experiments �In order to better describe what is being tested, numerical representation must be accompanied by units to represent what physical quantity is being measured. �The description of “what” is being measured is called dimension �We will be working with three basic dimensions �Length �Mass �Time

Measurements in Experiments �SI is the standard measurement system for science �When scientists do research, they must be able to communicate their findings with one another �For this reason, scientists agreed upon a uniform measurement system for all scientific research and discovery �SI or Systeme International d’Unites

Measurements in Experiments �In SI, the base units of length, mass, and time are… �The meter �The kilogram �The second �Not every observation can be described using these units… However, these units can be combined to form derived units

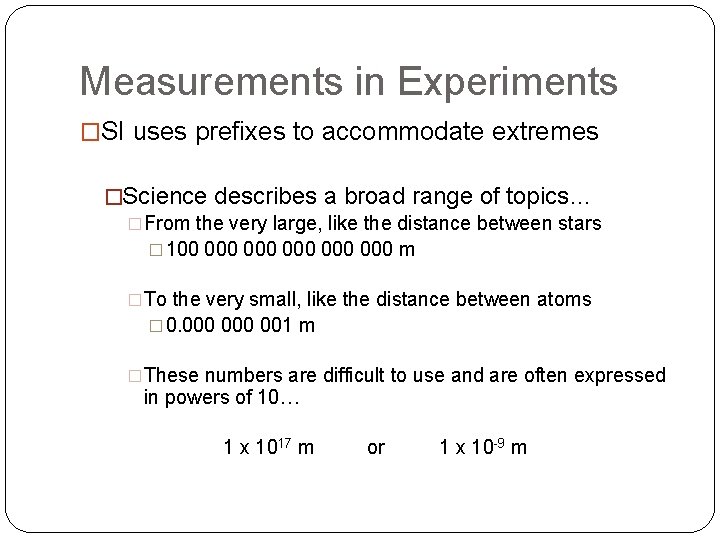
Measurements in Experiments �SI uses prefixes to accommodate extremes �Science describes a broad range of topics… �From the very large, like the distance between stars � 100 000 000 000 m �To the very small, like the distance between atoms � 0. 000 001 m �These numbers are difficult to use and are often expressed in powers of 10… 1 x 1017 m or 1 x 10 -9 m

Measurements in Experiments �Another approach is to combine units with prefixes that symbolize certain powers of 10

Measurements in Experiments �Here’s an example… �A common housefly is 5 x 10 -3 m long…or… 5 mm long �A satellite 8. 25 x 105 m above the Earth’s surface can be expressed as being 825 km

Measurements in Experiments �Conversions �Converting a measurement from its prefix form is easy to do… �Put the quantity from one side of the equation in the numerator and the other in the denominator �E. g. 1 mm 1 x 10 -3 m Because these two quantities are equal, this statement is equal to “ 1”

Measurements in Experiments �Conversion: cont… �To convert measurements, use the conversion factor that will cancel the units you are given to provide the units that you need…

Measurements in Experiments �Both dimension and units must agree �Length must be expressed in meters, not kilograms or seconds �Also, measurements and calculations should have the same units… �You cannot divide meters by centimeters!

Accuracy and Precision �Careful measurements are very important in physics �However, no measurement is perfect �In describing the imperfection, one must consider both the accuracy and the precision �Accuracy – a description of how close a measurement is to the correct or accepted value �Precision – describes the limitations of the measuring instrument or the exactness of a measurement

Accuracy and Precision �Poor accuracy involves errors that can often be corrected by examining our measurement techniques �Poor precision is typically due to limitations of the measuring instruments �For example, a measurement of 1. 325 m is more precise than a measurement of 1. 3 m. �We can often increase the precision of our measuring instruments by careful estimation

Accuracy and Precision �Significant figures help keep track of imprecision �Significant figures: the digits in a measurement that are known with certainty plus the first digit that is uncertain �E. g. A pencil’s length is measured using a ruler marked in cm. �The pencil is slightly longer than 18 cm. �We estimate it to be 18. 2 cm long �The 18 represents the “known” values while the 0. 2 is the “one estimated digit. ”