Measurements and Recording Numbers Chapter 3 Measurement MeasurementA

Measurements and Recording Numbers Chapter 3

Measurement �Measurement-A quantity that has both a number and a unit. �EX: 12. 0 feet �In Chemistry the use of very large or very small numbers is common � 1, 200, 000 or 0. 000056

Scientific Notation �Scientific Notation allows scientists to record very large or very small numbers more easily. �A given number is written as the product of 2 numbers: a coefficient and a power of 10 � 1, 200, 000 becomes => 1. 2 x 109 � 0. 000056 becomes => 5. 6 x 10 -5 � The coefficient must be a number between 1 and 9

Scientific Notation �For numbers larger than 1 the power of ten will be positive � 1, 523 1. 523 X 103 (POSITIVE EXPONENT) �For numbers lass than 1, the power of ten will be negative � 0. 025 2. 5 X 10 -2 (NEGATIVE EXPONENT) �The number of places the decimal has moved will be indicated by the number on the power � 1, 523 The decimal moves 3 places to the left � 0. 025 The decimal moves 2 places to the right

Practice Convert to scientific notation 1. 1, 234, 432 2. 0. 00034 3. 142 4. 1542 5. 0. 002 6. 0. 00000056 �Answers 1. 2. 3. 4. 5. 6. 1. 234432 x 106 3. 4 x 10 -4 1. 42 x 102 1. 542 x 103 2 x 10 -3 5. 6 x 10 -7

International System of Units �All measurement depends on UNITS that serve as a reference �Metrics are used because the use and conversion of is easier than other systems �The metric system was established in 1795 in France �There are 7 base units

The International System of Units �Table 1. SI base units SI base unit Base quantity Name 1. Length meter 2. Mass kilogram 3. time second 4. electric current ampere 5. temperature Kelvin 6. amount of substance mole 7. luminous intensity candela Symbol m kg s A K mol cd

Metric Prefixes �Mega M 1, 000 �Kilo k 1, 000 �Hecto h 100 �Deka da 10 �Base Units 1 �Deci d 0. 1 �Centi c 0. 01 �Milli m 0. 001 �Micro µ 0. 000, 001 �Nano n 0. 000, 001 �Prefixes are used when units of measurement are much larger or smaller than the base unit.

Metric Conversion using the Stairstep Method

How Do I Use This? 5. 0 K m _? _ m �-The first letter of the prefix in the unit of measurement tells you which step to start on. �-The first letter in the second unit of measurement tells you which step to stop on. �-Find which step to start on, and count the number of steps it takes to get to the step that you need to stop on.

10 Kg…? g K � 3 steps right H �Move the decimal 3 spaces right D � 10 Kg becomes… � 10, 000 g 1000 g ram G r e r Lit e M d c m

Measurements and Their Uncertainty Using and Expressing Measurement

Accuracy and Precision �Accuracy is a measure of how close a measurement comes to the actual or true value of an object. �EX: Throw one dart and hit the bulls eye this throw is considered accurate. �Precision is a measure of how close a series of measurements are to one another. �Several measurements are taken: 1. 2, 1. 5, 1. 8 (these are NOT precise) �Several measurements are taken: 2. 5, 2. 6 (These measurements ARE precise)

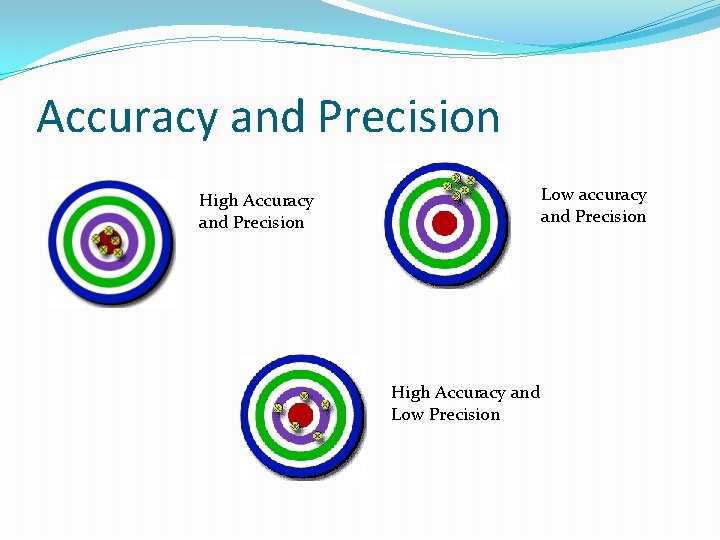
Accuracy and Precision Low accuracy and Precision High Accuracy and Low Precision

Uncertainty and Error �Uncertainty refers to the range of possible values within which the true value of the measurement lies. �Error means the difference between a measured value (what you measured) and the true value for a measurement.

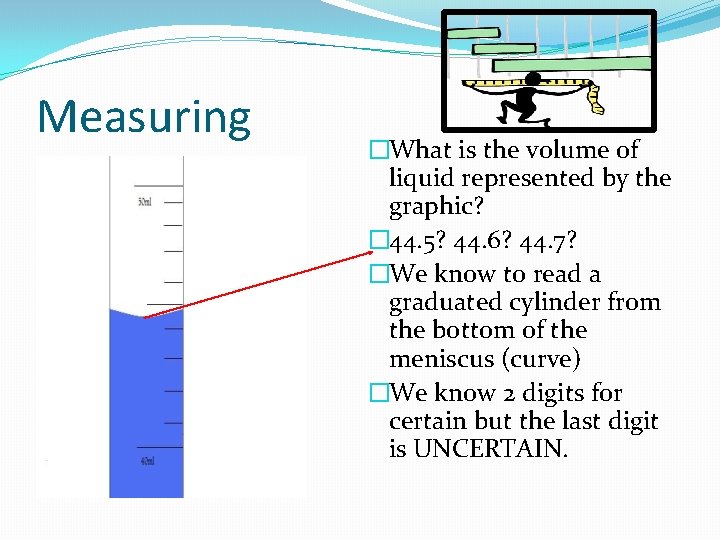
Measuring �What is the volume of liquid represented by the graphic? � 44. 5? 44. 6? 44. 7? �We know to read a graduated cylinder from the bottom of the meniscus (curve) �We know 2 digits for certain but the last digit is UNCERTAIN.

Determining Error �When determining error in a measurement we compare the experimental value to the actual(theoretical) value. Also called the accepted value! �The differnce between the two values is called the error and is an absolute value. Formula for Percent Error

Sources of Error �The measuring device �How YOU measure �Elimination of error is accomplished by multiple trials

Percent Error �EXAMPLE: A student measures the density of lead to be 11. 23 g/m. L. The actual value is 11. 4 g/m. L. Calculate the percent error. � 1. 11. 23 -11. 4 = - 0. 16 (absolute value) � 0. 16/11. 4 = 0. 014 � 0. 014 x 100 = 1. 4 % error

Significant Figures Chapter 3

�In a measurement the last digit is considered to be an estimate (guess). �Significant figures in a measurement include those numbers that are known plus one estimates digit.

� 1) ALL non-zero numbers (1, 2, 3, 4, 5, 6, 7, 8, 9) are ALWAYS significant. � EX: 12. 543 has 5 Sig. Figs. � 2) ALL zeroes between non-zero numbers are ALWAYS significant. “Captured Zeros” � EX 1. 02 has 3 Sig. Figs. � 3) ALL zeroes which are “Place Holders” are NOT significant. � EX: 0. 0023 has 2 Sig. Figs. � EX: 100 has 1 Sig. Fig. [No decimal = place holder] � 4) ALL zeroes which are to the left of a written decimal point and are in a number >= 10 are ALWAYS significant. “Trailing Zeros” � EX: 12. 00 has 4 Sig. Figs.

Determine the number of significant digits in each of the following: a) 6. 571 g b) 0. 157 kg c) 28. 0 ml d) 2500 m e) 0. 0700000 g

Rule #1: ADDITION AND SUBTRACTION: When adding or subtracting numbers, count the NUMBER OF DECIMAL PLACES to determine the number of significant figures. Record your answer using the FEWEST NUMBER of decimal places 23. 112233 (6 places after the decimal) 1. 3324 (4 places after the decimal) + 0. 25 (2 places after the decimal) 24. 694633 (on calculator) Answer: 24. 69 (rounded to 2 places in the answer)

Rule #MULTIPLICATION AND DIVISION: When MULTIPLYING OR DIVIDING numbers, count the NUMBER OF SIGNIFICANT FIGURES to determine the number of significant figures. Record your answer using the FEWEST NUMBER of significant figures 12. 3 x 1. 5 3 sig figs 2 sig figs = 18. 45 calculator answer Answer: 18 (rounded to 2 significant figures in the answer)

Using the rules for Significant figures calculate the following and record using the correct significant figures. a) 16. 5 + 8 + 4. 37 b) 13. 57 - 6. 3 c) 3. 15 x 2. 5 x 4. 00 d) 40. 8 / 5. 05

Dimensional Analysis Converting between units!

Conversions �A ratio of equivalent measurements �Ex. 1 foot = 12 in �Ex. 1 in = 2. 54 cm �Ex. 1 kg = 1000 g �When a measurement is multiplied by a conversion factor, the numerical value is generally changed, but the actual size of the quantity measured remains the same.

How do we use conversion factors? �Conversions allow us to convert between units of measurements! �How many inches are in 2. 5 feet? �We know 12 inches = 1 foot Answer: 2. 5 ft x 12 inches = 48 in 1 ft We can use the same t-chart for these conversions that we used t 0 convert between pressure units Units of feet must cancel!!

Practice �How many seconds are in 2. 5 hours? �Find your conversion factor! � 3600 seconds = 1 hour �Set up the problem 2. 5 hr 3600 s 1 hr �Solve: 2. 5 x 3600 = 9000 s

More Practice �How many inches are found in 4. 3 cm? � 1 in = 2. 54 cm is the equality � 4. 3 cm 1 in � = 2. 54 cm � Solve: 4. 3/2. 54 = 1. 6929 = 1. 7 inches (includes sig figs)

Multistep Conversions �How many meters are found in 11. 2 miles? �We need two equalities � 1 mile = 1. 6093 km � 1 km = 1000 m 11. 2 miles 1 mile 1. 6093 km 1000 m 1 km Solve: (11. 2 x 1000)/ 1. 6093 = 6959. 5 = 6960 m (correct sig figs)

Temperature Conversions Fahrenheit Celsius Kelvin

Temperature �Measures the average kinetic energy of a particle. �Non-SI temperature scale is Fahrenheit �The temperature scales used in science are Celsius and Kelvin �Kelvin is the SI base unit for temperature �It is a conversion not an actual measureable scale. Formula: K= °C + 273 Formula: °C = K - 273

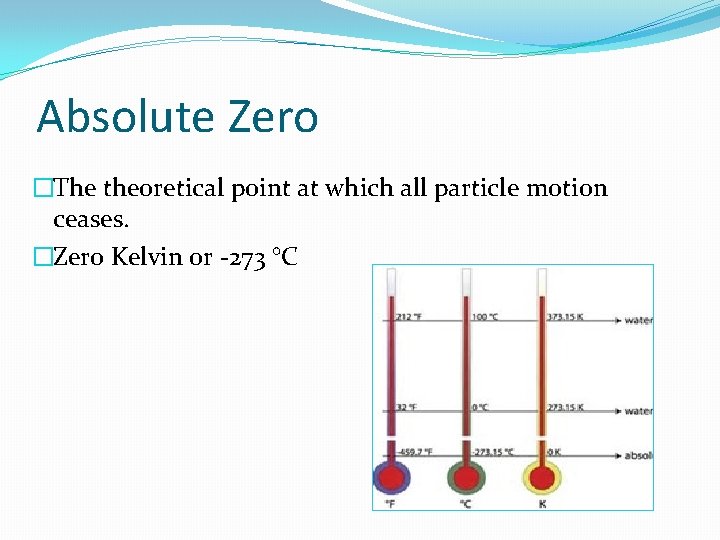
Absolute Zero �The theoretical point at which all particle motion ceases. �Zero Kelvin 0 r -273 °C

Conversions from Celsius to Kelvin K = °C + 273 1. 20° C = ? ? K 2. -5. 0 °C = ? ? K 3. 103. 0 °C = ? ? K �Answers 1. 293 K 2. 268 K 3. 376 K

Converting from Kelvin to Celsius °C = K – 273 1. �Answers 1. -23. 0° C 250 K 2. -258° C 2. 15 K 3. 177 °C 3. 450 K

Density

Density �Density is the mass per unit volume of an object. �Density is an intensive property…It depends of the composition of the substance, not the size of the sample! �Density of an object changes as temperature changes �As temperature goes up, density goes down.

Density formula �Density = Mass / volume �Units: �g/m. L (liquids) �g/cm 3 (solids)

Density problems �A copper penny has a mass of 3. 1 g and a volume of 0. 35 cm 3 What is the density of the penny? �D = ? �m = 3. 1 g �v = 0. 35 cm 3 �D = 3. 1 g / 0. 35 cm 3 �D = 8. 8571 g/cm 3 �D = 8. 9 g/cm 3 (correct sig figs)

Density Problems A metal sample has a Density of 11. 39 g/m. L and a mass of 7. 01 g. What is the volume of the metal? �D= 11. 39 g/m. L �m = 7. 01 g �v = ? ? ? 11. 39 = 7. 01 X X = 7. 01/ 11. 39 = 0. 615452151 = 0. 615 m. L (correct sig figs)