MEASUREMENT Units of Measurement SI unit and derived

MEASUREMENT Units of Measurement : SI unit and derived units Unit prefixes Unit conversion using dimensional analysis Scientific notation Increment, Accuracy, Precision

OBJECTIVES Distinguish between a number and a quantity. Name SI units for length, mass, time, temperature, volume and density. Define and identify base units; unit conversions; identify prefixes Perform unit conversion using dimensional analysis.

Units of Measurement • In our daily lives we deal with making measurements routinely. –i. e. , How much gasoline is required to fill your gas tank? What time did you wake up this morning? How fast did you drive to school today ? • Doctors, nurses, pharmacists–Doctors and nurses make measurements constantly. Measurements like pulse rate, blood pressure, temperature, drug dosage. • Math - The language of Science –Scientists make countless measurements during their experiments to prove or disprove a theory.

Units of Measurement What is your response if I told you that: I weigh 65 In any measurement magnitude (the number) as well as the unit (meaning) must be stated. Otherwise, it is meaningless!

Number vs. Quantity • Quantity : number + unit UNITS MATTER!!

Systems of Measurement What units are used? The Rest of the World America English System 1 ft = 12 in 1 yd= 3 ft 1 mi. = 1, 760 Yd 1 mi = 5280 ft Metric System 1 km = 1000 m 1 m = 100 cm Scientific Community Le System International d’Unites SI Units are basically an updated form of the metric system.

Metric system and the Le Systeme International d'Unites (SI) • The Metric system is convenient because it uses only one fundamental unit for each type of measurement. For example for: *Length we use only meter, in the US we use foot, yard, inch. *Mass we use Kg not pound. • All the Prefixes are multiples of 10.

SI Units Quantity Symb Base Unit Abbre ol v. l Length meter m Mass m kilogram kg Time t second s Temp T kelvin K n mole mol Amount of

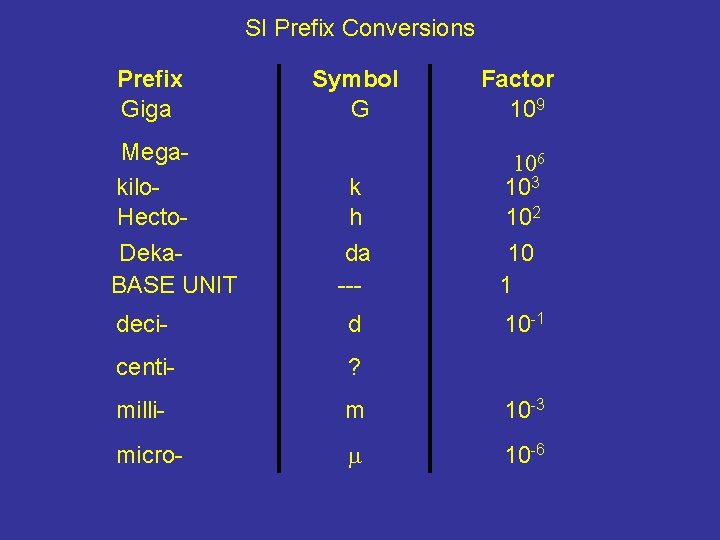
SI Prefix Conversions Prefix Giga Symbol G Factor 109 k h da --- 106 103 102 10 1 deci- d 10 -1 centi- ? milli- m 10 -3 micro- 10 -6 Megakilo. Hecto. Deka. BASE UNIT

Derived Units: Combination of base units • Area ( m 2) • length = m x m • Volume (m 3) – length= m x m • Density (g/cm 3) – mass per volume M D= V

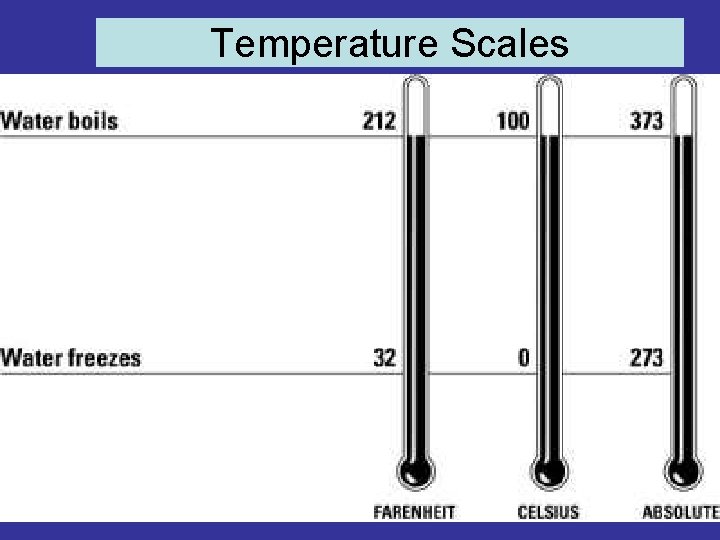
Temperature A measure of how hot or how cold an object is. SI Unit: the kelvin • Note: not a degree • Absolute Zero= 0 K (K)

Temperature Scales

Celsius and Kelvin K= o. C + 273

Density • An object has a volume of 825 cm 3 and a density of 13. 6 g/cm 3. Find its mass. GIVEN: WORK: V = 825 cm 3 D = 13. 6 g/cm 3 M=? M = DV M = (13. 6 g/cm 3)(825 cm 3) M = 11, 200 g

Density • A liquid has a density of 0. 87 g/m. L. What volume is occupied by 25 g of the liquid? GIVEN: WORK: D = 0. 87 g/m. L V=? M = 25 g V=M D V= 25 g 0. 87 g/m. L V = 29 m. L

Unit 1 - MEASUREMENT Unit conversion using dimensional analysis Page

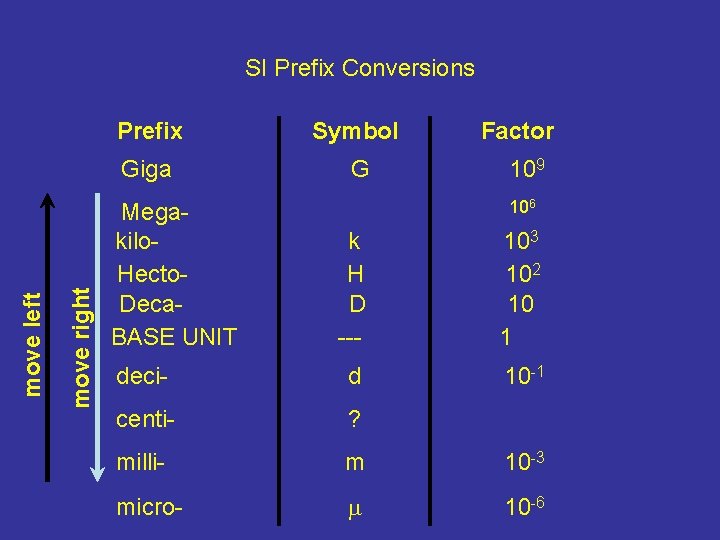
SI Prefix Conversions 1. Find the difference between the exponents of the two prefixes. 2. Move the decimal that many places. To the left or right?

move right move left SI Prefix Conversions Prefix Symbol Giga G Megakilo. Hecto. Deca. BASE UNIT Factor 109 106 k H D --- 103 102 10 1 deci- d 10 -1 centi- ? milli- m 10 -3 micro- 10 -6

SI Prefix Conversions 1) 20 cm = ______ m 2) 0. 032 L = _______ m. L 3) 45 m = _______ cm 4) 80. 5 km = _______ m

How would you convert 2 h 45 min to second Convert 55. 00 km/h to m/s

Converting by using Dimensional Analysis • Steps: 1. Identify starting ( also called given, old )& ending ( target, new) units. 2. Line up conversion factors so units cancel. ( hint : the new units should on the top) 3. Multiply all top numbers & divide by each bottom number. ( ) 4. Check units & answer.

Converting by using Dimensional Analysis: inch to cm Identify 10. 0 in We start by writing down the Given (old) and its Unit

Converting by using Dimensional Analysis: inch to cm Line up 10. 0 in x 2. 54 cm 1 in We know 1 in = 2. 54 cm. So our conversion factor is : 1 in = 2. 54 cm. Since we want to convert to cm, it goes on the top. ( Hint)

Converting by using Dimensional Analysis: inch to cm Cancel units 2. 54 cm 10. 0 in x 1 in Now we cancel and collect units. The inches cancel out, leaving us with cm : the Target unit.

Converting by using Dimensional Analysis: inch to cm 10. 0 in x 2. 54 cm = 25. 4 cm 1 in Since the unit is correct, all is left to do the math. . . The Answer

Lets check it out !!!!!! Find the 10 in mark and directly across at the cm side. What number do you find?

Converting by using Dimensional Analysis: inch to cm 5) You go to Europe and decide to have a haircut. Your hairdresser wants to cut your hair 8. 0 cm shorter. How many inches will he be cutting off? Identify , line up, cancel out, multiply, check 8. 0 cm 1 in 2. 54 cm = ? in Question: Is the conversion Factor the same? What’s the difference?

Converting by using Dimensional Analysis: g to Kg • Convert 250 g into Kg Identify , line up, cancel out, multiply, check 250 g x 1 Kg 1000 g = Kg

Converting by using Dimensional Analysis: Kg to g • Convert 1. 5 Kg into g • Identify : Given and Target unit • Line up: Conversion Factor 1. 5 kg x = g Q: Which conversion factor will you be using? 1 Kg = 1000 g or 1000 g= 1 Kg

A more complex conversion km to m hr s kilometers into meters and hour into second. We can do both conversions at once using the same method as in the previous conversion.

A more complex conversion km to m Identify 80 km hr hr s Write down the _____and ____

A more complex conversion km to m hr s Line up 1 hr 80 km x hr 3600 s First conversion factor is: 1 hour = 3600 sec.

A more complex conversion km to m Line up hr s 80 km x 1 hr x 1000 m hr 3600 s 1 km The second conversion factor is: 1 km = 1000 m.

A more complex conversion km to m Cancel out units hr s 80 km x 1 hr x 1000 m hr 3600 s 1 km m = s Check your units !!! If you have chosen the correct conversion factors, you should only be left with the units you want to convert to.

A more complex conversion km to m hr s 80 km x 1 hr x 1000 m hr 3600 s 1 km 80, 000 m = 3600 s m s = The Answer!!

A Very more complex conversion to finish at home today !! Problem 1: Convert 1 year into seconds year seconds 1 y = 1 y 365 days 24 h 1 h 1 day 60 s s

Dimensional Analysis Problem 2: Taft football needs 550 cm for a 1 st down. How many yards is this? cm yd 550 cm = 1 yd 1 in 12 in 3 ft 2. 54 cm 1 ft yd

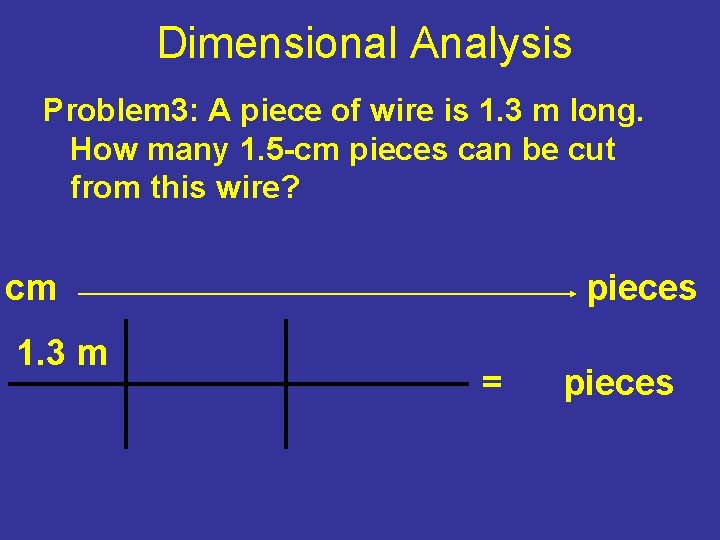
Dimensional Analysis Problem 3: A piece of wire is 1. 3 m long. How many 1. 5 -cm pieces can be cut from this wire? cm 1. 3 m pieces = pieces

Dimensional Analysis • Problem 5: How old are you in minutes? Age in y = min

Homework Units and Conversions HW Due: tomorrow How would you convert 2 h 45 min to second Convert 55. 00 km/h to m/s

Scientific Notation Mx n 10 • M is the coefficient 1<M<10 • 10 is the base • n is the exponent or power of 10

Other Examples: 5. 45 E+6 5. 45 x 10^6

Numbers less than 1 will have a negative exponent. Numbers bigger than 1 will have a positive exponent. A millionth of a second is: 0. 000001 sec 1. 0 E-6 1. 0 x 10^-6

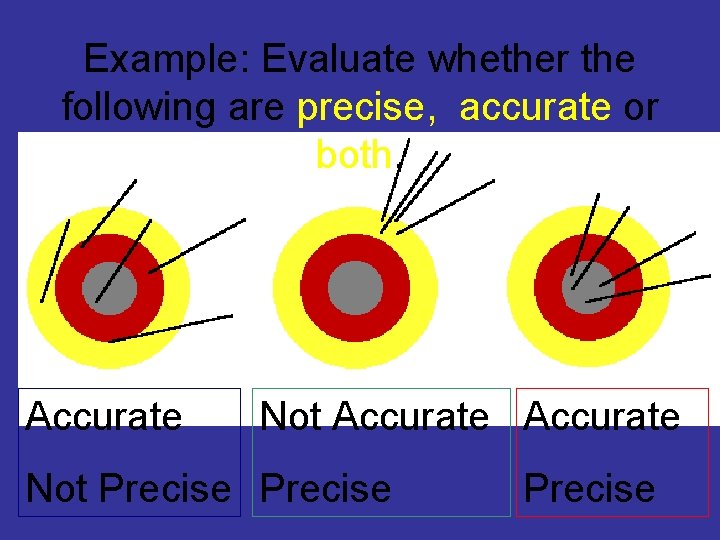
Limits of Measurement • Accuracy and Precision

• Accuracy - a measure of how close a measurement is to the true value of the quantity being measured.

Example: Accuracy • Who is more accurate (Susan or Amy) when measuring a book that has a true length of 17. 0 cm? Susan: 18. 1 cm, 16. 0 cm, 18. 0 cm, 17. 1 cm Amy: 16. 5 cm, 16. 0 cm, 16. 2 cm, 16. 3 cm

• Precision – a measure of how close a series of measurements are to one another. A measure of how exact a measurement is regardless is it is close to the real value.

Example: Precision Who is more precise when measuring the same 17. 0 cm book? Susan: 17. 0 cm, 16. 0 cm, 18. 0 cm, 15. 0 cm Amy: 15. 5 cm, 15. 0 cm, 15. 2 cm, 15. 3 cm

Example: Evaluate whether the following are precise, accurate or both. Accurate Not Precise

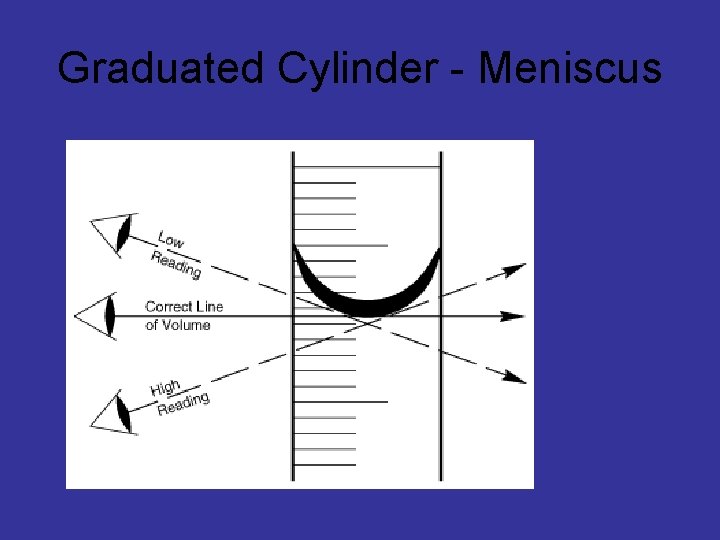
Graduated Cylinder - Meniscus