Measurement Theory Applying measurement theory to software Measurement

Class Discussion u What is scale type of Mc. Cabe’s cyclomatic number? Measurement -

Empirical Relations u One cludge that appears very often in the computer science literature

Creating a New Theory Why should a theory devised for physical phenomenon be useful

MOM u Model - Order - Mapping u the model is the abstraction u

Abstractions and Orders u We need to find an abstraction and an ordering on

Artificial u Software has been described as an artificial science because we control the

Transformations u Consider the transformations that you can do to a syntactically correct program

Triangle Problem cin>>a>>b>>c; type=“scalene”; if (a==b||b==c||a==c) type=“isosceles”; if (a==b&&b==c) type=“equilateral”; if (a>=b+c||b>=a+c||c>=a+b) type=“not a

Formal Spec u CFG is described by set of nodes {1, 3 b, 4

Partial Order u Originally, for all cfg x, y, x <=y if and only

Representation Condition u Can prove that for all cfg’s x and y, if x<=y

Proof of monotonicity u Can show that no additive transform can decrease the cfg

LCOM Lack of Cohesion in Methods Measurement - part 3 16

Metric 6: LCOM u Lack of Cohesion in Methods u Let Ii be the

What Abstraction? u Needs to highlight which attributes are used by which functions Measurement

Mapping to Abs u How does class get mapped to abstraction? Measurement - part

What transformations? u Add an attribute u Add a statement with attribute ref u

Mapping Abs to Ans u What is the mapping from the abstraction to the

Rep Condition u Does the mapping between the partial order on the abstraction and

Scale Types u Which scale type is implied by the transformations, abstraction and mapping?

Slides: 23

Download presentation

Measurement Theory Applying measurement theory to software Measurement - part 3 1

Class Discussion u What is scale type of Mc. Cabe’s cyclomatic number? Measurement - part 3 2

Empirical Relations u One cludge that appears very often in the computer science literature is to define the empirical relation as that which makes the representation condition hold for the measure u The truth is that we do not have centuries of consensus on the empirical relationships Measurement - part 3 3

Creating a New Theory Why should a theory devised for physical phenomenon be useful for software - an artificial phenomenon? Measurement - part 3 4

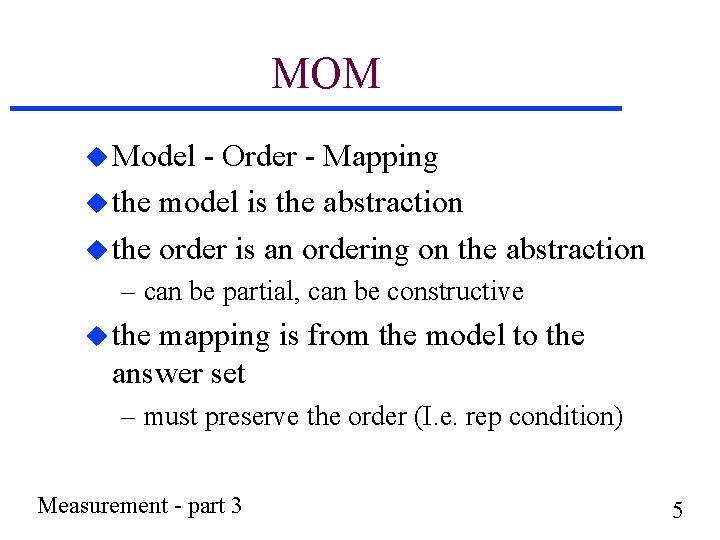
MOM u Model - Order - Mapping u the model is the abstraction u the order is an ordering on the abstraction – can be partial, can be constructive u the mapping is from the model to the answer set – must preserve the order (I. e. rep condition) Measurement - part 3 5

MOM Measurement - part 3 6

Abstractions and Orders u We need to find an abstraction and an ordering on that abstraction Measurement - part 3 7

Artificial u Software has been described as an artificial science because we control the objects. In fact, the objects are artifacts - made by humans u However, if there are constraints on these artifacts, it is usually in the operations that can change the artifacts Measurement - part 3 8

Transformations u Consider the transformations that you can do to a syntactically correct program that maintains the correctness: – – – add a statement add a condition remove a statement Measurement - part 3 9

Triangle Problem cin>>a>>b>>c; type=“scalene”; if (a==b||b==c||a==c) type=“isosceles”; if (a==b&&b==c) type=“equilateral”; if (a>=b+c||b>=a+c||c>=a+b) type=“not a triangle”; if (a<=0||b<=0||c<=0) type=“bad inputs”; cout<<type; Measurement - part 3 10

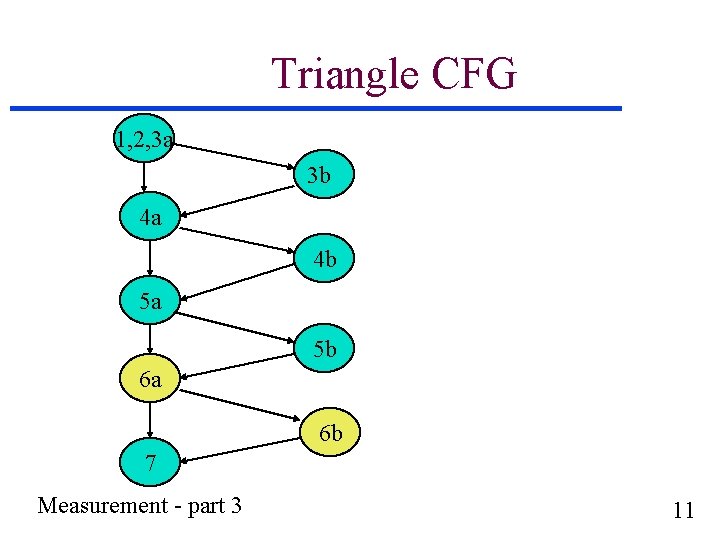
Triangle CFG 1, 2, 3 a 3 b 4 a 4 b 5 a 5 b 6 a 6 b 7 Measurement - part 3 11

Formal Spec u CFG is described by set of nodes {1, 3 b, 4 a, 4 b, 5 a, 5 b, 6 a, 6 b, 7} and set of arcs {(1, 3 b), (1, 4 a), (3 b, 4 a), (4 a, 4 b), (4 a, 5 a), (4 b, 5 a), (5 a, 5 b), (5 a, 6 a), (5 b, 6 a), (6 a, 6 b), (6 a, 7), (6 b, 7) Measurement - part 3 12

Partial Order u Originally, for all cfg x, y, x <=y if and only if all nodes and edges in x are also in y. u Thus adding an edge to x made a new cfg y such that x <= y but y may not be a cfg for a valid program u Constructive definition - x <= y if there is a set of transforms (additive) such that the transforms are applied to x produce y Measurement - part 3 13

Representation Condition u Can prove that for all cfg’s x and y, if x<=y then m(x) <= m(y) u Note that this is not the iff rep condition. Since the partial orders on the abstractions are partial, if can only be one way Measurement - part 3 14

Proof of monotonicity u Can show that no additive transform can decrease the cfg or the value of the mapping u Can show that additive transforms of adding if-then, if-then-else, while will always result in an increase of 1 in the value of the mapping Measurement - part 3 15

LCOM Lack of Cohesion in Methods Measurement - part 3 16

Metric 6: LCOM u Lack of Cohesion in Methods u Let Ii be the set of instance variables used by method i u Let P be set of pairwise null intersections of Ii u Let Q be set of pairwise nonnull intersections u LCOM = max( |P| - |Q|, 0 ) Measurement - part 3 17

What Abstraction? u Needs to highlight which attributes are used by which functions Measurement - part 3 18

Mapping to Abs u How does class get mapped to abstraction? Measurement - part 3 19

What transformations? u Add an attribute u Add a statement with attribute ref u Add a statement without attribute ref u Add a function Measurement - part 3 20

Mapping Abs to Ans u What is the mapping from the abstraction to the answer set? Measurement - part 3 21

Rep Condition u Does the mapping between the partial order on the abstraction and the answer set satisfy the representation condition (one way)? Measurement - part 3 22

Scale Types u Which scale type is implied by the transformations, abstraction and mapping? Measurement - part 3 23