Measurement Reliability QianLi Xue Biostatistics Program Harvard Catalyst

Measurement Reliability Qian-Li Xue Biostatistics Program Harvard Catalyst | The Harvard Clinical & Translational Science Center Short course, October 27, 2016

Objectives • Classical Test Theory • Definitions of Reliability • Types of Reliability Coefficients – Test-Retest, Inter-Rater, Internal Consistency, – Correction for Attenuation • Review Exercises

What is reliability • Consistency of measurement • The extent to which a measurement instrument can differentiate among subjects • Reliability is relative

Facets of Reliability • Mrs. Z scores 20 at visit 1 and 25 at visit 2. Could be: • Random variation – (Test-Retest) • Tech # 2 more lenient than Tech # 1 – (Inter-Rater Reliability) • Version # 2 easier than Version # 1 – (Related to Internal Consistency) • Mrs. Z’s picture-naming actually improved

Classical Test Theory • X = Tx + e • The Observed Score = True Score + Error • Assumptions: – E(e) = 0 – Cov(Tx, e) = 0 – Cov(ei, ek) = 0 • Var(X) =Var(Tx+e) = Var(Tx) + 2 Cov(Tx, e)+Var(e) • Var(X) = Var(Tx) + Var(e)

Reliability as Consistency of Measurement • The relationship between parallel tests • Ratio of True score variance to total score variance ρxx = Var(Tx) = Var(X)-Var(e) Var(X)

Parallel Tests • Parallel: • Tau-Equivalent: • Essentially Tau-Equivalent: • Congeneric: See Graham (2006) for details.

Correlation, r Correlation (i. e. “Pearson” correlation) is a scaled version of covariance -1 ≤ r ≤ 1 r=1 perfect positive correlation r = -1 perfect negative correlation r = 0 uncorrelated

Correlation between Parallel Tests • equal to reliability of each test

DIADS Example • Depression in Alzheimers Disease Study. • Placebo-controlled double-blind controlled trial of sertraline • One outcome was the Boston Naming Test. • Consists of 60 pictures to be named, two versions.

Measures for Reliability Continuous Categorical Test-retest r or ICC Kappa or ICC Inter-rater r or ICC Kappa or ICC Internal Consistency Alpha or Split-half or ICC KR-20 or ICC (dichotomous)

Kappa Coefficient (Cohen, 1960) • Test-Retest or Inter-rater reliability for categorical (typically dichotomous) data. • Accounts for chance agreement

Kappa Coefficient kappa = Po - Pe Po = observed proportion of agreements 1. 0 - Pe Pe = expected proportion of agreements kappa = [(20+55)/100]-[(10. 5+45. 5)/100] = 0. 43 1 -[(10. 5+45. 5)/100]

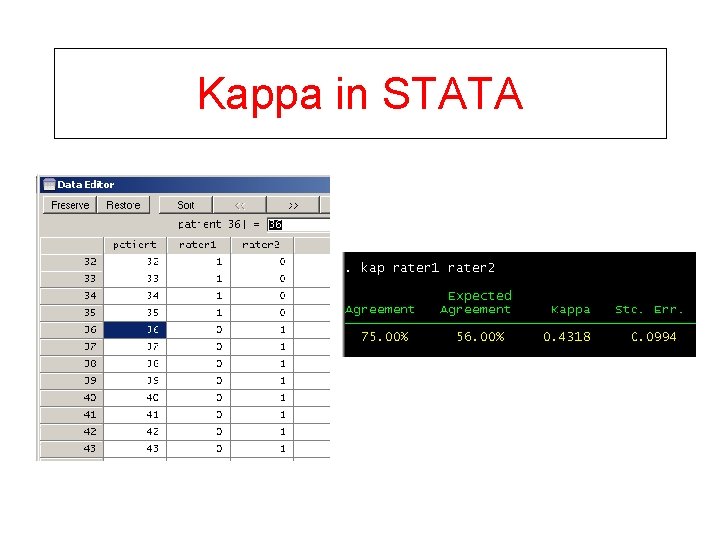
Kappa in STATA

Kappa Interpretation • Interpretation: Kappa Value Interpretation Below 0. 00 Poor 0. 00 -0. 20 Slight 0. 21 -0. 40 Fair 0. 41 -0. 60 Moderate 0. 61 -0. 80 Substantial 0. 81 -1. 00 Almost perfect (source: Landis, J. R. and Koch, G. G. 1977. Biometrics 33: 159 -174) • kappa could be high simply because marginal proportions are either very high or very low!! • Best interpretation of kappa is to compare its values on other, similar scales

Weighted Kappa (Cohen, 1968) • For ordered polytomous data • Requires assignment of a weighting matrix • Kw=ICC with quadratic weights (Fleiss & Cohen, 1973)

Measures for Reliability Continuous Categorical Test-retest r or ICC Kappa or ICC Inter-rater r or ICC Kappa or ICC Internal Consistency Alpha or Split-half or ICC KR-20 or ICC (dichotomous)

Internal Consistency • Degree of homogeneity of items within a scale. • Items should be correlated with each other and the total score. • Not a measure of dimensionality; assumes unidimensionality.

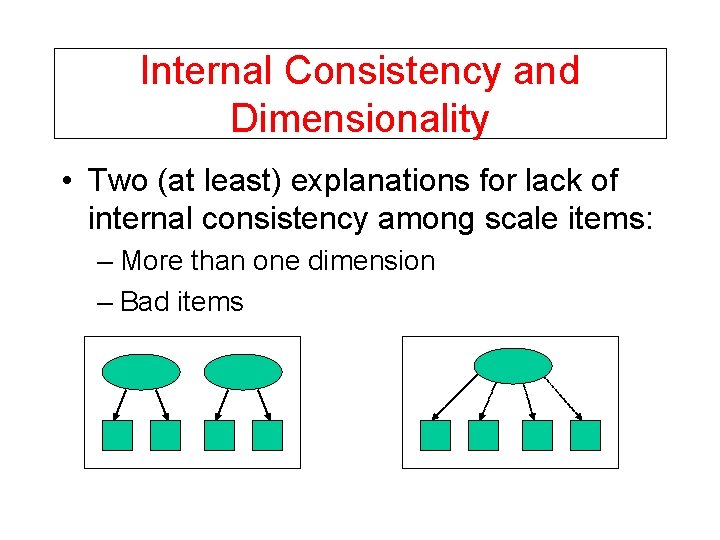
Internal Consistency and Dimensionality • Two (at least) explanations for lack of internal consistency among scale items: – More than one dimension – Bad items

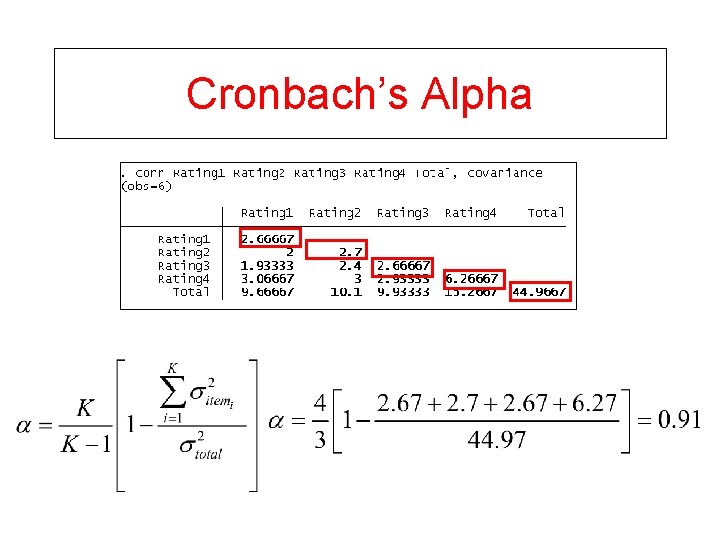
Cronbach’s Alpha

Cronbach’s Alpha • Mathematically equivalent to ICC(3, k) • When inter-item correlations are equal across items, equal to the average of all split-half reliabilities. See De. Vellis pp 36 -38

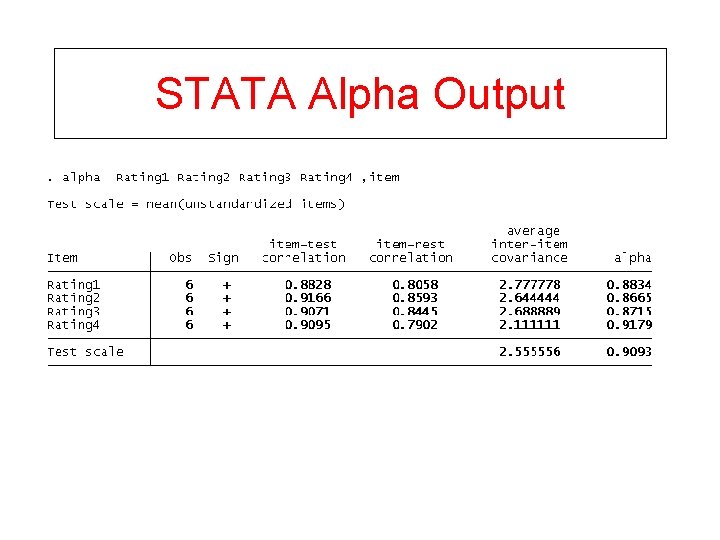
STATA Alpha Output

Kuder-Richardson 20 Proportion responding positively to item i • Cronbach’s alpha for dichotomous items • Use alpha command in STATA, will automatically give KR 20 when items are dichotomous.

Correction for Attenuation • You can calculate rx, y • You want to know r. Tx. Ty

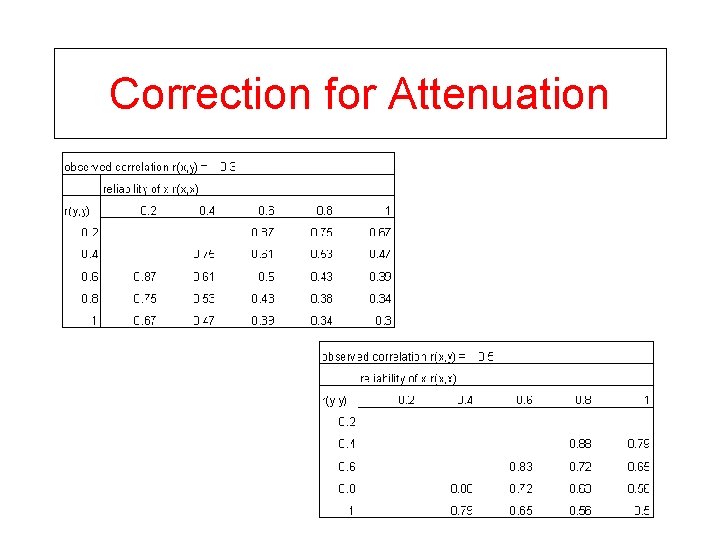
Correction for Attenuation

How to Improve Reliability • Reduce error variance – Better observer training – Improve scale design • Enhance true variance – Introduce new items better at capturing heterogeneity – Change item responses • Increase number of items in a scale

Exercise #1 • You develop a new survey measure of depression based on a pilot sample that consists of 33% severely depressed, 33% mildly depressed, and 33% non-depressed. You are happy to discover that your measure has a high reliability of 0. 90. Emboldened by your findings, you find funding and administer your survey to a nationally representative sample. However, you find that your reliability is now much lower. Why might have the reliability dropped?

Exercise #1 - Answer Suppose all of the national sample are severely depressed, then BMS (between-person variance) drops, as does ICC.

Exercise #2 • A: Draw data where the cov(Tx, e) is negative • B: Draw data where the cov(Tx, e) is positive

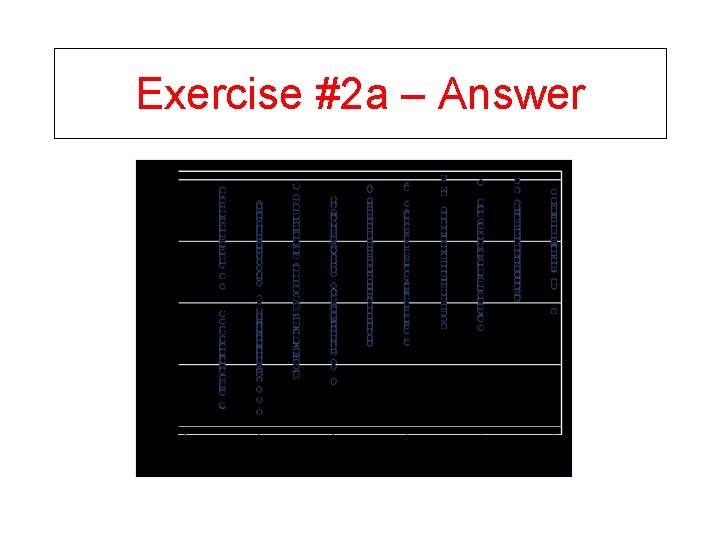
Exercise #2 a – Answer

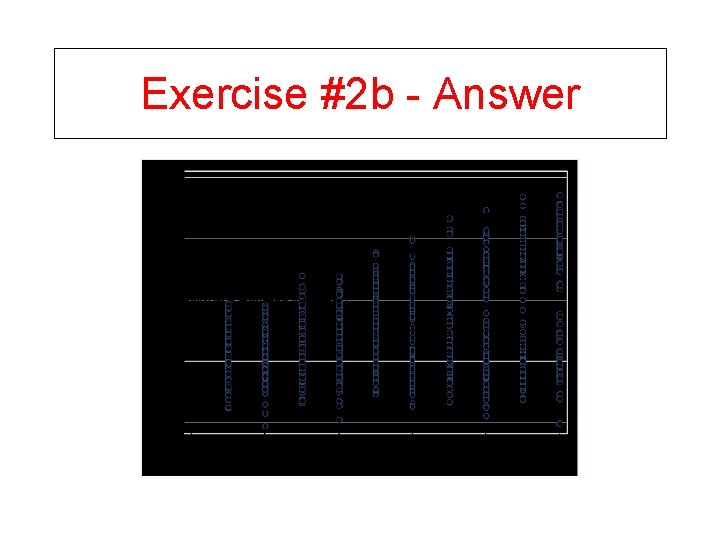
Exercise #2 b - Answer

Exercise #3 • The reported correlations between years of educational attainment and adults’ scores on anti-social personality disorder scales (ASP) is usually about 0. 30, and the reported reliability of the education scale is 0. 95 and for the ASP scale 0. 70. What will your observed correlation between these two measures be if your data on the education scale has the same reliability (0. 95) but the ASP has much lower reliability of 0. 40?

Exercise #3 - Answer • Solve for true score correlation from reported data. • Solve for new observed correlation

Exercise #4 • In rating a dichotomous child health outcome among 100 children, two psychiatrists disagree in 20 cases – in 10 of these cases the 1 st psychiatrist rated the outcome as present and the 2 nd as absent, and in the other 10 cases were vice-versa. What will be the value of the Kappa coefficient if both psychiatrists agree that 50 children have the outcome?

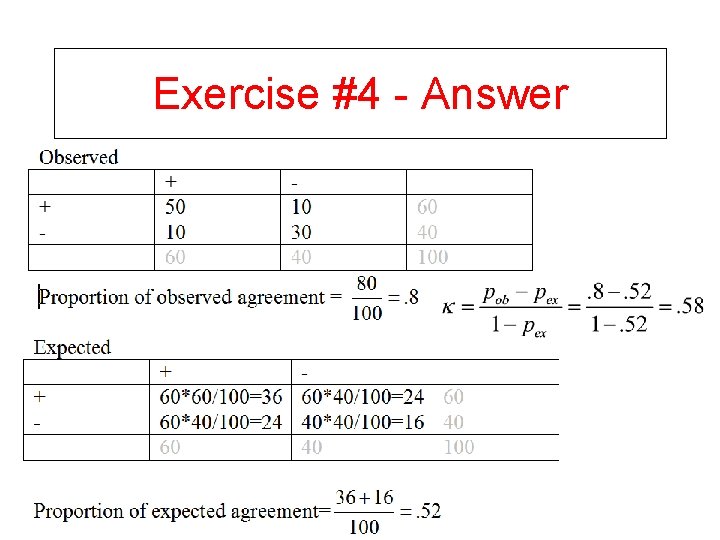
Exercise #4 - Answer

Exercise #5 • Give substantive examples of how measures of self-reported discrimination could possibly violate each of the three assumptions of classical test theory.

Exercise #5 - Answer • E(x) = 0 could be violated if the true score is underreported as a result of social desirability bias • Cov(Tx, e)=0 could be violated if people systematically overreported or underreported discrimination at either high or low extremes of the measure • Cov(ei, ej)=0 could be violated if discrimination was clustered within certain areas of a location, and multiple locations were included in the analysis pool.