Measurement of nuclear radius Four methods outlined for

Measurement of nuclear radius • Four methods outlined for charge matter radius: – Diffraction scattering – Atomic x-rays – Muonic x-rays – Mirror Nuclides

Measurement of nuclear radius • Three methods outlined for nuclear matter radius: – Rutherford scattering – Alpha particle decay – -mesic x-rays

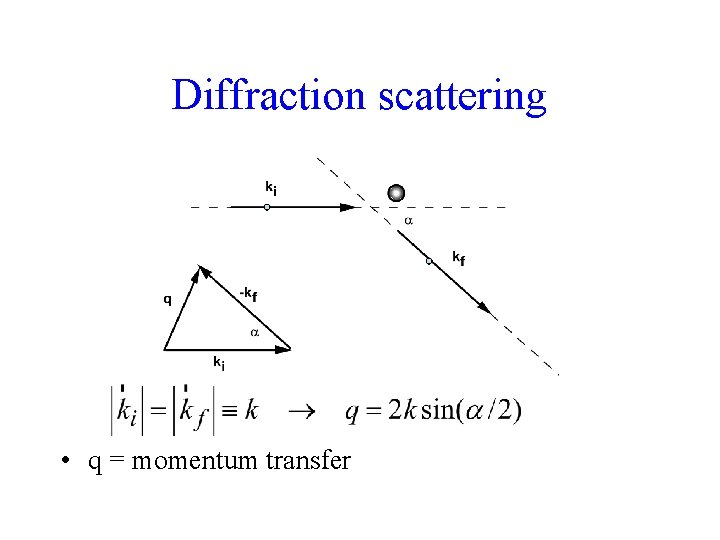
Diffraction scattering • q = momentum transfer

Diffraction scattering • Measure the scattering intensity as a function of to infer the distribution of charge in the nucleus,

Diffraction scattering • Measure the scattering intensity as a function of to infer the distribution of charge in the nucleus • • is the inverse Fourier transform of is known as the form factor for the scattering. • c. f. Figure 3. 4; what is learned from this?

Diffraction scattering • Density of electric charge in the nucleus is ≈ constant

Diffraction scattering • The charge distribution does not have a sharp boundary – Edge of nucleus is diffuse - “skin” – Depth of the skin ≈ 2. 3 f – RMS radius is calculated from the charge distribution and, neglecting the skin, it is easy to show

Atomic X-rays • Assume the nucleus is uniform charged sphere. • Potential V is obtained in two regions: – Inside the sphere – Outside the sphere

Atomic X-rays • For an electron in a given state, its energy depends on - • Assume does not change appreciably if Vpt Vsphere • Then, E = Esphere - Ept • Assume can be giving (3. 12)

Atomic X-rays • E between sphere and point nucleus for • • Compare this E to measurement and we have R. Problem! We will need two measurements to get R -Consider a 2 p 1 s transition for (Z, A) and (Z, A’) where A’ = (A-1) or (A+1) ; what x-ray does this give?

Atomic X-rays • Assume that the first term will be ≈ 0. Why? • Then, use E 1 s from (3. 13) for each E 1 s term. Why?

Atomic X-rays • This x-ray energy difference is called the “isotope shift” • We assumed that R = Ro A 1/3. Is there any authentication? • How good does your spectrometer have to be to see the effect? • We assumed we could use hydrogen-line 1 s wavefunctions Are these good enough to get good results? • Can you use optical transitions instead of x-ray transitions?

Muonic X-rays • Compare this process with atomic (electronic) x-rays: – – • • Similarities Differences Advantages Disadvantages What is ao ? Pauli Exclusion principle for muons, electrons?

Coulomb Energy Differences • Calaulate the Coulomb energy of the charge distribution directly Consider mirror nuclides: Measure EC; How? Assume R is same for both nuclides. Why?

Measurement of nuclear radius • Three methods outlined for nuclear matter radius: – Rutherford scattering – Alpha particle decay – -mesic x-rays