Measurement Note 1 Measurement Systems In NZ the

Measurement

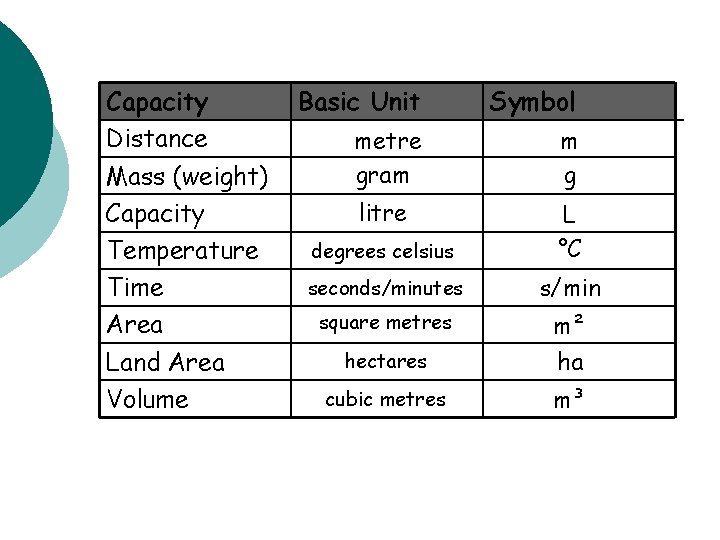
Note 1 : Measurement Systems In NZ the measurement system used is the metric system. The units relate directly to each other.

Capacity Distance Mass (weight) Capacity Temperature Time Area Land Area Volume Basic Unit Symbol metre gram m g litre degrees celsius L °C seconds/minutes s/min square metres hectares m² ha cubic metres m³

To change within a unit from one prefix to another prefix, we either multiply or divide by a power of 10. smaller to larger unit divide by a power of 10 larger to smaller unit multiply by a power of 10 Examples: convert the following 5. 76 m to cm 489 m. L to L 3789600 cm to km

Homework Book Page 159 -160

STARTERS Convert the following: 59 m. L to L 4200 kg to tonne 11 m 465 mm to cm A dairy stores milk in 5 litre containers. How many 350 m. L milkshakes can be made from one of these containers?

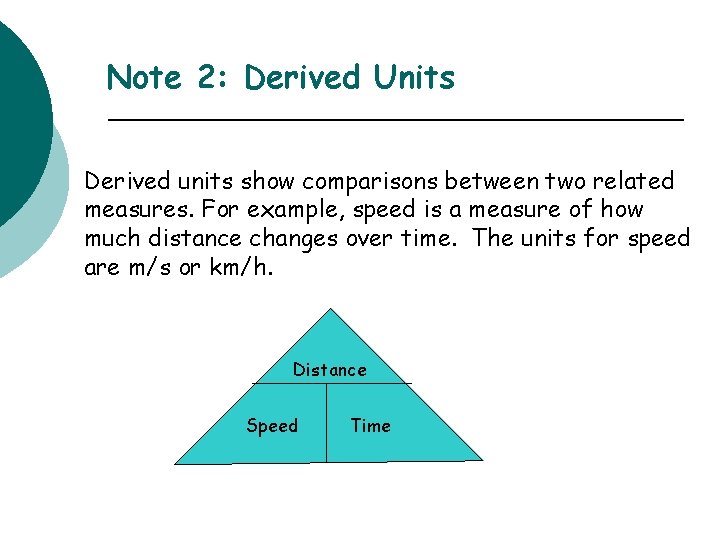
Note 2: Derived Units Derived units show comparisons between two related measures. For example, speed is a measure of how much distance changes over time. The units for speed are m/s or km/h. Distance Speed Time

Examples: A cyclist travels at a steady speed of 24 km/h for 40 minutes. How far did the cyclist travel? 40 minutes = 2/3 hour Distance = speed x time = 24 x 2/3 = 16 km

Changing from one speed unit to another Note: 1 km = 1000 m 1 hour = 3600 sec Examples: Change 45 km/h into m/s 45 km/h = 45 x 1000 m/h = 45000 m/3600 s = 12. 5 m/s

Examples: Change 74 m/s into km/h 74 m/s = 3600 x 74 m/h = 266400 m/h = 266. 4 km/h

Homework Book Page 162 -163

STARTERS Convert the following: 19 m/s to km/h A truck travels at an average speed of 75 km/h for a distance of 300 km. What time does the journey take? A Boeing 747 has a cruising speed of 910 km/h. Change this into m/s?

Note 3: Perimeter The perimeter is the distance around the outside of a shape. Start at one corner and work around the shape calculating any missing sides. 5 cm 6 cm 2 cm Perimeter = 5 cm + 3 cm + 6 cm + 2 cm + 11 cm + 5 cm = 32 cm

Homework Book Page 164 - 166

STARTERS Calculate the perimeter of The plan shows an L-shaped paddock. Calculate the total cost of fencing it at $24/m

Note 4: Circumference The perimeter of a circle is called the circumference. The formula for the circumference is: C = πd or C = 2πr where d = diameter r = radius. Example: Find the circumference of C = 2πr = 2 x π x 8 cm = 50. 3 cm (1 dp)

If a sector has an angle at the centre equal to x, then the arc length is x/360 of the circumference. Example: Find the perimeter of the sector Angle of sector = 360° - 120 ° = 240 ° Arc Length = x/360 x 2πr = 240/360 x 2 x π x 6 m = 25. 1 m (1 dp) Perimeter = 2 x 6 m + 25. 1 m = 37. 1 m

Homework Book Page 167 - 169

STARTERS Calculate the perimeter of Paul goes for a short cycle ride. Each wheel on his bike has a radius of 27 cm. His distance counter tells him the wheel has rotated 650 times. Find how far he has travelled in metres.

Note 5: Area is measured in square units.

Examples converting units:

Examples of converting units 5. 6 cm 2 to mm 2 Big Small x 5. 6 cm 2 = 5. 6 x 100 = 560 mm 2 396000 cm 2 to m 2 Small Big ÷ 396000 cm 2 = 396000÷ 10000 = 39. 6 m 2

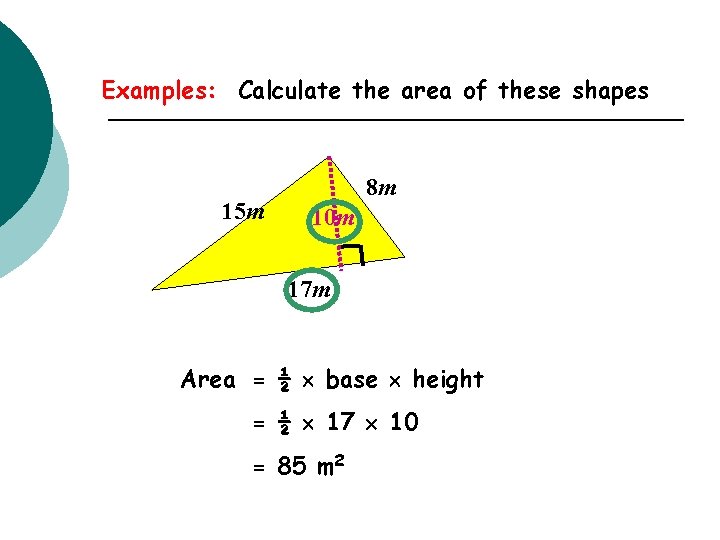
Examples: Calculate the area of these shapes 8 m 15 m 10 m 17 m Area = ½ base 7 m height 9 m = ½ 17 10 = 85 m 2 17 m 12 m ½ 12 7 = 42 m 2

Radius = 7 ÷ 2 = 3. 5 cm Area = x/360 x π x r² = 180/360 x π x 3. 5² = 19. 2 m² (1 dp) Area = ½ (sum of bases) x height = ½(9 + 12) x 7 = 73. 5 m² (1 dp)

Homework Book Page 170 – 171

STARTERS Find the area of A chocolate bar is wrapped in a rectangular piece of foil measuring 10 cm by 15 cm. Calculate the area of the piece of foil. How many pieces could be cut out from a larger sheet of foil measuring 120 cm by 75 cm?

Note 6: Compound Area v Compound shapes are made up of more than one mathematical shape. v To find the area of a compound shape, find the areas of each individual shapes and either add or subtract as you need to.

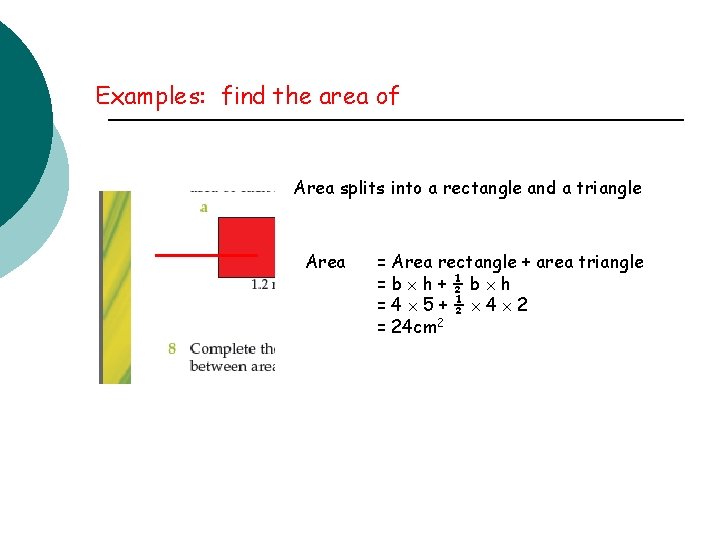
Examples: find the area of Area splits into a rectangle and a triangle Area = Area rectangle + area triangle =b h+½b h =4 5+½ 4 2 = 24 cm 2

Area splits into a rectangle with another rectangle taken away Area = area big rectangle – area small rectangle =b h-b h =6 4– 3 2 = 18 m 2

Homework Book Page 172 – 174

STARTERS Find the area of Trapezium = 750 Rectangle = 1000 Half Circle = 628. 3 Area = 750 + 1000 - 628. 3 = 1121. 7 cm 2

Note 7: Finding missing parts of shapes To find missing sides of shapes, rearrange the formulas. Example 1: The area of the triangle is 135 m 2. Calculate the height of the triangle. Area = ½ base height 135 = ½ 18 x 135 = 9 x x = 15 m

Example 2: Calculate the radius of a circle with an area of 65 cm 2. Area = π r 2 65 = π r 2 = 65/π r = √ 65/π = 4. 5 cm

EXERCISES: Each of these shapes has an area of 60 cm 2. Calculate the lengths marked x. 10 cm 15 cm 2. 5 cm √ 60 =7. 7 cm

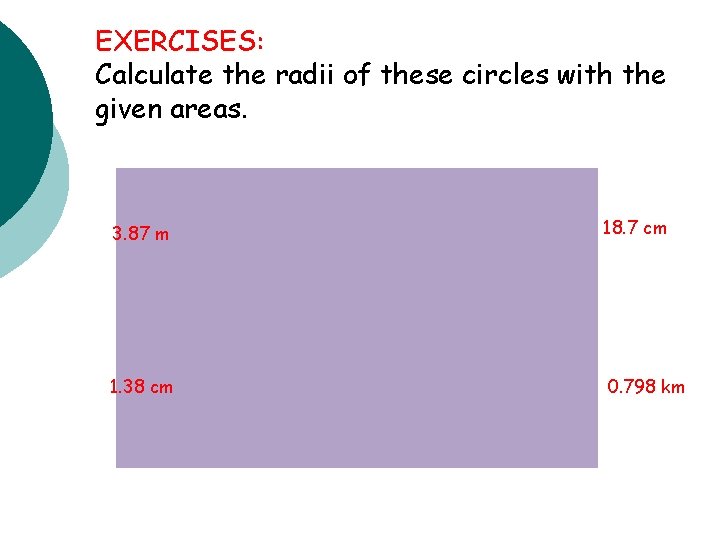
EXERCISES: Calculate the radii of these circles with the given areas. 3. 87 m 18. 7 cm 1. 38 cm 0. 798 km

EXERCISES: A circle has an area of 39. 47 m 2. Calculate: q Radius q Diameter 3. 55 m 7. 09 m q circumference 22. 27 m

STARTERS Calculate the length if the area is 60 cm 2 A rotating irrigation jet waters an area of 2600 m 2. If you did not want to get wet, how far would you have to stand from the jet? (to the nearest metre)

Note 8: Surface Area The surface area of a solid is the sum of the areas of all its faces. Example 1: Calculate the surface area of this triangular prism The prism has 5 faces Ø 2 triangles Ø 3 rectangles

Example 1: Calculate the surface area of this triangular prism Front triangle = ½ x 6 x 8 = 24 cm 2 Back triangle = ½ x 6 x 8 = 24 cm 2 Left rectangle = 10 x 12 = 120 cm 2 Bottom rectangle = 6 x 12 = 72 cm 2 Right rectangle = 8 x 12 = 96 cm 2 Total surface area = 24 + 120 + 72 + 96 = 336 cm 2

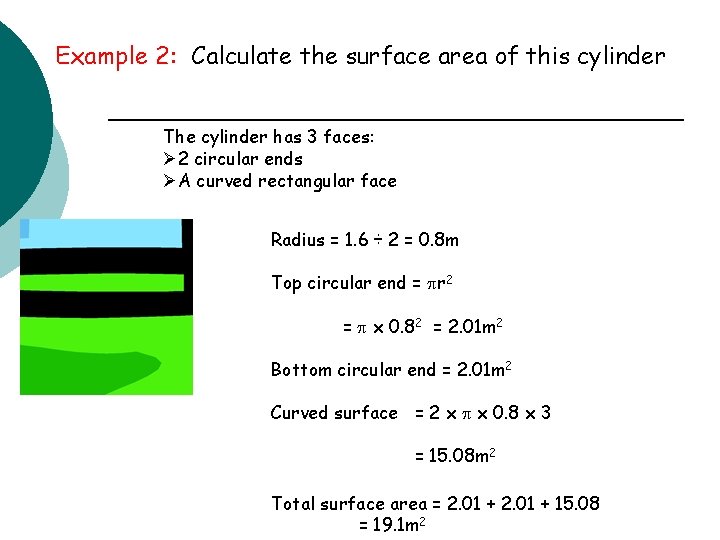
Example 2: Calculate the surface area of this cylinder The cylinder has 3 faces: Ø 2 circular ends ØA curved rectangular face Radius = 1. 6 ÷ 2 = 0. 8 m Top circular end = r 2 = x 0. 82 = 2. 01 m 2 Bottom circular end = 2. 01 m 2 Curved surface = 2 x x 0. 8 x 3 = 15. 08 m 2 Total surface area = 2. 01 + 15. 08 = 19. 1 m 2

The formula for the surface area of a sphere is: SA = 4 r 2 Example 3: Calculate the surface area of this sphere SA = 4 r 2 = 4 x x 182 = 4071. 5 m 2

Homework Book Page 172 – 174

STARTERS Calculate the length if the area is 60 cm 2 A rotating irrigation jet waters an area of 2600 m 2. If you did not want to get wet, how far would you have to stand from the jet? (to the nearest metre)

Note 9: Volume of Prisms Volume = Area of cross section × Length Area L The volume of a solid figure is the amount of space it occupies. It is measured in cubic centimetres, cm 3 or cubic metres, m 3

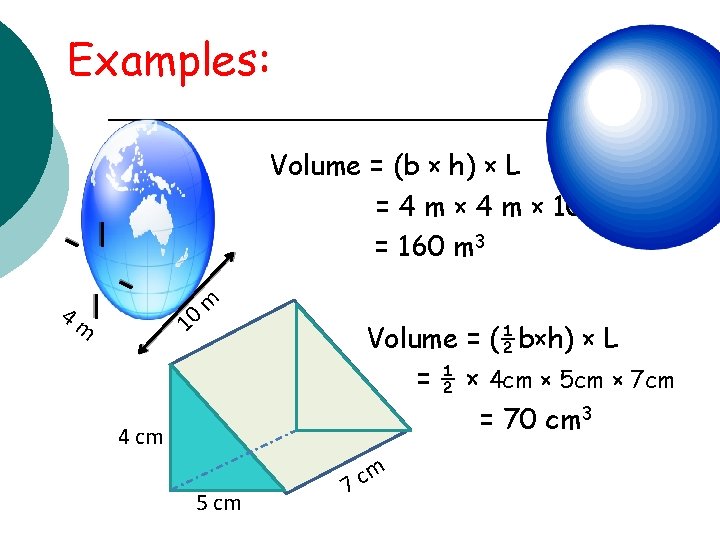
Examples: Volume = (b × h) × L = 4 m × 10 m = 160 m 3 4 m 10 m 4 cm 5 cm Volume = (½b×h) × L = ½ × 4 cm × 5 cm × 7 cm = 70 cm 3 m c 7

Cylinder – A Circular Prism Volume = Area of cross section × Length Volume (cylinder) = πr 2× h V = πr 2× h m 8 c c 1. 2 m = π(1. 2 cm)2 × 8 cm = 36. 19 cm 3 (4 sf)

Homework Book Page 172 – 174

Starter This tent-shaped plastic hothouse is to change its air five times every hour. What volume of air per minute is required from the fan to achieve this? Round appropriately. Volume = ½ × 13 × 12 × 8 = 624 m 3 12 m m 0. 8 624 m 3 × 5 = 3120 m 3/hr 13 m = 52 m 3/min

Note 10: Volume of Pyramids, cones & Spheres V = 1/ 3 A × h A = area of base h = perpendicular height Apex V = 1/ 3 A × h = 1/3 (5 m× 4 m)× 8 m 5 m 4 m = 53. 3 m 3

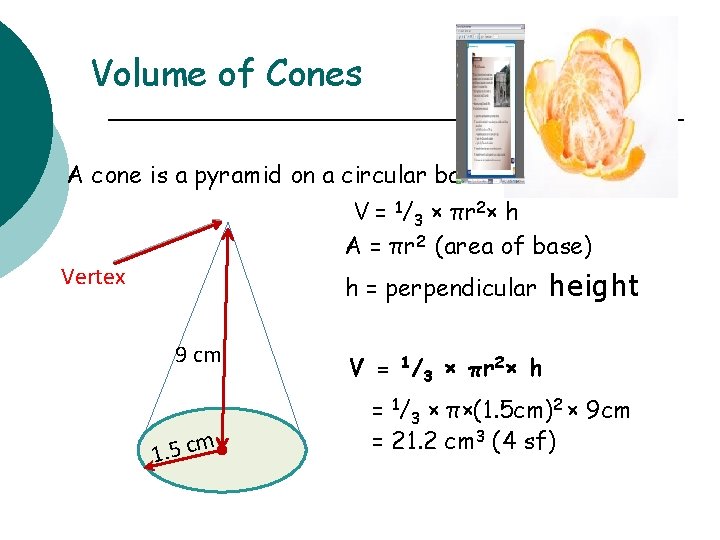
Volume of Cones A cone is a pyramid on a circular base V = 1/3 × πr 2× h A = πr 2 (area of base) Vertex h = perpendicular 9 cm 1. 5 cm height V = 1/3 × πr 2× h = 1/3 × π×(1. 5 cm)2 × 9 cm = 21. 2 cm 3 (4 sf)

Spheres A sphere is a perfectly round ball. It has only one measurement: the radius, r. The volume of a sphere is: V = 4/3πr 3

Example 1: Calculate the volume of the pyramid below V = 1/ 3 A x h = 1/3 x 5 m x 4 m x 6 m = 40 m 3

Example 2: Calculate the volume of a football with a diameter of 23 cm V = 4/3πr 3 Radius = 23 ÷ 2 = 11. 5 cm V = 4/3 × π(11. 5 cm)3 = 6371 cm 3

Homework Book Page 182

Starter mm. Vwith peel = 4/3 π (45)3 = 381 704 mm 3 Vno peel = 4/3 π (40)3 = 268 083 mm 3 Vpeel = Vwith peel – Vno peel = 113 621 mm 3 = 114 000 mm 3

Note 11: Compound Volume Divide compound solids into solids, such as, prisms and cylinders and add or subtract as for area compounds.

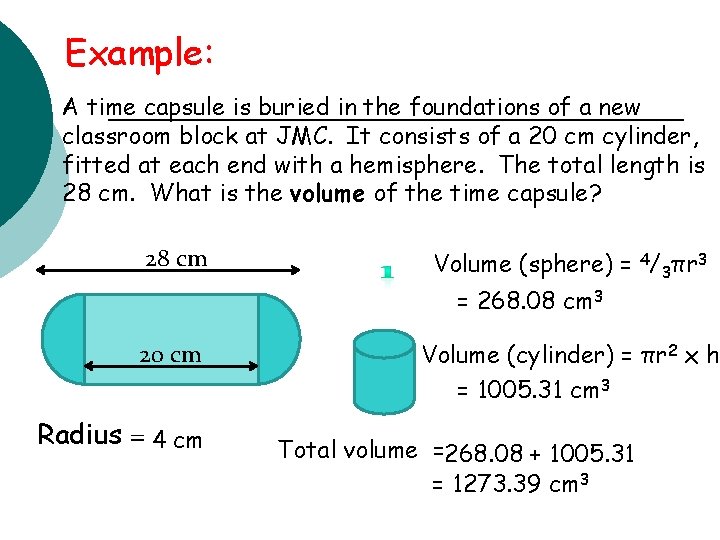
Example: A time capsule is buried in the foundations of a new classroom block at JMC. It consists of a 20 cm cylinder, fitted at each end with a hemisphere. The total length is 28 cm. What is the volume of the time capsule? 28 cm Volume (sphere) = 4/3πr 3 = 268. 08 cm 3 20 cm Radius = 4 cm Volume (cylinder) = πr 2 x h = 1005. 31 cm 3 Total volume =268. 08 + 1005. 31 = 1273. 39 cm 3

Homework Book Page 183

Starter A gold wedding band with diameter 16 mm & a cross section as shown below shows the band is semi circular with a radius of 4 mm. Estimate the volume by imagining the ring cut and opened up. Density of gold is 19. 3 g/cm 3 16 mm Estimate the value of the ring 4 mm if it was melted down and recovered. Assume gold is Mass = 1. 263 cm 3 × 19. 3 g/cm 3 currently traded for $59. 70/g = 24. 38 cm 3 Length of ‘opened up’ ring = π × 1. 6 cm = 5. 0265 cm Value = 24. 38 g x $59. 70 = $1456 Volume of ‘opened up’ ring = ½ × π × 0. 42 × 5. 0265 cm = 1. 263 cm 3

Note 12: Liquid Volume (Capacity) There are 2 ways in which we measure volume: ¡ Solid shapes have volume measured in cubic units (cm 3, m 3 …) ¡ Liquids have volume measured in litres or millilitres (m. L) Metric system – Weight/volume conversions for water. Weight Liquid Volume Equivalent Solid Volume 1 gram 1 m. L 1 cm 3 1 kg 1 litre 1000 cm 3

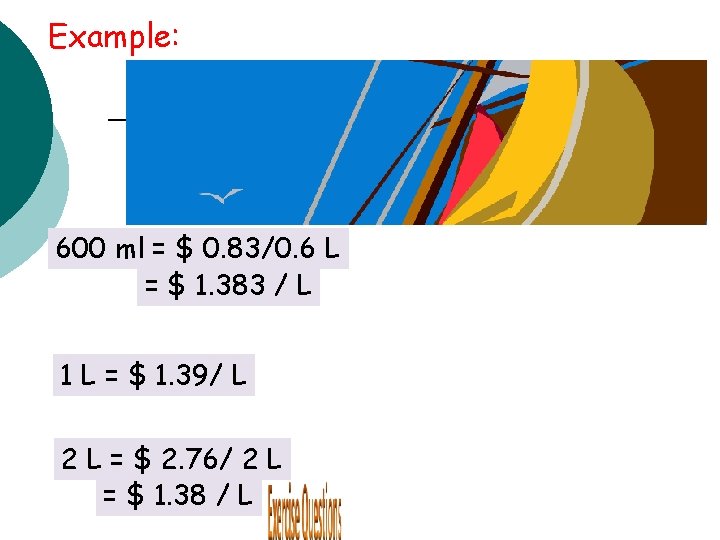
Example: 600 ml = $ 0. 83/0. 6 L = $ 1. 383 / L 1 L = $ 1. 39/ L 2 L = $ 2. 76/ 2 L = $ 1. 38 / L

Example Calculate the area of glass required for the fish tank 7122 cm 2 S. A. = 2(55 × 42) + 2(18 × 42) + (55 x=18) Calculate the volume of water in the tank. Give your answer to the nearest litre Vtank = 55 × 42 × 18 = 41580 cm 3 Vwater = 4/5 (41580) = 33264 cm 3 42 cm = 33 L 55 cm

Homework Book Page 185

Starter Calculate the area of glass required for the fish tank 7122 cm 2 S. A. = 2(55 × 42) + 2(18 × 42) + (55 x=18) Calculate the volume of water in the tank. Give your answer to the nearest litre Vtank = 55 × 42 × 18 = 41580 cm 3 Vwater = 4/5 x 41580 = 33264 cm 3 42 cm = 33 L 55 cm

Note 13: Time ¡ Equivalent times (in seconds) 1 minute = 60 seconds 1 hour = 60 mins = 60 x 60 secs = 3600 seconds 1 day = 24 hours = 24 x 60 seconds = 86 400 seconds 24 hour time is represented using 4 digits 0630 hours 12 hour clock times are followed by am or pm 6: 30 am

Example: If I arrive at school at 8: 23 am and leave at 4: 15 pm. How long in hours and minutes do I spend at school? Hours Minutes 8: 23 am - 12 3 37 12 - 4: 15 pm 4 15 Total time 7 52

Homework Book Page 185

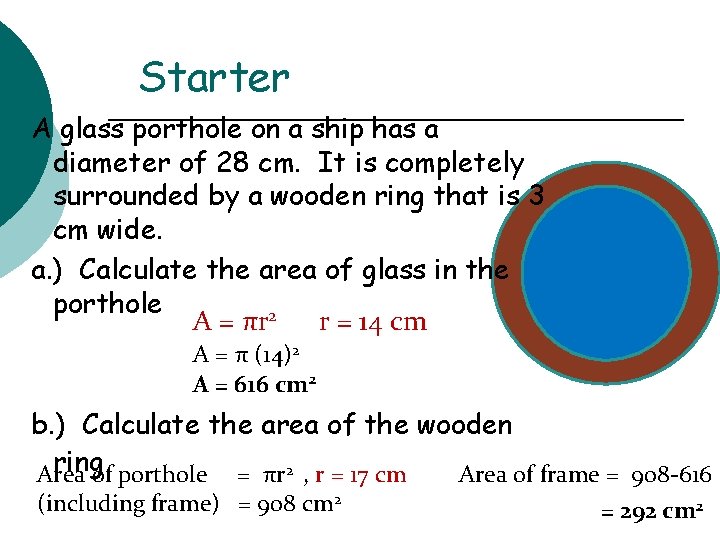
Starter A glass porthole on a ship has a diameter of 28 cm. It is completely surrounded by a wooden ring that is 3 cm wide. a. ) Calculate the area of glass in the porthole A = πr 2 r = 14 cm A = π (14)2 A = 616 cm 2 b. ) Calculate the area of the wooden ringof porthole = πr 2 , r = 17 cm Area of frame = 908 -616 (including frame) = 908 cm 2 = 292 cm 2

Note 14: Limits of Accuracy Measurements are never exact. There is a limit to the accuracy with which a measurement can be made. The limits of accuracy of measurement refers to the range of values within which the true value of the measurement lies. The range of values is defined by an upper limit and a lower limit.

To find the upper limit, add 5 to the nearest significant place. ¡ To find the lower limit, minus 5 to the nearest significant place. ¡ Example 1: The distance to Bluff on a signpost reads 17 km. The upper limit is 17 + 0. 5 = The lower limit is 17 – 0. 5 = 17. 5 km 16. 5 km Therefore the limits of accuracy are 16. 5 km ≤ Bluff < 17. 5 km

Example 2: At the Otago vs Canterbury game at the stadium it was reported that 23500 people attended. Give the limits of accuracy for the number of people attending the game? The upper limit is 23500 + 50 = 23550 The lower limit is 23500 – 50 = 23450 Therefore the limits of accuracy are: 23450 ≤ People < 23550

Give the limits of measurements: 1. ) 68 mm 2. ) 397 mm 3. ) 4 seconds 4. ) 50 g 5. ) 5890 kg 6. ) 820 cm 7. ) 92 kg 8. ) 89. 1° accuracy for these 67. 5 mm ≤ x ≤ 68. 5 mm 396. 5 mm ≤ x ≤ 397. 5 mm 3. 5 seconds ≤ x ≤ 4. 5 seconds 45 g ≤ x ≤ 55 g 5885 kg ≤ x ≤ 5895 kg 815 cm ≤ x ≤ 825 cm 91. 5 kg ≤ x ≤ 92. 5 kg 89. 05° ≤ x ≤ 89. 15°